Abstract
A topological meron features a non-coplanar structure, whose order parameters in the core region are perpendicular to those near the perimeter. A meron is half of a skyrmion, and both have potential applications for information carrying and storage. Although merons and skyrmions in ferromagnetic materials can be readily obtained via inter-spin interactions, their behaviour and even existence in ferroelectric materials are still elusive. Here we observe using electron microscopy not only the atomic morphology of merons with a topological charge of 1/2, but also a periodic meron lattice in ultrathin PbTiO3 films under tensile epitaxial strain on a SmScO3 substrate. Phase-field simulations rationalize the formation of merons for which an epitaxial strain, as a single alterable parameter, plays a critical role in the coupling of lattice and charge. This study suggests that by engineering strain at the nanoscale it should be possible to fabricate topological polar textures, which in turn could facilitate the development of nanoscale ferroelectric devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Zubko, P., Gariglio, S., Gabay, M., Ghosez, P. & Triscone, J.-M. Interface physics in complex oxide heterostructures. Annu. Rev. Condens. Matter Phys. 2, 141–165 (2011).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Tang, Y. L. et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO3 films. Science 348, 547–551 (2015).
Yadav, A. K. et al. Observation of polar vortices in oxide superlattices. Nature 530, 198–201 (2016).
Lin, S.-Z. et al. Topological defects as relics of emergent continuous symmetry and Higgs condensation of disorder in ferroelectrics. Nat. Phys. 10, 970–977 (2014).
Tom, K. & Ajit, S. Condensed matter analogues of cosmology. J. Phys. Condens. Matter 25, 400301 (2013).
Seidel, J., Vasudevan, R. K. & Valanoor, N. Topological structures in multiferroics - domain walls, skyrmions and vortices. Adv. Electron. Mater. 2, 1500292 (2016).
Roszler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797–801 (2006).
Muehlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).
Wachowiak, A. et al. Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002).
Phatak, C., Petford-Long, A. K. & Heinonen, O. Direct observation of unconventional topological spin structure in coupled magnetic discs. Phys. Rev. Lett. 108, 067205 (2012).
Wintz, S. et al. Topology and origin of effective spin meron pairs in ferromagnetic multilayer elements. Phys. Rev. Lett. 110, 177201 (2013).
Siracusano, G. et al. Magnetic radial vortex stabilization and efficient manipulation driven by the Dzyaloshinskii–Moriya interaction and spin-transfer torque. Phys. Rev. Lett. 117, 087204 (2016).
Tan, A. et al. Topology of spin meron pairs in coupled Ni/Fe/Co/Cu(001) disks. Phys. Rev. B 94, 014433 (2016).
Yu, X. Z. et al. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 564, 95–98 (2018).
Jia, C. L., Urban, K. W., Alexe, M., Hesse, D. & Vrejoiu, I. Direct observation of continuous electric dipole rotation in flux-closure domains in ferroelectric Pb(Zr,Ti)O3. Science 331, 1420–1423 (2011).
Li, S. et al. Periodic arrays of flux-closure domains in ferroelectric thin films with oxide electrodes. Appl. Phys. Lett. 111, 052901 (2017).
Liu, Y. et al. Large scale two-dimensional flux-closure domain arrays in oxide multilayers and their controlled growth. Nano Lett. 17, 7258–7266 (2017).
Nelson, C. T. et al. Spontaneous vortex nanodomain arrays at ferroelectric heterointerfaces. Nano Lett. 11, 828–834 (2011).
Zhang, Q. et al. Nanoscale bubble domains and topological transitions in ultrathin ferroelectric films. Adv. Mater. 29, 1702375 (2017).
Lu, L. et al. Topological defects with distinct dipole configurations in PbTiO3/SrTiO3 multilayer films. Phys. Rev. Lett. 120, 177601 (2018).
Li, L. Z. et al. Defect-induced hedgehog polarization states in multiferroics. Phys. Rev. Lett. 120, 137602 (2018).
Naumov, I., Bellaiche, L. & Fu, H. X. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 432, 737–740 (2004).
Rodriguez, B. J. et al. Vortex polarization states in nanoscale ferroelectric arrays. Nano Lett. 9, 1127–1131 (2009).
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Li, Y. L., Hu, S. Y., Liu, Z. K. & Chen, L. Q. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films. Acta Mater. 50, 395–411 (2002).
Damodaran, A. R. et al. Three-state ferroelastic switching and large electromechanical responses in PbTiO3 thin films. Adv. Mater. 29, 1702069 (2017).
Glazer, A. M. & Mabud, S. A. Powder profile refinement of lead zirconate titanate at several temperatures. II. Pure PbTiO3. Acta Crystallogr. B B34, 1065–1070 (1978).
Pennycook, S. J. & Jesson, D. E. High-resolution Z-contrast imaging of crystals. Ultramicroscopy 37, 14–38 (1991).
Uecker, R. et al. Properties of rare-earth scandate single crystals (Re=Nd−Dy). J. Cryst. Growth 310, 2649–2658 (2008).
Gesing, T. M., Uecker, R. & Buhl, J. C. Refinement of the crystal structure of praseodymium orthoscandate, PrScO3. Z. Kristallogr. New Cryst. Struct. 224, 365–366 (2009).
Fong, D. D. et al. Stabilization of monodomain polarization in ultrathin PbTiO3 films. Phys. Rev. Lett. 96, 127601 (2006).
Xie, L. et al. Giant ferroelectric polarization in ultrathin ferroelectrics via boundary-condition engineering. Adv. Mater. 29, 1701475 (2017).
Anthony, S. M. & Granick, S. Image analysis with rapid and accurate two-dimensional Gaussian fitting. Langmuir 25, 8152–8160 (2009).
Jia, C. L. et al. Atomic-scale study of electric dipoles near charged and uncharged domain walls in ferroelectric films. Nat. Mater. 7, 57–61 (2008).
Hytch, M. J., Snoeck, E. & Kilaas, R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy 74, 131–146 (1998).
Hytch, M. J., Putaux, J. L. & Penisson, J. M. Measurement of the displacement field of dislocations to 0.03 Å by electron microscopy. Nature 423, 270–273 (2003).
Tang, Y. L., Zhu, Y. L. & Ma, X. L. On the benefit of aberration-corrected HAADF-STEM for strain determination and its application to tailoring ferroelectric domain patterns. Ultramicroscopy 160, 57–63 (2016).
Li, Y. L., Hu, S. Y., Liu, Z. K. & Chen, L. Q. Effect of electrical boundary conditions on ferroelectric domain structures in thin films. Appl. Phys. Lett. 81, 427–429 (2002).
Hong, L., Soh, A. K., Song, Y. C. & Lim, L. C. Interface and surface effects on ferroelectric nano-thin films. Acta Mater. 56, 2966–2974 (2008).
Acknowledgements
We are grateful to D. S. Ma, at Nankai University (now at Cornell University), for participation in film growth by PLD and TEM specimen preparation, and C. J. Li at Shenyang National Laboratory for Materials Science for experimental assistance with XRD and RSM. This work is supported by the Key Research Program of Frontier Sciences CAS (QYZDJ-SSW-JSC010), the National Natural Science Foundation of China (no. 51671194, no. 51971223, no. 51922100) and Shenyang National Laboratory for Materials Science (L2019R06, L2019R08, L2019F01, L2019F13). Y.L.T. acknowledges the Youth Innovation Promotion Association CAS (no. 2016177).
Author information
Authors and Affiliations
Contributions
X.L.M. and Y.L.Z. conceived the project on the architecture of quantum materials modulated by ferroelectric polarizations; Y.L.Z., X.L.M., Y.P.F. and Y.L.T. designed the sample structure and subsequent experiments. Y.P.F. performed the thin-film growth and STEM observations. Y.J.W. and X.W.G. performed phase-field simulations and Y.J.W. carried out digital analysis of the STEM data; L.X.Y., M.J.Z., W.R.G. and M.J.H. participated in the thin-film growth and STEM observations; B.W. contributed technical support on the Titan platform of the G2 60–300-kV aberration-corrected STEM. All authors participated in discussion and interpretation of the data.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 The in-plane strain and lattice rotation of polar convergent meron in the PTO/SSO film.
(a) The atomic-resolved cross-sectional HAADF-STEM image of the trapezoidal domain. Yellow and red circles denote the Pb and Ti atom columns, respectively. Yellow arrows denote the directions of −δTi vectors. (b) The 2D mapping of the in-plane strain (εxx). (c) The 2D mapping of the lattice rotation (Rx).
Extended Data Fig. 2 The statistical spaces of two adjacent convergent merons at the direction along stripe domain walls.
Note the most probable space is about 8 nm.
Extended Data Fig. 3 Reversed Ti-displacement vector map based on atomic-resolved planar-view HAADF-STEM images of stripe domains, showing the divergent meron arrays (black dashed circles) at “tail-to-tail” domain walls (black dashed lines).
The inset is a magnified polarization map of the divergent meron corresponding to the area labeled as “1”.
Extended Data Fig. 4 Observation of antimerons in PTO/SSO films.
(a) Reversed Ti-displacement vector map, showing the relationship between convergent merons, divergent merons and antimerons. (b) and (c) The polarization maps of two antimerons corresponding to the areas labeled as “1-2” in (a).
Extended Data Fig. 5 The structure and topological density of a meron-antimeron combination (MAC).
(a) The 3D domain structure of a 5 nm film. (b) and (c) Vertical cross sections corresponding to black boxes in a. A convergent IP polarization distribution is found in b and the ordinary a/c domain is found in c. (d and e) The horizontal cross-sectional slice (marked by black boxes in a) and the zoom-in images. (f) The corresponding topological density distribution. (g) The schematic diagram of the process of a meron and an antimeron to form a MAC. The bars in these figures indicate 2 nm, except that in (d). The topological density is expressed as a value per square nanometre.
Extended Data Fig. 6 The topological protection of merons and antimerons.
(a) The classification of merons (M), antimerons (A) and MACs according to their topological charges and volumes. (b) The relationship between the coercive field and the volume of the central c domain for merons (M), antimerons (A) and MACs. It is clear that the coercive fields of merons and antimerons are generally larger than those of MACs.
Extended Data Fig. 7 The comparison of energy densities for the lattice and random meron models.
(a-c) The Pz component, the bulk energy density and the elastic energy density of the lattice model. (d-f) Those quantities of the random model.
Extended Data Fig. 8 The domain configuration in a 5 nm thick PTO/DSO film.
(a) A cross-sectional low-magnification HAADF-STEM image viewed along the [100] direction of PTO. (b) GPA of (a) reveals the in-plane strain (εxx). (c) An atomic-resolution image corresponding to the white dashed rectangular box in (a). Yellow and red circles denote the Pb and Ti atom columns, respectively. Yellow arrows denote the directions of −δTi vectors. (d) The mapping of −δTi vectors, which are consistent with the spontaneous polarization directions of PTO.
Extended Data Fig. 9 The domain configuration in a 5 nm thick PTO/GSO film.
(a) A cross-sectional low-magnification HAADF-STEM image viewed along the [100] direction of PTO. (b) GPA of (a) reveals the in-plane strain (εxx). (c) and (e) The atomic-resolution images corresponding to two white dashed rectangular boxes in (a), respectively. Yellow and red circles denote the Pb and Ti atom columns, respectively. Yellow arrows denote the directions of −δTi vectors. (d) and (f) The mappings of −δTi vectors, which are consistent with the spontaneous polarization directions of PTO.
Extended Data Fig. 10 The effect of the epitaxial strain on the formation of merons and antimerons.
(a) The variation of domain structure with respective to the epitaxial strain. Only c domains exist at very small tensile strain, such as 0.6%. When the strain is 1.3% (corresponding to DSO), a/c domains emerge. When the strain is very large, such as >= 3.1% (corresponding to PSO), only a domains exist. Merons were observed at intermediated strain, such as 1.8% (corresponding to GSO) and 2.3% (corresponding to SSO). (b) and (c) The densities of merons (b) and antimerons (c) as the function of the epitaxial strain.
Supplementary information
Supplementary Information
Supplementary Notes 1–5, Supplementary Figs. 1–17 and Supplementary Tables 1–3.
Source data
Source Data Fig. 1
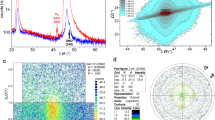
Experimental RSM data of Fig. 1b.
Source Data Fig. 2
Off-centre shift data of Ti atoms in Fig. 2b,c.
Source Data Fig. 3
Polarization vector matrix of the lattice model for Fig. 3.
Source Data Fig. 4
Polarization vector and topological density matrices of the random model for Fig. 4.
Source Data Extended Data Fig. 1
IP strain and lattice rotation data in Extended Data Fig. 1b,c.
Source Data Extended Data Fig. 2
Statistical source data of Extended Data Fig. 2.
Source Data Extended Data Fig. 3
Off-centre shift data of Ti atoms in Extended Data Fig. 3.
Source Data Extended Data Fig. 4
Off-centre shift data of Ti atoms in Extended Data Fig. 4a.
Source Data Extended Data Fig. 5
Polarization vector and topological density matrices of the random model for Extended Data Fig. 5.
Source Data Extended Data Fig. 6
Source data of Extended Data Fig. 6.
Source Data Extended Data Fig. 7
Polarization vector and energy density matrices of the lattice (Extended Data Fig. 7a–c) and random (Extended Data Fig. 7d–f) models.
Source Data Extended Data Fig. 8
Off-centre shift data of Ti atoms in Extended Data Fig. 8d.
Source Data Extended Data Fig. 9
Off-centre shift data of Ti atoms in Extended Data Fig. 9d,f.
Source Data Extended Data Fig. 10
Polarization vector matrices for Extended Data Fig. 10a (*.dat files) and the statistical densities of merons and antimerons for Extended Data Fig. 10b,c (the *.xlsx file).
Rights and permissions
About this article
Cite this article
Wang, Y.J., Feng, Y.P., Zhu, Y.L. et al. Polar meron lattice in strained oxide ferroelectrics. Nat. Mater. 19, 881–886 (2020). https://doi.org/10.1038/s41563-020-0694-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-020-0694-8
This article is cited by
-
Flexoelectricity-driven toroidal polar topology in liquid-matter helielectrics
Nature Physics (2024)
-
Giant electric field-induced second harmonic generation in polar skyrmions
Nature Communications (2024)
-
Electrically and mechanically driven rotation of polar spirals in a relaxor ferroelectric polymer
Nature Communications (2024)
-
Polar meron-antimeron networks in strained and twisted bilayers
Nature Communications (2023)
-
Ferroelectric solitons crafted in epitaxial bismuth ferrite superlattices
Nature Communications (2023)