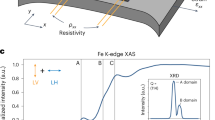
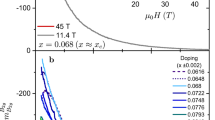
Abstract
Nematic order is the breaking of rotational symmetry in the presence of translational invariance. While originally defined in the context of liquid crystals, the concept of nematic order has arisen in crystalline matter with discrete rotational symmetry, most prominently in the tetragonal Fe-based superconductors where the parent state is four-fold symmetric. In this case the nematic director takes on only two directions, and the order parameter in such ‘Ising-nematic’ systems is a simple scalar. Here, using a spatially resolved optical polarimetry technique, we show that a qualitatively distinct nematic state arises in the triangular lattice antiferromagnet Fe1/3NbS2. The crucial difference is that the nematic order on the triangular lattice is a \(Z_3\) or three-state Potts-nematic order parameter. As a consequence, the anisotropy axes of response functions such as the resistivity tensor can be continuously reoriented by external perturbations. This discovery lays the groundwork for devices that exploit analogies with nematic liquid crystals.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).
Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Bodnar, S. Y. et al. Writing and reading antiferromagnetic Mn2Au by Néel spin-orbit torques and large anisotropic magnetoresistance. Nat. Commun. 9, 348 (2018).
Moriyama, T., Oda, K., Ohkochi, T., Kimata, M. & Ono, T. Spin torque control of antiferromagnetic moments in NiO. Sci. Rep. 8, 14167 (2018).
Saidl, V. et al. Optical determination of the Néel vector in a CuMnAs thin-film antiferromagnet. Nat. Photon 11, 91–96 (2017).
Kriegner, D. et al. Multiple-stable anisotropic magnetoresistance memory in antiferromagnetic MnTe. Nat. Commun. 7, 11623 (2016).
Kriegner, D. et al. Magnetic anisotropy in antiferromagnetic hexagonal MnTe. Phys. Rev. B 96, 214418 (2017).
Železný, J. et al. Relativistic Néel-order fields induced by electrical current in antiferromagnets. Phys. Rev. Lett. 113, 157201 (2014).
Železný, J. et al. Spin-orbit torques in locally and globally noncentrosymmetric crystals: antiferromagnets and ferromagnets. Phys. Rev. B 95, 014403 (2017).
Nair, N. L. et al. Electrical switching in a magnetically intercalated transition metal dichalcogenide. Nat. Mater. 19, 153–157 (2020).
van Laar, B., Rietveld, H. M. & Ijdo, D. J. W. Magnetic and crystallographic structures of MexNbS2 and MexTaS2. J. Solid State Chem. 3, 154–160 (1971).
Gorochov, O., Blanc-soreau, A. L., Rouxel, J., Imbert, P. & Jehanno, G. Transport properties, magnetic susceptibility and Mössbauer spectroscopy of Fe0.25NbS2 and Fe0.33NbS2. Philos. Mag. B 43, 621–634 (1981).
Yamamura, Y. et al. Heat capacity and phase transition of FexNbS2 at low temperature. J. Alloy. Compd. 383, 338–341 (2004).
Chu, J.-H. et al. In-plane resistivity anisotropy in an underdoped iron arsenide superconductor. Science 329, 824–826 (2010).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Fernandes, R. M., Orth, P. P. & Schmalian, J. Intertwined vestigial order in quantum materials: nematicity and beyond. Annu. Rev. Condens. Matter Phys. 10, 133–154 (2019).
Hecker, M. & Schmalian, J. Vestigial nematic order and superconductivity in the doped topological insulator CuxBi2Se3. npj Quantum Mater. 3, 26 (2018).
Fan, S. et al. Electronic chirality in the metallic ferromagnet Fe1/3TaS2. Phys. Rev. B 96, 205119 (2017).
Wannier, G. H. Antiferromagnetism. Triangular Ising Net. Phys. Rev. 79, 357–364 (1950).
Korshunov, S. E. Nature of phase transitions in the striped phase of a triangular-lattice Ising antiferromagnet. Phys. Rev. B 72, 144417 (2005).
Smerald, A., Korshunov, S. & Mila, F. Topological aspects of symmetry breaking in triangular-lattice ising antiferromagnets. Phys. Rev. Lett. 116, 197201 (2016).
Friend, R. H., Beal, A. R. & Yoffe, A. D. Electrical and magnetic properties of some first row transition metal intercalates of niobium disulphide. Philos. Mag. A 35, 1269–1287 (1977).
Parkin, S. S. P. & Friend, R. H. 3d transition-metal intercalates of the niobium and tantalum dichalcogenides. I. Magnetic properties. Philos. Mag. B 41, 65–93 (1980).
Horibe, Y. et al. Color theorems, chiral domain topology, and magnetic properties of Fe(x)TaS2. J. Am. Chem. Soc. 136, 8368–8373 (2014).
Doyle, S. et al. Tunable giant exchange bias in an intercalated transition metal dichalcogenide. Preprint at: https://arxiv.org/abs/1904.05872 (2019).
Straley, J. P. & Fisher, M. E. Three-state Potts model and anomalous tricritical points. J. Phys. A 6, 1310–1326 (1973).
Simpson, A. M. & Wolfs, W. Thermal expansion and piezoelectric response of PZT Channel 5800 for use in low‐temperature scanning tunneling microscope designs. Rev. Sci. Instrum. 58, 2193–2195 (1987).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Hicks, C. W., Barber, M. E., Edkins, S. D., Brodsky, D. O. & Mackenzie, A. P. Piezoelectric-based apparatus for strain tuning. Rev. Sci. Instrum. 85, 065003 (2014).
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153–178 (2010).
Sapozhnik, A. A. et al. Direct imaging of antiferromagnetic domains in Mn2Au manipulated by high magnetic fields. Phys. Rev. B 97, 134429 (2018).
Bodnar, S. Y. et al. Imaging of current induced Néel vector switching in antiferromagnetic Mn2Au. Phys. Rev. B 99, 140409 (2019).
Acknowledgements
We thank D. H. Lee and J. E. Moore for useful discussions and N. Tamura for support at the Advanced Light Source. Optical measurements were performed at the Lawrence Berkeley National Laboratory in the Quantum Materials programme supported by the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the US Department of Energy under contract no. DE-AC02- 05CH11231. A.L. and J.O. received support for optical measurements from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant no. GBMF4537 to J.O. at University of California, Berkeley. Work by J.G.A., E.M., C.J. and S.D. was supported as part of the Center for Novel Pathways to Quantum Coherence in Materials, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences. Synthesis of Fe1/3NbS2 was supported by Laboratory Directed Research and Development Program of Lawrence Berkeley National Laboratory under contract no. DE-AC02-05CH11231. J.G.A. and N.L.N. received support from the Gordon and Betty Moore Foundation’s EPiQS Initiative grant no. GBMF9067 to J.G.A. at University of California, Berkeley. R.M.F. was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, under award DE-SC0012336 and, during completion of the work, under award DE‐SC0020045. X-ray diffraction to register crystal orientation was carried out at beamline 12.3.2 at the Advanced Light Source, which is a Department of Energy User Facility, under contract no. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
A.L. and C.L. performed and contributed equally to the birefringence microscopy measurements and data analysis. C.J., S.D. and E.M. grew and characterized the crystals. E.M., N.L.N. and J.G.A. discovered the switching effect that motivated this project. J.W.F.V. and R.M.F. developed the theoretical model. W.C. performed the simulation of depth profiling. D.R. assisted with optical measurements. J.O., A.L., C.L., J.W.F.V. and R.M.F. wrote the manuscript. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–7.
Source data
Source Data Fig. 1
Source data for Fig. 1b,c
Source Data Fig. 2
Source data for Fig. 2a,b,c
Source Data Fig. 3
Source data for Fig. 3a,b
Source Data Fig. 5
Source data for Fig. 5b,c,e,f
Rights and permissions
About this article
Cite this article
Little, A., Lee, C., John, C. et al. Three-state nematicity in the triangular lattice antiferromagnet Fe1/3NbS2. Nat. Mater. 19, 1062–1067 (2020). https://doi.org/10.1038/s41563-020-0681-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-020-0681-0
This article is cited by
-
Long-range, non-local switching of spin textures in a frustrated antiferromagnet
Nature Communications (2023)
-
Giant valley-Zeeman coupling in the surface layer of an intercalated transition metal dichalcogenide
Nature Materials (2023)
-
Fe Doping-Induced Magnetic Solitons in CrNb3S6
Journal of Electronic Materials (2023)
-
Cavity-enhanced linear dichroism in a van der Waals antiferromagnet
Nature Photonics (2022)
-
Melting of generalized Wigner crystals in transition metal dichalcogenide heterobilayer Moiré systems
Nature Communications (2022)