Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Evidence for a higher-order topological insulator in a three-dimensional material built from van der Waals stacking of bismuth-halide chains

Nature Materials volume 20, pages 473–479 (2021)Cite this article

Subjects

Abstract

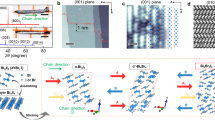
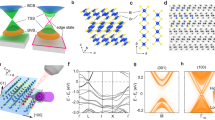
Low-dimensional van der Waals materials have been extensively studied as a platform with which to generate quantum effects. Advancing this research, topological quantum materials with van der Waals structures are currently receiving a great deal of attention. Here, we use the concept of designing topological materials by the van der Waals stacking of quantum spin Hall insulators. Most interestingly, we find that a slight shift of inversion centre in the unit cell caused by a modification of stacking induces a transition from a trivial insulator to a higher-order topological insulator. Based on this, we present angle-resolved photoemission spectroscopy results showing that the real three-dimensional material Bi4Br4 is a higher-order topological insulator. Our demonstration that various topological states can be selected by stacking chains differently, combined with the advantages of van der Waals materials, offers a playground for engineering topologically non-trivial edge states towards future spintronics applications.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Stacking-dependent topological properties in Bi4X4 (where X is Br or I).
Fig. 2: Hinges in the cleaved surface of semiconducting Bi4Br4.
Fig. 3: ARPES mapping for the bulk band structure of Bi4Br4.
Fig. 4: Experimental band structures of topological hinge states by laser ARPES.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding authors upon request.

References

  1. Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).

    Article  Google Scholar 

  2. Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  CAS  Google Scholar 

  3. Rasche, B. et al. Stacked topological insulator built from bismuth-based graphene sheet analogues. Nat. Mater. 12, 422–425 (2013).

    Article  CAS  Google Scholar 

  4. Liu, C.-C., Zhou, J.-J., Yao, Y. & Zhang, F. Weak topological insulators and composite Weyl semimetals: β-Bi4X4 (X = Br, I). Phys. Rev. Lett. 116, 066801 (2016).

    Article  Google Scholar 

  5. Noguchi, R. et al. A weak topological insulator state in quasi-one-dimensional bismuth iodide. Nature 566, 518–522 (2019).

    Article  CAS  Google Scholar 

  6. Zhang, F., Kane, C. L. & Mele, E. J. Surface state magnetization and chiral edge states on topological insulators. Phys. Rev. Lett. 110, 046404 (2013).

    Article  Google Scholar 

  7. Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).

    Article  Google Scholar 

  8. Matsugatani, A. & Watanabe, H. Connecting higher-order topological insulators to lower-dimensional topological insulators. Phys. Rev. B 98, 205129 (2018).

    Article  Google Scholar 

  9. Po, H. C., Vishwanath, A. & Watanabe, H. Symmetry-based indicators of band topology in the 230 space groups. Nat. Commun. 8, 50 (2017).

    Article  Google Scholar 

  10. Song, Z., Zhang, T., Fang, Z. & Fang, C. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 9, 3530 (2018).

    Article  Google Scholar 

  11. Zhang, T. et al. Catalogue of topological electronic materials. Nature 566, 475–479 (2019).

    Article  CAS  Google Scholar 

  12. Vergniory, M. G. et al. A complete catalogue of high-quality topological materials. Nature 566, 480–485 (2019).

    Article  CAS  Google Scholar 

  13. Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 566, 486–489 (2019).

    Article  CAS  Google Scholar 

  14. Khalaf, E., Po, H. C., Vishwanath, A. & Watanabe, H. Symmetry indicators and anomalous surface states of topological crystalline insulators. Phys. Rev. X 8, 031070 (2018).

    CAS  Google Scholar 

  15. Schindler, F. et al. Higher-order topology in bismuth. Nat. Phys. 14, 918–924 (2018).

    Article  CAS  Google Scholar 

  16. Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).

    Article  CAS  Google Scholar 

  17. Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925–929 (2018).

    Article  CAS  Google Scholar 

  18. Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).

    Article  CAS  Google Scholar 

  19. Xue, H., Yang, Y., Gao, F., Chong, Y. & Zhang, B. Acoustic higher-order topological insulator on a kagome lattice. Nat. Mater. 18, 108–112 (2019).

    Article  CAS  Google Scholar 

  20. Ni, X., Weiner, M., Alù, A. & Khanikaev, A. B. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nat. Mater. 18, 113–120 (2019).

    Article  CAS  Google Scholar 

  21. Kempkes, S. N. et al. Robust zero-energy modes in an electronic higher-order topological insulator. Nat. Mater. 18, 1292–1297 (2019).

    Article  CAS  Google Scholar 

  22. von Benda, H., Simon, A. & Bauhofer, W. Zur Kenntnis von BiBr und BiBr1,167. Z. Anorg. Allg. Chem. 438, 53–67 (1978).

    Article  Google Scholar 

  23. Filatova, T. et al. Electronic structure, galvanomagnetic and magnetic properties of the bismuth subhalides Bi4I4 and Bi4Br4. J. Solid State Chem. 180, 1103–1109 (2007).

    Article  CAS  Google Scholar 

  24. Zhou, J.-J., Feng, W., Liu, C.-C., Guan, S. & Yao, Y. Large-gap auantum spin Hall insulator in single layer bismuth monobromide Bi4Br4. Nano Lett. 14, 4767–4771 (2014).

    Article  CAS  Google Scholar 

  25. Zhou, J.-J., Feng, W., Liu, G.-B. & Yao, Y. Topological edge states in single- and multi-layer Bi4Br4. New J. Phys. 17, 015004 (2015).

    Article  CAS  Google Scholar 

  26. Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Efficient topological materials discovery using symmetry indicators. Nat. Phys. 15, 470–476 (2019).

    Article  CAS  Google Scholar 

  27. Hsu, C.-H. et al. Purely rotational symmetry-protected topological crystalline insulator α-Bi4Br4. 2D Mater. 6, 031004 (2019).

    Article  CAS  Google Scholar 

  28. Li, X. et al. Pressure-induced phase transitions and superconductivity in a quasi-one-dimensional topological crystalline insulator α-Bi4Br4. Proc. Natl Acad. Sci. USA 116, 17696–17700 (2019).

    Article  CAS  Google Scholar 

  29. Fang, C. & Fu, L. New classes of topological crystalline insulators having surface rotation anomaly. Sci. Adv. 5, eaat2374 (2019).

    Article  Google Scholar 

  30. Zhang, T. et al. Topological crystalline insulators with C2 rotation anomaly. Phys. Rev. Res. 1, 012001 (2019).

    Article  CAS  Google Scholar 

  31. Lai, K., Kundhikanjana, W., Kelly, M. & Shen, Z. X. Modeling and characterization of a cantilever-based near-field scanning microwave impedance microscope. Rev. Sci. Instrum. 79, 063703 (2008).

    Article  CAS  Google Scholar 

  32. Lv, B., Qian, T. & Ding, H. Angle-resolved photoemission spectroscopy and its application to topological materials. Nat. Rev. Phys. 1, 609–626 (2019).

    Article  Google Scholar 

  33. Shimojima, T., Okazaki, K. & Shin, S. Low-temperature and high-energy-resolution laser photoemission spectroscopy. J. Phys. Soc. Jpn 84, 72001 (2015).

    Article  Google Scholar 

  34. Zhang, P. et al. A precise method for visualizing dispersive features in image plots. Rev. Sci. Instrum. 82, 043712 (2011).

    Article  CAS  Google Scholar 

  35. Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).

    Article  CAS  Google Scholar 

  36. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    Article  CAS  Google Scholar 

  37. Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).

    Article  CAS  Google Scholar 

  38. Alexeev, E. M. et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 567, 81–86 (2019).

    Article  CAS  Google Scholar 

  39. Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).

    Article  CAS  Google Scholar 

  40. Jin, C. et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019).

    Article  CAS  Google Scholar 

  41. Hsu, C.-H., Stano, P., Klinovaja, J. & Loss, D. Majorana Kramers pairs in higher-order topological insulators. Phys. Rev. Lett. 121, 196801 (2018).

    Article  CAS  Google Scholar 

  42. Jäck, B. et al. Observation of a Majorana zero mode in a topologically protected edge channel. Science 364, 1255–1259 (2019).

    Article  Google Scholar 

  43. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    Article  CAS  Google Scholar 

  44. Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).

    Article  CAS  Google Scholar 

  45. Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).

    Article  CAS  Google Scholar 

  46. Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).

    Article  CAS  Google Scholar 

  47. Kresse, G. & Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).

    Article  CAS  Google Scholar 

  48. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).

    Article  CAS  Google Scholar 

  49. Becke, A. D. & Johnson, E. R. A simple effective potential for exchange. J. Chem. Phys. 124, 221101 (2006).

    Article  Google Scholar 

  50. Blaha, P. et al. WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties (Techn. Universitat, 2018).

  51. Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).

    Article  CAS  Google Scholar 

  52. Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).

    Article  Google Scholar 

  53. Kuneš, J. et al. Wien2wannier: from linearized augmented plane waves to maximally localized Wannier functions. Comput. Phys. Commun. 181, 1888–1895 (2010).

    Article  Google Scholar 

  54. Pizzi, G. et al. Wannier90 as a community code: new features and applications. J. Phys. Condens. Matter 32, 165902 (2020).

    Article  CAS  Google Scholar 

  55. Yaji, K. et al. High-resolution three-dimensional spin- and angle-resolved photoelectron spectrometer using vacuum ultraviolet laser light. Rev. Sci. Instrum. 87, 53111 (2016).

    Article  Google Scholar 

  56. Dudin, P. et al. Angle-resolved photoemission spectroscopy and imaging with a submicrometre probe at the SPECTROMICROSCOPY-3.2L beamline of Elettra. J. Synchrotron Radiat. 17, 445–450 (2010).

    Article  CAS  Google Scholar 

  57. Ishida, Y. & Shin, S. Functions to map photoelectron distributions in a variety of setups in angle-resolved photoemission spectroscopy. Rev. Sci. Instrum. 89, 043903 (2018).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

We thank D. Hamane for SEM characterization of the sample surface. We also thank X. Ma and D. Abeysinghe for their support in the exfoliation of Bi4Br4 samples. The work done at Tokyo Institute of Technology was supported by a CREST project [JPMJCR16F2] from Japan Science and Technology Agency (JST). The GISAXS experiments were performed under the approval of PF-PAC number 2018G661. We thank Diamond Light Source for access to beamline I05 under proposal SI20445, which contributed to the results presented here. Use of the Stanford Synchrotron Radiation Lightsource at the SLAC National Accelerator Laboratory is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. The MIM work was supported by the United States Army Research Office under grant number W911NF-17-1-0542. This work was supported by the JSPS KAKENHI (grant numbers JP18H01165, JP18K03484, JP19H02683, JP19F19030 and JP19H00651), and by MEXT Q-LEAP (grant number JPMXS0118068681). R.N. acknowledges support by JSPS under KAKENHI grant number JP18J21892 and support by JSPS through the Program for Leading Graduate Schools (ALPS). This work was also supported by MEXT under the “Program for Promoting Researches on the Supercomputer Fugaku” (Basic Science for Emergence and Functionality in Quantum Matter Innovative Strongly Correlated Electron Science by Integration of “Fugaku” and Frontier Experiments) (Project ID: hp200132).

Author information

Authors and Affiliations

  1. Institute for Solid State Physics, The University of Tokyo, Kashiwa, Japan

    Ryo Noguchi, Kenta Kuroda, Peng Zhang, Chun Lin, Cédric Bareille, Shunsuke Sakuragi, Hiroaki Tanaka, So Kunisada, Kifu Kurokawa, Koichiro Yaji, Ayumi Harasawa, Shik Shin & Takeshi Kondo

  2. Materials and Structures Laboratory, Tokyo Institute of Technology, Yokohama, Japan

    Masaru Kobayashi, Takanari Takahashi & Takao Sasagawa

  3. Department of Physics, University of Texas at Austin, Austin, TX, United States

    Zhanzhi Jiang, Zifan Xu, Daehun Lee & Keji Lai

  4. RIKEN Center for Emergent Matter Science (CEMS), Wako, Japan

    Motoaki Hirayama & Ryotaro Arita

  5. Department of Physics, Osaka University, Toyonaka, Japan

    Masayuki Ochi

  6. National Metrology Institute of Japan, National Institute of Advanced Industrial Science and Technology, Tsukuba, Japan

    Tetsuroh Shirasawa

  7. Elettra Synchrotron Trieste, Basovizza, Italy

    Viktor Kandyba, Alessio Giampietri & Alexei Barinov

  8. Diamond Light Source, Didcot, United Kingdom

    Timur K. Kim & Cephise Cacho

  9. Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Makoto Hashimoto & Donghui Lu

  10. Office of University Professor, The University of Tokyo, Kashiwa, Japan

    Shik Shin

  11. Department of Applied Physics, University of Tokyo, Tokyo, Japan

    Ryotaro Arita

  12. Trans-scale Quantum Science Institute, The University of Tokyo, Tokyo, Japan

    Takeshi Kondo

Authors
  1. Ryo Noguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Masaru Kobayashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhanzhi Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Kenta Kuroda
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Takanari Takahashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Zifan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Daehun Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Motoaki Hirayama
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Masayuki Ochi
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Tetsuroh Shirasawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Peng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Chun Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Cédric Bareille
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Shunsuke Sakuragi
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Hiroaki Tanaka
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. So Kunisada
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Kifu Kurokawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Koichiro Yaji
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. Ayumi Harasawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. Viktor Kandyba
    View author publications

    You can also search for this author in PubMed Google Scholar

  21. Alessio Giampietri
    View author publications

    You can also search for this author in PubMed Google Scholar

  22. Alexei Barinov
    View author publications

    You can also search for this author in PubMed Google Scholar

  23. Timur K. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  24. Cephise Cacho
    View author publications

    You can also search for this author in PubMed Google Scholar

  25. Makoto Hashimoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  26. Donghui Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  27. Shik Shin
    View author publications

    You can also search for this author in PubMed Google Scholar

  28. Ryotaro Arita
    View author publications

    You can also search for this author in PubMed Google Scholar

  29. Keji Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

  30. Takao Sasagawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  31. Takeshi Kondo
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

T.K. and T. Sasagawa planned the experimental project. R.N. conducted ARPES experiments and analysed the data. K. Kuroda, P.Z., C.L., C.B., S. Sakuragi, H.T., S.K., K. Kurokawa, K.Y., A.H., V.K., A.G., A.B., T.K.K., C.C., M. Hashimoto, D. Lu, S. Shin and T.K. supported the ARPES experiment. R.N., Z.J., Z.X., D. Lee and K.L. performed MIM experiments and analysed the data. M.K., T.T. and T. Sasagawa made and characterized Bi4Br4 single crystals and performed transport experiments. R.N. and M.K. collected laser microscope images. T. Shirasawa performed the GISAXS experiments. R.N. performed the SEM experiment. T. Sasagawa, M. Hirayama, M.O. and R.A. calculated the band structure and analysed the band topology. R.N., Z.J., K. Kuroda, M. Hirayama, M.O., T. Shirasawa, K.L., T. Sasagawa and T.K. wrote the paper. All authors discussed the results and commented on the manuscript.

Corresponding authors

Correspondence to Takao Sasagawa or Takeshi Kondo.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Materials thanks Xingjiang Zhou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Notes 1–14, Figs. 1–4 and references.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Noguchi, R., Kobayashi, M., Jiang, Z. et al. Evidence for a higher-order topological insulator in a three-dimensional material built from van der Waals stacking of bismuth-halide chains. Nat. Mater. 20, 473–479 (2021). https://doi.org/10.1038/s41563-020-00871-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41563-020-00871-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing