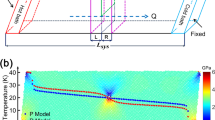
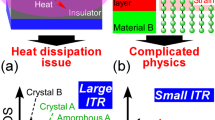
Abstract
Dislocations, one-dimensional lattice imperfections, are common to technologically important materials such as III–V semiconductors, and adversely affect heat dissipation in, for example, nitride-based high-power electronic devices. For decades, conventional nonlinear elasticity models have predicted that this thermal resistance is only appreciable when the heat flux is perpendicular to the dislocations. However, this dislocation-induced anisotropic thermal transport has yet to be seen experimentally. Using time-domain thermoreflectance, we measure strong thermal transport anisotropy governed by highly oriented threading dislocation arrays throughout micrometre-thick, single-crystal indium nitride films. We find that the cross-plane thermal conductivity is almost tenfold higher than the in-plane thermal conductivity at 80 K when the dislocation density is ~3 × 1010 cm−2. This large anisotropy is not predicted by conventional models. With enhanced understanding of dislocation–phonon interactions, our results may allow the tailoring of anisotropic thermal transport with line defects, and could facilitate methods for directed heat dissipation in the thermal management of diverse device applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data sets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Li, D. et al. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 83, 2934–2936 (2003).
Chen, S. et al. Thermal conductivity of isotopically modified graphene. Nat. Mater. 11, 203–207 (2012).
Broido, D. A., Malorny, M., Birner, G., Mingo, N. & Stewart, D. A. Intrinsic lattice thermal conductivity of semiconductors from first principles. Appl. Phys. Lett. 91, 231922 (2007).
Ma, J., Li, W. & Luo, X. Intrinsic thermal conductivity and its anisotropy of wurtzite InN. Appl. Phys. Lett. 105, 082103 (2014).
Wang, T., Carrete, J., van Roekeghem, A., Mingo, N. & Madsen, G. K. H. Ab initio phonon scattering by dislocations. Phys. Rev. B 95, 245304 (2017).
Katre, A., Carrete, J., Dongre, B., Madsen, G. K. H. & Mingo, N. Exceptionally strong phonon scattering by B substitution in cubic SiC. Phys. Rev. Lett. 119, 075902 (2017).
Polanco, C. A. & Lindsay, L. Ab initio phonon point defect scattering and thermal transport in graphene. Phys. Rev. B 97, 014303 (2018).
Yan, Z., Liu, G., Khan, J. M. & Balandin, A. A. Graphene quilts for thermal management of high-power GaN transistors. Nat. Commun. 3, 827 (2012).
Zhang, Q. et al. High thermoelectric performance by resonant dopant indium in nanostructured SnTe. Proc. Natl Acad. Sci. USA 110, 13261–13266 (2013).
Klemens, P. G. The scattering of low-frequency lattice waves by static imperfections. Proc. Phys. Soc. A 68, 1113–1128 (1955).
Carruthers, P. Scattering of phonons by elastic strain fields and the thermal resistance of dislocations. Phys. Rev. 114, 995–1001 (1959).
Kogure, Y. & Hiki, Y. Scattering of lattice waves by static strain fields in crystals. J. Phys. Soc. Jpn 36, 1597–1607 (1974).
Kneeze, G. A. & Granato, A. V. Effect of independent and coupled vibrations of dislocations on low-temperature thermal conductivity in alkali halides. Phys. Rev. B 25, 2851–2866 (1982).
Li, M. et al. Nonperturbative quantum nature of the dislocation–phonon interaction. Nano Lett. 17, 1587–1594 (2017).
O’Hara, S. G. & Anderson, A. C. Scattering of thermal phonons by dislocations in superconducting lead and tantalum. Phys. Rev. B 10, 574–579 (1974).
Nihira, T. & Iwata, T. Thermal resistivity changes in electron-irradiated pyrolytic-graphite. Jpn J. Appl. Phys. 14, 1099–1104 (1975).
Jo, I., Pettes, M. T., Ou, E., Wu, W. & Shi, L. Basal-plane thermal conductivity of few-layer molybdenum disulfide. Appl. Phys. Lett. 104, 201902 (2014).
Sun, B. et al. Temperature dependence of anisotropic thermal conductivity tensor of bulk black phosphorus. Adv. Mater. 29, 1603297 (2017).
Sproull, R. L., Moss, M. & Weinstock, H. Effect of dislocations on the thermal conductivity of lithium fluoride. J. Appl. Phys. 30, 334–337 (1959).
Su, Z. et al. Layer-by-layer thermal conductivities of the Group III nitride films in blue/green light emitting diodes. Appl. Phys. Lett. 100, 201106 (2012).
Mion, C., Muth, J. F., Preble, E. A. & Hanser, D. Accurate dependence of gallium nitride thermal conductivity on dislocation density. Appl. Phys. Lett. 89, 092123 (2006).
Loitsch, B., Schuster, F., Stutzmann, M. & Koblmüller, G. Reduced threading dislocation densities in high-T/N-rich grown InN films by plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 102, 051916 (2013).
Ju, J. et al. Trade-off between morphology, extended defects, and compositional fluctuation induced carrier localization in high In-content InGaN films. J. Appl. Phys. 116, 053501 (2014).
Gallinat, C. S., Koblmüller, G., Wu, F. & Speck, J. S. Evaluation of threading dislocation densities in In- and N-face InN. J. Appl. Phys. 107, 053517 (2010).
Cahill, D. G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 75, 5119–5122 (2004).
Sun, B. & Koh, Y. K. Understanding and eliminating artifact signals from diffusely scattered pump beam in measurements of rough samples by time-domain thermoreflectance (TDTR). Rev. Sci. Instrum. 87, 064901 (2016).
Feser, J. P., Liu, J. & Cahill, D. G. Pump–probe measurements of the thermal conductivity tensor for materials lacking in-plane symmetry. Rev. Sci. Instrum. 85, 104903 (2014).
Jiang, P., Huang, B. & Koh, Y. K. Accurate measurements of cross-plane thermal conductivity of thin films by dual-frequency time-domain thermoreflectance (TDTR). Rev. Sci. Instrum. 87, 075101 (2016).
Luckyanova, M. N. et al. Anisotropy of the thermal conductivity in GaAs/AlAs superlattices. Nano Lett. 13, 3973–3977 (2013).
Kwon, S., Zheng, J., Wingert, M. C., Cui, S. & Chen, R. Unusually high and anisotropic thermal conductivity in amorphous silicon nanostructures. ACS Nano 11, 2470–2476 (2017).
Jiang, P., Lindsay, L., Huang, X. & Koh, Y. K. Interfacial phonon scattering and transmission loss in >1 μm thick silicon-on-insulator thin films. Phys. Rev. B 97, 195308 (2018).
Jiang, P., Lindsay, L. & Koh, Y. K. Role of low-energy phonons with mean-free-paths >0.8 μm in heat conduction in silicon. J. Appl. Phys. 119, 245705 (2016).
Vermeersch, B., Carrete, J. & Mingo, N. Cross-plane heat conduction in thin films with ab-initio phonon dispersions and scattering rates. Appl. Phys. Lett. 108, 193104 (2016).
Dong, Z. S. & Zhao, C. W. Measurement of strain fields in an edge dislocation. Physica B Condens. Matter 405, 171–174 (2010).
Katcho, N. A., Carrete, J., Li, W. & Mingo, N. Effect of nitrogen and vacancy defects on the thermal conductivity of diamond: an ab initio Green’s function approach. Phys. Rev. B 90, 094117 (2014).
Masataka, H. & Toshiaki, M. High-quality InN film grown on a low-temperature-grown GaN intermediate layer by plasma-assisted molecular-beam epitaxy. Jpn J. Appl. Phys. 41, L540 (2002).
Yoshiki, S., Nobuaki, T., Akira, S., Tsutomu, A. & Yasushi, N. Growth of high-electron-mobility InN by RF molecular beam epitaxy. Jpn J. Appl. Phys. 40, L91 (2001).
Gallinat, C. S. et al. In-polar InN grown by plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 89, 032109 (2006).
Romanov, A. E. & Speck, J. S. Stress relaxation in mismatched layers due to threading dislocation inclination. Appl. Phys. Lett. 83, 2569–2571 (2003).
Huang, B. & Koh, Y. K. Improved topological conformity enhances heat conduction across metal contacts on transferred graphene. Carbon 105, 268–274 (2016).
Koh, Y. K. & Cahill, D. G. Frequency dependence of the thermal conductivity of semiconductor alloys. Phys. Rev. B 76, 075207 (2007).
Minnich, A. J. et al. Thermal conductivity spectroscopy technique to measure phonon mean free paths. Phys. Rev. Lett. 107, 095901 (2011).
Regner, K. T. et al. Broadband phonon mean free path contributions to thermal conductivity measured using frequency domain thermoreflectance. Nat. Commun. 4, 1640 (2013).
Wilson, R. B. & Cahill, D. G. Anisotropic failure of Fourier theory in time-domain thermoreflectance experiments. Nat. Commun. 5, 5075 (2014).
Mohammed, A. M. S. et al. Fractal Lévy heat transport in nanoparticle embedded semiconductor alloys. Nano Lett. 15, 4269–4273 (2015).
Peierls, R. E. Quantum Theory of Solids (Clarendon Press, 1955).
Ziman, J. M. Electrons and Phonons. The Theory of Transport Phenomena in Solids (Oxford Univ. Press, Oxford, 1960).
Srivastava, G. P. The Physics of Phonons (Taylor & Francis, Abingdon, 1990).
Omini, M. & Sparavigna, A. Beyond the isotropic-model approximation in the theory of thermal conductivity. Phys. Rev. B 53, 9064–9073 (1996).
Lindsay, L., Broido, D. A. & Reinecke, T. L. Thermal conductivity and large isotope effect in GaN from first principles. Phys. Rev. Lett. 109, 095901 (2012).
Lindsay, L., Broido, D. A. & Reinecke, T. L. Ab initio thermal transport in compound semiconductors. Phys. Rev. B 87, 165201 (2013).
Mingo, N., Stewart, D. A., Broido, D. A., Lindsay, L. & Li, W. in Length-Scale Dependent Phonon Interactions (eds Shindé, S. L. & Srivastava, G. P.) 137–173 (Springer, New York, 2014).
Lindsay, L. First principles Peierls–Boltzmann phonon thermal transport: a topical review. Nanosc. Microsc. Therm. 20, 67–84 (2016).
Acknowledgements
The authors thank R. Wang and B. Huang at NUS for help with the thermal evaporation of Al films. The authors thank M. Li at MIT for explanation of his papers. This work was supported by an NUS Start-up Grant, the Singapore Ministry of Education Academic Research Fund Tier 2 under award no. MOE2013-T2–2–147 and Singapore Ministry of Education Academic Research Fund Tier 1 FRC project FY2016. C.P. and L.L. acknowledge support from the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division and computational resources from the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under contract no. DE-AC02-05CH11231. G.K. acknowledges support from the excellence program Nanosystems Initiative Munich (NIM) funded by the German Research Foundation (DFG).
Author information
Authors and Affiliations
Contributions
G.K. and Y.K.K. initialized the idea. B.S. and Y.K.K. designed the experiments. B.S. performed the TDTR measurements and analysed the data. G.H., J.Z.J. and G.K. prepared and characterized the InN samples. C.P. and L.L. performed the first-principles and phonon-defect scattering calculations. All authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary information
Supplementary Notes 1–5, Supplementary Figures 1–16, Supplementary Tables 1–4, Supplementary References 1–30
Rights and permissions
About this article
Cite this article
Sun, B., Haunschild, G., Polanco, C. et al. Dislocation-induced thermal transport anisotropy in single-crystal group-III nitride films. Nature Mater 18, 136–140 (2019). https://doi.org/10.1038/s41563-018-0250-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-018-0250-y
This article is cited by
-
Low thermal contact resistance boron nitride nanosheets composites enabled by interfacial arc-like phonon bridge
Nature Communications (2024)
-
Strain evolution and confinement effect in InAs/AlAs short-period superlattices studied by Raman spectroscopy
Scientific Reports (2023)
-
Diffusion metamaterials
Nature Reviews Physics (2023)
-
Dislocation-based high-temperature plasticity of polycrystalline perovskite SrTiO3
Journal of Materials Science (2023)
-
Inelastic phonon transport across atomically sharp metal/semiconductor interfaces
Nature Communications (2022)