Abstract
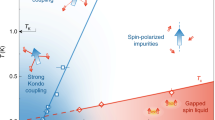
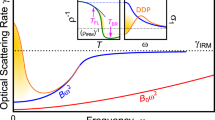
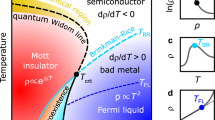
The localization of charge carriers by electronic repulsion was suggested by Mott in the 1930s to explain the insulating state observed in supposedly metallic NiO. The Mott metal–insulator transition has been subject of intense investigations ever since1,2,3—not least for its relation to high-temperature superconductivity4. A detailed comparison to real materials, however, is lacking because the pristine Mott state is commonly obscured by antiferromagnetism and a complicated band structure. Here we study organic quantum spin liquids, prototype realizations of the single-band Hubbard model in the absence of magnetic order. Mapping the Hubbard bands by optical spectroscopy provides an absolute measure of the interaction strength and bandwidth—the crucial parameters that enter calculations. In this way, we advance beyond conventional temperature–pressure plots and quantitatively compose a generic phase diagram for all genuine Mott insulators based on the absolute strength of the electronic correlations. We also identify metallic quantum fluctuations as a precursor of the Mott insulator–metal transition, previously predicted but never observed. Our results suggest that all relevant phenomena in the phase diagram scale with the Coulomb repulsion U, which provides a direct link to unconventional superconductivity in cuprates and other strongly correlated materials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Gebhard, F. The Mott Metal–Insulator Transition (Springer, Berlin, 1997).
Imada, M., Fujimori, A. & Tokura, Y. Metal–insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Vollhardt, D. Dynamical mean-field theory for correlated electrons. Ann. Phys. 524, 1–19 (2012).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Vučičević, J., Terletska, H., Tanasković, D. & Dobrosavljević, V. Finite-temperature crossover and the quantum Widom line near the Mott transition. Phys. Rev. B 88, 075143 (2013).
Xu, L. et al. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl Acad. Sci. USA 102, 16558 (2005).
Simeoni., G. G. et al. The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 6, 503–507 (2010).
Richardson, R. C. The Pomeranchuk effect. Rev. Mod. Phys. 69, 683–690 (1997).
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Itou, T., Oyamada, A., Maegawa, S., Tamura, M. & Kato, R. Quantum spin liquid in the spin-1∕2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 77, 104413 (2008).
Shimizu, Y. et al. Pressure-Tuned Exchange Coupling of a Quantum Spin Liquid in the Molecular Triangular Lattice κ−(ET)2Ag2(CN)3. Phys. Rev. Lett. 117, 107203 (2016).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Powell, B. J. & McKenzie, R. H. Quantum frustration in organic Mott insulators: from spin liquids to unconventional superconductors. Rep. Prog. Phys. 74, 056501 (2011).
Hotta, C. Theories on frustrated electrons in two-dimensional organic solids. Crystals 2, 1155–1200 (2012).
Faltermeier, D. et al. Bandwidth-controlled Mott transition in κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1–x: optical studies of localized charge excitations. Phys. Rev. B 76, 165113 (2007).
Dressel, M. et al. Lattice vibrations of the charge-transfer salt κ-(BEDT-TTF)2Cu2(CN)3: comprehensive explanation of the electrodynamic response in a spin-liquid compound. Phys. Rev. B 93, 081201 (2016).
Kandpal, H. C., Opahle, I., Zhang, Y.-Z., Jeschke, H. O. & Valentí, R. Revision of model parameters for κ-type charge transfer salts: an ab initio Study. Phys. Rev. Lett. 103, 067004 (2009).
Kato, R. & Hengbo, C. Cation dependence of crystal structure and band parameters in a series of molecular conductors, β′-(Cation)[Pd(dmit)2]2 (dmit: 1,3-dithiole-2-thione-4,5-dithiolate). Crystals 2, 861–874 (2012).
Furukawa, T., Miyagawa, K., Taniguchi, H., Kato, R. & Kanoda, K. Quantum criticality of Mott transition in organic materials. Nat. Phys. 11, 221–224 (2015).
Nakamura, Y., Hiramatsu, T., Yoshida, Y., Saito, G. & Kishida, H. Optical properties of a quantum spin liquid candidate material, κ-(BEDT-TTF)2Ag2(CN)3. J. Phys. Soc. Jpn 86, 014710 (2017).
Kezsmarki, I. et al. Depressed charge gap in the triangular-lattice Mott insulator κ−(ET)2Cu2(CN)3. Phys. Rev. B 74, 201101 (2006).
Terletska, H., Vučičević, J., Tanasković, D. & Dobrosavljević, V. Quantum critical transport near the Mott transition. Phys. Rev. Lett. 107, 026401 (2011).
Pinterić, M. et al. Anisotropic charge dynamics in the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 90, 195139 (2014).
Pinteric, M. et al. Anions effects on the electronic structure and electrodynamic properties of the Mott insulator κ-(BEDT-TTF)2Ag2(CN)3. Phys. Rev. B 94, 161105 (2016).
Lazić, P. et al. Importance of van der Waals interactions and cation–anion coupling in an organic quantum spin liquid. Phys. Rev. B 97, 245134 (2018).
Limelette, P. et al. Universality and critical behavior at the Mott transition. Science 302, 89–92 (2003).
Kagawa, F., Miyagawa, K. & Kanoda, K. Unconventional critical behaviour in a quasi-two-dimensional organic conductor. Nature 436, 534–537 (2005).
Gati, E. et al. Breakdown of Hooke’s law of elasticity at the Mott critical endpoint in an organic conductor. Sci. Adv. 2, e1601646 (2016).
Pustogow, A. et al. Nature of optical excitations in the frustrated kagome compound herbertsmithite. Phys. Rev. B 96, 241114(R) (2017).
Hansmann, P. et al. Mott–Hubbard transition in V2O3 revisited. Phys. Stat. Sol. B 250, 1251–1264 (2013).
Qazilbash, M. M. et al. Electrodynamics of the vanadium oxides VO2 and V2O3. Phys. Rev. B 77, 115121 (2008).
Sordi, G., Sémon, P., Haule, K. & Tremblay, A.-M. S. Pseudogap temperature as a Widom line in doped Mott insulators. Sci. Rep. 2, 547 (2012).
Pustogow, A. Unveiling Electronic Correlations in Layered Molecular Conductors by Optical Spectroscopy. PhD Thesis, University of Stuttgart (2017).
Kato, R., Fukunaga, T., Yamamoto, H. M., Ueda, K. & Hengbo, C. Crystal structure and band parameters of mixed crystals derived from quantum spin liquid β′-EtMe3Sb[Pd(dmit)2]2 (dmit: 1,3-dithiole-2-thione-4,5-dithiolate). Phys. Stat. Solidi B 249, 999–1003 (2012).
Kato, R. Development of pi-Electron Systems Based on [M(dmit)2] (M = Ni and Pd; dmit: 1,3-dithiole-2-thione-4,5-dithiolate) Anion Radicals. Bull. Chem. Soc. Jpn 87, 355–374 (2014).
Geiser, U. et al. Superconductivity at 2.8 K and 1.5 kbar in κ-(BEDT-TTF)2Cu2(CN)3: the first organic superconductor containing a polymeric copper cyanide anion. Inorg. Chem. 30, 2586 (1991).
Hiramatsu, T. et al. Design and preparation of a quantum spin liquid candidate κ-(ET)2Ag2(CN)3 having a nearby superconductivity. Bull. Chem. Soc. Jpn 90, 1073–1082 (2017).
Dressel, M. & Grüner, G. Electrodynamics of Solids (Cambridge Univ. Press, Cambridge, 2002).
Gorshunov, B. P. et al. Terahertz BWO-spectroscopy. Int. J. Infrared Millim. Waves 26, 1217–1240 (2005).
Yasin, S. et al. Transport studies at the Mott transition of the two-dimensional organic metal κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1–x. Eur. Phys. J. B 79, 383–390 (2011).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Jarrell, M. & Gubernatis, J. E. Bayesian inference and the analytic continuation of imaginary-time quantum Monte Carlo data. Phys. Rep. 269, 133–195 (1996).
Acknowledgements
We thank K. Kanoda and R. Valentí for fruitful discussions. Part of the work is supported by the Deutsche Forschungsgemeinschaft via DR228/41-1 and DR228/48-1. We also thank the Deutscher Akademischer Austauschdienst for support. This work was partially supported by JSPS KAKENHI grant no. JP16H06346. We acknowledge the Russian Ministry of Education and Science (Program ‘5 top 100’). We also acknowledge support from the Croatian Science Foundation project IP-2013-11-1011. J.A.S. acknowledges support from the Independent Research and Development program from the NSF while working at the Foundation and from the National High Magnetic Field Laboratory User Collaboration Grants Program. Work in Florida was supported by the NSF grant no. DMR-1410132, and the National High Magnetic Field Laboratory through the NSF cooperative agreement no. DMR-1157490 and the State of Florida. Parts of the text and results reported in this work are reproduced from the thesis of A.P.33 at the University of Stuttgart, and accessible at https://doi.org/10.18419/opus-9487.
Author information
Authors and Affiliations
Contributions
Most of the optical experiments and their analysis were conducted by A.P. with the help of M.B. The terahertz measurements were performed by E.Z. and B.G. Crystal growth and d.c. transport measurements on EtMe crystals were performed by R.K., and d.c. transport on AgCN and CuCN was measured by R.R. and A.L., respectively. The AgCN salts were grown by A.L., R.H., T.H., Y.Y. and G.S., and the CuCN crystals by A.L., R.H. and J.S. Theoretical calculations were carried out by T.-H.L. and V.D. in communication with S.F. The interpretation and draft of the manuscript were made by A.P. and M.D. who also conceived the project. All the authors contributed to the discussion and the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–8, Supplementary Table 1, Supplementary Figures 1–16, Supplementary References 1–31
Rights and permissions
About this article
Cite this article
Pustogow, A., Bories, M., Löhle, A. et al. Quantum spin liquids unveil the genuine Mott state. Nature Mater 17, 773–777 (2018). https://doi.org/10.1038/s41563-018-0140-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-018-0140-3
This article is cited by
-
Band transport evidence in PEDOT:PSS films using broadband optical spectroscopy from terahertz to ultraviolet region
Communications Materials (2024)
-
Chasing the spin gap through the phase diagram of a frustrated Mott insulator
Nature Communications (2023)
-
Thermodynamic determination of the equilibrium first-order phase-transition line hidden by hysteresis in a phase diagram
Scientific Reports (2023)
-
Disorder-dominated quantum criticality in moiré bilayers
Nature Communications (2022)
-
Entropic evidence for a Pomeranchuk effect in magic-angle graphene
Nature (2021)