Abstract
Countries have sought to stop the spread of coronavirus disease 2019 (COVID-19) by severely restricting travel and in-person commercial activities. Here, we analyse the supply-chain effects of a set of idealized lockdown scenarios, using the latest global trade modelling framework. We find that supply-chain losses that are related to initial COVID-19 lockdowns are largely dependent on the number of countries imposing restrictions and that losses are more sensitive to the duration of a lockdown than its strictness. However, a longer containment that can eradicate the disease imposes a smaller loss than shorter ones. Earlier, stricter and shorter lockdowns can minimize overall losses. A ‘go-slow’ approach to lifting restrictions may reduce overall damages if it avoids the need for further lockdowns. Regardless of the strategy, the complexity of global supply chains will magnify losses beyond the direct effects of COVID-19. Thus, pandemic control is a public good that requires collective efforts and support to lower-capacity countries.
Similar content being viewed by others
Main
COVID-19, which is caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), emerged in late December 2019, but quickly spread to other countries1 in Asia, Europe and North America and was declared a pandemic by the World Health Organization (WHO) on 11 March 2020 (ref. 2). There are now confirmed individuals with COVID-19 in nearly every country of the world, and the WHO has urged affected countries to slow the spread of the virus by imposing containment and suppression measures3,4 ranging from strict controls on travel, social gatherings and commercial activities aimed at ‘flattening the curve’ (that is, decreasing the rate of new infections to avoid overwhelming healthcare systems) to less strict measures designed to shield immunologically compromised individuals, treat victims and achieve ‘herd immunity’ (that is, a sufficiently large number of recovered and, therefore, immune individuals to prevent the effective spread of the virus)5. Differences in the strictness of such policies and the rapidity with which jurisdictions have imposed and relaxed the policies reflect divergent (and perhaps hasty) assessments of both the public health risk of COVID-19 and the social and economic impacts of the different policies6,7. Using a newly developed economic disaster model8,9,10, we quantitatively assess the short-run supply-chain effects of different containment strategies across countries and industry sectors to inform ongoing efforts to contain COVID-19 and to reveal more generally how pandemic-related economic losses will be distributed along global supply chains.
Details of our analytical approach are provided in the Methods. In summary, we modelled the short-term economic shocks of different COVID-19 response scenarios as sector-specific transportation and labour supply constraints. The model operates in weekly time steps using the latest available global input–output data11 and taking into account interactions throughout complex global supply chains and the contexts of scarcity and imbalance that prevail in most markets9. Our enhanced adaptive regional input–output (ARIO) model incorporates substitutability of inputs and dynamic choices of supply-chain linkages (Supplementary Fig. 1), which contribute to a more realistic representation of bottlenecks along global supply chains. By applying our model to the simulation of control policies during a pandemic, we can assess the potential impact of different policies on the supply chains and examine the externalities of control measures. Note that our model is distinct from computable general equilibrium (CGE) models in that it is specifically designed to assess economic impacts in response to disasters that unfold over weeks or months, before production structures and trade networks have time to adjust to new production patterns. Moreover, the goal of this study is not to predict the true cost of the COVID-19 pandemic, but to identify the most important aspects of disease control (such as strictness, duration and recurrence of lockdowns) and test the sensitivity of these factors as their impacts ripple through global supply chains, supported by several sets of scenarios for containment measures. Thus, in addition to showing how overall damages might change under different policy scenarios, the incidence of damages across sectors and countries may inform the allocation of international aid and economic stimulus.
We modelled four different sets of pandemic scenarios, three of which (36 scenarios in total) represent different spread extents and containment responses to the COVID-19 pandemic (Fig. 1, Table 1 and Supplementary Fig. 2), and the last of which (3 scenarios in total) assesses both the damages of sustaining some restrictions over a longer period as well as the losses if lockdowns are imposed again next autumn or winter. Spatial spread refers to the global extent of the pandemic—the number of countries affected. Duration refers to the number of months that lockdown measures are in place. Strictness is measured by the percentage by which labour availability and transportation capacity12 are reduced relative to pre-pandemic levels. Given that the impacts of lockdown measures on labour availability depend on the characteristics of production, we developed specific impact-to-labour ‘multipliers’ for each sector on the basis of three factors: the level of exposure to the virus (that is, the degree and proximity of in-person interactions), essential or lifeline sectors (such as electricity), and the option of performing work from home (for example, education). Sector-specific constraints on labour availability are therefore determined by both the strictness of lockdown measures represented in the scenario (for example, 80% strictness will reduce overall transportation capacity by 80%) and the sector-specific multipliers (for example, 0.5 for wheat production as the level of exposure is low and 0.1 for electricity and gas supply as essential activities; see Methods). Each of the 39 scenarios is based on a different combination of spatial spread, duration and strictness; the results are presented in terms of economic supply-chain effects, measured in absolute terms of loss in value added (for example, billions of US dollars) or relative terms (as a percentage of pre-pandemic value added).
a–i, Maps of the results from 9 scenarios out of the first three sets of 36 modelled scenarios, with different combinations of spatial spread (China only (a,d,g), Europe and the United States (b,e,h), and global (c,f,i)), lockdown duration and strictness (80%–2 month (a–c), 60%–4 month (d–f) and 60%–6 month (g–i); see Methods; Table 1). Strictness represents the level of reductions in transportation capacity and labour availability relative to pre-pandemic levels. The percentages at the bottom left of each map indicate the global value-added losses for each scenario; shading denotes the regional distributions of these losses. j–l, A summary of all 36 scenarios, showing the sensitivity of global value-added losses to duration (different stacks) and strictness (shading of stacked bars) for the China only (j), Europe and the United States (k), and the global scenarios (l).
Results
Figure 1 summarizes the results of several representative pandemic scenarios. The panels in the left column (Fig. 1a,d,g,j) show the supply-chain effects if COVID-19 had been successfully contained to only China; the panels in the middle column (Fig. 1b,e,h,k) show the impact if COVID-19 had spread from China to Europe and the United States, which had implemented lockdowns, but no further; and the panels in the right column (Fig. 1c,f,i,l) show the impact when the virus spreads globally and all of the remaining countries implemented containment measures. Although some of these results are outdated given the reality of the global spread of the disease, it may nonetheless be useful to examine the differences in impacts as a function of spatial spread (Supplementary Information). For each of the different spatial spreads (Fig. 1, columns), Fig. 1 also shows the results of 3 different lockdown strictness–duration combinations: from 80% restriction for 2 months (Fig. 1a–c) to 60% restriction for 6 months (Fig. 1g–i). Note that China’s lockdown is consistently modelled as an 80% restriction for the 2 months of January and February13 in the scenarios of greater spatial spread, with restrictions in Europe and the United States beginning in March, and restrictions in the remaining countries (in the global scenario) beginning in April (see Methods; Supplementary Fig. 2).
The first insight from the model is that the global cost of the pandemic depends foremost on the number of affected countries, and then on the required duration of lockdown policies; by contrast, the strictness of these policies is comparatively less important. The spatial extent of the pandemic is the most important driver of the global cost. If only China had been affected, our results suggest that the global supply-chain effects (measured by value added) would have been 3.5% of global gross domestic product (GDP; Fig. 1a). With the spread to highly developed western countries and the containment measures placed in Europe and the United States, we found that the global supply-chain effects increase almost fourfold to 12.6% (Fig. 1b). Finally, the modelled impacts of global lockdowns in response to COVID-19 are greater still—26.8% of global GDP (Fig. 1c). The magnitude of lockdown duration is shown in Fig. 1f,i, which shows the effects of global spread and relatively strict (60%) lockdowns for 4 and 6 months. In this case, global value-added losses increase slightly more than 4% (from 26.3% to 30.8%; Fig. 1f,i).
Figure 1j–l further emphasizes the rapid increase in global losses with the duration of lockdowns. For example, in the strictest lockdown scenarios (that is, 80%) with global spread, the global supply-chain effects rise from US$20.0 trillion under a 2-month duration (Fig. 1l, blue bars) to US$22.7 trillion under a 4-month duration (Fig. 1l, green bars) and US$30.1 trillion (equivalent to 40.3% of global value added) under a 6-month duration (Fig. 1l, red bars). However, the same bar charts show that global losses are relatively less sensitive to the strictness of lockdown measures compared with the extent of pandemic or duration of the lockdown. For example, if only China had been affected (China only scenario; Supplementary Fig. 3), doubling the strictness would lead to an almost linear impact under a 2-month duration. As the duration increases, the economic damage is less sensitive to changes in strictness. In the global scenario, the global impacts of 2 months of lockdown are only 7.2% greater under a strictness of 80% compared with a strictness of 20% (Fig. 1l, dark and light blue bars). Although both duration and strictness determine the domestic production (through labour supply) and transportation capacity—which links upstream suppliers to downstream consumers—the economic damages through supply-chain linkages are much more sensitive to the duration of the measures.
The second insight from the model is the importance of propagation through global supply chains—even countries that are not directly affected by the virus experience large losses, and low- and middle-income countries are more vulnerable to indirect effects. Figure 2 shows direct effects (that is, due to domestic containment measures, such as lockdown or suppression; Fig. 2, hashed areas of the bars) and propagation effects through international supply chains across the three scenarios sets (Fig. 2, solid areas of the bars). In the scenarios in which an outbreak is contained in China, direct losses, by definition, occur only in China, but are nonetheless substantial—16.7% of China’s annual GDP (Fig. 2a). However, even if the virus had been confined to China, its economic disruption would not have been. Forward and backward propagations along supply chains within China and with other countries add another 4.8% to China’s losses to cause overall impacts of 21.5% of annual value added. For example, although the United States and New Zealand are not directly affected by COVID-19 in this scenario, they would still suffer 0.6% and 2.2% value-added losses, respectively, during a lockdown with 80% strictness for 2 months in China due to the decline in China’s output (that is, negative forward effects) as well as a decrease in China’s final demand for their products (negative backward effect). Under the same scenario, countries such as Vietnam, Malaysia and Nigeria, which are closely linked to China’s supply chains, would experience decreases of 5.2%, 3.6% and 3.1% in their GDP, respectively. Interestingly, specialized economies such as Kazakhstan (energy), Mongolia (livestock) and Jamaica (tourism) experience even larger losses, with 6.1%, 4.2% and 11.4% decreases in their annual GDP, respectively (Fig. 2d–i). Similarly, countries where the virus has been controlled can be continuously affected by imported losses. Assuming the virus is controlled in China over two months but spreads globally, China nonetheless suffers ongoing economic disruption due to propagations—US$5.77 trillion in the global scenario in which lockdowns are 40% strict for 6 months (Supplementary Fig. 2).
a–i, Economic loss (measured by the percentage of value-added losses) in the following nine selected countries: China (a), New Zealand (b), United States (c), Vietnam (d), Nigeria (e), Malaysia (f), Kazakhstan (g), Jamaica (h) and Mongolia (i). The top row country includes China (affected in the China only scenario), developed countries such as the United States (affected in the Europe and US scenario) and New Zealand (only affected in the global scenario). The middle row includes countries (affected in the global scenario) that have close supply-chain relationships with China to assess propagation effects. The bottom row includes countries with a dominant economic sector. Each plot contains three selected scenarios from the three scenario sets (12 per figure as indicated). The shades of blue, green and red indicate a duration of 2, 4 and 6 months, respectively. The hashed area in the bars represents direct losses due to containments and the solid area represents the propagation. The results of other selected countries are provided in Supplementary Figs. 4–11.
Lockdown losses are propagated through supply-chain networks14. In particular, unaffected countries benefit enormously from effective containment measures in affected countries. For example, if only China had been affected, most of the supply-chain effects in other countries would have been delayed by weeks or months (depending on which country; Supplementary Fig. 2), as firms used their inventories to smoothen the shock. Specifically, with 2 months of the strictest lockdown measures in China but with no spread of the virus beyond China (that is, China only, 80%–2-month scenario; Fig. 2, top blue bars), our results indicate that 21.6% of China’s value added is lost, while the impacts in other countries are much smaller compared with scenarios in which those countries are also directly affected (that is, the global scenario; Fig. 2).
Similarly, if the virus had been contained in those highly developed western countries by a strict 2-month containment (that is, the Europe and the United States 80%–2-month scenario; Fig. 2, centre blue bars), Europe and the United States would suffer much larger direct losses of 15–20% of their GDP. The economic damage in countries that are not directly affected increases with the duration of lockdowns in affected countries. For example, the loss in Ethiopia will increase from 2.5% under the Europe and the US 80%–2-month lockdown scenario to 9.8% under a 6-month lockdown (Supplementary Fig. 2). But this is still much less than the 27.9% losses in Ethiopia under the scenario of global spread and 6 months of 40% strict lockdowns. Although these findings are too late to affect public health policies for the first round of the COVID-19 pandemic, they demonstrate that containment has both substantial positive externalities, in that all countries benefited considerably when China placed the strictest measures, and negative externalities, in that all countries suffer from containment in other countries due to reduced demand in global markets. However, our estimates show that the positive externality of containments dominates.
The third insight is that specific country sectors are quite vulnerable to impacts that are propagated through global supply chains, even in scenarios in which COVID-19 does not spread globally. Figures 3 and 4 show the upstream and downstream impacts related to the Chinese electronics and German automotive sectors, respectively. Each of these sectors are important to the respective economies of China and Germany and each are also dependent on extensive international supply chains.
a–f, The supply-chain impacts to China’s electronic-manufacturing industries under three scenario sets (China only, 80%–2 month (a,b); Europe and the United States, 60%–4 month (c,d); and global, 40%–6 month (e,f)). The economic impacts to China’s electronics industry’s upstream supply chain (a,c,e) and the economic impacts from the perspective of downstream supply chains (b,d,f) are shown. The different colours of each bar represent the strength of linkage between industries and China’s electronics industry (blue to red). In the upstream supply chains, bars coloured towards the red end of the colour scale indicate that the suppliers are more important for China’s electronics industry; downstream, the bars coloured towards the red end of the colour scale indicate that these sectors are the main clients of China’s electronics industry. The length of the bars in a–f shows the industries’ relative production losses compared with the original capacity under different scenario sets. The colours of the bars represent the cohesion level of the particular sector to the Chinese electronics sector from blue (weak) to red (strong), which is measured by the trade volume between the particular sector and the Chinese electronics sector. The results of some other industries in different countries are provided in Supplementary Figs. 12–14.
a–f, The economic impacts to supply chain upstream of German automobile industries (a,c,e) and the economic impacts from the perspective of downstream supply chain (b,d,f) under three scenario sets (China only, 80%–2 month (a,b); Europe and the United States, 60%–4 month (c,d); and global, 40%–6 month (e,f)). The colour and bar area are as described in Fig. 3. The length of bars in a–f show the industries’ relative production losses compared with the original capacity under different scenario sets. The colours of the bars represent the cohesion level of the particular sector to the German automotive sector from blue (weak) to red (strong), which is measured by the trade volume between the particular sector and the German automotive sector.
China’s electronics supply chain is labour intensive and has a ‘scale-free’ property7, that is, there is a clustered hub in China with connections to a large number of firms in electronics, chemical and metal production in countries throughout Asia15. In scenarios in which COVID-19 is confined to China by a strict 2-month lockdown (that is, the China only, 80%–2-month scenario), the global value added related to China’s electronics sector would have been reduced by 27.3% (including 20.8% in direct losses; Supplementary Fig. 15). However, the impacts to China’s electronics sector trigger substantial upstream decreases in production in the South Korean electronics, Japanese electronics and Australian metals sectors (in each case by roughly 21%; Fig. 3a). Although electronic products are largely substitutable, major production lines are centralized in China15, such that there are also large downstream impacts as reduced output limits final consumption, particularly in the United States, Japan, Mexico and France (where reductions are >28%; Fig. 3b). In the scenario of global spread and 6 months of lockdowns (that is, the global 40%–6-month scenario), the recovery of China’s labour supply and transportation capacity to pre-disaster levels does not prevent ongoing impacts to its electronics sector through global supply chains (largely forward effects from upstream Asian countries), which further increases the reduction in the sector’s output from 29.9% to 32.8% (Fig. 3e, Supplementary Fig. 15). In this global scenario, downstream consumption in countries such as the United States, Japan, Mexico and France is reduced by a total of 40% (Fig. 3f).
Automotive sectors are similarly international16, with highly specialized suppliers that make short-term substitution difficult17. In the scenario in which only China imposes lockdown measures (that is, the China only 80%–2-month scenario), supply-chain effects to the German automobile are modest—losses of 1.8% of value added as China’s demand for German motor parts and vehicles fall by around 20% (Fig. 4b, Supplementary Fig. 16) and reductions in the output of various Chinese sectors (such as electronics, metals, and rubber and plastics) constrain upstream production of motor parts in the United States and the United Kingdom and electronics in Germany. However, with the spread of COVID-19 to highly developed western countries (that is, the Europe and the United States 60%–4-month scenario), labour and transportation constraints in Germany and many of the countries that supply auto parts and raw materials (Supplementary Fig. 16) cause a decrease in production by the German automotive sector of 28.8% (24.8% directly due to local containment and 4.0% due to effects upstream; Fig. 4c). Such decreases in German production ripple upstream to suppliers in Hungary, Spain, Italy and the United States, and downstream demand for German cars decreases in the United States, China and Austria by 29.1%, 37.6% and 22.3%, respectively (Fig. 4d). In the case of global spread and more widespread and longer-term lockdowns (that is, the global 40%–6-month scenario; Fig. 4e), the output of the German automobile industries decreases by a further 0.9%. A decrease in supplies from low- and middle-income countries to Germany (Supplementary Fig. 16) leads German producers to look for new suppliers (substitution effect). By contrast, the production of motor parts in the United States rebounds slightly in this scenario, but the overall impacts of such global spread remain strongly negative everywhere. Consumption of German cars in the United States and Austria falls by 29.5% and—although Chinese demand for German cars in this scenario returns to pre-pandemic levels in April—supply-chain and transportation constraints nonetheless reduce Chinese consumption of German cars by 37.5%.
Our results also highlight the vulnerability of sectors such as catering and tourism to pandemic lockdowns18, which are exposed to both very large decreases in demand and the propagation of losses from upstream suppliers such as food and business sectors19. For example, in scenarios of a global pandemic (for example, the global 40%–6-month scenario), very large reductions in domestic and international travel and tourism (Supplementary Fig. 17) cause tourism in Jamaica to decrease by 56.3%, in turn reducing imports of beverages and tobacco products from the United States, which fall to 46.7% of pre-pandemic levels (Supplementary Fig. 17).
As a final analysis, we modelled three different scenarios of recovery from the global spread of the COVID-19 pandemic: (1) a ‘new normal’ scenario in which each country’s lockdown (China, 80%–2-month scenario; Europe and the United States, 60%–4-month scenario; all other countries, 40%–6-month scenario) was first relaxed to 20% strictness and then back to 0% over a period of 12 months. (2) A ‘recurrent with global cooperation’ scenario, in which (round 1) each country’s lockdown (that is, China, 80%–2 month; Europe and the United States, 60%–4 month; all other countries 40%–6 month) was first relaxed to 0% strictness over a period of 2 months, followed by a 3-month period of no restrictions, and then (round 2) all countries acted together by placing the strictest (80%), 2-month global lockdown to minimize virus spreading. (3) A ‘recurrent without global cooperation’ scenario, in which (round 1) each country’s lockdown (that is, China, 80%–2 month; Europe and the United States, 60%–4 month; all other countries, 40%–6 month) was first relaxed to 0% strictness over a period of 2 months, followed by a 3 month period of no restrictions, and then (round 2) all countries placed the same less strict but longer lockdowns as the first round.
These recovery scenarios led to a fourth and final insight—relaxing lockdown restrictions gradually over a long period of time (in our ‘new normal’ scenario, 12 months) results in substantially lower supply-chain effects than lifting restrictions quickly if it means avoiding another round of strict lockdowns in the coming year. Globally, we estimate that the overall value-added losses in the new normal scenario are 39.5%, compared with 49.5% and 61.5% in the recurrent with global cooperation and recurrent without global cooperation scenarios, respectively (Fig. 5a–c). The differences are particularly striking in the United States, where losses related to recurrent lockdowns are 24.6–54.8% greater compared with the losses in the scenario in which restrictions are slowly relaxed (Fig. 2d–f, light-blue shading). As shown in our scenarios of initial lockdowns, if the pandemic does recur, stricter and shorter lockdowns (which may depend on global coordination) also greatly reduce losses (11% globally) in our estimates (Fig. 5b,c). The implications of these different recovery trajectories for selected sectors are shown in Fig. 5g–i; similar to the losses globally or in specific countries, recurrent lockdowns are considerably worse for the selected sectors (for example, 33.1–90.8% worse in the sectors depicted).
a–c, The results from three post-pandemic recovery scenarios (new normal (a,d,g); recurrent with cooperation (b,e,h); recurrent without cooperation (c,f,i)), with different potential recovery strategies. The percentages in the bottom of each map indicate the global value-added losses. The colour shades represent the severity of economic impact by countries. d–f, The stacked area plots show the dynamics of value-added loss in different countries or regions. ROW, rest of the world. g–i, The value-added loss in ten selected sectors under different recovery trajectories.
Discussion
Our modelling of COVID-19 lockdowns demonstrates the potential for enormous economic losses in affected countries, using idealized scenarios in which the number of countries, the duration and the strictness of lockdowns, as well as the manner in which restrictions are relaxed as the pandemic abates, were varied. In each scenario, we used factors that are influenced or determined by public health policy choices across the globe20,21. Our model was designed to identify the most important containment factors and measure the magnitude of propagation effects through global supply chains. The analytical framework settings are fundamentally different from those used in other macroeconomic analyses22,23,24 that aim to estimate the costs of COVID-19. Our model is limited by taking no consideration of technological changes and assuming that production and consumption patterns are kept the same as before the crisis. Our model focuses on the short-term scenarios and situations after a shock and, therefore, those changes are rather unlikely. Our model is further constrained by the trade relationship at the sectoral level among countries, and has no ability to capture the complexity of supply-chain networks at the firm level and may therefore underestimate the total effects. Finally, it is not our purpose, nor our approach, to model the dynamic general equilibrium effects, or health-related implications, such as mortality, quality-adjusted life year and disability-adjusted life year. This paper therefore cannot compare the costs and benefits of various strategies, but focuses only on their economic implications.
We have enumerated several insights on the basis of our results, which together suggest that economic losses will be minimized by stricter initial lockdowns, provided that such strictness reduces the duration of the measures. Indeed, emerging results of related research seems to support exactly this relationship13. However, our modelling of recovery scenarios suggests that an extended period of some restrictions (for example, 20% reductions in labour and transportation capacity in our new normal scenario) is nonetheless economically preferable to a more rapid return to pre-pandemic activities followed by another round of global lockdowns. This is a critical, albeit perhaps inconvenient, finding for policymakers who are eager to lift restrictions and stimulate economic recovery.
Our results also illustrate the substantial and heterogenous impacts propagated through global supply chains, which affect the level of economic loss to a country or sector in ways that are not always intuitive. Moreover, just as individuals who stay at home protect others as well as themselves, countries that impose strict lockdowns also provide a public good to other countries25,26. For example, we estimate that a strict lockdown that contained the COVID-19 outbreak to China would have reduced global GDP by 3.5% while costing China 21% of its GDP. In theory, disease control measures should be increased up to the point at which the marginal social costs of control are just offset by the marginal social benefits. Our results imply that a large part of the problem that we currently face is that individual countries are making disease control choices without sufficient consideration of the effect of their actions on global supply chains. The positive externalities of public health measures to prevent a pandemic may lead to market failures, leading to underinvestment and delayed action from the perspective of global optimization. In preparing for the next emerging disease, a global cost-sharing instrument could ensure that the costs of monitoring, containing and suppressing are fairly distributed, removing some of the disincentives for early action and providing global health and economic benefits over the long term.
Methods
Disaster impact model to measure supply-chain effects
Our impact model is an extension of the ARIO model25,26, which is widely used in the literature to simulate the propagation of negative shocks throughout the economy27,28,29. Our model improves the ARIO model in two ways. The first improvement is related to the substitutability of products from the same sector sourced from different regions. Second, in our model, clients will choose their suppliers across regions on the basis of their capacity. These two improvements contribute to a more realistic representation of bottlenecks along global supply chains. Note that CGE models, which are often used for economic assessment, can also handle the above two points well, and there are some pioneering studies on improving the CGE model to make it better suited for short-run simulations by adjusting behavioural parameters within the model. For example, Rose and Guha30 proposed a CGE model for assessing electric utility lifeline losses from earthquakes. Some recent research also suggested that, if we have enough parameters, the CGE model can perform well in short-run simulations31. Considering that the globally validated parameter set—as well as the simulation of short-run consequences after COVID-19, in which adjustment through prices appears to be unlikely due to socioeconomic inertia, transaction costs and antigouging legislation—has not yet been estimated, here we adopted the improved ARIO model.
Our disaster impact model includes four main modules, that is, a production module, an allocation module, a demand module and a simulation module. The production module is designed for characterizing the firm’s production activities. The allocation module is used to describe how firms allocate output to their clients, including downstream firms (intermediate demand) and households (final demand); the demand module is used to describe how clients place orders to their suppliers; and the simulation module is designed for executing the whole simulation procedure.
Production module
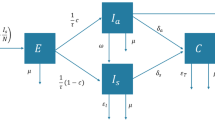
The production module is used to characterize production processes. Firms rent capital and employ labour to process natural resources and intermediate inputs produced by other firms into a specific product (Supplementary Fig. 1). The production process for firm i can be expressed as follows:
where xi denotes the output of the firm in monetary values; p denotes the type of intermediate products; \(z_i^p\) denotes intermediate products used in production processes; vai denotes the primary inputs to production, such as labour (L), capital (K) and natural resources (NR). f(∙) is the production function for firms. There are a wide range of functional forms, such as Leontief32, Cobb–Douglas and constant elasticity of substitution production function33. Different functional forms reflect the possibility for firms to substitute an input for another. Considering that epidemics often cause large-scale economic fluctuations in the short term, during which economic agents do not have enough time to adjust other inputs to substitute temporary shortages, we used the Leontief production function, which does not allow substitution between inputs.
where \(a_i^p\) and bi are the input coefficients calculated as
and
where the overbar indicates the value of that variable in the equilibrium state. In an equilibrium state, producers use intermediate products and primary inputs to produce goods and services to satisfy demand from their clients. After a disaster, output will decrease. From a production perspective, there are mainly the constraints described below.
Labour supply constraints
Labour constraints after a disaster may impose severe knock-on effects on the rest of the economy34,35,36. This makes labour constraints a key factor to consider in disaster impact analysis. For example, in the case of a pandemic, these constraints can arise from the inability of employees to work as a result of illness or death, or from the inability to go to work and the requirement to work at home (if possible). In this model, the proportion of surviving productive capacity from the constrained labour productive capacity (\(x_i^L\)) after a shock is defined as37,38,39:
Where \(\gamma _i^L(t)\) is the proportion of labour that is unavailable at each time step t during containment. \((1 - \gamma _i^L(t))\) contains the available proportion of employment at time t.
The proportion of the available productive capacity of labour is therefore a function of the losses from the sectoral labour forces and its pre-disaster employment level. Following the assumption of fixed input–output relationships, the productive capacity of labour in each region after a disaster (\(x_i^L\)) will represent a linear proportion of the available labour capacity at each time step40,41. Take COVID-19 as an example, during an outbreak of an infectious disease, authorities often adopt social distancing and other measures to reduce the risk of infection. This imposes an exogenous negative shock on the economic network.
Supply constraints
Firms will purchase intermediate products from their supplier in each period. Insufficient inventory of a firm’s intermediate products will create a bottleneck for production activities. The potential production level that the inventory of the pth intermediate product can support is
where \(S_i^p(t - 1)\) refers to the amount of pth intermediate products held by firm i at the end of time step t − 1.
Considering all of the limitations mentioned above, the maximum supply capacity of firm i can be expressed as
The actual production of firm i, \(x_i^a(t)\), depends on both its maximum supply capacity and the total orders the firm received from its clients, TDi(t − 1), (see the ‘Demand module’ section),
The inventory held by firm i will be consumed during the production process,
Allocation module
The allocation module mainly describes how suppliers allocate products to their clients. When some firms in the economic system suffer a negative shock, their production will be constrained by a shortage to primary inputs, such as a shortage of labour supply in the outbreak of COVID-19. In this case, the output of a firm will not be able to fulfil all of the orders of its clients. A rationing scheme that reflects a mechanism on the basis of which a firm allocates an insufficient amount of products to its clients is needed25,42. For this case study, we applied a proportional rationing scheme according to which a firm allocates its output in proportion to its orders. Under the proportional rationing scheme, the amount of products of firm i allocated to firm j, \({\mathrm{FRC}}_j^i\left( t \right)\) and household h, \({\mathrm{HRC}}_h^i\left( t \right)\), is as follows,
where \({\mathrm{FOD}}_i^j(t - 1)\) refers to the order issued by firm j to its supplier i in time step t − 1, and \({\mathrm{HOD}}_i^h(t - 1)\) refers to the order issued by household h to its supplier j. Firm j received intermediates to restore its inventories,
Therefore, the amount of intermediate p held by firm i at the end of period t is
Demand module
The demand module represents a characterization of how firms and households issue orders to their suppliers at the end of each period. A firm orders from its supplier owing to the need to restore its intermediate product inventory. We assume that each firm has a specific target inventory level, equal to a given number of days, \(n_i^p\), of intermidiate consumption9, on the basis of its maximum supply capacity in each time step,
Then, the order issued by firm i to its supplier j is
Households issue orders to their suppliers on the basis of their demand and the supply capacity of their suppliers. In this study, the demand of household h to final products q, \(HD_h^q\left( t \right)\), is given exogenously at each time step. Then, the order issued by household h to its supplier j is
The total order received by firm j is
Simulation module
At each time step, the actions of firms and households are as follows:
-
1.
Firms plan and execute their production based on three factors: (1) inventories of intermediate products they have, (2) supply of primary inputs and (3) orders from their clients. Firms will maximize their output under these constraints.
-
2.
Product allocation: firms allocate outputs to clients based on their orders. In equilibrium, the output of firms just meets all orders. When production is constrained by exogenous negative shocks, outputs may not cover all orders. In this case, we use a proportional rationing scheme that was proposed previously25,42 (see the ‘Allocation module’ section) to allocate products of firms.
-
3.
Firms and households issue orders to their suppliers for the next time step. Firms place orders with their suppliers based on the gaps in their inventories (target inventory level minus existing inventory level). Households place orders with their suppliers based on their demand. When a product comes from multiple suppliers, the allocation of orders is adjusted according to the production capacity of each supplier.
This discrete-time dynamic procedure can reproduce the equilibrium of the economic system, and can simulate the propagation of exogenous shocks, both from the firm and household side or transportation disruptions, in the economic network. From the firm side, if the supply of a firm’s primary inputs is constrained, it will have two effects. On the one hand, the decrease in output at this firm means that the orders of its clients cannot be fulfilled. This will result in a decrease in inventory of these clients, which will constrain their production. This is the so-called forward or downstream effect. By contrast, less output in this firm also means less use of intermediate products from its suppliers. This will reduce the number of orders it places with its suppliers, which will further reduce the production level of its suppliers. This is the so-called backward or upstream effect. Similarly, these two effects can also occur if the transport of a firm to its clients or suppliers is restricted. For example, during the outbreak of COVID-19 in China, the authorities adopted strict isolation measures. These measures have placed constraints on the supply of labour and the transportation of products. This resulted in a decrease in China’s output and also triggered the forward and backward effect, leading to the propagation of the shock through the global economic production web. From the household side, the fluctuation of household demand caused by exogenous shocks will also trigger the aforementioned backward effect. For example, in the case of tourism, during the outbreak of COVID-19 in China, the demand for visiting China from tourists all over the world will decrease substantially. This influence will further propagate to the accommodation and catering industry as well as their suppliers through supplier–client links.
Supply-chain effects and economic losses
We define the value-added decrease of all firms in a network caused by an exogenous negative shock as the disaster impacts of the shock. Note that, in our estimates, whereas we considered economic impacts of the lockdowns, we were not looking at dynamic general equilibrium effects, mortality, quality-adjusted life year and disability-adjusted life year. For the firm directly affected by exogenous negative shocks, its loss includes two parts: (1) the value-added decrease caused by exogenous constraints and (2) the value-added decrease caused by propagation. The former is the direct loss, while the latter is the indirect loss. A negative shock’s total economic impacts (TEIi,r), direct impacts (DEIi,r) and propagated impacts (PEIi,r) on a supply chain for firm i in region r are
Global supply-chain network
We built a global supply-chain network on the basis of the Global Trade Analysis Project (GTAP) database11 version 10. GTAP 10 provides a multiregional input–output (MRIO) table for the year 2014. This MRIO table divides the world into 141 economies, each of which contains 65 production sectors. If we treat each sector as a firm (producer) and assume that each region has a representative household, we can obtain the following information from the MRIO table: (1) suppliers and clients of each firm; (2) suppliers for each household and (3) the flow of each supplier–client connection under the equilibrium state. This provides a benchmark for our model. It should be noted that the MRIO table provided by GTAP is only a sectoral level network, it cannot capture the complexity of supply-chain networks at the firm level. Thus, this study only serves as approximation of the actual effect. However, detailed data are rarely available, particularly those for supply chains in developing countries and for global supply chains across countries.
When applying such an aggregated network in the disaster impact model, we need to consider the substitutability of intermediate products supplied by suppliers from the same sector in different regions. The substitution between some intermediate products is fairly straightforward. For example, for a firm that extracts spices from bananas, it does not make much of a difference whether the bananas are sourced from the Philippines or Thailand. However, for a car manufacturing firm in Japan that uses screws from Chinese auto parts suppliers and engines from German auto parts suppliers to assemble cars, the products of the suppliers in these two regions cannot be substituted. If we assume that all goods cannot be substituted as in the traditional IO model, then we will overestimate the loss of producers, such as the fragrance extraction firm. If we assume that products from suppliers in the same sector can be completely substitutable, then we will substantially underestimate the losses of producers such as Japanese car manufacturing firm. To alleviate the shortcomings of the evaluation deviation under the two assumptions, we set the possibility of substitution for each firm on the basis of the region and sector of supplier supply (see the ‘Allocation module’ section).
Spread and containment scenarios
The number of affected countries, the duration of the containment and the strictness of the containment are the three important factors that influence the loss caused by the epidemic. Using these three indicators as dimensions and then referring to the actual epidemic situation, we designed three sets of scenarios, that is, China only, Europe and the United States, and global. Different sets of scenarios represent different areas of influence of COVID-19, while scenarios in the same scenario set have different assumptions about the duration and strictness of the containment.
Our first scenario set, China only, assumes that the outbreak of COVID-2019 is only in mainland China. In this scenario set, labour supply and transportation in mainland China was restricted owing to the need for epidemic control from the fourth week of 2020 (that is, 22 January 2020). To examine the impact of policy strictness and duration of the outbreak on the world economic system, we set four levels of strictness (that is, 20%, 40%, 60% and 80%) and three durations (that is, 2, 4 and 6 months) (Table 1). For example, the scenario ‘China only 20%–2 month’ means that the epidemic lasts for two months with labour supply and transportation restrictions of 20%.
Isolation measures have different effects on labour supply in different sectors. We set a specific multiplier for each sector on the basis of three factors, that is, the exposure level of the sector’s work, whether it is the lifeline and whether it is possible to work at home. If a sector’s work exposure level is low, it is the lifeline sector or it is easy to work at home, the sector’s multiplier will be small, and vice versa.
Then, the constraints on labour supply in each sector are determined by two parts, that is, the benchmark constraint in the scenario and multipliers for the sector. For example, we assume that the multiplier for the wheat production sector is 0.5 because the level of exposure to its production activities is relatively low. Then, in the China only 20%–2-month scenario, the labour supply in the wheat production sector will fall by 10%, that is, 20% multiplied by 0.5. At the same time, in the scenario set, transportation between mainland China and other regions will also fall by 50% throughout the duration of the epidemic.
The epidemic not only affects the global economic system from the supply side, but also affects economic output through its impact on consumer demand. Tourism demand for the region with COVID-2019 outbreaks will drop considerably. Owing to a lack of data, we assumed that the final demand for the two sectors—recreation and other services, and accommodation, food and service activities—in the outbreaking area fell by 99% during the duration of the outbreak.
In the second set of scenarios (Europe and the United States), we assumed that regions with the current severe epidemic situation have taken measures from the eleventh week (11 March 2020) to control their epidemic. These countries include the United States, France, Germany, Italy, the Netherlands, the United Kingdom, Switzerland, Spain and Iran. The labour and transportation restrictions are consistent with the settings of the scenario set China only, and take the China only 80%–2-month scenario as the default in mainland China, which matches with the reality shown in the Baidu big data.
In the final set of scenarios (global), we assumed that, in addition to mainland China and the economies in the scenario set Europe and the United States, other economies in the world also began to take measures to control the epidemic in the fifteenth week (8 April 2020). The labour and transportation restrictions are consistent with the settings of the scenario sets China only and Europe and the United States, and take the China only 80%–2-month scenario as default for mainland China and the Europe and the United States 60%–4-month scenario as default in economies in the scenario set Europe and the United States.
Finally, we designed and modelled three post-pandemic scenarios of recovery as follows:
-
Pandemic as a new normal scenario: starting in January 2020, China only placed 80% strictness for 2 months, which was then reduced to 20% for 12 months. EU and the United States placed 60% strictness for 4 months, which was then reduced to 20% strictness for 12 months. Global placed 40% strictness for 6 months, which was then reduced to 20% and gradually relaxed to 0% over a period of 12 months.
-
Recurrent pandemic scenario with global cooperation: starting in January 2020, each country’s lockdown (that is, China, 80%–2 month; Europe and the United States, 60%–4 month; all other countries, 40%–6 month) was first relaxed to 0% strictness over a period of 2 months, followed by a 3-month period of no restrictions and then another round of strict (80%), 2-month global lockdown starting in January 2021.
-
Recurrent pandemic scenario without global cooperation: starting in January 2020, each country’s lockdown (that is, China, 80%–2 month; Europe and the United States, 60%–4 month; all other countries, 40%–6 month) was first relaxed to 0% strictness over a period of 2 months, followed by a 3-month period of no restrictions, and then another round of the same less strict, longer lockdowns starting in January 2021, as the first round.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The global trade dataset used to stimulate the presented results are licensed by from the Global Trade Analysis Project at the Center for Global Trade Analysis in Purdue University’s Department of Agricultural Economics. The GTAP version 10 can be obtained for a fee from its official website: https://www.gtap.agecon.purdue.edu/databases/v10/index.aspx. Owing to the restriction in the licensing agreement with GTAP, the authors have no right to disclose the original dataset publicly.
Code availability
The simulation code can be accessed at https://github.com/DaopingW/economic-impact-model. The minimal input for the code is multiregional input–output table. The sample code and test data for the minimal inputs are also provided.
References
Li, Q. et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 382, 1199–1207 (2020).
Remuzzi, A. & Remuzzi, G. COVID-19 and Italy: what next? Lancet 395, 1225–1228 (2020).
Anderson, R. M., Heesterbeek, H., Klinkenberg, D. & Hollingsworth, T. D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 395, 931–934 (2020).
Hellewell, J. et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 8, E488–E496 (2020).
Shim, E., Tariq, A., Choi, W., Lee, Y. & Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 93, 339–344 (2020).
Wells, C. R. et al. Impact of international travel and border control measures on the global spread of the novel 2019 coronavirus outbreak. Proc. Natl Acad. Sci. USA 117, 7504–7509 (2020).
Inoue, H. & Todo, Y. Firm-level propagation of shocks through supply-chain networks. Nat. Sustain. 2, 841–847 (2019).
Zeng, Z., Guan, D., Steenge, A. E., Xia, Y. & Mendoza-Tinoco, D. Flood footprint assessment: a new approach for flood-induced indirect economic impact measurement and post-flood recovery. J. Hydrol. 579, 124204 (2019).
Hallegatte, S. Modeling the role of inventories and heterogeneity in the assessment of the economic costs of natural disasters. Risk Anal. 34, 152–167 (2014).
Hallegatte, S. An adaptive regional input-output model and its application to the assessment of the economic cost of Katrina. Risk Anal. 28, 779–799 (2008).
Aguiar, A., Chepeliev, M., Corong, E., McDougall, R. & Dominique, V. D. M. The GTAP Data Base: version 10. J. Glob. Econ. Anal. 4, 1–27 (2019).
Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: a simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transportation Res. E 136, 101922 (2020).
Qiu, Y., Chen, X. & Shi, W. Impacts of social and economic factors on the transmission of coronavirus disease (COVID-19) in China. J. Popul. Econ. https://doi.org/10.1007/s00148-020-00778-2 (2020).
Otto, C., Willner, S. N., Wenz, L., Frieler, K. & Levermann, A. Modeling loss-propagation in the global supply network: the dynamic agent-based model acclimate. J. Econ. Dyn. Control 83, 232–269 (2017).
Lukas, B. A., Tan, J. J. & Hult, G. T. M. Strategic fit in transitional economies: the case of China’s electronics industry. J. Manag. 27, 409–429 (2001).
Mazur, C., Contestabile, M., Offer, G. J. & Brandon, N. P. Understanding the drivers of fleet emission reduction activities of the German car manufacturers. Environ. Innov. Soc. Transit. 16, 3–21 (2015).
Ceryno, P. S., Scavarda, L. F. & Klingebiel, K. Supply chain risk: empirical research in the automotive industry. J. Risk Res. 18, 1145–1164 (2015).
Kuo, H.-I., Chen, C.-C., Tseng, W.-C., Ju, L.-F. & Huang, B.-W. Assessing impacts of SARS and avian flu on international tourism demand to Asia. Tour. Manag. 29, 917–928 (2008).
Wamboye, E. F., Nyaronga, P. J. & Sergi, B. S. What are the determinant of international tourism in Tanzania? World Dev. Perspect. 17, 100175 (2020).
Smith, R. D., Keogh-Brown, M. R. & Barnett, T. Estimating the economic impact of pandemic influenza: an application of the computable general equilibrium model to the UK. Soc. Sci. Med. 73, 235–244 (2011).
Luo, S. Propagation of financial shocks in an input-output economy with trade and financial linkages of firms. Rev. Econ. Dyn. 36, 246–269 (2020).
Ludvigson, S. C., Ma, S. & Ng, S. Covid19 and the Macroeconomic Effects of Costly Disasters Working Paper Series No. 26987 (National Bureau of Economic Research, 2020).
Barro, R. J., Ursúa, J. F. & Weng, J. The Coronavirus and the Great Influenza Pandemic: Lessons from the ‘Spanish Flu’ for the Coronavirus’s Potential Effects on Mortality and Economic Activity Working Paper Series No. 26866 https://doi.org/10.3386/w26866 (National Bureau of Economic Research, 2020).
Maliszewska, M. Aaditya, M. & van der Mensbrugghe, D. The Potential Impact of COVID-19 on GDP and Trade: A Preliminary Assessment Policy Research Working Paper No. 9211 (World Bank, 2020).
Wenz, L. & Levermann, A. Enhanced economic connectivity to foster heat stress-related losses. Sci. Adv. 2, e1501026 (2016).
Rowan, N. J. & Laffey, J. G. Challenges and solutions for addressing critical shortage of supply chain for personal and protective equipment (PPE) arising from Coronavirus disease (COVID19) pandemic—case study from the Republic of Ireland. Sci. Total Environ. 725, 138532 (2020).
Koks, E. E. & Thissen, M. A multiregional impact assessment model for disaster analysis. Econ. Syst. Res. 28, 429–449 (2016).
Okuyama, Y. & Santos, J. R. Disaster impact and input-output analysis. Econ. Syst. Res. 26, 1–12 (2014).
Li, J., Crawford-Brown, D., Syddall, M. & Guan, D. Modeling imbalanced economic recovery following a natural disaster using input-output analysis. Risk Anal. 33, 1908–1923 (2013).
Rose, A. & Guha, G.-S. in Modeling Spatial and Economic Impacts of Disasters (eds Okuyama, Y. & Chang, S. E.) 119–141 (Springer, 2004).
Yamazaki, M., Koike, A. & Sone, Y. A heuristic approach to the estimation of key parameters for a monthly, recursive, dynamic CGE model. Econ. Disaster. Clim. Change 2, 283–301 (2018).
Miller, R. E. & Blair, P. D. Input-Output Analysis: Foundations and Extensions 2nd edn (Cambridge Univ. Press, 2009).
Inoue, H. & Todo, Y. Propagation of negative shocks across nationwide firm networks. PLoS ONE 14, e0213648 (2019).
Zhang, Z., Li, N., Xu, H. & Chen, X. Analysis of the economic ripple effect of the United States on the world due to future climate change. Earths Future 6, 828–840 (2018).
Corong, E. The standard GTAP model: version 7. J. Glob. Econ. Anal. 2, 1–119 (2017).
Xia, Y. et al. Assessment of the economic impacts of heat waves: a case study of Nanjing, China. J. Clean. Prod. 171, 811–819 (2018).
Koks, E. E. et al. Regional disaster impact analysis: comparing input-output and computable general equilibrium models. Nat. Hazards Earth Syst. Sci. 16, 1911–1924 (2016).
Zeng, Z. & Guan, D. Methodology and application of flood footprint accounting in a hypothetical multiple two-flood event. Philos. Trans. R. Soc. A 378, 20190209 (2020).
Xia, Y. et al. Assessing the economic impacts of IT service shutdown during the York flood of 2015 in the UK. Proc. R. Soc. A 475, 20180871 (2019).
Matsuo, H. Implications of the Tohoku earthquake for Toyota's coordination mechanism: supply chain disruption of automotive semiconductors. Int. J. Prod. Econ. 161, 217–227 (2015).
Steenge, A. E. & Bockarjova, M. Thinking about imbalances in post-catastrophe economies: an input–output based proposition. Econ. Syst. Res. 19, 205–223 (2007).
Bénassy, J.-P. Nonclearing markets: microeconomic concepts and macroeconomic applications. J. Econ. Lit. 31, 732–761 (1993).
Acknowledgements
This study was supported by the National Natural Science Foundation of China (grant nos. 71988101, 91846301, 41629501 and 41921005), National Key R&D Program of China (grant no. 2016YFA0600104), the Czech Science Foundation under the project VEENEX (GA ČR no. 16-17978S). We acknowledge supports from the World Bank Group and Tsinghua University Initiative Scientific Research Program and donations from Delos Living LLC and the Cyrus Tang Foundation to Tsinghua University. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
D.G. and S.H. designed the study. D.W. and D.G. performed the analysis. D.G., D.W., S.H., S.J.D., J.H. and K.H. prepared the manuscript. D.W., S.H., S.J.D. X. Liang and S.W. interpreted supply-chain data and results. X.Lu compiled the international transportation data. Q.X., D.Cheng. and P.C. prepared the Supplementary Information. S.L, Y.B. and T.L. prepared the figures. D.G. coordinated and S.H. supervised the project. D.Coffman, B.X. and P.G. participated in the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Peer review reports are available. Primary Handling Editors: Aisha Bradshaw and Stavroula Kousta.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–17, Supplementary Table 1, Supplementary References and Supplementary Methods.
Rights and permissions
About this article
Cite this article
Guan, D., Wang, D., Hallegatte, S. et al. Global supply-chain effects of COVID-19 control measures. Nat Hum Behav 4, 577–587 (2020). https://doi.org/10.1038/s41562-020-0896-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41562-020-0896-8
This article is cited by
-
The Impact of Crises on Maritime Traffic: A Case Study of the COVID-19 Pandemic and the War in Ukraine
Networks and Spatial Economics (2024)
-
BO–SHAP–BLS: a novel machine learning framework for accurate forecasting of COVID-19 testing capabilities
Neural Computing and Applications (2024)
-
Influence of dynamic capabilities and supply chain finance on supply chain effectiveness in environmental dynamism: a conditional process analysis
Operations Management Research (2024)
-
Machine learning-based mathematical model for drugs and equipment resilient supply chain using blockchain
Annals of Operations Research (2024)
-
Robust optimization model of anti-epidemic supply chain under technological innovation: learning from COVID-19
Annals of Operations Research (2024)