Abstract
Progressive crystallization of Earth’s inner core drives convection in the outer core and magnetic field generation. Determining the rate and pattern of inner-core growth is thus crucial to understanding the evolution of the geodynamo. The growth history of the inner core is probably recorded in the distribution and strength of its seismic anisotropy, which arises from deformation texturing constrained by conditions at the inner-core solid–fluid boundary. Here we show from analysis of seismic body wave travel times that the strength of seismic anisotropy increases with depth within the inner core, and the strongest anisotropy is offset from Earth’s rotation axis. Then, using geodynamic growth models and mineral physics calculations, we simulate the development of inner-core anisotropy in a self-consistent manner. From this we find that an inner core composed of hexagonally close-packed iron–nickel alloy, deformed by a combination of preferential equatorial growth and slow translation, can match the seismic observations without requiring hemispheres with sharp boundaries. Our model of inner-core growth history is compatible with external constraints from outer-core dynamics, and supports arguments for a relatively young inner core (~0.5–1.5 Ga) and a viscosity >1018 Pa s.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The seismic travel-time measurements that support the findings of this study (Figs. 1, 2 and 4 and Extended Data Figs. 3, 5, 7 and 9) are available in Supplementary Data 1 and at https://doi.org/10.5281/zenodo.4721364. Raw seismic waveform data and metadata are accessible through the facilities of IRIS Data Services, and specifically the IRIS Data Management Center. The EHB Online Bulletins are available from the ISC; for access to the EHB see https://doi.org/10.31905/PY08W6S3.
Code availability
VPSC7 code is available on request from R. A. Lebensohn and information about accessing the code can be found at https://public.lanl.gov/lebenso/. GrowYourIC code is available at https://github.com/MarineLasbleis/GrowYourIC and this work uses version 0.6 (ref. 76). Plots were produced using Generic Mapping Tools77.
References
Poupinet, G., Pillet, R. & Souriau, A. Possible heterogeneity of the Earth’s core deduced from PKIKP travel times. Nature 305, 294–206 (1983).
Morelli, A., Dziewonski, A. M. & Woodhouse, J. H. Anisotropy of the inner core inferred from PKIKP travel times. Geophys. Res. Lett. 13, 1545–1548 (1986).
Woodhouse, J. H., Giardini, D. & Li, X. ‐D. Evidence for inner core anisotropy from free oscillations. Geophys. Res. Lett. 13, 1549–1552 (1986).
Lasbleis, M. & Deguen, R. Building a regime diagram for the Earth’s inner core. Phys. Earth Planet. Inter. 247, 80–93 (2015).
Lincot, A., Cardin, P., Deguen, R. & Merkel, S. Multiscale model of global inner-core anisotropy induced by hcp alloy plasticity. Geophys. Res. Lett. 43, 1084–1091 (2016).
Tanaka, S. & Hamaguchi, H. Degree one heterogeneity and hemispherical variation of anisotropy in the inner core from PKP(BC)–PKP(DF) times. J. Geophys. Res. Solid Earth 102, 2925–2938 (1997).
Creager, K. C. Large-scale variations in inner core anisotropy. J. Geophys. Res. Solid Earth 104, 23127–23139 (1999).
Irving, J. C. E. & Deuss, A. Hemispherical structure in inner core velocity anisotropy. J. Geophys. Res. Solid Earth 116, B04307 (2011).
Lythgoe, K. H., Deuss, A., Rudge, J. F. & Neufeld, J. A. Earth’s inner core: innermost inner core or hemispherical variations? Earth Planet. Sci. Lett. 385, 181–189 (2014).
Yoshida, S., Sumita, I. & Kumazawa, M. Growth model of the inner core coupled with the outer core dynamics and the resulting elastic anisotropy. J. Geophys. Res. Solid Earth 101, 28085–28103 (1996).
Aubert, J., Amit, H., Hulot, G. & Olson, P. Thermochemical flows couple the Earth’s inner core growth to mantle heterogeneity. Nature 454, 758–761 (2008).
Deguen, R., Cardin, P., Merkel, S. & Lebensohn, R. A. Texturing in Earth’s inner core due to preferential growth in its equatorial belt. Phys. Earth Planet. Inter. 188, 173–184 (2011).
Deguen, R., Alboussière, T. & Labrosse, S. Double-diffusive translation of Earth’s inner core. Geophys. J. Int. 214, 88–107 (2018).
Alboussière, T., Deguen, R. & Melzani, M. Melting-induced stratification above the Earth’s inner core due to convective translation. Nature 466, 744–747 (2010).
Monnereau, M., Calvet, M., Margerin, L. & Souriau, A. Lopsided growth of Earth’s inner core. Science 328, 1014–1017 (2010).
Lebensohn, R. A. & Tomé, C. N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys. Acta Metall. Mater. 41, 2611–2624 (1993).
Belonoshko, A. B. et al. Origin of the low rigidity of the Earth’s inner core. Science 316, 1603–1605 (2007).
Lincot, A., Merkel, S. & Cardin, P. Is inner core seismic anisotropy a marker for plastic flow of cubic iron? Geophys. Res. Lett. 42, 1326–1333 (2015).
Martorell, B., Brodholt, J., Wood, I. G. & Vočadlo, L. The effect of nickel on the properties of iron at the conditions of Earth’s inner core: ab initio calculations of seismic wave velocities of Fe–Ni alloys. Earth Planet. Sci. Lett. 365, 143–151 (2013).
McDonough, W. F. & Sun, S. S. The composition of the Earth. Chem. Geol. 120, 223–253 (1995).
Miyagi, L. et al. In situ phase transformation and deformation of iron at high pressure and temperature. J. Appl. Phys. 104, 103510 (2008).
Merkel, S., Gruson, M., Wang, Y., Nishiyama, N. & Tomé, C. N. Texture and elastic strains in hcp-iron plastically deformed up to 17.5 GPa and 600 K: experiment and model. Model. Simul. Mat. Sci. Eng. 20, 24005 (2012).
Frost, D. A. & Romanowicz, B. On the orientation of the fast and slow directions of anisotropy in the deep inner core. Phys. Earth Planet. Inter. 286, 101–110 (2019).
Garcia, R. & Souriau, A. Inner core anisotropy and heterogeneity level. Geophys. Res. Lett. 27, 3121–3124 (2000).
Frost, D. A. & Romanowicz, B. Constraints on inner core anisotropy using array observations of P′P′. Geophys. Res. Lett. 44, 10878–10886 (2017).
Romanowicz, B., Li, X. D. & Durek, J. Anisotropy in the inner core: could it be due to low-order convection? Science 274, 963–966 (1996).
Irving, J. C. E. & Deuss, A. Stratified anisotropic structure at the top of Earth’s inner core: a normal mode study. Phys. Earth Planet. Inter. 186, 59–69 (2011).
Bréger, L., Romanowicz, B. & Rousset, S. New constraints on the structure of the inner core from P′P′. Geophys. Res. Lett. 27, 2781–2784 (2000).
Yu, S. & Garnero, E. J. Ultralow velocity zone locations: a global assessment. Geochem. Geophys. Geosyst. 19, 396–414 (2018).
Ritterbex, S. & Tsuchiya, T. Viscosity of hcp iron at Earth’s inner core conditions from density functional theory. Sci. Rep. 10, 6311 (2020).
Torsvik, T. H., Smethurst, M. A., Burke, K. & Steinberger, B. Large igneous provinces generated from the margins of the large low-velocity provinces in the deep mantle. Geophys. J. Int. 167, 1447–1460 (2006).
Dziewonski, A. M., Lekic, V. & Romanowicz, B. A. Mantle anchor structure: an argument for bottom up tectonics. Earth Planet. Sci. Lett. 299, 69–79 (2010).
Greff-Lefftz, M. & Besse, J. Paleo movement of continents since 300 Ma, mantle dynamics and large wander of the rotational pole. Earth Planet. Sci. Lett. 345–348, 151–158 (2012).
Ballmer, M. D., Houser, C., Hernlund, J. W., Wentzcovitch, R. M. & Hirose, K. Persistence of strong silica-enriched domains in the Earth’s lower mantle. Nat. Geosci. 10, 236–240 (2017).
Aubert, J., Finlay, C. C. & Fournier, A. Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502, 219–223 (2013).
Tkalčić, H. Large variations in travel times of mantle-sensitive seismic waves from the South Sandwich Islands: is the Earth’s inner core a conglomerate of anisotropic domains? Geophys. Res. Lett. 37, L14312 (2010).
Biggin, A. J. et al. Palaeomagnetic field intensity variations suggest Mesoproterozoic inner-core nucleation. Nature 526, 245–248 (2015).
Bono, R. K., Tarduno, J. A., Nimmo, F. & Cottrell, R. D. Young inner core inferred from Ediacaran ultra-low geomagnetic field intensity. Nat. Geosci. 12, 143–147 (2019).
Irving, J. C. E. Imaging the inner core under Africa and Europe. Phys. Earth Planet. Inter. 254, 12–24 (2016).
Tkalčić, H., Romanowicz, B. & Houy, N. Constraints on D′′ structure using PKP(AB–DF), PKP(BC–DF) and PcP–P traveltime data from broad-band records. Geophys. J. Int. 148, 599–616 (2002).
Cao, A. & Romanowicz, B. Test of the innermost inner core models using broadband PKIKP travel time residuals. Geophys. Res. Lett. 34, L08303 (2007).
Romanowicz, B. et al. Seismic anisotropy in the Earth’s innermost inner core: testing structural models against mineral physics predictions. Geophys. Res. Lett. https://doi.org/10.1002/2015GL066734 (2015).
Tkalčić, H., Young, M., Muir, J. B., Davies, D. R. & Mattesini, M. Strong, multi-scale heterogeneity in Earth’s lowermost mantle. Sci. Rep. 5, 18416 (2015).
Engdahl, E. R., van der Hilst, R. & Buland, R. Global teleseismic earthquake relocation with improved travel times and procedures for depth determination. Bull. Seismol. Soc. Am. 88, 722–743 (1998).
Kennett, B. L. N., Engdahl, E. R. & Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 122, 108–124 (1995).
Kennett, B. L. N. & Gudmundsson, O. Ellipticity corrections for seismic phases. Geophys. J. Int. 127, 40–48 (1996).
Creager, K. C. Anisotropy of the inner core from differential travel times of the phases PKP and PKIKP. Nature 356, 309–314 (1992).
Yu, W. C. H. E. et al. The inner core hemispheric boundary near 180 °W. Phys. Earth Planet. Inter. 272, 1–16 (2017).
Romanowicz, B., Tkalčić, H. & Bréger, L. in Earth’s Core: Dynamics, Structure, Rotation Vol. 31 (eds Dehant, V. et al.) 31–44 (AGU, 2003).
Romanowicz, B. & Wenk, H. R. Anisotropy in the deep Earth. Phys. Earth Planet. Inter. 269, 58–90 (2017).
Frost, D. A. & Romanowicz, B. Effects of upper mantle structure beneath Alaska on core-sensitive seismic wave absolute and differential measurements: implications for estimates of inner core anisotropy. Phys. Earth Planet. Inter. 315, 106713 (2021).
Frost, D. A., Romanowicz, B. & Roecker, S. Upper mantle slab under Alaska: contribution to anomalous core-phase observations on south-Sandwich to Alaska paths. Phys. Earth Planet. Inter. 299, 106427 (2020).
Deguen, R., Olson, P. & Reynolds, E. F-layer formation in the outer core with asymmetric inner core growth. C. R. Geosci. 346, 101–109 (2014).
Lasbleis, M., Waszek, L. & Day, E. A. GrowYourIC: a step toward a coherent model of the earth’s inner core seismic structure. Geochem. Geophys. Geosyst. 18, 4016–4026 (2017).
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358 (2012).
Dobson, D. Earth’s core problem. Nature 534, 45 (2016).
Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K. & Ohishi, Y. Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 534, 95–98 (2016).
Tateno, S., Hirose, K., Ohishi, Y. & Tatsumi, Y. The structure of iron in earth’s inner core. Science 330, 359–362 (2010).
Belonoshko, A. B. et al. Stabilization of body-centred cubic iron under inner-core conditions. Nat. Geosci. 10, 312–316 (2017).
Vočadlo, L. et al. The stability of bcc-Fe at high pressures and temperatures with respect to tetragonal strain. Phys. Earth Planet. Inter. 170, 52–59 (2008).
Vočadlo, L., Dobson, D. P. & Wood, I. G. Ab initio calculations of the elasticity of hcp-Fe as a function of temperature at inner-core pressure. Earth Planet. Sci. Lett. 288, 534–538 (2009).
Martorell, B., Vocǎdlo, L., Brodholt, J. & Wood, I. G. Strong premelting effect in the elastic properties of hcp-Fe under inner-core conditions. Science 342, 466–468 (2013).
Steinle-Neumann, G., Stixrude, L., Cohen, R. E. & Gülseren, O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 413, 57–60 (2001).
Gannarelli, C. M. S., Alfè, D. & Gillan, M. J. The particle-in-cell model for ab initio thermodynamics: implications for the elastic anisotropy of the Earth’s inner core. Phys. Earth Planet. Inter. 139, 243–253 (2003).
Gannarelli, C. M. S., Alfè, D. & Gillan, M. J. The axial ratio of hcp iron at the conditions of the Earth’s inner core. Phys. Earth Planet. Inter. 152, 67–77 (2005).
Antonangeli, D., Merkel, S. & Farber, D. L. Elastic anisotropy in hcp metals at high pressure and the sound wave anisotropy of the Earth’s inner core. Geophys. Res. Lett. 33, L24303 (2006).
Martorell, B., Wood, I. G., Brodholt, J. & Vočadlo, L. The elastic properties of hcp-Fe1-xSix at Earth’s inner-core conditions. Earth Planet. Sci. Lett. 451, 89–96 (2016).
Wu, X., Mookherjee, M., Gu, T. & Qin, S. Elasticity and anisotropy of iron-nickel phosphides at high pressures. Geophys. Res. Lett. 38, 10–13 (2011).
Mookherjee, M. Elasticity and anisotropy of Fe3C at high pressures. Am. Mineral. 96, 1530–1536 (2011).
Mookherjee, M. et al. High-pressure behavior of iron carbide (Fe7C3) at inner core conditions. J. Geophys. Res. Solid Earth 116, B04201 (2011).
Li, Y., Vočadlo, L., Alfè, D. & Brodholt, J. Mg partitioning between solid and liquid iron under the Earth’s core conditions. Phys. Earth Planet. Inter. 274, 218–221 (2018).
Bergman, M. I. Measurements of electric anisotropy due to solidification texturing and the implications for the Earth’s inner core. Nature 389, 60–63 (1997).
Stacey, F. D. & Davis, P. M. High pressure equations of state with applications to the lower mantle and core. Phys. Earth Planet. Inter. 142, 137–184 (2004).
Dziewonski, A. M. & Anderson, D. L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Crotwell, H. P., Owens, T. J. & Ritsema, J. The TauP toolkit: flexible seismic travel-time and ray-path utilities. Seismol. Res. Lett. 70, 154–160 (1999).
Lasbleis, M. GrowYourIC: v0.6 (2021); https://doi.org/10.5281/zenodo.4560747
Wessel, P. et al. The generic mapping tools version 6. Geochem. Geophys. Geosyst. 20, 5556–5564 (2019).
Waszek, L., Irving, J. & Deuss, A. Reconciling the hemispherical structure of Earth’s inner core with its super-rotation. Nat. Geosci. 4, 264–267 (2011).
Acknowledgements
The authors acknowledge the following funding sources: National Science Foundation grants EAR-1135452 and EAR-1829283 to D.A.F. and B.R.; the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 795289 to M.L.; and National Science Foundation grant EAR 1343908 and US Department of Energy grant DE-FG02-05ER15637 to B.C.
Author information
Authors and Affiliations
Contributions
All authors contributed to project design, methodology development, model conceptualization and manuscript preparation. D.A.F. was responsible for seismic data curation and formal analysis and wrote the first draft of the paper. M.L. contributed to the geodynamic modelling and B.C. provided the mineral physics input. D.A.F. and B.R. coordinated the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Geoscience thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Stefan Lachowycz.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Distribution of sources of receivers.
Locations of sources (circles) and receivers (triangles) used in this study. Stations with newly acquired data are shown in cyan.
Extended Data Fig. 2 Measuring PKP differential travel times.
Example waveforms of (left) PKPdf and (right) PKPab for a M6.0 event in Baffin Bay on 2009/07/07 observed at station P124 in Antarctica. Waveforms are aligned on the predicted arrival time of the respective phases. Waveforms are shown as (a–c) broadly filtered at 0.03–2 Hz, (b–d) narrowly filtered at 0.4–2.0 Hz. In (c) and (d) waveforms have been Hilbert transformed. Measured arrival times are shown as red lines. Predicted arrivals (in model ak135 with ellipticity corrections) are shown by black solid and dashed lines for direct and depth phases, respectively.
Extended Data Fig. 3 Differential travel times as a function of angle to the rotation axis, ξ, and depth.
PKPbc-df and PKPab-df travel time anomalies and effective velocity anomalies (excluding the data recorded at stations in Alaska) as a function of angle ξ with respect to the rotation axis, separated by ray turning depth for (a, b, and c) ICB to 5600 km, (d, e, and f) 5600 km to 6000 km, and (g, h, and i) 6000 km to Earth’s centre. (a, d, g): All travel time anomalies. (b, e, h) Travel time anomalies split into data turning in the western (red) and eastern (blue) hemispheres. (c, f, i) Effective velocity anomalies in the IC split by hemisphere. The WH western boundary is set at 159° W, and the WH eastern boundary is set at 40° E, as explained in Extended Data Figure 4.
Extended Data Fig. 4 Locating the western boundary of the western hemisphere.
Best fit of WH western boundary locations calculated using polar data (ξ < 15°) and excluding data from stations in Alaska. Black solid line marks the R2 fit and red region describes the region of highest R2, most likely containing the location of the boundary, which runs between 166° W and 159° W. R2 drops sharply at < 166° W and >153° W. Black dashed line and grey shading show the mean and standard deviation of R2 values for 200 bootstrap resamples. The eastern boundary is fixed at 40°E, following the result of Irving (2016). Western boundary locations from previous studies are marked in blue: Tanaka & Hamaguchi 19976; Creager 19997; Waszek et al. 201178; Irving & Deuss 20118; while that of Lythgoe et al. 20149 plots outside of the region shown.
Extended Data Fig. 5 Pattern of effective velocity anomaly with depth.
Effective velocity anomaly in the IC as a function of epicentral distance for ξ in the range (a and c) 0 to 30°, and (b and d) 0 to 15°. Left panels show data coloured by ξ, and right panels show data split into those turning in the eastern (blue) and western (red) hemispheres. The western hemisphere is defined as between 159° W and 40° E, as explained in Extended Data Figure 4. The linear trend with distance, solid line, is particularly clear for the most polar data (c and f), indicating increasing anisotropy with depth.
Extended Data Fig. 6 Distribution of slow axes of anisotropy.
Slow directions of anisotropy in our final model (Fig. 3), measured relative to the rotation (N-S) axis in the (a) plane perpendicular to the direction of translation (blue arrow coming out of plane), and (b) plane parallel to the direction of translation (blue arrow) from the left (east) to right (west) of the figure, respectively.
Extended Data Fig.7 Predicted versus observed PKP velocity anomalies for pure hcp Fe.
Predicted (dark blue and red dots and with mean as grey squares) and observed (light blue and orange dots and with mean as black diamonds) effective velocity anomalies as a function of (a) epicentral distance for data with ξ ≤ 15°, marked by dashed line in b and c, and as a function of ξ in the (b) western and (c) eastern hemispheres. Error bars for the data show the mean and one standard deviation at 2.5° and 5° increments for panels a, and b and c, respectively. We use the elastic tensor for pure HCP Fe at 5500 K and 360 GPa67, an age of 0.5 Ga, and a translation rate of 0.3 radii over the age of the IC. Variance reduction for the data with ξ < 15° is 73% compared to 93% for our model with Fe93.25Ni6.75.
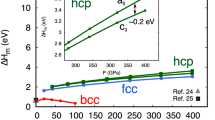
Extended Data Fig. 8 The effect of pressure on anisotropy.
(a) Elastic constants for hcp iron as a function of pressure calculated from the reference position at 360 GPa and 5500 K, extrapolated using results from several calculations67,61 at 5500 K and 316 GPa, and 5500 K and 360 GPa. (b) Resultant anisotropy across the pressure range of the inner core. Direction of minimum velocity anomaly is marked by black circles. The orientation of the minimum anisotropy moves towards higher ξ values (more equatorial) with increasing pressure.
Extended Data Fig. 9 Differential travel time anomalies for western hemisphere data turning within 450 km of the ICB with respect to model ak135, as a function of angle to the rotation axis, ξ.
Travel time anomalies of (a) PKPbc-df and (b) PKPac-df phase pairs showing that observations at stations in Alaska (green) do not fit the global pattern, while observations from sources in Alaska (purple) do. Anisotropy curves are calculated using equation. S1, assuming constant cylindrical anisotropy through the inner core, for all data (green curve) and all data except that recorded in Alaska (blue curve).
Supplementary information
Supplementary Information
Supplementary Figs. 1 and 2.
Supplementary Data 1
Travel-time picks measured in this study.
Rights and permissions
About this article
Cite this article
Frost, D.A., Lasbleis, M., Chandler, B. et al. Dynamic history of the inner core constrained by seismic anisotropy. Nat. Geosci. 14, 531–535 (2021). https://doi.org/10.1038/s41561-021-00761-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-021-00761-w
This article is cited by
-
Superionic effect and anisotropic texture in Earth’s inner core driven by geomagnetic field
Nature Communications (2023)
-
Up-to-fivefold reverberating waves through the Earth’s center and distinctly anisotropic innermost inner core
Nature Communications (2023)
-
Seismic insights into Earth’s core
Nature Communications (2023)
-
An initial map of fine-scale heterogeneity in the Earth’s inner core
Nature Geoscience (2022)
-
Early Cambrian renewal of the geodynamo and the origin of inner core structure
Nature Communications (2022)