Abstract
Water ice becomes a superionic phase under the high pressure and temperature conditions of deep planetary interiors of ice planets such as Neptune and Uranus, which affects interior structures and generates magnetic fields. The solid Earth, however, contains only hydrous minerals with a negligible amount of ice. Here we combine high pressure and temperature electrical conductivity experiments, Raman spectroscopy and first-principles simulations to investigate the state of hydrogen in the pyrite-type FeO2Hx (x ≤ 1), which is a potential H-bearing phase near the core–mantle boundary. We find that when the pressure increases beyond 73 GPa at room temperature, symmetric hydroxyl bonds are softened and the H+ (or proton) becomes diffusive within the vicinity of its crystallographic site. Increasing temperature under pressure, the diffusivity of hydrogen is extended beyond the individual unit cell to cover the entire solid, and the electrical conductivity soars, indicating a transition to the superionic state, which is characterized by freely moving protons and a solid FeO2 lattice. The highly diffusive hydrogen provides fresh transport mechanisms for charge and mass, which dictate the geophysical behaviours of electrical conductivity and magnetism, as well as geochemical processes of redox, hydrogen circulation and hydrogen isotopic mixing in Earth’s deep mantle.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data supporting the findings of this study have been deposited at the 4TU Center for Research Data (https://doi.org/10.4121/13487643.v1). Any additional data can be requested by e-mailing the corresponding author. Source data are provided with this paper.
Code availability
The Vienna Ab Initio Simulation Package is a proprietary software available for purchase at https://www.vasp.at/. CP2K is freely available under the GPL license at https://www.cp2k.org/. Peakfit is available for purchase at https://systatsoftware.com/products/peakfit/.
References
Pamato, M. G. et al. Lower-mantle water reservoir implied by the extreme stability of a hydrous aluminosilicate. Nat. Geosci. 8, 75–79 (2014).
Schmandt, B., Jacobsen, S. D., Becker, T. W., Liu, Z. & Dueker, K. G. Dehydration melting at the top of the lower mantle. Science 344, 1265–1268 (2014).
Wang, D., Mookherjee, M., Xu, Y. & Karato, S.-I. The effect of water on the electrical conductivity of olivine. Nature 443, 977–980 (2006).
Yoshino, T. & Katsura, T. Electrical conductivity of mantle minerals: role of water in conductivity anomalies. Annu. Rev. Earth Planet. Sci. 41, 605–628 (2013).
Chang, Y.-Y., Hsieh, W.-P., Tan, E. & Chen, J. Hydration-reduced lattice thermal conductivity of olivine in Earth’s upper mantle. Proc. Natl Acad. Sci. USA 114, 4078–4081 (2017).
Mao, Z. et al. Velocity crossover between hydrous and anhydrous forsterite at high pressures. Earth Planet. Sci. Lett. 293, 250–258 (2010).
Litasov, K. D. & Ohtani, E. in Advances in High-Pressure Mineralogy Special Paper 421 (ed. Ohtani, E.) 115–156 (Geological Society of America, 2007).
Hirschmann, M. M. Water, melting, and the deep Earth H2O cycle. Annu. Rev. Earth Planet. Sci. 34, 629–653 (2006).
Jacobsen, S. D. & van der Lee, S. Earth’s Deep Water Cycle Volume 168 (American Geophysical Union, 2006).
Ni, H. et al. Distribution, cycling and impact of water in the Earth’s interior. Natl Sci. Rev. 4, 879–891 (2017).
Goncharov, A. F., Struzhkin, V. V., Somayazulu, M., Hemley, R. J. & Mao, H. K. Compression of ice to 210 GPa: evidence for a symmetric hydrogen bonded phase. Science 273, 218–220 (1996).
Cavazzoni, C. et al. Superionic and metallic states of water and ammonia at giant planet conditions. Science 283, 44–46 (1999).
Sugimura, E. et al. Experimental evidence of superionic conduction in H2O ice. J. Chem. Phys. 137, 194505 (2012).
Millot, M. et al. Experimental evidence for superionic water ice using shock compression. Nat. Phys. 14, 297–302 (2018).
Millot, M. et al. Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 569, 251–255 (2019).
Hu, Q. et al. Dehydrogenation of goethite in Earth’s deep lower mantle. Proc. Natl Acad. Sci. USA 114, 1498–1501 (2017).
Nishi, M., Kuwayama, Y., Tsuchiya, J. & Tsuchiya, T. The pyrite-type high-pressure form of FeOOH. Nature 547, 205–208 (2017).
Boulard, E. et al. CO2-induced destabilization of pyrite-structured FeO2Hx in the lower mantle. Natl Sci. Rev. 5, 870–877 (2018).
Yuan, L. et al. Chemical reactions between Fe and H2O up to megabar pressures and implications for water storage in the Earth’s mantle and core. Geophys. Res. Lett. 45, 1330–1338 (2018).
Hernandez, J.-A. & Caracas, R. Superionic–superionic phase transitions in body-centered cubic H2O ice. Phys. Rev. Lett. 117, 135503 (2016).
Futera, Z., Tse, J. S. & English, N. J. Possibility of realizing superionic ice VII in external electric fields of planetary bodies. Sci. Adv. 6, eaaz2915 (2020).
Ohta, K. et al. The electrical conductivity of post-perovskite in Earth’s D” layer. Science 320, 89–91 (2008).
Sinmyo, R., Pesce, G., Greenberg, E., McCammon, C. & Dubrovinsky, L. Lower mantle electrical conductivity based on measurements of Al, Fe-bearing perovskite under lower mantle conditions. Earth Planet. Sci. Lett. 393, 165–172 (2014).
Ohta, K., Yagi, T., Hirose, K. & Ohishi, Y. Thermal conductivity of ferropericlase in the Earth’s lower mantle. Earth Planet. Sci. Lett. 465, 29–37 (2017).
Zhang, Y. et al. Reconciliation of experiments and theory on transport properties of iron and the geodynamo. Phys. Rev. Lett. 125, 078501 (2020).
Mao, H.-K. et al. When water meets iron at Earth’s core–mantle boundary. Natl Sci. Rev. 4, 870–878 (2017).
Khan, A. & Shankland, T. J. A geophysical perspective on mantle water content and melting: inverting electromagnetic sounding data using laboratory-based electrical conductivity profiles. Earth Planet. Sci. Lett. 317–318, 27–43 (2012).
Deschamps, F. & Khan, A. Electrical conductivity as a constraint on lower mantle thermo-chemical structure. Earth Planet. Sci. Lett. 450, 108–119 (2016).
Liu, J. et al. Hydrogen-bearing iron peroxide and the origin of ultralow-velocity zones. Nature 551, 494–497 (2017).
Hsieh, W.-P., Deschamps, F., Okuchi, T. & Lin, J.-F. Effects of iron on the lattice thermal conductivity of Earth’s deep mantle and implications for mantle dynamics. Proc. Natl Acad. Sci. USA 115, 4099–4104 (2018).
Liu, J. et al. Altered chemistry of oxygen and iron under deep Earth conditions. Nat. Commun. 10, 153 (2019).
McCammon, C. The paradox of mantle redox. Science 308, 807–808 (2005).
Stagno, V., Ojwang, D. O., McCammon, C. A. & Frost, D. J. The oxidation state of the mantle and the extraction of carbon from Earth’s interior. Nature 493, 84–88 (2013).
Clog, M., Auband, C., Cartigny, P. & Dosso, L. The hydrogen isotopic compositions and water content of southern Pacific MORB: a reassessment of D/H ratio of the depleted mantle reservior. Earth Planet. Sci. Lett. 381, 156–165 (2013).
Boulard, E. et al. Ferrous iron under oxygen-rich conditions in the deep mantle. Geophys. Res. Lett. 46, 1348–1356 (2019).
Yoshino, T., Baker, E. & Duffey, K. Fate of water in subducted hydrous sediments deduced from stability fields of FeOOH and AlOOH up to 20 GPa. Phys. Earth Planet. Inter. 294, 106295 (2019).
Struzhkin, V. et al. Superconductivity in La and Y hydrides: remaining questions to experiment and theory. Matter Radiat. Extremes 5, 028201 (2020).
Snider, E. et al. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature 586, 373–377 (2020).
Eremets, M. I., Drozdov, A. P., Kong, P. P. & Wang, H. Semimetallic molecular hydrogen at pressure above 350 GPa. Nat. Phys. 15, 1246–1249 (2019).
Ji, C. et al. Crystallography of low Z material at ultrahigh pressure: case study on solid hydrogen. Matter Radiat. Extremes 5, 038401 (2020).
Gregoryanz, E. et al. Everything you always wanted to know about metallic hydrogen but were afraid to ask. Matter Radiat. Extremes 5, 038101 (2020).
Weir, S. T., Mitchell, A. C. & Nellis, W. J. Metallization of fluid molecular hydrogen at 140 GPa (1.4 Mbar). Phys. Rev. Lett. 76, 1860–1863 (1996).
Ohta, K. et al. Electrical conductivities of pyrolitic mantle and MORB materials up to the lowermost mantle conditions. Earth Planet. Sci. Lett. 289, 497–502 (2010).
Ohta, K. et al. Experimental and theoretical evidence for pressure-induced metallization in FeO with rocksalt-type structure. Phys. Rev. Lett. 108, 026403 (2012).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984).
Dickey, J. M. & Paskin, A. Computer simulation of the lattice dynamics of solids. Phys. Rev. 188, 1407–1418 (1969).
French, M., Hamel, S. & Redmer, R. Dynamical screening and ionic conductivity in water from ab initio simulations. Phys. Rev. Lett. 107, 185901 (2011).
Hutter, J., Iannuzzi, M., Schiffmann, F. & VandeVondele, J. cp2k: atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 4, 15–25 (2014).
Goedecker, S., Teter, M. & Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 54, 1703–1710 (1996).
Ceriotti, M., Bussi, G. & Parrinello, M. Colored-noise thermostats à la carte. J. Chem. Theory Comput. 6, 1170–1180 (2010).
Umari, P. & Pasquarello, A. Ab initio molecular dynamics in a finite homogeneous electric field. Phys. Rev. Lett. 89, 157602 (2002).
Cassone, G., Giaquinta, P. V., Saija, F. & Saitta, A. M. Effect of electric field orientation on the mechanical and electrical properties of water ices: an ab-initio study. J. Phys. Chem. B 118, 12717–12724 (2014).
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358 (2012).
de Koker, N., Steinle-Neumann, G. & Vlček, V. Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth’s core. Proc. Natl Acad. Sci. USA 109, 4070–4073 (2012).
Di Paola, C., Macheda, F., Laricchia, S., Weber, C. & Bonini, N. First-principles study of electronic transport and structural properties of Cu12Sb4S13 in its high-temperature phase. Phys. Rev. Res. 2, 033055 (2020).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Haule, K. & Birol, T. Free energy from stationary implementation of the DFT+DMFT functional. Phys. Rev. Lett. 115, 256402 (2015).
Xu, J. et al. Thermal conductivity and electrical resistivity of solid iron at Earth’s core conditions from first principles. Phys. Rev. Lett. 121, 096601 (2018).
Hausoel, A. et al. Local magnetic moments in iron and nickel at ambient and Earth’s core conditions. Nat. Commun. 8, 16062 (2017).
Prakapenka, V. B. et al. Advanced flat top laser heating system for high pressure research at GSECARS: application to the melting behavior of germanium. High Press. Res. 28, 225–235 (2008).
Shen, G., Rivers, M. L., Wang, Y. & Sutton, S. R. Laser heated diamond cell system at the Advanced Photon Source for in situ X-ray measurements at high pressure and temperature. Rev. Sci. Instrum. 72, 1273–1282 (2001).
Holtgrewe, N., Greenberg, E., Prescher, C., Prakapenka, V. B. & Goncharov, A. F. Advanced integrated optical spectroscopy system for diamond anvil cell studies at GSECARS. High. Press. Res. 39, 457–470 (2019).
Akahama, Y. & Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 310GPa. J. Appl. Phys. 100, 043516 (2006).
Buehler, M. G. & Thurber, W. R. An experimental study of various cross sheet resistor test structures. J. Electrochem. Soc. 125, 645–650 (1978).
Acknowledgements
Y.H. is also supported by HPSTAR. We acknowledge X. Du, N. Li, Y. Zhao, W. Yang and E. Greenburg for assistance in conducting laser heating and EC measurements; J. Cheng and B. Li for conducting Raman; and Y. Sun for FPMD technical support. This work is supported by the National Key Research and Development Program of China (2019YFA0708502), the National Natural Science Foundation of China (grant no. U1530402, U1930401, 41774101 and 11774015) and the Youth Innovation Promotion Association of CAS (2020394). XRD patterns were collected at High Pressure Collaborative Access Team (16ID-B) and GeoSoilEnviroCARS (13ID-D), Advanced Photon Source (APS), Argonne National Laboratory. HPCAT operations are supported by DOE-NNSA’s Office of Experimental Sciences. APS is supported by DOE-BES, under contract no. DE-AC02-06CH11357. GeoSoilEnviroCARS is supported by the National Science Foundation—Earth Sciences (EAR - 1634415) and Department of Energy—Geosciences (DE-FG02-94ER14466). M.H. is supported by NSF grant EAR-1847707. Y.Z. is supported by China Postdoctoral Science Foundation grant 18NZ021-0213-216308. J.C. acknowledges the support of NSF grant EAR-1723185. L.D. is supportd by the Strategic Priority Research Program of CAS under grant XDB18000000. J.H.S. is supported by the Brain Pool Program through the National Research Foundation of Korea funded by the Ministry of Science and ICT under grant NRF-2020H1D3A2A02111022. C.J.P. is supported by a Royal Society Wolfson Research Merit Award. R.J.N. is supported by the Engineering and Physical Sciences Research Council under the grant EP/P034616/1. H.-K.M. is supported by NSF grants EAR-1722515 and EAR-1447438. Q.H. is supported by a Tencent XPLORER Prize.
Author information
Authors and Affiliations
Contributions
Q.H., D.Y.K. and H.-K.M. formulated the concept of the study. Y.H., Q.H., B.G.J., J.H.S., D.Y.K., S.S., C.J.P. and R.J.N. conducted the theoretical simulation. M.H., Y.Z., L.D., F.K., B.C., J.L. and Q.H. performed electrical conductivity measurements. Q.H. carried out the Raman. J.L., Q.H., R.T., J.C., Y.M. and V.B.P. performed the XRD experiment. M.H., Y.H. and Q.H. performed the data analysis. Q.H., H.-K.M, M.H., Y.H. and J.L. wrote the manuscript with contributions from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Geoscience thanks Jean-Alexis Hernandez and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Rebecca Neely.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Volumes of Py-FeO2 and Py-FeO2Hx under pressure and room temperature.
Open circles are experimental volumes in literature. Measurement uncertainties from XRD are generally less than the symbol size. Dash curves are volumes of FeO2Hx with x=0, 0.25, 0.5, 0.75 and 1.0 from theoretical calculation (see Methods). The stability and stoichiometry of FeO2-FeO2H in pyrite structure. In eight different experiments converting FeO2H to the Py-phase at 86.0–133.5 GPa and 1500–2500 K, Hu et al. observed a wide variation of the unit-cell volume, that was attributed to the variation of x from 0.43 to 0.81 in Py-FeO2Hx due to the difference in the P–T of their synthesis. The set of curves for the volume dependence on x and P as shown in Fig. S1. Nishi. et al. conducted a set of experiments with all P–V data correspond to the maximum of Hu’s volume. Subsequent investigations by Yuan et al. from Tohoku University synthesized a Py-FeO2Hx with unit-cell volumes 2% larger than Nishi. et al. approaching the full hydrogenation of x = 1. Many additional publications in 2017–2019 further showed variation of volume and thus H. Most importantly, all experiments of four different groups consistently demonstrated that Py-FeO2Hx (x≤1) is stable under DLM pressures and is at least thermodynamically stable up to 2500–2600 K at 110 GPa. While the exact stoichiometry of the H and its relation to P, T, and hydrogen fugacity remain interesting, it is not the subject of the present work which focuses on the superionization behavior in hydrogen in the Py phase regardless of its stoichiometry. Therefore, our FPMD simulation chose x = 0.5 and 1.0 because they mainly cover the range of x obtained from XRD experiments.
Extended Data Fig. 2 Covalent to ionic bonding transition.
a, The evolution of RO-H as a function of O-O distance RO-O. Magenta triangles: α-FeOOH; green squares: ε-FeOOH; red circles: pyrite FeO2H; orange inverted triangles: δ-AlOOH (Tsuchiya, Geophys. Res. Lett. 2002); cyan stars: Phase D (MgSi2O2H, Tsuchiya, Am. Mineral. 2005); grey diamonds: ice (VII to X) at 100 K simulated by M. Benoit et al. (Benoit, Nature 1998); purple solid line: line with symmetric O-H-O bonds (RO-H = RO-O/2). The lower panel is the electron localization function (ELF) distributions viewed along [001] direction for ε-FeOOH and [111] direction for Py-FeO2H. Yellow, white, and red spheres represent Fe, H and O atoms, respectively. Once synthesized at high pressure, the Py-FeO2Hx already features symmetric O-H-O bonding (Gleason Earth Planet. Sci. Lett. 2013). The change of RO-H/RO-O pairs indicated the delocalization of H between the two O atoms in both ε-FeOOH and Py-FeO2H when pressure raised above 50 GPa. b, Distribution of Electron localization function. H in the symmetric bonding partially loss its electrons and form a stronger ionic bond with O atoms. The stiffen of O-H-O bonds results in the blueshifts of hydroxyl Raman peaks (Fig. 2). c, Calculated VDOS of FeO2H at 300 K and pressures of 68.9 (black curve), 93.1 (red curve), and 114.8 GPa (blue curve). The movement of vibration modes is consistent with experiment.
Extended Data Fig. 3 The evolution of MSDs, trajectories and melting of FeO2H0.5.
Black, red and blue curves represent MSDs of H, Fe and O ions in FeO2H0.5. a, Ordinary solid FeO2Hx. b, The skyrocketing MSD of hydrogen indicate the onset of superionic state in Fig. 1. Uncertainties of pressure and temperature are sampled from the trajectories. c, Calculated melting temperature using Z method. The open circles show the pressures and temperatures of our simulations. The connection of these circles presents a shape like letter Z. The transition from the solid superheating state to liquid state is pointed out with arrows.
Extended Data Fig. 4 Proton diffusion coefficients of superionic Py-FeO2H and Py-FeO2H0.5.
a, Black, red, blue and green symbols represent proton diffusion coefficients of FeO2H at 80 GPa, FeO2H at 130 GPa, FeO2H0.5 at 80 GPa and FeO2H0.5 at 130 GPa, respectively. b, The localized superionic phase with protons distributed between two nearby O ions. c, The delocalized superionic phase with protons delocalizing from O-H-O triplet. Small grey and pink spheres denote the trajectories of the H and O ions, respectively. The intermediate phase was previously studied by Hernandez and Caracas in ice as ice phase VII”. Protons in ice VII” delocalize from the O-H-O triplet and become even more diffusive. The intermediate phase may explain the further raising of the EC in Py-FeO2Hx above ~2000 K and 121 GPa. We have been inspired to conducted FPMD simulations and have also observed the delocalized phase in Py-FeO2H at temperatures above 3000 K. We compared the trajectories of H and O ions at 2000 and 3000 K in FeO2H. At 2000 K, the protons are mostly distributed between two nearby O ions, and they diffuse in the lattice by hopping between two symmetrized hydrogen sites. At 3300 K, movement of protons no longer binds to the nearest O atoms but travels to any possible interstitial sites in the entire lattice. The greater movement of protons can be described by the delocalized superionic phase. Similar to ice VII”, this intermediate phase helps to raise the ionic conductivity from the order of 101-102 to above 103 S m−1 and becomes visible in EC experiments.
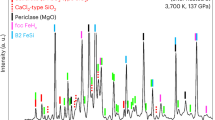
Extended Data Fig. 5 X-ray diffraction pattern of FeO2Hx at 113 GPa and quenched from 2000 K.
Pressure is measured using the equation of state of Pt. The sample completely transformed into the Py-FeO2Hx phase. The top panel is an integrated pattern from the 2D unrolled x-ray diffraction pattern at the bottom. The wavelength of the x-rays is 0.4066 Å. The strong diffraction peaks from the Py-phase confirmed that the majority of the sample is Py-FeO2Hx. The lattice parameter of the Py-phase is a = 4.392 Å, standing for x = 0.87(8) from ref. 16. The remaining diffraction peaks could be indexed to the pressure medium (LiF) and very tiny amounts of ε-FeOOH. After heating, the pressure was equilibrated at 113 GPa and the electrical leads were checked by immersing the DAC into a liquid nitrogen cryostat. The slope of the temperature versus EC plot was positive, clearly showing four electrodes were safely connected to the non-metallic sample without a short circuit (Extended Data Fig. 9).
Extended Data Fig. 6 X-ray diffraction pattern of FeO2Hx at 121 GPa and quenched from 3000–3400 K.
In the left panel, the pattern taken at the center of heating is still dominated by the Py-phase with lattice parameter a = 4.379 Å and corresponding x = 0.86(8) (ref. 16). The minor peaks in the pattern may associate with dhcp-FeHx and/or Cmcm-type Fe2O3. The reference lattices parameters are dhcp-FeHx (a = 2.458 Å, c = 8.046 Å); Cmcm-type Fe2O3 (a = 2.559 Å, a = 8.257 Å, c = 6.164 Å). Pressure is measured by the equation of state of Pt. The wavelength of the x-ray is 0.3344 Å. The right panel is an XRD mapping contour around the heating area. We first divided the heated portion of sample into (21 × 21 μm2) a 7 × 7 matrix. We collect one XRD pattern on each grid point with the same 10-seconds’ exposure time. Colors on the color bar are proportional to the intensity of Py-phase 111 peak. The contour is then constructed by interpolating those intensities.
Extended Data Fig. 7 Electrical conductivities of superionic ice from experiments and simulations.
The calculated proton conductivities of superionic ice under the P–T conditions shown in the previous figure are compared with previous experimental (Yakushenv J. Exp. Theor., 2000 and Chau J. Chem. Phys., 2001) and simulations (French, Phys. Rev. Lett. 2011).
Extended Data Fig. 8 Image of x-ray absorption for the sample with four Pt electrodes.
The sample was sandwiched by two LiF layers acting as the pressure medium and thermal isolation. Cubic-BN was used as the electrical isolator. In left panel, the shaded area corresponds to the actual sample, whose geometry was later used to determine electric conductivity. The mapping image of the x-ray absorption showed that the samples were individually connected by four Pt electrodes. The inset is the corresponding microscopic image of the sample assembly. The right panel shows the x-ray absorption along the radial side of diamond anvil cell (perpendicular to the compression axis) to access the thickness of the sample. We took this figure in a separate experiment with LiF as the pressure medium and cubic-BN isolation. Unlike the EC experiment, we used a Be gasket such that it is transparent to x-ray. The image was taken at 110 GPa after laser heating at 2000 K for 45 minutes. The directly measured thickness of 4.8 μm is consistent with the one we calibrated in EC run (4.5 μm, 113 GPa). Here, we estimate 7% of uncertainty derived from the thickness difference in these two approaches.
Extended Data Fig. 9 Temperature versus resistance for the FeO2Hx sample at 113 GPa.
The negative T-R slope indicates that the sample is an insulator. Data points were collected every 1 second. The process of warming up from 80 K to room temperature took around 60 minutes. Systematic error for resistance is less than 10−3 Ω. We estimated 5% error in temperature, due to the temperature gradient from the thermal couple to the sample. We conducted cryogenic experiments and measured the electric conductivity of FeO2Hx synthesized at 113 GPa. The purpose of cryogenic experiments is two-folded. First, we attempted to clarify whether FeO2Hx is an insulator or a conductor at room temperature. Secondly, we check the connection of 4-electrode system. It is also known that compression shrinks the available space in the sample chamber. In the worst-case scenario, it might squeeze the electrodes and shorts the circuit. This would lead to a fake metallized loop. In our cryogenic experiments, the insulating nature of the sample eliminates the possibility of electrode contact contamination. These observations secured our measurements taken for the sample instead of touching the platinum electrodes. The appearance of insulating FeO2Hx would guarantee that the van der Pauw four probe system was working. Compared with laser-heated measurements, data points collected in cryogenic experiments were controlled by a cryogenic cooling system. Two thermal couples were attached to the exterior of the diamond anvil cell and the cell was immersed in a liquid nitrogen box. The temperature was completely equilibrated around 80 K, before we removed the liquid nitrogen. The cell slowly warmed up while we measured the resistance (R) from the sample at every second. According to lattice thermal expansion of the sample, sample pressure in the cryogenic cycle is 113 ± 5 GPa.
Source data
Source Data Fig. 1
Excel file layout of P–T conditions of solid or superionic FeO2Hx.
Source Data Fig. 2
Raman spectra in Fig. 2a.
Source Data Fig. 3
Excel file layout of electrical conductivities from experiment and simulation.
Source Data Extended Data Fig. 1
Excel file layout of calculated volumes of FeO2Hx with x = 0, 0.25, 0.5, 0.75 and 1.
Source Data Extended Data Fig. 2
Excel file layout of the evolution of O–H bond length and vibrational density of states in the figure.
Source Data Extended Data Fig. 3
Excel file layout of mean-squared displacement and P–T relation from FPMD simulation.
Source Data Extended Data Fig. 4
Excel file layout of diffusion coefficients at various pressures and stoichiometries.
Source Data Extended Data Fig. 5
X-y column data for XRD spectra at 113 GPa at initial synthesis.
Source Data Extended Data Fig. 6
X-y column data for XRD spectra at 121 GPa after EC run.
Source Data Extended Data Fig. 7
Excel file layout of calculated EC of superionic ice at 140 GPa.
Source Data Extended Data Fig. 9
Temperature versus resistance in a cryogenic tank.
Rights and permissions
About this article
Cite this article
Hou, M., He, Y., Jang, B.G. et al. Superionic iron oxide–hydroxide in Earth’s deep mantle. Nat. Geosci. 14, 174–178 (2021). https://doi.org/10.1038/s41561-021-00696-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-021-00696-2
This article is cited by
-
Links between large igneous province volcanism and subducted iron formations
Nature Geoscience (2023)
-
Double superionicity in icy compounds at planetary interior conditions
Nature Communications (2023)
-
Superionic effect and anisotropic texture in Earth’s inner core driven by geomagnetic field
Nature Communications (2023)
-
Superionic iron alloys and their seismic velocities in Earth’s inner core
Nature (2022)
-
Deep Earth bound by water
Nature Geoscience (2022)