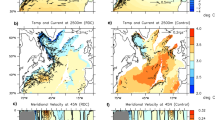
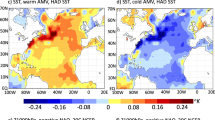
Abstract
The North Atlantic Oscillation is the dominant mode of variability of atmospheric circulation outside of the tropics in the Northern Hemisphere in winter. To understand and attribute this mode of variability is of great societal relevance for populated regions in Eurasia. It has been widely claimed that there is a robust signal of the nearly periodic 11-year solar cycle in the North Atlantic Oscillation in winter, which thereby raises the possibility of using the solar cycle to predict the circulation years in advance. Here we present evidence that contradicts this claim. First, we show the absence of a solar signal in the North Atlantic Oscillation in the instrumental record prior to the mid-1960s, and a marginally significant signal thereafter. Second, from our analysis of a global chemistry–climate model repeatedly forced with the sequence of solar irradiance since the mid-1960s, we suggest that the solar signal over this period might have been a chance occurrence due to internal variability, and hence does not imply enhanced predictability.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Code availability
The source code of the WACCM model is part of the Community Earth System Model version 1.2.0, which is publicly distributed and can be obtained after registration at www.cesm.ucar.edu/models/cesm1.2/. All the figures were produced with Matlab, version R2017a, available at www.mathworks.com. The algorithm used to perform regression, PCA and wavelet analysis was written using built-in functions from the same Matlab distribution. More specifically, regression analysis is based on the regstats function (www.mathworks.com/help/stats/regstats.html), the wavelets on the CWT function (www.mathworks.com/help/wavelet/ref/cwt.html) and the PCA on the SVD function (www.mathworks.com/help/matlab/ref/svd.html).
Data availability
HadSLP, NOAA and 20th Century reconstructions data were provided by the NOAA/OAR/ESRL PSD from their website at www.esrl.noaa.gov/psd/. ERA20 data were provided by ECMWF from their website at www.ecmwf.int/en/forecasts/datasets/archive-datasets/reanalysis-datasets/era-20c. The SSU data are available at www.remss.com/measurements/upper-air-temperature/. The CanESM2 model data are available at http://climate-modelling.canada.ca/climatemodeldata/cgcm4/CanESM2/esmControl/index.shtml. The LENS-CAM5 model data are available through the Climate Data Gateway, hosted at NCAR and are accessible at www.earthsystemgrid.org/dataset/ucar.cgd.ccsm4.output.html. Finally, the WACCM model data are stored and available in the HPSS archive on the NCAR’s Computational and Information Systems Lab, located at www2.cisl.ucar.edu/resources/storage-and-file-systems/hpss/access.
References
Barnston, A. G. & Livezey, R. E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 115, 1083–1126 (1987).
Hurrell, J. W. Decadal trends in the North Atlantic Oscillation: regional temperatures and precipitation. Science 269, 676–679 (1995).
Ineson, S. et al. Solar forcing of winter climate variability in the Northern Hemisphere. Nat. Geosci. 4, 753–757 (2011).
Gray, L. J. et al. A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. 118, 13405–13420 (2013).
Scaife, A. A. et al. A mechanism for lagged North Atlantic climate response to solar variability. Geophys. Res. Lett. 40, 434–439 (2013).
Andrews, M., Knight, J. & Gray, L. A simulated lagged response of the North Atlantic Oscillation to the solar cycle over the period 1960–2009. Env. Res. Lett. 10, L054022 (2015).
Gray, L., Woollings, T., Andrews, M. & Knight, J. Eleven-year solar cycle signal in the NAO and Atlantic/European blocking. Q. J. R. Meteorol. Soc. 142, 1890–1903 (2016).
Scaife, A. et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 41, 2514–2519 (2014).
Haigh, J. D. The impact of solar variability on climate. Science 272, 981–984 (1996).
Kodera, K. & Kuroda, Y. Dynamical response to the solar cycle. J. Geophys. Res. 107, 4749 (2002).
Matthes, K., Kuroda, Y., Kodera, K. & Langematz, U. Transfer of the solar signal from the stratosphere to the troposphere: northern winter. J. Geophys. Res. 111, D06108 (2006).
Chiodo, G., Calvo, N., Marsh, D. & Garcia-Herrera, R. The 11 year solar cycle signal in transient simulations from the whole atmosphere community climate model. J. Geophys. Res. 117, D06109 (2012).
Gerber, E. P. & Polvani, L. M. Stratosphere–troposphere coupling in a relatively simple AGCM: the importance of stratospheric variability. J. Clim. 22, 1920–1933 (2009).
Thiéblemont, R., Matthes, K., Omrani, N.-E., Kodera, K. & Hansen, F. Solar forcing synchronizes decadal North Atlantic climate variability. Nat. Commun. 6, 8268 (2015).
Siscoe, G. L. Solar-terrestrial influences on weather and climate. Nature 276, 348–352 (1978).
Baldwin, M. & Dunkerton, T. Observations and statistical simulations of a proposed solar cycle/QBO/weather relationship. Geophys. Res. Lett. 16, 863–866 (1989).
Pittock, B. Can solar variations explain variations in the Earth’s climate? Clim. Change 96, 483–487 (2009).
Turner, T. E. et al. Solar cycles or random processes? Evaluating solar variability in Holocene climate records. Sci. Rep. 6, 23961 (2016).
Van Loon, H. & Meehl, G. A. Interactions between externally forced climate signals from sunspot peaks and the internally generated Pacific Decadal and North Atlantic Oscillations. Geophys. Res. Lett. 41, 161–166 (2014).
Marsh, D. R. et al. Climate change from 1850 to 2005 simulated in CESM1 (WACCM). J. Clim. 26, 7372–7391 (2013).
Wang, Y.-M., Lean, J. & Sheeley, N. Modeling the Sun’s magnetic field and irradiance since 1713. Astrophys. J. 625, 522–538 (2005).
Ermolli, I. et al. Recent variability of the solar spectral irradiance and its impact on climate modelling. Atmos. Chem. Phys. 13, 3945–3977 (2013).
Crooks, S. & Gray, L. Characterization of the 11-year solar signal using a multiple regression analysis of the ERA-40 dataset. J. Clim. 18, 996–1015 (2005).
Frame, T. & Gray, L. J. The 11-year solar cycle in ERA-40 data: an update to 2008. J. Clim. 23, 2213–2222 (2010).
Chiodo, G., Marsh, D., Garcia-Herrera, R., Calvo, N. & Garca, J. On the detection of the solar signal in the tropical stratosphere. Atmos. Chem. Phys. 14, 5251–5269 (2014).
Mitchell, D. et al. Signatures of naturally induced variability in the atmosphere using multiple reanalysis datasets. Q. J. R. Meteorol. Soc. 141, 2011–2031 (2014).
Seidel, D. J. et al. Stratospheric temperature changes during the satellite era. J. Geophys. Res. 121, 664–681 (2016).
Randel, W. J., Smith, A. K., Wu, F., Zou, C. Z. & Qian, H. Stratospheric temperature trends over 1979-2015 derived from combined SSU, MLS, and SABER satellite observations. J. Clim. 29, 4843–4859 (2016).
Maycock, A., Matthes, K., Tegtmeier, S., Thiéblemont, R. & Hood, L. The representation of solar cycle signals in stratospheric ozone—part 1: a comparison of recently updated satellite observations. Atmos. Chem Phys. 16, 10021–10043 (2016).
Kay, J. et al. The Community Earth System Model (CESM) large ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteorol. Soc 96, 1333–1349 (2015).
von Salzen, K. et al. The Canadian fourth generation atmospheric global climate model (CanAM4). Part I: representation of physical processes. Atmos. Ocean 51, 104–125 (2013).
Hurrell, J. W., Kushnir, Y., Ottersen, G. & Visbeck, M. in The North Atlantic Oscillation: Climatic Significance and Environmental Impact (ed. Lifland, J.) 1–35 (American Geophysical Union, 2003).
Hurrell, J. W. & Van Loon, H. in Climate Change at High Elevation Sites (eds Diaz, H. F, Beniston, M & Bradley, R. S.) 69–94 (Springer, Berlin, 1997).
Wang, X., Li, J., Sun, C. & Liu, T. NAO and its relationship with the Northern Hemisphere mean surface temperature in CMIP5 simulations. J. Geophys. Res. 122, 4202–4227 (2017).
Wanner, H. et al. North Atlantic Oscillation—concepts and studies. Surv. Geophys. 22, 321–381 (2001).
Ortega, P. et al. A model-tested North Atlantic Oscillation reconstruction for the past millennium. Nature 523, 71–74 (2015).
Smith, D. M., Scaife, A. A., Eade, R. & Knight, J. R. Seasonal to decadal prediction of the winter North Atlantic Oscillation: emerging capability and future prospects. Q. J. R. Meteorol. Soc. 142, 611–617 (2016).
Allan, R. & Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 19, 5816–5842 (2006).
Compo, G. P. et al. The twentieth century reanalysis project. Q. J. R. Met. Soc. 137, 1–28 (2011).
Poli, P. et al. T he Data Assimilation System and Initial Performance Evaluation of the ECMWF Pilot Reanalysis of the 20th-Century Assimilating Surface Observations Only (ERA-20C) ERA Report Series No. 14 (ECMWF, 2013).
Smith, T. M. & Reynolds, R. W. Reconstruction of monthly mean oceanic sea level pressure based on COADS and station data (1854–1997). J. Atmos. Ocean Tech. 21, 1272–1282 (2004).
Gent, P. R. et al. The Community Climate System Model version 4. J. Clim. 24, 4973–4991 (2011).
Kinnison, D. et al. Sensitivity of chemical tracers to meteorological parameters in the MOZART-3 chemical transport model. J. Geophys. Res. 112, D20302 (2007).
Marsh, D. et al. Modeling the whole atmosphere response to solar cycle changes in radiative and geomagnetic forcing. J. Geophys. Res. 112, D23306 (2007).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Matthes, K. et al. Role of the QBO in modulating the influence of the 11 year solar cycle on the atmosphere using constant forcings. J. Geophys. Res. 115, D18110 (2010).
Mitchell, D. et al. Solar signals in CMIP-5 simulations: the stratospheric pathway. Q. J. R. Meteorol. Soc. 141, 2390–2403 (2015).
Hurrell, J. W. & Deser, C. North Atlantic climate variability: the role of the North Atlantic Oscillation. J. Marine Syst. 79, 231–244 (2010).
Tiao, G. et al. Effects of autocorrelation and temporal sampling schemes on estimates of trend and spatial correlation. J. Geophys. Res. 95, 20507–20517 (1990).
Acknowledgements
This work is supported by a grant from the US National Science Foundation (NSF) and a cooperative agreement between NASA and Columbia University. J.O. is funded by the NSF grant DGE 1644869. All model integrations were performed at the National Center for Atmospheric Research, which is sponsored by the US NSF. The authors thank M. Sigmond and N. Gillett (Canadian Centre for Climate Modelling and Analysis) for helpful comments. We acknowledge Environment and Climate Change Canada’s Canadian Centre for Climate Modelling and Analysis for executing and making available the CanESM2 large ensemble simulations, and the Canadian Sea Ice and Snow Evolution (CanSISE) Network for proposing the simulations.
Author information
Authors and Affiliations
Contributions
G.C. ran the climate model experiments and wrote the paper, J.O. performed the analysis of the observational and model data and G.C., J.O., L.M.P., J.C.F. and A.K.S. designed the research. All the authors helped in discussing ideas, interpreting results and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary discussion and figures
Rights and permissions
About this article
Cite this article
Chiodo, G., Oehrlein, J., Polvani, L.M. et al. Insignificant influence of the 11-year solar cycle on the North Atlantic Oscillation. Nature Geosci 12, 94–99 (2019). https://doi.org/10.1038/s41561-018-0293-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-018-0293-3
This article is cited by
-
Dimensionality reduction of chaos by feedbacks and periodic forcing is a source of natural climate change
Climate Dynamics (2024)
-
Role Of the Sun and the Middle atmosphere/thermosphere/ionosphere In Climate (ROSMIC): a retrospective and prospective view
Progress in Earth and Planetary Science (2021)
-
A 2,000-year Bayesian NAO reconstruction from the Iberian Peninsula
Scientific Reports (2020)
-
Solar Signals in Observation Indeed Implied Enhanced Predictability Since 1977
Pure and Applied Geophysics (2020)
-
Decadal variability of northern Asian winter monsoon shaped by the 11-year solar cycle
Climate Dynamics (2019)