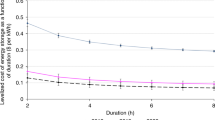
Abstract
Batteries will play critical roles in modernizing energy grids, as they will allow a greater penetration of renewable energy and perform applications that better match supply with demand. Applying storage technology is a business decision that requires potential revenues to be accurately estimated to determine the economic viability, which requires models that consider market rules and prices, along with battery and application-specific constraints. Here we use models of storage connected to the California energy grid and show how the application-governed duty cycles (power profiles) of different applications affect different battery chemistries. We reveal critical trade-offs between battery chemistries and the applicability of energy content in the battery and show that accurate revenue measurement can only be achieved if a realistic battery operation in each application is considered. The findings in this work could call for a paradigm shift in how the true economic values of energy storage devices could be assessed.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots and tables within this article, and the other findings of this study, are available from the corresponding authors upon reasonable request. Additionally, open source access to the duty cycles produced in this article is available at http://econweb.ucsd.edu/~gelliott/Charges.html.
References
Eyer, J. & Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide. A Study for the DOE Energy Storage Systems Program (Sandia National Laboratories, 2010).
Walawalkar, R., Apt, J. & Mancini, R. Economics of electric energy storage for energy arbitrage and regulation in New York. Energy Policy 35, 2558–2568 (2007).
Sioshansi, R., Denholm, P., Jenkin, T. & Weiss, J. Estimating the value of electricity storage in PJM: arbitrage and some welfare effects. Energy Econ. 31, 269–277 (2009).
Figueiredo, F. C., Flynn, P. C. & Cabral, E. A. The economics of energy storage in 14 deregulated power markets. Energy Stud. Rev. 14, 131–152 (2006).
Byrne, R. H., Concepcion, R. J. & Silva-Monroy, C. A. Estimating potential revenue from electrical energy storage in PJM. In 2016 IEEE Power and Energy Society General Meeting (PESGM) (IEEE, 2016); https://doi.org/10.1109/PESGM.2016.7741915
Fitzgerald, G., Mandel, J., Morris, J. & Touati, H. The Economics of Battery Energy Storage: How Multi-Use, Customer-Sited Batteries Deliver the Most Services and Value to Customers and the Grid (Rocky Mountain Institute, 2015).
Conover, D. et al. Protocol for Uniformly Measuring and Expressing the Performance of Energy Storage Systems (Pacific Northwest National Laboratory, Sandia National Laboratories, 2016).
Linden, D. & Reddy, T. Handbook of Batteries 4th edn (McGraw-Hill, New York, 2010).
Kjaer, S. B., Pedersen, J. K. & Blaabjerg, F. A Review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 41, 1292–1306 (2005).
Leadbetter, J. & Swan, L. G. Selection of battery technology to support grid-integrated renewable electricity. J. Power Sources 216, 376–386 (2012).
Akhil, A. A. et al. DOE/EPRI Electricity Storage Handbook in Collaboration with NRECA (Sandia National Laboratories, 2015).
Byrne, R. H., Donnelly, M. K., Loose, V. W. & Trudnowski, D. J. Methodology to Determine the Technical Performance and Value Proposition for Grid-Scale Energy Storage Systems (Sandia National Laboratories, 2012).
Xu, B., Dvorkin, Y., Kirschen, D. S., Silva-Monroy, C. A. & Watson, J.-P. A Comparison of policies on the participation of storage in U.S. frequency regulation markets. In 2016 IEEE Power and Energy Society General Meeting (PESGM) (IEEE, 2016); https://doi.org/10.1109/PESGM.2016.7741531
California Independent System Operator Corporation Flexible Ramping Product: Revised Draft Final Proposal (CAISO, 2015).
Dunn, B., Kamath, H. & Tarascon, J.-M. Electrical energy storage for the grid: a battery of choices. Science 334, 928–935 (2011).
Yang, Z. et al. Electrochemical energy storage for green grid. Chem. Rev. 111, 3577–3613 (2011).
Akhil, A., Zaininger, H., Hurtwitch, J. & Badin, J. Battery Energy Storage: A Preliminary Assessment of National Benefits (The Gateway Benefits Study) (Sandia National Laboratories, 1993).
Natron Energy announces technology evaluation agreement with EDF for grid storage applications. BusinessWire (10 July 2018).
Ragone, D. V. Review of Battery Systems for Electrically Powered Vehicles. SAE Technical Paper 680453 (SAE, 1968); https://doi.org/10.4271/680453
Joseph, A. & Shahidehpour, M. Battery storage systems in electric power systems. In 2006 IEEE Power Engineering Society General Meeting (IEEE, 2006); https://doi.org/10.1109/PES.2006.1709235
Byrne, R. H. & Silva-Monroy, A. Estimating the Maximum Potential Revenue for Grid Connected Electricity Storage: Arbitrage and Regulation (Sandia National Laboratories, 2012).
Nguyen, T. A., Byrne, R. H., Concepcion, R. J. & Gyuk, I. Maximizing revenue from electrical energy storage in MISO energy frequency regulation markets. In 2017 IEEE Power & Energy Society General Meeting (IEEE, 2017); https://doi.org/10.1109/PESGM.2017.8274348
Luo, X., Wang, J., Dooner, M. & Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 137, 511–536 (2015).
Divya, K. C. & Østergaard, J. Battery energy storage technology for power systems—an overview. Electr. Power Syst. Res. 79, 511–520 (2009).
California ISO (OASIS, accessed 23 May 2017); http://oasis.caiso.com/
Donadee, J. & Wang, J. AGC signal modeling for energy storage operations. IEEE Trans. Power Syst. 29, 2567–2568 (2014).
Specification Approval Sheet—LiFePO 4 Rechargeable Battery (Tenergy, 2014); http://www.all-battery.com/datasheet/30067_datasheet.pdf
Specification Approval Sheet—Lithium-Ion Rechargeable Battery (Tenergy, 2010); http://www.tenergy.com/30001_datasheet.pdf
Specification Approval Sheet—Nickel Cadmium Cylindrical Cell (Tenergy, 2012); http://www.tenergy.com/20203_datasheet.pdf
Cyclon Batteries (EnerSys, 2008); http://www.enersys.com/Cyclon_Batteries.aspx?langType=1033
Acknowledgements
This work was supported by the Advanced Research Projects Agency–Energy (ARPA-E), the US Department of Energy under award no. DE-AR000520 as part of the Cycling Hardware to Analyze and Ready Grid-Scale Electricity Storage (CHARGES) program. The authors express their gratitude to B. Torre and A. Tong for their time and valuable discussions, especially with regards to the applicability of this study to larger-scale ESSs. The authors also thank T. Wynn, C. Rustomji and P. Parikh for their help in editing the manuscript.
Author information
Authors and Affiliations
Contributions
D.M.D., M.G.V., G.E. and Y.S.M. designed the study. O.M., Y.R.C. and G.E. developed the forecasting techniques and algorithms for the revenue calculations. All authors contributed to developing the duty cycles for the applications. D.M.D., M.G.V. and Y.S.M. developed the cell-level testing protocols. D.M.D., M.G.V. and R.R. performed the cell-level testing and D.M.D., M.G.V. and Y.S.M performed the subsequent data analysis. D.M.D., G.E. and Y.S.M. led the writing of the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–17, Supplementary Note 1
Rights and permissions
About this article
Cite this article
Davies, D.M., Verde, M.G., Mnyshenko, O. et al. Combined economic and technological evaluation of battery energy storage for grid applications. Nat Energy 4, 42–50 (2019). https://doi.org/10.1038/s41560-018-0290-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41560-018-0290-1
This article is cited by
-
A cross-scale framework for evaluating flexibility values of battery and fuel cell electric vehicles
Nature Communications (2024)
-
Mn-based cathode materials for rechargeable batteries
Science China Chemistry (2024)
-
Fabrication of highly effective electrodes for iron chromium redox flow battery
Nano Research (2024)
-
Keystones of green smart city—framework, e-waste, and their impact on the environment—a review
Ionics (2024)
-
Nonintrusive thermal-wave sensor for operando quantification of degradation in commercial batteries
Nature Communications (2023)