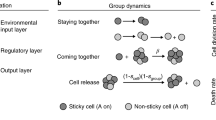
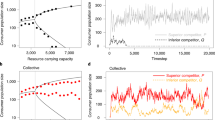
Abstract
Evolutionary transitions in individuality are central to the emergence of biological complexity. Recent experiments provide glimpses of processes underpinning the transition from single cells to multicellular life and draw attention to the critical role of ecology. Here, we emphasize this ecological dimension and argue that its current absence from theoretical frameworks hampers development of general explanatory solutions. Using mechanistic mathematical models, we show how a minimal ecological structure comprising patchily distributed resources and between-patch dispersal can scaffold Darwinian-like properties on collectives of cells. This scaffolding causes cells to participate directly in the process of evolution by natural selection as if they were members of multicellular collectives, with collectives participating in a death–birth process arising from the interplay between the timing of dispersal events and the rate of resource use by cells. When this timescale is sufficiently long and new collectives are founded by single cells, collectives experience conditions that favour evolution of a reproductive division of labour. Together our simple model makes explicit key events in the major evolutionary transition to multicellularity. It also makes predictions concerning the life history of certain pathogens and serves as an ecological recipe for experimental realization of evolutionary transitions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
All data are available within the manuscript.
Code availability
Simulation codes for the models presented in this paper are available at the GitHub repository https://github.com/andxblack/eco-scaff-paper-code under an MIT licence.
References
Buss, L. W. The Evolution of Individuality (Princeton Univ. Press, 1987).
Maynard Smith, J. & Szathmáry, E. The Major Transitions in Evolution (Freeman, 1995).
Okasha, S. Evolution and the Levels of Selection (Oxford Univ. Press, 2006).
Michod, R. E. Darwinian Dynamics: Evolutionary Transitions in Fitness and Individuality (Princeton Univ. Press, 1999).
Godfrey-Smith, P. Darwinian Populations and Natural Selection (Oxford Univ. Press, 2009).
Hull, D. L. Individuality and selection. Annu. Rev. Ecol. Syst. 11, 311–332 (1980).
Rainey, P. B. & Kerr, B. Cheats as first propagules: a new hypothesis for the evolution of individuality during the transition from single cells to multicellularity. Bioessays 32, 872–880 (2010).
Libby, E. & Rainey, P. B. A conceptual framework for the evolutionary origins of multicellularity. Phys. Biol. 10, 035001 (2013).
De Monte, S. & Rainey, P. B. Nascent multicellular life and the emergence of individuality. J. Biosci. 39, 237–248 (2014).
Lewontin, R. C. The units of selection. Annu. Rev. Ecol. Syst. 1, 1–18 (1970).
Griesemer, J. The units of evolutionary transition. Selection 1, 67–80 (2000).
Bourrat, P. From survivors to replicators: evolution by natural selection revisited. Biol. Phil. 29, 517–538 (2014).
Rainey, P. B. & De Monte, S. Resolving conflicts during the evolutionary transition to multicellular life. Annu. Rev. Ecol. Evol. Syst. 45, 599–620 (2014).
Okasha, S. The strategy of endogenization in evolutionary biology. Synthese https://doi.org/10.1007/s11229-018-1832-6 (2018).
Hanschen, E. R. et al. The Gonium pectorale genome demonstrates co-option of cell cycle regulation during the evolution of multicellularity. Nat. Commun. 7, 11370 (2016).
Ratcliff, W. C., Denison, R. F., Borrello, M. & Travisano, M. Experimental evolution of multicellularity. Proc. Natl Acad. Sci. USA 109, 1595–1600 (2012).
Wade, M. J. Adaptation in Metapopulations: How Interactions Change Evolution (Univ. Chicago Press, 2016).
Caporael, L. R., Griesemer, J. R. & Wimsatt, W. C. (eds) Developing Scaffolds in Evolution, Culture, and Cognition (Vienna Series in Theoretical Biology, MIT Press, 2014).
Hammerschmidt, K., Rose, C., Kerr, B. & Rainey, P. B. Life cycles, fitness decoupling and the evolution of multicellularity. Nature 515, 75–79 (2014).
Rose, C. J., Hammerschmidt, K., Pichugin, Y. & Rainey, P. B. Meta-population structure and the evolutionary transition to multicellularity. Preprint at bioRxiv https://doi.org/10.1101/407163 (2019).
Rainey, P. B., Remigi, P., Farr, A. D. & Lind, P. A. Darwin was right: where now for experimental evolution? Curr. Opin. Genet. Dev. 47, 102–109 (2017).
Van Valen, L. Energy and evolution. Evol.Theory 1, 179–229 (1976).
Wright, S. Evolution in Mendelian populations. Genetics 16, 97–159 (1931).
Wright, S. Tempo and mode in evolution: a critical review. Ecology 26, 415–419 (1945).
Wright, S. Evolution and the Genetics of Populations: Experimental Results and Evolutionary Deductions Vol. 3 (Univ. Chicago Press, 1977).
Maynard Smith, J. Group selection and kin selection. Nature 201, 1145–1146 (1964).
Wilson, D. S. A theory of group selection. Proc. Natl Acad Sci. USA 72, 143–146 (1975).
Goodnight, C. J. & Stevens, L. Experimental studies of group selection: what do they tell us about group selection in nature? Am. Nat. 150, S59–S79 (1997).
Traulsen, A. & Nowak, M. A. Evolution of cooperation by multilevel selection. Proc. Natl Acad. Sci. USA 103, 10952–10955 (2006).
Simon, B., Fletcher, J. A. & Doebeli, M. Towards a general theory of group selection. Evolution 67, 1561–1572 (2012).
Black, A. J. & McKane, A. J. Stochastic formulation of ecological models and their applications. Trends Ecol. Evol. 27, 337–345 (2012).
Heisler, I. L. & Damuth, J. A method for analyzing selection in hierarchically structured populations. Am. Nat. 130, 582–602 (1987).
Michod, R. E. & Roze, D. Transitions in individuality. Proc. R. Soc. B 264, 853–857 (1997).
Michod, R. E. & Nedelcu, A. M. On the reorganization of fitness during evolutionary transitions in individuality. Integr. Comp. Biol. 43, 64–73 (2003).
Clarke, E. The problem of biological individuality. Biol. Theory 5, 312–325 (2010).
Bourrat, P. Levels of selection are artefacts of different temporal fitness measures. Ratio 28, 40–50 (2015).
Bourrat, P. Levels, time and fitness in evolutionary transitions in individuality. Philos. Theor. Biol. 7, e601 (2015).
Michod, R. E. & Roze, D. in Mathematical and Computational Biology: Computational Morphogenesis, Hierarchical Complexity, and Digital Evolution (ed. Nehaniv, C.L.) 47–92 (American Mathematical Society, 1999).
Birch, J. Kin selection, group selection, and the varieties of population structure. Br. J. Philos. Sci. https://doi.org/10.1093/bjps/axx028 (2018).
Libby, E. & Ratcliff, W. C. Ratcheting the evolution of multicellularity. Science 346, 426–427 (2014).
Gallie, J. et al. Bistability in a metabolic network underpins the de novo evolution of colony switching in Pseudomonas fluorescens. PLoS Biol. 13, e1002109 (2015).
Gallie, J. et al. Repeated phenotypic evolution by different genetic routes in Pseudomonas fluorescens SBW25. Mol. Biol. Evol. 36, 1071–1085 (2019).
Remigi, P. et al. Ribosome provisioning activates a bistable switch coupled to fast exit from stationary phase. Mol. Biol. Evol. 36, 1056–1070 (2019).
Calcott, B. & Sterelny, K. (eds) The Major Transitions in Evolution Revisited (Vienna Series in Theoretical Biology, MIT Press, 2011).
Godfrey-Smith, P. & Kerr, B. Gestalt-switching and the evolutionary transitions. Br. J. Philos. Sci. 64, 205–222 (2013).
Clarke, E. Origins of evolutionary transitions. J. Biosci. 39, 1–14 (2014).
Shelton, D. E. & Michod, R. E. Group selection and group adaptation during a major evolutionary transition: insights from the evolution of multicellularity in the volvocine algae. Biol. Theory 9, 452–469 (2014).
Clarke, E. A levels-of-selection approach to evolutionary individuality. Biol. Philos. 31, 893–911 (2016).
Bourrat, P. Evolutionary transitions in individuality: a formal analysis. Synthese https://doi.org/10.1007/s11229-019-02307-5 (2019).
Queller, D. C. & Strassmann, J. E. Beyond society: the evolution of organismality. Phil. Trans. R. Soc. Lond. B 364, 3143–3155 (2009).
Bourke, A. F. Principles of Social Evolution (Oxford Univ. Press, 2011).
West, S. A., Fisher, R. M., Gardner, A. & Kiers, E. T. Major evolutionary transitions in individuality. Proc. Natl Acad. Sci. USA 112, 10112–10119 (2015).
Boraas, M. E., Seale, D. B. & Boxhorn, J. E. Phagotrophy by a flagellate selects for colonial prey: a possible origin of multicellularity. Evol. Ecol. 12, 153–164 (1998).
van Gestel, J. & Tarnita, C. E. On the origin of biological construction, with a focus on multicellularity. Proc. Natl Acad. Sci. USA 114, 11018–11026 (2017).
Herron, M. D. et al. De novo origins of multicellularity in response to predation. Sci. Rep. 9, 2328 (2019).
Rainey, P. B. Unity from conflict. Nature 446, 616 (2007).
Bourrat, P. Evolutionary transitions in heritability and individuality. Theory Biosci. 138, 305–323 (2019).
Maliet, O., Shelton, D. E. & Michod, R. E. A model for the origin of group reproduction during the evolutionary transition to multicellularity. Biol. Lett. 11, 20150157 (2015).
Griesemer, J. in Towards a Theory of Development (eds Minelli, A. & Pradeu, T.) 183–202 (Oxford Univ. Press, 2014).
Doebeli, M., Ispolatov, Y. & Simon, B. Towards a mechanistic foundation of evolutionary theory. eLife 6, e23804 (2017).
Muller, G. B. & Wagner, G. P. Novelty in evolution—restructuring the concept. Annu. Rev. Ecol. Syst. 22, 229–256 (1991).
Pfeiffer, T., Schuster, S. & Bonhoeffer, S. Cooperation and competition in the evolution of ATP-producing pathways. Science 292, 504–507 (2001).
Pfeiffer, T. & Bonhoeffer, S. An evolutionary scenario for the transition to undifferentiated multicellularity. Proc. Natl Acad. Sci. USA 100, 1095–1098 (2003).
Ewald, P. W. Evolution of Infectious Disease (Oxford Univ. Press, 1994).
Levin, B. R. & Bull, J. J. Short-sighted evolution and the virulence of pathogenic microorganisms. Trends Microbiol. 2, 76–81 (1994).
Frank, S. A. Models of parasite virulence. Q. Rev. Biol. 71, 37–78 (1996).
Frank, S. A. Natural selection. III. Selection versus transmission and the levels of selection. J. Evol. Biol. 25, 227–243 (2012).
Lythgoe, K. A., Pellis, L. & Fraser, C. Is HIV short-sighted? insights from a multistrain nested model. Evolution 67, 2769–2782 (2013).
Cressler, C. E., McLeod, D. V., Rozins, C., van den Hoogen, J. & Day, T. The adaptive evolution of virulence: a review of theoretical predictions and empirical tests. Parasitology 143, 915–930 (2016).
Frank, S. A. Demography and the tragedy of the commons. J. Evol. Biol. 23, 32–39 (2010).
Anderson, R. M. & May, R. M. Infectious Diseases of Humans (Oxford Univ. Press, 1991).
Keeling, M. J. & Rohani, P. Modeling Infectious Diseases in Humans and Animals (Princeton Univ. Press, 2007).
Lythgoe, K. A., Gardner, A., Pybus, O. G. & Grove, J. Short-sighted virus evolution and a germline hypothesis for chronic viral infections. Trends Microbiol. 25, 336–348 (2017).
Staps, M., van Gestel, J. & Tarnita, C. E. Emergence of diverse life cycles and life histories at the origin of multicellularity. Nat. Ecol. Evol. 3, 1197 (2019).
Wilson, D. S. & Sober, E. Reviving the superorganism. J. Theor. Biol. 136, 337–356 (1989).
Hamilton, W. D. The genetical evolution of social behavior, I & II. J. Theor. Biol. 7, 1–52 (1964).
Wilson, E. O. & Holldobler, B. Eusociality: origin and consequences. Proc. Natl Acad. Sci. USA 102, 13367–13371 (2005).
Gardner, A. & Grafen, A. Capturing the superorganism: a formal theory of group adaptation. J. Evol. Biol. 22, 659–671 (2009).
Martin, W. & Russell, M. J. On the origin of biochemistry at an alkaline hydrothermal vent. Phil. Trans. R. Soc. Lond. B 362, 1887–1925 (2007).
Lane, N. The Vital Question: Why is Life the Way it is? (Profile Books, 2015).
Diard, M. et al. Stabilization of cooperative virulence by the expression of an avirulent phenotype. Nature 494, 353–356 (2013).
Swenson, W., Wilson, D. S. & Elias, R. Artificial ecosystem selection. Proc. Natl Acad. Sci. USA 97, 9110–9114 (2000).
Xie, L., Yuan, A. E. & Shou, W. Y. Simulations reveal challenges to artificial community selection and possible strategies for success. PLoS Biol. 17, e3000295 (2019).
Cottinet, D. et al. Lineage tracking for probing heritable phenotypes at single-cell resolution. PLoS ONE 11, e0152395 (2016).
Doulcier, G., Lambert, A. J., De Monte, S. & Rainey, P. B. Eco-evolutionary dynamics of nested Darwinian populations and the emergence of community-level heredity. Preprint at bioRxiv https://doi.org/10.1101/827592 (2019).
Renshaw, E. Modelling Biological Populations in Space and Time (Cambridge Univ. Press, 1993).
Brauer, F. & Castillo-Chávez, C. Mathematical Models in Population Biology and Epidemiology (Springer, 2001).
Davis, M. H. A. Piecewise-deterministic Markov processes: a general class of non-diffusion stochastic models. J. R. Stat. Soc. B 46, 353–388 (1984).
Acknowledgements
We thank J. Wietz for critical review of the manuscript and valuable comment. We thank S. De Monte, G. Doulcier, M. Diard and members of our respective teams for lively discussion. A.J.B. acknowledges an Australian Research Council (ARC) DECRA fellowship (grant no. DE160100690) and support from both the ARC Centre of Excellence for Mathematical and Statistical Frontiers (CoE ACEMS) and the Australian Government NHMRC Centre for Research Excellence in Policy Relevant Infectious diseases Simulation and Mathematical Modelling (CRE PRISM2). P.B. acknowledges a Macquarie University Research Fellowship and a grant from the John Templeton Foundation (grant no. ID 60811). P.B.R. acknowledges generous financial support from MPG core funding and previously from the Marsden Fund Council from New Zealand Government funding, administered by the Royal Society of New Zealand.
Author information
Authors and Affiliations
Contributions
P.B.R. and P.B. developed the main concepts. A.J.B. contributed the mathematical models and ran simulations to clarify initial ideas. All authors wrote and revised the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Genealogy of patches under slow (A) and fast (B) dispersal regimes.
The simulations have only 10 patches and modified mutational parameters compared with those in Fig. 2 of the main text. This is to allow a clearer visualization of the process, which otherwise requires many more generations for change to be apparent. Video versions of these are also included in the supplementary material. As in Figs. 4 and 5 of the main text, the cell numbers in each patch are proportional to the area of the circles and the growth rates are indicated by the colours, as shown by the colour bar in Fig. 4 of the main text. The mutational parameters are larger for these simulations (µ=0.05, p = 0.05) so evolution occurs on a quicker timescale as compared with the results shown in Fig. 3 of the main text.
Extended Data Fig. 2 Simulations of the model with sterile types over 2000 generations show convergence to equilibrium.
The comparative slowness of this convergence, as well as the large fluctuations in the mean value of q for single realizations, can be attributed to the flatness of the fitness landscape about the equilibrium as shown in the Supplementary Information.
Extended Data Fig. 3 Change in the position of the equilibrium as a function of the dispersal assistance provided by S cells assistance ρ for slow dispersal.
Fitness landscapes showing the effect of changes in the assistance, ρ, given to dispersing G cells by non-dispersing S cells on the equilibrium (*) relationship between cell growth rate, β, and the rate of production of S cells, q, under the slow (T = 30) dispersal regime.
Supplementary information
Supplementary Information
Supplementary Figs. 1–7, text and references.
Supplementary Video 1
Single realization of the model under the slow dispersal regime as shown in Fig 4A.
Supplementary Video 2
Single realization of the model under the fast dispersal regime as shown in Fig 4B.
Supplementary Video 3
Evolutionary fate of 10 lineages under the slow dispersal regime as shown in Extended Data 1A.
Supplementary Video 4
Evolutionary fate of 10 lineages under the fast dispersal regime as shown in Extended Data 1B.
Rights and permissions
About this article
Cite this article
Black, A.J., Bourrat, P. & Rainey, P.B. Ecological scaffolding and the evolution of individuality . Nat Ecol Evol 4, 426–436 (2020). https://doi.org/10.1038/s41559-019-1086-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41559-019-1086-9
This article is cited by
-
Context Matters: A Response to Autzen and Okasha’s Reply to Takacs and Bourrat
Biological Theory (2024)
-
Adding causality to the information-theoretic perspective on individuality
European Journal for Philosophy of Science (2024)
-
The role of the ecological scaffold in the origin and maintenance of whole-group trait altruism in microbial populations
BMC Ecology and Evolution (2023)
-
Moving Past Conventionalism About Multilevel Selection
Erkenntnis (2023)
-
Multilevel selection 1, multilevel selection 2, and the Price equation: a reappraisal
Synthese (2023)