Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Short-range interactions govern the dynamics and functions of microbial communities

Nature Ecology & Evolution volume 4, pages 366–375 (2020)Cite this article

Subjects

An Author Correction to this article was published on 18 March 2021

A Publisher Correction to this article was published on 16 March 2020

This article has been updated

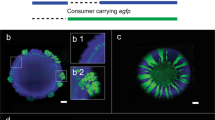
Abstract

Communities of interacting microorganisms play important roles across all habitats on Earth. These communities typically consist of a large number of species that perform different metabolic processes. The functions of microbial communities ultimately emerge from interactions between these different microorganisms. To understand the dynamics and functions of microbial communities, we thus need to know the nature and strength of these interactions. Here, we quantified the interaction strength between individual cells in microbial communities. We worked with synthetic communities of Escherichia coli bacteria that exchange metabolites to grow. We combined single-cell growth rate measurements with mathematical modelling to quantify metabolic interactions between individual cells and to map the spatial interaction network in these communities. We found that cells only interact with other cells in their immediate neighbourhood. This short interaction range limits the coupling between different species and reduces their ability to perform metabolic processes collectively. Our experiments and models demonstrate that the spatial scale of biotic interaction plays a fundamental role in shaping the ecological dynamics of communities and the functioning of ecosystems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Interacting locally lowers reproductive success.
Fig. 2: Auxotrophic cells that exchange cellular building blocks interact in a small range.
Fig. 3: Mathematical model reveals the mechanism of local interactions.
Fig. 4: Interaction range is small when uptake rates are high.
Fig. 5: The small interaction range between cells reduces the productivity of the consortium.

Similar content being viewed by others

Data availability

The source data for all figures are available in the Supplementary Figure Source Data file. A data file containing the full properties of all analysed cells is available in the ETH Research Collection: https://doi.org/10.3929/ethz-b-000367403. The raw image data are available on request from the corresponding author.

Code availability

The code for the individual-based model is available on the Zenodo repository: https://doi.org/10.5281/zenodo.3466038. Additional Matlab scripts for statistical analysis are available on request.

Change history

References

  1. Proulx, S. R., Promislow, D. E. L. & Phillips, P. C. Network thinking in ecology and evolution. Trends Ecol. Evol. 20, 345–353 (2005).

    PubMed  Google Scholar 

  2. Levin, S. A. Ecosystems and the biosphere as complex adaptive systems. Ecosystems 1, 431–436 (1998).

    Google Scholar 

  3. Pickett, S. T. A. & Cadenasso, M. L. Landscape ecology: spatial heterogeneity in ecological systems. Science 269, 331–334 (1995).

    CAS  PubMed  Google Scholar 

  4. Agrawal, A. A. et al. Filling key gaps in population and community ecology. Front. Ecol. Environ. 5, 145–152 (2007).

    Google Scholar 

  5. Falkowski, P. G., Fenchel, T. & Delong, E. F. The microbial engines that drive Earth’s biogeochemical cycles. Science 320, 1034–1039 (2008).

    CAS  PubMed  Google Scholar 

  6. Lynch, S. V. & Pedersen, O. The human intestinal microbiome in health and disease. New Engl. J. Med. 375, 2369–2379 (2016).

    CAS  PubMed  Google Scholar 

  7. Gore, J. Simple organizing principles in microbial communities. Curr. Opin. Microbiol. 45, 195–202 (2018).

    PubMed  Google Scholar 

  8. Nadell, C. D., Drescher, K. & Foster, K. R. Spatial structure, cooperation and competition in biofilms. Nat. Rev. Microbiol. 14, 589–600 (2016).

    CAS  PubMed  Google Scholar 

  9. Flemming, H.-C. et al. Biofilms: an emergent form of bacterial life. Nat. Rev. Microbiol. 14, 563–575 (2016).

    CAS  PubMed  Google Scholar 

  10. Tan, J., Zuniga, C. & Zengler, K. Unraveling interactions in microbial communities—from co-cultures to microbiomes. J. Microbiol. 53, 295–305 (2015).

    PubMed  Google Scholar 

  11. D’Souza, G. et al. Less is more: selective advantages can explain the prevalent loss of biosynthetic genes in bacteria. Evolution 68, 2559–2570 (2014).

    PubMed  Google Scholar 

  12. Mee, M. T., Collins, J. J., Church, G. M. & Wang, H. H. Syntrophic exchange in synthetic microbial communities. Proc. Natl Acad. Sci. USA 111, E2149–E2156 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  13. Schink, B. Synergistic interactions in the microbial world. A. Van Leeuw. 81, 257–261 (2002).

    CAS  Google Scholar 

  14. Christensen, B. B., Haagensen, J. A. J. J., Heydorn, A. & Molin, S. Metabolic commensalism and competition in a two-species microbial consortium. Appl. Environ. Microbiol. 68, 2495–2502 (2002).

    CAS  PubMed  PubMed Central  Google Scholar 

  15. Dal Co, A., Ackermann, M. & van Vliet, S. Metabolic activity affects the response of single cells to a nutrient switch in structured populations. J. R. Soc. Interface 16, 20190182 (2019).

    PubMed  PubMed Central  Google Scholar 

  16. Rutherford, S. T. & Bassler, B. L. Bacterial quorum sensing: its role in virulence and possibilities for its control. Cold Spring Harb. Perspect. Med. 2, a012427 (2012).

    PubMed  PubMed Central  Google Scholar 

  17. van Vliet, S. et al. Spatially correlated gene expression in bacterial groups: the role of lineage history, spatial gradients, and cell–cell interactions. Cell Syst. 6, 496–507 (2018).

    PubMed  PubMed Central  Google Scholar 

  18. Flemming, H.-C. & Wuertz, S. Bacteria and archaea on Earth and their abundance in biofilms. Nat. Rev. Microbiol. 17, 247–260 (2019).

    CAS  PubMed  Google Scholar 

  19. Muller, M. J. I., Neugeboren, B. I., Nelson, D. R. & Murray, A. W. Genetic drift opposes mutualism during spatial population expansion. Proc. Natl Acad. Sci. USA 111, 1037–1042 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  20. Darch, S. E. et al. Spatial determinants of quorum signaling in a Pseudomonas aeruginosa infection model. Proc. Natl Acad. Sci. USA 115, 201719317 (2018).

    Google Scholar 

  21. He, X. et al. Microbial interactions in the anaerobic oxidation of methane: model simulations constrained by process rates and activity patterns. Environ. Microbiol. 21, 631–647 (2019).

    CAS  PubMed  Google Scholar 

  22. Drescher, K., Nadell, C. D., Stone, H. A., Wingreen, N. S. & Bassler, B. L. Solutions to the public goods dilemma in bacterial biofilms. Curr. Biol. 24, 50–55 (2014).

    CAS  PubMed  Google Scholar 

  23. McGlynn, S. E., Chadwick, G. L., Kempes, C. P. & Orphan, V. J. Single cell activity reveals direct electron transfer in methanotrophic consortia. Nature 526, 531–535 (2015).

    CAS  PubMed  Google Scholar 

  24. Momeni, B., Waite, A. J. & Shou, W. Spatial self-organization favors heterotypic cooperation over cheating. eLife 2, e00960 (2013).

    PubMed  PubMed Central  Google Scholar 

  25. Stump, S. M., Johnson, E. C., Sun, Z. & Klausmeier, C. A. How spatial structure and neighbor uncertainty promote mutualists and weaken black queen effects. J. Theor. Biol. 446, 33–60 (2018).

    PubMed  Google Scholar 

  26. Stump, S. M., Johnson, E. C. & Klausmeier, C. A. Local interactions and self-organized spatial patterns stabilize microbial cross-feeding against cheaters. J. R. Soc. Interface 15, 20170822 (2018).

    PubMed  PubMed Central  Google Scholar 

  27. Nowak, M. A., Tarnita, C. E. & Antal, T. Evolutionary dynamics in structured populations. Phil. Trans. R. Soc. B 365, 19–30 (2010).

    PubMed  PubMed Central  Google Scholar 

  28. Egland, P. G., Palmer, R. J. & Kolenbrander, P. E. Interspecies communication in Streptococcus gordonii–Veillonella atypica biofilms: signaling in flow conditions requires juxtaposition. Proc. Natl Acad. Sci. USA 101, 16917–16922 (2004).

    CAS  PubMed  PubMed Central  Google Scholar 

  29. Morris, J. J. Black queen evolution: the role of leakiness in structuring microbial communities. Trends Genet. 31, 475–482 (2015).

    CAS  PubMed  Google Scholar 

  30. Oliveira, N. M., Niehus, R. & Foster, K. R. Evolutionary limits to cooperation in microbial communities. Proc. Natl Acad. Sci. USA 111, 17941–17946 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  31. D’Souza, G. et al. Ecology and evolution of metabolic cross-feeding interactions in bacteria. Nat. Prod. Rep. 35, 455–488 (2018).

    PubMed  Google Scholar 

  32. Marchal, M. et al. A passive mutualistic interaction promotes the evolution of spatial structure within microbial populations. BMC Evol. Biol. 17, 106 (2017).

    PubMed  PubMed Central  Google Scholar 

  33. Lebenhaft, J. R. & Kapral, R. Diffusion-controlled processes among partially absorbing stationary sinks. J. Stat. Phys. 20, 25–56 (1979).

    Google Scholar 

  34. Dobay, A., Bagheri, H. C., Messina, A., Kümmerli, R. & Rankin, D. J. Interaction effects of cell diffusion, cell density and public goods properties on the evolution of cooperation in digital microbes. J. Evol. Biol. 27, 1869–1877 (2014).

    CAS  PubMed  Google Scholar 

  35. Lindsay, R. J., Pawlowska, B. J. & Gudelj, I. When increasing population density can promote the evolution of metabolic cooperation. ISME J. 12, 849–859 (2018).

    PubMed  PubMed Central  Google Scholar 

  36. Ross-Gillespie, A. & Kümmerli, R. Collective decision-making in microbes. Front. Microbiol. 5, 54 (2014).

    PubMed  PubMed Central  Google Scholar 

  37. Stacy, A. et al. Bacterial fight-and-flight responses enhance virulence in a polymicrobial infection. Proc. Natl Acad. Sci. USA 111, 7819–7824 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  38. Hol, F. J. H. et al. Spatial structure facilitates cooperation in a social dilemma: empirical evidence from a bacterial community. PLoS ONE 8, e77042 (2013).

    CAS  PubMed  PubMed Central  Google Scholar 

  39. Mitri, S., Xavier, J. B. & Foster, K. R. Social evolution in multispecies bio films. Proc. Natl Acad. Sci. USA 108, 10839–10846 (2011).

    CAS  PubMed  PubMed Central  Google Scholar 

  40. Davies, D. G. & Geesey, G. G. Regulation of the alginate biosynthesis gene algC in Pseudomonas aeruginosa during biofilm development in continuous culture. Appl. Environ. Microbiol. 61, 860–867 (1995).

    CAS  PubMed  PubMed Central  Google Scholar 

  41. Saha, M. et al. Microbial siderophores and their potential applications: a review. Environ. Sci. Pollut. Res. 23, 3984–3999 (2016).

    CAS  Google Scholar 

  42. Leventhal, G. E. & Ackermann, M. & Schiessl, K. T. Why microbes secrete molecules to modify their environment: the case of iron-chelating siderophores. J. R. Soc. Interface 16, 20180674 (2019).

    CAS  PubMed  PubMed Central  Google Scholar 

  43. DeMalach, N., Zaady, E., Weiner, J. & Kadmon, R. Size asymmetry of resource competition and the structure of plant communities. J. Ecol. 104, 899–910 (2016).

    Google Scholar 

  44. Soliveres, S., Smit, C. & Maestre, F. T. Moving forward on facilitation research: response to changing environments and effects on the diversity, functioning and evolution of plant communities. Biol. Rev. 90, 297–313 (2015).

    PubMed  Google Scholar 

  45. Schmitz, O. J., Miller, J. R. B., Trainor, A. M. & Abrahms, B. Toward a community ecology of landscapes: predicting multiple predator–prey interactions across geographic space. Ecology 98, 2281–2292 (2017).

    PubMed  Google Scholar 

  46. Baba, T. et al. Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol. Syst. Biol. 2, 2006.0008 (2006).

    PubMed  PubMed Central  Google Scholar 

  47. Tomasek, K., Bergmiller, T. & Guet, C. C. Lack of cations in flow cytometry buffers affect fluorescence signals by reducing membrane stability and viability of Escherichia coli strains. J. Biotechnol. 268, 40–52 (2018).

    CAS  PubMed  Google Scholar 

  48. Datsenko, K. A. & Wanner, B. L. One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proc. Natl Acad. Sci. USA 97, 6640–6645 (2000).

    CAS  PubMed  PubMed Central  Google Scholar 

  49. Olympus CellSens software v.1.16 (Olympus, 2019).

  50. Kiviet, D. J. Vanellus Software version Feb 11 (2019); https://github.com/daankiviet/vanellus

  51. Farneback, G. Two-frame motion estimation based on polynomial expansion. Image Anal. Proc. 2749, 363–370 (2003).

    Google Scholar 

Download references

Acknowledgements

We thank A. Cavagna for discussing the correlation analysis; G. D’Souza for advice on the biological assumptions of the model; G. Micali, R. Stocker and M. Doebeli for comments on the model; K. Schlegel for performing a plate reader experiment; A. von Wyl for helping correct cell tracking errors; and C. Brannon for comments on the manuscript. The research was supported by funding from the Swiss National Science Foundation (grant nos 31003A_149267 and 31003A_169978 to M.A.), by an ETH fellowship to D.J.K., by an Early Postdoc Mobility fellowship from the Swiss National Science Foundation to S.v.V. (grant no. 175123) and by ETH Zurich and Eawag.

Author information

Authors and Affiliations

  1. Department of Environmental Systems Science, ETH Zurich, Zurich, Switzerland

    Alma Dal Co, Simon van Vliet, Daniel Johannes Kiviet, Susan Schlegel & Martin Ackermann

  2. Department of Environmental Microbiology, Eawag, Duebendorf, Switzerland

    Alma Dal Co, Simon van Vliet, Daniel Johannes Kiviet, Susan Schlegel & Martin Ackermann

  3. Department of Zoology, University of British Columbia, British Columbia, Vancouver, Canada

    Simon van Vliet

Authors
  1. Alma Dal Co
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Simon van Vliet
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Daniel Johannes Kiviet
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Susan Schlegel
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Martin Ackermann
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.D.C. and M.A. conceived the research. A.D.C. performed the experiment with contributions from S.v.V. A.D.C. developed the statistical analysis and analysed the data. A.D.C. and D.J.K. developed the image analysis. S.v.V. and A.D.C. conceptualized the individual-based model, and S.v.V. implemented it. S.S. constructed the bacterial strains. D.J.K. constructed the microfluidic device. A.D.C. and M.A. wrote the manuscript with contributions from S.v.V.

Corresponding author

Correspondence to Alma Dal Co.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Growth does not depend on the identity of neighbours when amino acids are fed.

When media is supplemented with proline and tryptophan, the growth of the auxotrophic cells does not depend on the presence of the partner near by. The correlation between growth rate of cells and fraction of the partner is low for all neighbourhood sizes analysed. Panel a shows results for consortium 1 (ΔtrpC-GFP and ΔproC-RFP, 445 and 591 cells analysed respectively), panel b for consortium 2 (ΔtrpC-RFP and ΔproC-GFP, 1,905 and 2,067 cells analysed respectively).

Extended Data Fig. 2 Growth of cells does not depend on their distance from the chamber’s opening.

The growth of both auxotrophic cells correlates weakly with the distance from the chamber’s opening into the feeding channel (“depth” in the figure): ρ=0.07, p<10−4, n= 4,567 for ΔtrpC and ρ=0.05, p<10−4, n= 5,905 for ΔproC, Spearman.

Extended Data Fig. 3 Robustness of interaction range estimate to spatial arrangement of types.

Examples of artificial arrangements with controlled patch size; dataset of 100 different arrangements per patch size were generated and analysed. The shape of the correlation curve changes for both proline (b) and tryptophan (c) auxotrophs, but the interaction range changes only minimally (d) for a range of patch sizes that can be observed in the data.

Extended Data Fig. 4 Size of a patch does not correlate with its growth rate.

The two different cell types in our system form patches because two daughter cells tend to remain close in space after division. Contrary to intuition, larger patches do not imply higher growth rate of the patch (analysis done on the tryptophan auxotrophs), because cells in the interior of a large patch tend to grow slower or not at all, as they cannot retrieve the amino acids they need. ρ=0.32, p=0.025, n=50, Spearman correlation.

Extended Data Fig. 5 Very low uptake rates reduce growth of cells if amino acids can diffuse out of the system.

Using our model, we estimated how fast cells would grow if their growth range (and interaction range) would increase by lowering uptake rates of amino acids. When simulating systems open on one side, like our chambers, the auxotrophs grow slower (relative growth rate is below one) when they have a very large growth range (and interaction range), that is when they have very low uptake rates of the amino acids. Yellow indicates tryptophan auxotroph, purple indicates proline auxotroph. Relative growth rates are the average growth rates cells would have in our real spatial configurations when we vary the uptake rates of amino acids, divided by the growth rates cells have with the actual uptake rates of amino acids (uptake rates values are taken from literature, see Supplementary Table 1). Figure shows results for consortium 1 (total of 22 chambers).

Extended Data Fig. 6 Individuals interact at a small spatial range.

All three panels shows data for consortium 2 (ΔtrpC-RFP and ΔproC-GFP), and complement Fig. 2 showing data from consortium 1 (ΔtrpC-GFP and ΔproC-RFP). a, The cells’ growth rate correlates maximally with the identity of their neighbours within the interaction range. b, c, Both auxotrophic cells grow faster when surrounded by more complementary partners inside the interaction range. Tryptophan auxotrophs (b) achieve generally smaller growth rates then proline auxotrophs (c), as shown by the slopes of the linear regression (0.79 for ΔproC and 0.089 for ΔtrpC). Black dots: single cells (3,920 for ΔproC and 2,798 for ΔtrpC); open symbols: binned median values; lines: linear regression on binned values.

Extended Data Fig. 7 Growth rate in batch cultures of wild type and auxotroph strains.

Wild type cells grow at a similar rate in M9 glucose medium without amino acids (WT) and in M9 glucose medium supplemented with 50 μg/mL of proline (WT+P), 20 μg/mL of tryptophan (WT+T), or both (WT+PT). The auxotrophic mutants in consortium 1 (ΔtrpC-GFP + ΔproC-RFP) grow at the same rate as the wild type. The proline auxotroph was grown in medium supplemented with 50 μg/mL of proline and the tryptophan auxotroph in medium supplemented with 20 μg/mL of tryptophan. Markers show maximal growth rates in batch culture of individual replicates (n=12), bars show average values. Shared letters (top of panel) indicate no significant difference in growth rate (ANOVA analysis with post-hoc Tukey-Kramer pairwise comparison, F=3.29, df=7, p=4*10−3. The wild type strains (WT) are the strains expressing the red and green fluorescent proteins (TB205 expressing RFP and TB204 expressing GFP, see details about the strains construction in Methods). The growth measurements of these strains was pooled together because they had no significant growth difference (ANOVA analysis on growth rate data of wild type in all four growth media, testing for the effect of medium F=2.53, df=3, p=0.07 and color label F=0.02, df=1, p=0.88.

Extended Data Fig. 8 The interaction range varies minimally with the leakage rate.

a, b, The predicted interaction range is consistent with the experimentally measured one across a large range of possible leakage rates. The interaction range of the two auxotrophs was predicted using the model while varying the leakage rates of the amino acids. The model was solved on experimentally measured spatial arrangements. The dashed horizontal lines and shaded regions indicate the mean and 95% confidence interval of the experimentally measured interaction ranges. The dashed vertical line indicates the fitted leakage rate used in all simulations. c, The predicted relative interaction range is consistent with the experimentally measured one over a large range of possible leakage rates. The relative interaction range (interaction range of ΔP divided by that of ΔT) was predicted using the model while varying the leakage rates of the amino acids. The x axis shows the geometric mean value of the leakage rate \(r^l = \sqrt {r_{\Delta P}^l \ast r_{\Delta T}^l}\), the different colored lines show different ratios of the leakage rates of the two amino acids \(\frac{{r_{\Delta P}^l}}{{r_{\Delta T}^l}}\). The dashed horizontal line and shaded region indicate the mean and 95% confidence interval of the experimentally measured relative interaction range. The dashed vertical line indicates the fitted leakage rate used in all simulations (fitted \({\frac{{r_{\Delta P}^l}}{{r_{\Delta T}^l}}=26}\)). d, Cross-validation of model. The leakage rate was fitted to data from consortium 1 and the interaction range was calculated using the model. This prediction (based solely on data from consortium 1) was compared to the experimentally measured interaction range in consortium 2. The model can quantitatively predict the interaction range (p=0.16, n=6 for ΔT and p=0.35, n=6 for ΔP, t-test).

Extended Data Fig. 9 Analytical approximation of growth range and simulations agree.

The heat map in b shows the relative error between analytical approximation (eq. 33) for the growth range and the growth range estimated with simulations. The heat map in a shows the analytical estimate of the growth range, and shows that the relative error in b is low when the growth range is below 20. Purple circle is proline auxotroph and yellow circle is tryptophan auxotroph. Panel a shows the same data as Fig. 4c.

Extended Data Fig. 10 Effect of density of cells on diffusion of molecules.

a, Dependence of Deff and \(\frac{{D^{eff}}}{\alpha }\) on the cellular density. High cellular densities reduce the effective diffusion of molecules. In our microfluidic chambers cellular density is about 0.65 (that is fraction of the chamber’s volume occupied by cells). b, The growth range decreases with higher cellular densities. The analytically predicted growth range (eq. 33 in Supplementary Information) is shown as function of cellular density. The dashed lines indicate the predicted growth range at the experimentally measured cellular density. All other parameters are indicated in Supplementary Table 1.

Supplementary information

Supplementary Information

Supplementary discussion, data, equations, methods and references.

Reporting Summary

Supplementary Video 1

Supplementary Video 1: The three-dimensional rendering shows the microfluidic device used for all experiments. The microfluidic device consists of chambers of 60 × 60 μm and 0.76 μm in height facing a feeding channel of 22 μm in height and 100 μm in width. E. coli cells grow in monolayer communities in the chambers and are imaged using time-lapse microscopy. Thin tubing connects the inlet of the feeding channel to syringes containing fresh media, and the outlet to a waste collection. Media continuously flows in the feeding channel providing the bacteria with fresh nutrients as they grow in the chambers.

Supplementary Video 2

Supplementary Video 2: Two auxotrophic strains of E. coli grow in microfluidic chambers of 60 × 60 μm. Left: False coloured fluorescence images show proline auxotrophic cells in purple and tryptophan auxotrophic cells in yellow. Right: The same cells are coloured based on their growth rate, with lighter colours indicating higher growth rates. Growth rates are higher for auxotrophic cells close to the partner. One cell type (in purple) has higher growth rates further away from the partner.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dal Co, A., van Vliet, S., Kiviet, D.J. et al. Short-range interactions govern the dynamics and functions of microbial communities. Nat Ecol Evol 4, 366–375 (2020). https://doi.org/10.1038/s41559-019-1080-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41559-019-1080-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing Microbiology

Sign up for the Nature Briefing: Microbiology newsletter — what matters in microbiology research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: Microbiology