Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Global patterns and drivers of tree diversity integrated across a continuum of spatial grains

Nature Ecology & Evolution volume 3, pages 390–399 (2019)Cite this article

Subjects

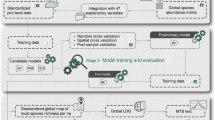
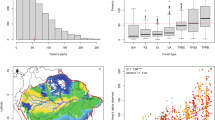
Abstract

Controversy remains over what drives patterns in the variation of biodiversity across the planet. The resolution is obscured by lack of data and mismatches in their spatial grain (scale), and by grain-dependent effects of the drivers. Here we introduce cross-scale models integrating global data on tree-species richness from 1,336 local forest surveys and 282 regional checklists, enabling the estimation of drivers and patterns of biodiversity across spatial grains. We uncover grain-dependent effects of both environment and biogeographic regions on species richness, with a striking positive effect of Southeast Asia at coarse grain that disappears at fine grains. We show that, globally, biodiversity cannot be attributed purely to environmental or regional drivers, as the regions are environmentally distinct even within a single latitudinal band. Finally, we predict global maps of biodiversity at local (plot-based) and regional grains, identifying areas of exceptional beta-diversity in China, East Africa and North America. By allowing the importance of drivers of diversity to vary with grain in a single model, our approach unifies disparate results from previous studies regarding environmental versus biogeographic predictors of biodiversity, and enables efficient integration of heterogeneous data.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

All data and R codes used for the analyses are available under CC-BY 4.0 license in a GitHub repository at https://github.com/petrkeil/global_tree_S, which is also mirrored at figshare at https://figshare.com/articles/global_tree_S/7461509. Please note that if the data on species richness are reused, the original data sources should be credited.

References

  1. Fine, P. V. A. & Ree, R. H. Evidence for a time-integrated species-area effect on the latitudinal gradient in tree diversity. Am. Nat. 168, 796–804 (2006).

    PubMed  Google Scholar 

  2. Frodin, D. G. Guide to Standard Floras of the World (Cambridge Univ. Press, Cambridge, 2001).

  3. Losos, E. & Leigh, E. G. Tropical Forest Diversity and Dynamism (Univ. of Chicago Press, Chicago, 2004).

  4. Hawkins, B. A. Ecology’s oldest pattern? Trends Ecol. Evol. 16, 470 (2001).

    Google Scholar 

  5. Storch, D., Bohdalková, E. & Okie, J. The more-individuals hypothesis revisited: the role of community abundance in species richness regulation and the productivity-diversity relationship. Ecol. Lett. 21, 920–937 (2018).

    PubMed  Google Scholar 

  6. Currie, D. J. et al. Predictions and tests of climate-based hypotheses of broad-scale variation in taxonomic richness. Ecol. Lett. 7, 1121–1134 (2004).

    Google Scholar 

  7. Ricklefs, R. E. & He, F. Region effects influence local tree species diversity. Proc. Natl Acad. Sci. USA 113, 674–679 (2016).

    CAS  PubMed  Google Scholar 

  8. Wiens, J. J. et al. Niche conservatism as an emerging principle in ecology and conservation biology. Ecol. Lett. 13, 1310–1324 (2010).

    PubMed  Google Scholar 

  9. Rabosky, D. L. & Hurlbert, A. H. Species richness at continental scales is dominated by ecological limits. Am. Nat. 185, 572–583 (2015).

    PubMed  Google Scholar 

  10. Meyer, C., Kreft, H., Guralnick, R. & Jetz, W. Global priorities for an effective information basis of biodiversity distributions. Nat. Commun. 6, 8221 (2015).

    PubMed  PubMed Central  Google Scholar 

  11. Jetz, W., McPherson, J. M. & Guralnick, R. P. Integrating biodiversity distribution knowledge: toward a global map of life. Trends Ecol. Evol. 27, 151–159 (2012).

    PubMed  Google Scholar 

  12. Phillips, O. L. & Miller, J. S. Global Patterns of Plant Piversity: Alwyn H. Gentry’s Forest Transect Data Set (Missouri Botanical Garden Press, St. Louis, 2002).

  13. Sullivan, M. et al. Diversity and carbon storage across the tropical forest biome. Sci. Rep. 7, 39102 (2017).

    CAS  PubMed  PubMed Central  Google Scholar 

  14. GlobalTreeSearch Online Database (BCGI, 2017); https://www.bgci.org/global_tree_search.php

  15. Enquist, B. J., Condit, R., Peet, R. K., Schildhauer, M. & Thiers, B. M. Cyberinfrastructure for an integrated botanical information network to investigate the ecological impacts of global climate change on plant biodiversity. PeerJ Preprints 4, e2615v2 (2016).

    Google Scholar 

  16. Levin, S. A. Multiple scales and the maintenance of biodiversity. Ecosystems 3, 498–506 (2000).

    Google Scholar 

  17. Chave, J. The problem of pattern and scale in ecology: what have we learned in 20 years? Ecol. Lett. 16, 4–16 (2013).

    PubMed  Google Scholar 

  18. Chase, J. M. Spatial scale resolves the niche versus neutral theory debate. J. Veg. Sci. 25, 319–322 (2014).

    Google Scholar 

  19. Leibold, M. A. & Chase, J. M. Metacommunity Ecology (Princeton Univ. Press, Princeton, 2017).

  20. Storch, D. The theory of the nested species–area relationship: geometric foundations of biodiversity scaling. J. Veg. Sci. 27, 880–891 (2016).

    Google Scholar 

  21. Rahbek, C. The role of spatial scale and the perception of large-scale species-richness patterns. Ecol. Lett. 8, 224 (2005).

    Google Scholar 

  22. Rahbek, C. & Graves, G. R. Detection of macro-ecological patterns in South American hummingbirds is affected by spatial scale. Proc. R. Soc. B 267, 2259–2265 (2000).

    CAS  PubMed  Google Scholar 

  23. Chase, J. M. & Knight, T. M. Scale-dependent effect sizes of ecological drivers on biodiversity: why standardised sampling is not enough. Ecol. Lett. 16, 17–26 (2013).

    PubMed  Google Scholar 

  24. Blowes, S. A., Belmaker, J. & Chase, J. M. Global reef fish richness gradients emerge from divergent and scale-dependent component changes. Proc. R. Soc. B 284, 20170947 (2017).

    PubMed  Google Scholar 

  25. Kraft, N. J. B. et al. Disentangling the drivers of β diversity along latitudinal and elevational gradients. Science 333, 1755–1758 (2011).

    CAS  PubMed  Google Scholar 

  26. Buckley, L. B. & Jetz, W. Linking global turnover of species and environments. Proc. Natl Acad. Sci. USA 105, 17836–17841 (2008).

    CAS  PubMed  Google Scholar 

  27. Shmida, A. & Wilson, M. V. Biological determinants of species diversity. J. Biogeogr. 12, 1–20 (1985).

    Google Scholar 

  28. Böhning-Gaese, K. Determinants of avian species richness at different spatial scales. J. Biogeogr. 24, 49–60 (1997).

    Google Scholar 

  29. Belmaker, J. & Jetz, W. Cross-scale variation in species richness–environment associations. Glob. Ecol. Biogeogr. 20, 464–474 (2011).

    Google Scholar 

  30. Rahbek, C. & Graves, G. R. Multiscale assessment of patterns of avian species richness. Proc. Natl Acad. Sci. USA 98, 4534–4539 (2001).

    CAS  PubMed  Google Scholar 

  31. Wang, Z., Brown, J. H., Tang, Z. & Fang, J. Temperature dependence, spatial scale, and tree species diversity in eastern Asia and North America. Proc. Natl Acad. Sci. USA 106, 13388–13392 (2009).

    CAS  PubMed  Google Scholar 

  32. Whittaker, R. J., Willis, K. J. & Field, R. Scale and species richness: towards a general, hierarchical theory of species diversity. J. Biogeogr. 28, 453–470 (2001).

    Google Scholar 

  33. Ricklefs, R. E. Intrinsic dynamics of the regional community. Ecol. Lett. 18, 497–503 (2015).

    PubMed  Google Scholar 

  34. Vázquez-Rivera, H. & Currie, D. J. Contemporaneous climate directly controls broad-scale patterns of woody plant diversity: a test by a natural experiment over 14,000 years. Glob. Ecol. Biogeogr. 24, 97–106 (2015).

    Google Scholar 

  35. Fine, P. V. A. Ecological and evolutionary drivers of geographic variation in species diversity. Annu. Rev. Ecol. Evol. Syst. 46, 369–392 (2015).

    Google Scholar 

  36. Harmon, L. J. & Harrison, S. Species diversity is dynamic and unbounded at local and continental scales. Am. Nat. 185, 584–593 (2015).

    PubMed  Google Scholar 

  37. Wiens, J. J., Pyron, R. A. & Moen, D. S. Phylogenetic origins of local-scale diversity patterns and the causes of Amazonian megadiversity. Ecol. Lett. 14, 643–652 (2011).

    PubMed  Google Scholar 

  38. Hawkins, B. A., Porter, E. E. & Diniz-Filho, J. A. F. Productivity and history as predictors of the latitudinal diversity gradient of terrestrial birds. Ecology 84, 1608–1623 (2003).

    Google Scholar 

  39. Algar, A. C., Kerr, J. T. & Currie, D. J. Evolutionary constraints on regional faunas: whom, but not how many. Ecol. Lett. 12, 57–65 (2009).

    PubMed  Google Scholar 

  40. Dunn, R. R. et al. Climatic drivers of hemispheric asymmetry in global patterns of ant species richness. Ecol. Lett. 12, 324–333 (2009).

    PubMed  Google Scholar 

  41. Araújo, M. B. et al. Quaternary climate changes explain diversity among reptiles and amphibians. Ecography 31, 8–15 (2008).

    Google Scholar 

  42. Belmaker, J. & Jetz, W. Relative roles of ecological and energetic constraints, diversification rates and region history on global species richness gradients. Ecol. Lett. 18, 563–571 (2015).

    PubMed  Google Scholar 

  43. Kreft, H. & Jetz, W. Global patterns and determinants of vascular plant diversity. Proc. Natl Acad. Sci. U.S.A. 104, 5925–5930 (2007).

    CAS  PubMed  PubMed Central  Google Scholar 

  44. Currie, D. J. & Paquin, V. Large-scale biogeographical patterns of species richness of trees. Nature 329, 326 (1987).

    Google Scholar 

  45. Francis, A. P. & Currie, D. J. Global patterns of tree species richness in moist forests: another look. Oikos 81, 598–602 (1998).

    Google Scholar 

  46. Šímová, I. et al. Global species–energy relationship in forest plots: role of abundance, temperature and species climatic tolerances. Glob. Ecol. Biogeogr. 20, 842–856 (2011).

    Google Scholar 

  47. Latham, R. & Ricklefs, R. E. Global patterns of tree species richness in moist forests: energy-diversity theory does not account for variation in species richness. Oikos 67, 325–333 (1993).

    Google Scholar 

  48. Ricklefs, R. E., Latham, R. E. & Qian, H. Global patterns of tree species richness in moist forests: distinguishing ecological influences and historical contingency. Oikos 86, 369–373 (1999).

    Google Scholar 

  49. Qian, H., Wiens, J. J., Zhang, J. & Zhang, Y. Evolutionary and ecological causes of species richness patterns in North American angiosperm trees. Ecography 38, 241–250 (2015).

    Google Scholar 

  50. Qian, H. & Ricklefs, R. E. Large-scale processes and the Asian bias in species diversity of temperate plants. Nature 407, 180–182 (2000).

    CAS  PubMed  Google Scholar 

  51. Ricklefs, R. E., Qian, H. & White, P. S. The region effect on mesoscale plant species richness between eastern Asia and eastern North America. Ecography 27, 129–136 (2004).

    Google Scholar 

  52. Lyons, S. K. & Willig, M. R. A hemispheric assessment of scale dependence in latitudinal gradients of species richness. Ecology 80, 2483–2491 (1999).

    Google Scholar 

  53. O’Brien, E. M., Field, R. & Whittaker, R. J. Climatic gradients in woody plant (tree and shrub) diversity: water-energy dynamics, residual variation, and topography. Oikos 89, 588–600 (2000).

    Google Scholar 

  54. Field, R., O’Brien, E. M. & Whittaker, R. J. Global models for predicting woody plant richness from climate: development and evaluation. Ecology 86, 2263–2277 (2005).

    Google Scholar 

  55. Brown, J. H. Macroecology (Univ. of Chicago Press, Chicago, 1995).

  56. Mutke, J. & Barthlott, W. Patterns of vascular plant diversity at continental to global scale. Biol. Skrift. 55, 521–538 (2005).

    Google Scholar 

  57. Lomolino, M. V., Riddle, B. R., Whittaker, R. J. & Brown, J. H. Biogeography (Sinauer Associates, Sunderland, 2010).

  58. Qian, H. A comparison of the taxonomic richness of temperate plants in East Asia and North America. Am. J. Bot. 89, 1818–1825 (2002).

    PubMed  Google Scholar 

  59. Crist, T. O. & Veech, J. A. Additive partitioning of rarefaction curves and species-area relationships: unifying alpha-, beta- and gamma-diversity with sample size and habitat area. Ecol. Lett. 9, 923–932 (2006).

    PubMed  Google Scholar 

  60. Svenning, J.-C. & Skov, F. Limited filling of the potential range in European tree species: limited range filling in European trees. Ecol. Lett. 7, 565–573 (2004).

  61. Jansson, R. & Davies, T. J. Global variation in diversification rates of flowering plants: energy vs. climate change. Ecol. Lett. 11, 173–183 (2007).

    PubMed  Google Scholar 

  62. Legendre, P. Spatial autocorrelation: trouble or new paradigm? Ecology 74, 1659–1673 (1993).

    Google Scholar 

  63. Dormann, C. F. et al. Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography 30, 609–628 (2007).

    Google Scholar 

  64. Dormann, C. F. Effects of incorporating spatial autocorrelation into the analysis of species distribution data. Glob. Ecol. Biogeogr. 16, 129–138 (2007).

    Google Scholar 

  65. Quintero, I. & Jetz, W. Global elevational diversity and diversification of birds. Nature 555, 246–250 (2018).

    CAS  PubMed  Google Scholar 

  66. Stein, A., Gerstner, K. & Kreft, H. Environmental heterogeneity as a universal driver of species richness across taxa, biomes and spatial scales. Ecol. Lett. 17, 866–880 (2014).

    PubMed  Google Scholar 

  67. MacArthur, R. H. & Wilson, E. O. The Theory of Island Biogeography (Princeton Univ. Press, Princeton, 1967).

  68. Carrete, M. et al. Habitat, human pressure, and social behavior: Partialling out factors affecting large-scale territory extinction in an endangered vulture. Biol. Conserv. 136, 143–154 (2007).

    Google Scholar 

  69. Randin, C. F. et al. Climate change and plant distribution: local models predict high‐elevation persistence. Glob. Change Biol. 15, 1557–1569 (2009).

    Google Scholar 

  70. White, E. P. & Hurlbert, A. H. The combined influence of the local environment and regional enrichment on bird species richness. Am. Nat. 175, E35–E43 (2010).

    PubMed  Google Scholar 

  71. Dormann, C. F. et al. co-linearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography 36, 27–46 (2013).

    Google Scholar 

  72. Rominger, A. J. et al. Community assembly on isolated islands: macroecology meets evolution. Glob. Ecol. Biogeogr. 25, 769–780 (2016).

    Google Scholar 

  73. Swenson, N. G. et al. Constancy in functional space across a species richness anomaly. Am. Nat. 187, E83–E92 (2016).

    PubMed  Google Scholar 

  74. Šizling, A. L. et al. Can people change the ecological rules that appear general across space? Glob. Ecol. Biogeogr. 25, 1072–1084 (2016).

    Google Scholar 

  75. Quintero, I., Keil, P., Jetz, W. & Crawford, F. W. Historical biogeography using species geographical ranges. Syst. Biol. 64, 1059–1073 (2015).

    PubMed  PubMed Central  Google Scholar 

  76. Arias, J. S. An event model for phylogenetic biogeography using explicitly geographical ranges. J. Biogeogr. 44, 2225–2235 (2017).

    Google Scholar 

  77. Hawkins, B. A. & Porter, E. E. Relative influences of current and historical factors on mammal and bird diversity patterns in deglaciated North America: climate, ice and diversity. Glob. Ecol. Biogeogr. 12, 475–481 (2003).

    Google Scholar 

  78. Sandel, B. et al. The influence of late quaternary climate-change velocity on species endemism. Science 334, 660–664 (2011).

    CAS  PubMed  Google Scholar 

  79. Jetz, W. & Fine, P. V. A. Global gradients in vertebrate diversity predicted by historical area-productivity dynamics and contemporary environment. PLoS Biol. 10, e1001292 (2012).

    CAS  PubMed  PubMed Central  Google Scholar 

  80. Cabral, J. S., Valente, L. & Hartig, F. Mechanistic simulation models in macroecology and biogeography: state-of-art and prospects. Ecography 40, 267–280 (2017).

    Google Scholar 

  81. Connolly, S. R., Keith, S. A., Colwell, R. K. & Rahbek, C. Process, mechanism, and modeling in macroecology. Trends Ecol. Evol. 32, 835–844 (2017).

    PubMed  Google Scholar 

  82. McGill, B. Strong and weak tests of macroecological theory. Oikos 102, 679–685 (2003).

    Google Scholar 

  83. Coelho de Souza, F. et al. Evolutionary heritage influences Amazon tree ecology. Proc. R. Soc. B 283, 20161587 (2016).

    PubMed  Google Scholar 

  84. Phillips, O. L. et al. Efficient plot-based floristic assessment of tropical forests. J. Trop. Ecol. 19, 629–645 (2003).

    Google Scholar 

  85. Ramesh, B. R. et al. Forest stand structure and composition in 96 sites along environmental gradients in the central Western Ghats of India. Ecology 91, 3118–3118 (2010).

    Google Scholar 

  86. Myers, J. A., Chase, J. M., Crandall, R. M. & Jiménez, I. Disturbance alters beta-diversity but not the relative importance of community assembly mechanisms. J. Ecol. 103, 1291–1299 (2015).

    Google Scholar 

  87. US Department of Agriculture. Forest Inventory and Analysis – Fiscal Year 2016 Business Report (US Department of Agriculture, Washington, D.C., 2016).

  88. De Natale, F. et al. Inventario Nazionale delle Foreste e dei Serbatoi Forestali di Carbonio (Ispettorato Generale del Corpo Forestale dello Stato, CRA-ISAFA, Trento, 2005).

  89. Institut national de l’information géographique et forestière. French National Forest Inventory (FNFI) (IGN, Saint-Mandé, 2017); http://inventaire-forestier.ign.fr/

  90. Abbott, I. Comparisons of spatial pattern, structure, and tree composition between virgin and cut-over jarrah forest in Western Australia. For. Ecol. Manag. 9, 101–126 (1984).

    Google Scholar 

  91. Adam, J. H. Changes in forest community structures of tropical montane rain forest on the slope of Mt. Trus Madi in Sabah, Malaysia. J. Trop. For. Sci. 13, 76–92 (2001).

    Google Scholar 

  92. Addo-Fordjour, P., Obeng, S., Anning, A. & Addo, M. Floristic composition, structure and natural regeneration in a moist semi-deciduous forest following anthropogenic disturbances and plant invasion. Int. J. Biodiv. Conserv. 1, 21–37 (2009).

    Google Scholar 

  93. Adekunle, V. A. J. Conservation of tree species diversity in tropical rainforest ecosystem of South-West Nigeria. J. Trop. For. Sci. 18, 91–101 (2006).

    Google Scholar 

  94. Ansley, S. J.-A. & Battles, J. J. Forest composition, structure, and change in an old-growth mixed conifer forest in the northern Sierra Nevada. J. Torrey Bot. Soc. 125, 297–308 (1998).

    Google Scholar 

  95. Beals, E. W. The remnant cedar forests of Lebanon. J. Ecol. 53, 679–694 (1965).

    Google Scholar 

  96. Bonino, E. E. & Araujo, P. Structural differences between a primary and a secondary forest in the Argentine Dry Chaco and management implications. For. Ecol. Manag. 206, 407–412 (2005).

    Google Scholar 

  97. Cairns, M. A., Olmsted, I., Granados, J. & Argaez, J. Composition and aboveground tree biomass of a dry semi-evergreen forest on Mexico’s Yucatan Peninsula. For. Ecol. Manag. 186, 125–132 (2003).

    Google Scholar 

  98. Cao, M. & Zhang, J. Tree species diversity of tropical forest vegetation in Xishuangbanna, SW China. Biodivers. Conserv. 6, 995–1006 (1997).

    Google Scholar 

  99. Cheng-Yang, Z., Zeng-Li, L. I. U. & Jing-Yun, F. Tree species diversity along latitudinal gradient on southeastern and northwestern slopes of Mt. Huanggang, Wuyi Mountains, Fujian, China. Biodivers. Sci. 12, 63–74 (2004).

    Google Scholar 

  100. Davis, M. A., Curran, C., Tietmeyer, A. & Miller, A. Dynamic tree aggregation patterns in a species-poor temperate woodland disturbed by fire. J. Veg. Sci. 16, 167–174 (2005).

    Google Scholar 

  101. Do, T. V. et al. Effects of micro-topographies on stand structure and tree species diversity in an old-growth evergreen broad-leaved forest, southwestern Japan. Glob. Ecol. Conserv. 4, 185–196 (2015).

    Google Scholar 

  102. Eichhorn, M. Boreal forests of Kamchatka: structure and composition. Forests 1, 154–176 (2010).

    Google Scholar 

  103. Enoki, T. Microtopography and distribution of canopy trees in a subtropical evergreen broad-leaved forest in the northern part of Okinawa Island, Japan. Ecol. Res. 18, 103–113 (2003).

    Google Scholar 

  104. Eshete, A., Sterck, F. & Bongers, F. Diversity and production of Ethiopian dry woodlands explained by climate- and soil-stress gradients. For. Ecol. Manag. 261, 1499–1509 (2011).

    Google Scholar 

  105. Fashing, P. J., Forrestel, A., Scully, C. & Cords, M. Long-term tree population dynamics and their implications for the conservation of the Kakamega Forest, Kenya. Biodivers. Conserv. 13, 753–771 (2004).

    Google Scholar 

  106. Graham, A. W. The CSIRO Rainforest Permanent Plots of North Queensland - Site, Structural, Floristic and Edaphic Descriptions (CSIRO and the Cooperative Research Centre for Tropical Rainforest Ecology and Management, Rainforest CRC, Cairns, 2006).

  107. Hirayama, K. & Sakimoto, M. Spatial distribution of canopy and subcanopy species along a sloping topography in a cool‐temperate conifer‐hardwood forest in the snowy region of Japan. Ecol. Res. 18, 443–454 (2003).

    Google Scholar 

  108. Jing-Yun, F., Yi-De, L. I., Biao, Z. H. U., Guo-Hua, L. I. U. & Guang-Yi, Z. Community structures and species richness in the montane rain forest of Jianfengling, Hainan Island, China. Biodivers. Sci. 12, 29–43 (2004).

    Google Scholar 

  109. Kohira, M., Ninomiya, I., Ibrahim, A. Z. & Latiff, A. Diversity, diameter structure and spatial pattern of trees in semi-evergreen rain forest of Langkawi island, Malaysia. J. Trop. For. Sci. 13, 460–476 (2001).

    Google Scholar 

  110. Kohyama, T. Tree size structure of stands and each species in primary warm-temperate rain forests of Southern Japan. Bot. Mag. Tokyo 99, 267–279 (1986).

    Google Scholar 

  111. Krishnamurthy, Y. L. et al. Vegetation structure and floristic composition of a tropical dry deciduous forest in Bhadra Wildlife Sanctuary, Karnataka, India. Trop. Ecol. 51, 235–246 (2010).

    Google Scholar 

  112. Lalfakawma, Sahoo, U., Roy, S., Vanlalhriatpuia, K. & Vanalalhluna, P. C. Community composition and tree population structure in undisturbed and disturbed tropical semi-evergreen forest stands of North-East India. Appl. Ecol. Env. Res. 7, 303–318 (2010).

    Google Scholar 

  113. Linder, P., Elfving, B. & Zackrisson, O. Stand structure and successional trends in virgin boreal forest reserves in Sweden. For. Ecol. Manag. 98, 17–33 (1997).

    Google Scholar 

  114. Lopes, C. G. R., Ferraz, E. M. N. & Araújo, EdeL. Physiognomic-structural characterization of dry- and humid-forest fragments (Atlantic Coastal Forest) in Pernambuco State, NE Brazil. Plant Ecol. 198, 1–18 (2008).

    Google Scholar 

  115. Lü, X.-T., Yin, J. & Tang, J.-W. Structure, tree species diversity and composition of tropical seasonal rainforests in Xishuangbanna, South-West China. J. Trop. For. Sci. 22, 260–270 (2010).

    Google Scholar 

  116. Malizia, A. & Grau, R. Liana–host tree associations in a subtropical montane forest of north-western Argentina. J. Trop. Ecol. 22, 331–339 (2006).

    Google Scholar 

  117. Maycock, F. P., Guzik, J., Jankovic, J., Shevera, M. & Carleton, J. T. Composition, structure and ecological aspects of mesic old growth Carpathian deciduous forests of Slovakia, southern Poland and the western Ukraine. Fragm. Flor. Geobot. 45, 281–321 (2000).

    Google Scholar 

  118. Nagel, A. T., Svoboda, M., Rugani, T. & Diaci, J. Gap regeneration and replacement patterns in an old-growth Fagus–Abies forest of Bosnia–Herzegovina. Plant. Ecol. 208, 307–318 (2010).

    Google Scholar 

  119. Namikawa, K., Matsui, T., Kobayashi, M., Goto, R. & Kuramoto, S. Initial establishment and regeneration processes of an outlying isolated Fagus crenata Blume forest stand in the northernmost boundary of its range in Hokkaido, northern Japan. Plant. Ecol. 207, 161–174 (2010).

    Google Scholar 

  120. Narayanan, A. & Parthasarathy, N. Biodiversity inventory of trees in a large scale permanent plot of tropical evergreen forest at Varagaliar. Anamalais, Western Ghats, India. Biodivers. Conserv. 8, 1533–1554 (1999).

    Google Scholar 

  121. Popradit, A. et al. Anthropogenic effects on a tropical forest according to the distance from human settlements. Sci. Rep. 5, 14689 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  122. Round, P., Pierce, A., Sankamethawee, W. & Gale, G. The Mo Singto forest dynamics plot, Khao Yai National Park, Thailand. Nat. Hist. Bull. Siam Soc. 57, 57–80 (2011).

    Google Scholar 

  123. Sanchez, M., Pedroni, F., Eisenlohr, P. V. & Oliveira-Filho, A. T. Changes in tree community composition and structure of Atlantic rain forest on a slope of the Serra do Mar range, southeastern Brazil, from near sea level to 1000m of altitude. Flora 208, 184–196 (2013).

    Google Scholar 

  124. Sawada, H., Ohkubo, T., Kaji, M. & Oomura, K. Spatial distribution and topographic dependence of vegetation types and tree populations of natural forests in the Chichibu Mountains, central Japan. J. Japan. Forest Soc. 87, 293–303 (2005).

    Google Scholar 

  125. Sheil, D. & Salim, A. Forest tree persistence, elephants, and stem scars. Biotropica 36, 505–521 (2004).

    Google Scholar 

  126. Shu-Qing, Z. et al. Structure and species diversity of boreal forests in Mt. baikalu, huzhong area, daxing’an mountains, northeast china. Biodivers. Sci. 12, 182–189 (2004).

    Google Scholar 

  127. Splechtna, B. E., Gratzer, G. & Black, B. A. Disturbance history of a European old-growth mixed-species forest—A spatial dendro-ecological analysis. J. Veg. Sci. 16, 511–522 (2005).

    Google Scholar 

  128. Szwagrzyk, J. & Gazda, A. Above-ground standing biomass and tree species diversity in natural stands of Central Europe. J. Veg. Sci. 18, 555–562 (2007).

    Google Scholar 

  129. Wu, X.-P., Zhu, B. & Zhao, S.-Q. Comparison of community structure and species diversity of mixed forests of deciduous broad-leaved tree and Korean pine in Northeast China. Biodivers. Sci. 12, 174–181 (2004).

    Google Scholar 

  130. Wusheng, X., Tao, D., Shihong, L. & Li, X. A comparison of tree species diversity in two subtropical forests, Guangxi, Southwest China. J. Res. Ecol. 6, 208–216 (2015).

    Google Scholar 

  131. Yamada, I. Forest ecological studies of the montane forest of Mt. Pangrango, West Java: II. Stratification and floristic composition of the forest vegetation of the higher part of Mt. Pangrango. South East Asian Studies 13, 513–534 (1976).

    Google Scholar 

  132. Yasuoka, H. The variety of forest vegetations in south-eastern Cameroon, with special reference to the availability of wild yams for the forest hunter-gatherers. Afr. Study Monogr. 30, 89–119 (2008).

    Google Scholar 

  133. Kartesz, J. T. The Biota of North America Program (BONAP) (North American Plant Atlas, Chapel Hill, 2015).

  134. Qian, H. Environmental determinants of woody plant diversity at a regional scale in China. PLoS. ONE 8, e75832 (2013).

    CAS  PubMed  PubMed Central  Google Scholar 

  135. Forzza, R. C. et al. Flora do Brazil 2020 (Jardim Botânico do Rio de Janeiro, Rio de Janeiro, 2017); http://floradobrasil.jbrj.gov.br/

  136. Liang, J. et al. Positive biodiversity-productivity relationship predominant in global forests. Science 354, aaf8957 (2016).

    PubMed  Google Scholar 

  137. Wood, S. N. Generalized Additive Models: an Introduction with R (CRC Press/Taylor & Francis Group, 2017).

  138. Carpenter, B. et al. Stan: a probabilistic programming language. J. Stat. Softw. 76, https://doi.org/10.18637/jss.v076.i01 (2017).

  139. Bürkner, P.-C. brms: an R package for Bayesian multilevel models using Stan. J. Stat. Softw. 80, https://doi.org/10.18637/jss.v080.i01 (2017).

  140. Dauby, G. et al. RAINBIO: a mega-database of tropical African vascular plants distributions. PhytoKeys 74, 1–18 (2016).

    Google Scholar 

  141. Anderson-Teixeira, K. J. et al. CTFS-ForestGEO: a worldwide network monitoring forests in an era of global change. Glob. Change Biol. 21, 528–549 (2015).

    Google Scholar 

  142. DeWalt, S. J., Bourdy, G., Chavez de Michel, L. R. & Quenevo, C. Ethnobotany of the Tacana: Quantitative inventories of two permanent plots of Northwestern Bolivia. Econ. Bot. 53, 237–260 (1999).

    Google Scholar 

  143. Enquist, B. & Boyle, B. SALVIAS—the SALVIAS vegetation inventory database. Biodivers. Ecol. 4, 288–288 (2012).

    Google Scholar 

  144. Fegraus, E. Tropical ecology assessment and monitoring network (TEAMNetwork). Biodivers. Ecol. 4, 287–287 (2012).

    Google Scholar 

  145. Oliveira-filho, A. T. NeoTropTree, Flora Arbórea da Regiāo Neotropical: um Banco de Dados Envolvendo Biogeografia, Diversidade e Conservaçāo (Universidade Federal de Minas Gerais, Belo Horizonte, 2017).

  146. Peet, R. K. et al. Vegetation-plot database of the Carolina Vegetation Survey. Biodivers. Ecol. 4, 243–253 (2012).

    Google Scholar 

  147. Peet, R. K., Lee, M. T., Jennings, M. D. & Faber-Langendoen, D. VegBank: a permanent, open-access archive for vegetation plot data. Biodivers. Ecol. 4, 233–241 (2012).

    Google Scholar 

  148. Sosef, M. S. M. et al. Exploring the floristic diversity of tropical Africa. BMC Biol. 15, 15 (2017).

    PubMed  PubMed Central  Google Scholar 

  149. Canhos, V. P. et al. Rede speciesLink: avaliação 2006 (Fapesp, São Paulo, 2006); http://splink.cria.org.br

  150. Maitner, B. S. et al. The BIEN R package: A tool to access the Botanical Information and Ecology Network (BIEN)database. Meth. Eco. Evo. 9, 373–379 (2018).

    Google Scholar 

  151. Mauri, A., Strona, G. & San-Miguel-Ayanz, J. EU-Forest, a high-resolution tree occurrence dataset for Europe. Sci. Data 4, 160123 (2017).

    PubMed  PubMed Central  Google Scholar 

  152. Borcard, D., Legendre, P. & Drapeau, P. Partialling out the spatial component of ecological variation. Ecology 73, 1045–1055 (1992).

    Google Scholar 

Download references

Acknowledgements

We thank D. Craven and I. Šímová for valuable advice, and H. Kreft, J. Coyle, R. Ricklefs, and S. Blowes for critical comments that greatly improved the manuscript. We acknowledge the support of the German Centre for Integrative Biodiversity Research (iDiv) Halle-Jena-Leipzig funded by the German Research Foundation (FZT 118).

Author information

Authors and Affiliations

  1. German Centre for Integrative Biodiversity Research (iDiv) Halle-Jena-Leipzlig, Leipzig, Germany

    Petr Keil & Jonathan M. Chase

  2. Institute of Computer Science, Martin-Luther University Halle-Wittenberg, Halle (Saale), Germany

    Jonathan M. Chase

Authors
  1. Petr Keil
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jonathan M. Chase
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

P.K. formalized the ideas, collated the data, performed the analyses, and led the writing. J.M.C. proposed the initial idea, contributed to its development, discussed the results, and contributed to the writing.

Corresponding author

Correspondence to Petr Keil.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figures 1–13, Supplementary Table 1, Supplementary Methods, Supplementary Discussion and Supplementary References

Reporting Summary

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Keil, P., Chase, J.M. Global patterns and drivers of tree diversity integrated across a continuum of spatial grains. Nat Ecol Evol 3, 390–399 (2019). https://doi.org/10.1038/s41559-019-0799-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41559-019-0799-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing