Main

As a complex adaptive system, the Earth system has multiple potential tipping elements that may approach or exceed a tipping point in response to a tiny perturbation1. Recently, others have highlighted nine climate tipping points2 that have been activated in the past decade and therefore urgent political and economic action is needed to reduce GHG emissions to prevent key tipping elements from tipping. Anthropogenic forcing is considered as one of the main factors for pushing several large-scale ‘tipping elements’ to exceed their tipping points3, which may cause abrupt and irreversible destabilizing effects on the Earth system4,5,6. Interactions between the different tipping elements may either have stabilizing or destabilizing effects on the other subsystems, potentially leading to cascades of abrupt transitions7. Following the rising awareness of a highly interconnected world, tipping cascades as possible links between tipping elements are increasingly discussed8. Using palaeoenvironmental records, ref. 9 illustrated how abrupt changes cascaded through the Earth system in the past 30 kyr. Others pointed out that tipping cascades could be formed when the global temperature reaches a threshold, affecting the trajectories of the Earth system in the Anthropocene10. However, a quantitative and systematic analysis framework on how the Earth system can be influenced by tipping elements is still lacking, especially for identifying connections among tipping elements. While preliminary studies conceptually proposed possible connections between tipping elements2,11, how these tipping elements are influenced by the mode of others and what the teleconnection paths are, are still open questions.

Here, we focus on a prominent and well-known tipping element—the Amazon Rainforest Area (ARA). It has been reported that human activities and climate change have perturbed the stability of the tropical forest–climate equilibrium, resulting in extreme losses of tropical forests and biodiversity12. A recent empirical study suggests that the observed tropical forest fragmentations, including in the Americas, Africa and Asia–Australia, are approaching their tipping points13. Particularly striking is the deforestation in the Amazon—the world’s largest rainforest, which is home to nearly a quarter of the world’s terrestrial species. Southeast Amazonia has even become a net source of carbon emission during the dry season because of the deforestation and climate change14. It was recently pointed out that more than three-quarters of the Amazon rainforest has been losing resilience since the early 2000s, consistent with the approach to a critical transition15. The Sixth Assessment Report of IPCC highlighted that continued deforestation and a warming raise the probability that the Amazon will cross a tipping point into a dry state5. However, global influences of rainforest dieback in the Amazon are still little known.

In the present study, we construct a series of dynamical and physical climate networks16,17,18,19,20,21,22, based on the global near-surface air temperature field, to systematically study the global impacts of the ARA. The directed links from the ARA (Fig. 1, location labelled 6) to regions outside the ARA are defined as ‘in’-links. The in-weighted climate network enables us to obtain a map of the global impacts of ARA, in particular, to study the impacts in specific regions, such as other tipping elements. In particular, we uncover that there exists a robust negative teleconnection between the ARA and the Tibetan Plateau (TP) (Fig. 1, location labelled 10), known as the third pole of the Earth23. We further explore the potential propagation pathway of the ARA–TP teleconnection. This work provides a concise and systematic framework to investigate the potential teleconnection among the tipping elements and can potentially be used to predict the abrupt changes caused by the tipping cascading in the Earth systems.

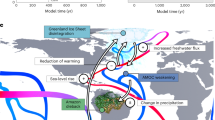
Fig. 1: Schematic view of the tipping elements of the Earth climate system, their connectivity and teleconnections.
figure 1

The numbered symbols show the potential tipping elements in the Earth system. The dashed yellow lines show the possible connections between these tipping elements2 and the solid red lines show teleconnection uncovered in this article. The arrows show the direction of the influence.

Full size image

Strongly localized planetary impact pattern of the ARA

To reveal the global impact of the ARA, we divide the nodes of climate networks into two subsets. One subset includes the nodes within the ARA (1,374 nodes, 12∘ N to 35∘ S, 30° W to 90∘ W land area) and the other contains the nodes outside the ARA (63,786 nodes). To quantify the overall impact of the ARA, for a given outside node j, we define its in-weight (IN(Cj)) and in-strength (IN(Wj)) as the sum of the weights and strengths of all in-links (Methods). A larger (smaller) positive (negative) value of IN(Cj) and IN(Wj) indicate stronger (weaker) warming (cooling) due to the influence of the ARA; likewise, out-weights (OUT(Cj) and OUT(Wj)) are introduced to quantify the overall impacts to the ARA. We present the influence pattern between the ARA and the outside area in Supplementary Fig. 1a,b for the past 40 yr (1979–2018). We find that some regions such as the Mid-Atlantic, the Arctic and the Indian Ocean, either by warming or cooling, are identified by relatively higher in-weights (Supplementary Fig. 1a). It has been reported that the climate variability in the ARA is significantly affected by the phase of El Niño/Southern Oscillation (ENSO)24; this influence is also confirmed by the high intensity of the tropical Pacific region in out-weight distributions (Supplementary Fig. 1b). In particular, we find that the Niño 3.4 region shows a strongly positive influence on the ARA.

There exist strong connections between ARA and ENSO. To further address whether the influence pattern of ARA varies between ENSO periods and normal years, we analyse and compare the global distributions of the total in-degrees IN(N), in-weights IN(C) and in-strengths IN(W), among one typical El Niño year (1997), one typical La Niña year (1998) and one normal year (1996). The result is shown in Fig. 2. We find that during El Niño and La Niña events, the overall global area that is influenced by the ARA becomes smaller, whereas the impacts in these more limited ranges become stronger. This enhanced impact in localized regions is demonstrated in Fig. 2a–f, which compares the global distributions of the normal year in Fig. 2g–i. This strongly localized planetary impact pattern of the ARA is robust during ENSO period, which is supported by more examples and quantitative analysis (Supplementary Figs. 2 and 3).

Fig. 2: The different influence modes of the ARA for ENSO years and a normal year.
figure 2

IN(C) (a. an El Niño year, d. a La Niña year and g. a normal year), IN(W) (b. an El Niño year, e. a La Niña year and h. a normal year) and IN(N) (c. an El Niño year, f. a La Niña year and i. a normal year) show a more localized and higher intensity pattern in the El Niño (a–c) and La Niña (d–f) years than in the normal year (g–i).

Source data

Full size image

Negative teleconnection between ARA and TP

The regions of localized activity vary from one year to another. Next, we study the variability of the regions that are influenced by ARA. For each year, we consider the high-intensity nodes, that is, with the value (absolute value) of the in-degree (negative in-weight) higher than 90% nodes (negative nodes). We then define the frequency of the nodes with high intensity during the past 40 yr from 1979 to 2018 as F(N) and F(C) (Methods). The results are shown in Fig. 3a,b for F(N) and F(C), respectively. Higher values indicate stronger and more persistent impacts of ARA. Remarkably, we find that the intensity of the nodes within the TP region is high for both F(N) and F(C) and the spatial pattern of these nodes agrees well with the cartographic boundary (the dashed yellow lines in the right panels of Fig. 3a,b) and shape of the TP. A similar pattern can also be obtained from the F(W) (Supplementary Fig. 4), which serves as a cross-check of the result of F(C). A typical cross-correlation function of two nodes, one in ARA and the other in TP, is presented in Supplementary Fig. 5, which indicates a significant negative teleconnection. Besides the TP, we also observe that there exist strong negative connections between the ARA and the West Antarctic, which is known as a tipping element2.

Fig. 3: Stable negative teleconnection between the ARA and the TP.
figure 3

a, The spatial distribution of F(N) and, b, F(C), depicting the areas influenced by ARA in the past 40 yr (1979–2018). The nodes within TP show high intensity and the spatial pattern is perfectly characterized by the cartographic boundary of the TP (the dashed orange line). c, The crosses depict the nodes’ signals F(N) and, d, F(C) passing the hypothesis test. The 95th percentile of the F(N) and F(C) distributions of the NULL model is considered as the significant threshold. The nodes in the TP with a higher intensity than the threshold are labelled by the crosses. Here, the red colour indicates F(N) and the blue colour stands for F(C).

Source data

Full size image

To demonstrate that these results are not accidental, we analysed randomized versions of F(N) and F(C), which we obtained by reshuffling the temperature records at each site 100 times. This way, we destroy the correlations between different nodes (one example of the cross-correlation results of this NULL model can be found in Supplementary Fig. 6c,d). Our results, shown in Fig. 3c,d, indicate that the values of F(N) and F(C) for the nodes in the TP region have a 95% confidence level compared with the NULL model.

Robust propagation pathway of ARA and TP teleconnection

Teleconnections describe remote connections between components of the complex climate system and reflect the transportation of energy or materials on global scale25. The great-circle distances of teleconnections are typically thousands of kilometres. In the following, we will identify the actual path of the teleconnection between the ARA and the TP by using the climate network analysis. We choose 726 latitude–longitude grid points as climate network nodes19, such that the globe is covered approximately homogeneously. We follow ref. 26 and detect a minimal total cost function of the direct links (Methods) from the ARA to the TP. We show a potential propagation path for this teleconnection in Fig. 4a and find that it can be roughly divided into three parts. The first part is from the centre of South America to the south of Africa, the second one is from the south of Africa to the Middle East and the last part is from the Middle East to the TP. The path length is close to 20,000 km (the great-circle distance between the ARA and TP is ~15,000 km). From a meteorological perspective, this path can be well explained by the main atmospheric and oceanic circulation.

Fig. 4: The propagation pathway of the teleconnection between the ARA and the TP.
figure 4

a, The large red and blue dots depict the starting and ending nodes and the small dots are the network nodes passed along the path. The black arrow indicates the propagation direction. The potential meteorological interpretation of this path is described by three parts, corresponding to the dashed lines with different colours. b–e, The robust propagation pathway under global warming conditions. By comparing the pathway in the first (b,d) and the last (c,e) 40 yr for this century in CMIP5 (b,c) and CMIP6 (d,e) datasets, we find that the overall pattern is quite stable across most models.

Source data

Full size image

On the one side, the orography of the eastern coast of the South American continent is prone to the formation of an anticyclone at mid-latitude due to the interaction with mid-latitude westerlies27. The anticyclonic circulation produces and brings warm winds from the east coast of South America to the South of Africa (~30∘ S). On the other side, there is an intertropical convergence zone that controls the African monsoon driving the wind from south to north of Africa in this regime28. Finally, the physical mechanism of the path from the Middle East to the TP may be linked to the northern hemispheric middle latitude westerlies29.

To examine the data dependence of the path, we perform the same climate network-based analysis with different reanalysis datasets, that is, the ERA5 with 2 m surface temperature and the NCEP/NCAR reanalysis with 1,000 hPa, 2 m surface temperature dataset. All results are presented in Supplementary Fig. 7 and suggest that the propagation pathway of the teleconnection between the ARA and TP is independent of datasets. The robustness is estimated by comparing with the second optimal path, as shown in Supplementary Fig. 8. We find that the second optimal path is close to the first optimal path, supporting that the propagation pathway is robust. Furthermore, various starting and ending nodes within ARA and TP have been selected by using the same analysis and we find that the optimal pathway between ARA and TP is still very stable (Supplementary Fig. 9).

Anthropogenic climate change has led to a widespread shrinking of the cryosphere, rising global mean sea levels, an increasing number of tropical cyclones and associated cascading impacts30. A critical question, then, is how climate change could affect the nature of the path of this teleconnection? We thus investigate the response of the teleconnection path to global warming by using the Coupled Model Intercomparison Project Phase 5 (CMIP5) and Phase 6 (CMIP6) models under the RCP8.5 (approximately equivalent to the Shared Socioeconomic Pathway (SSP) 5–8.5) emission scenario from 2006 (CMIP5) and 2016 (CMIP6) to 2100. We chose 15 CMIP5 models and 15 CMIP6 models and summarize the details in Supplementary Tables 1 and 2. To identify the response of the teleconnection pathway under the global warming condition, for simplicity but without loss of generality, we compare, in Fig. 4b–e, the path from ARA to TP for the first and last 40 years of the twenty-first century, that is, 2016–2056 (2006–2046 for CMIP5 datasets) versus 2060–2100. Interestingly, we observe that the overall pattern of this teleconnection pathway from the ARA to TP is quite stable across most models. Additionally, we calculate the propagation time by summing the time lags for each step and find that the time delay is ~15 d for most models (Supplementary Fig. 10). Besides the TP, the high-intensity nodes within the West Antarctic Ice Sheet (WAIS) in Fig. 3b indicate the existence of stable negative teleconnection between these two well-known tipping elements, ARA and WAIS. For more discussion about the propagation path and potential mechanism of this teleconnection see Supplementary Figs. 11 and 12.

Synchronization of extreme climate events

Since our results indicate that the teleconnection path is not affected by climate change (Fig. 4), one key issue is how do the climate variabilities in between the ARA and TP synchronize in the presence of global warming? In the following, we focus on the synchronization of various extreme climate events between ARA and TP. We first analyse the global change by the fraction of days with above average temperature (TXgt50p) in every two decades (2021–2040, 2041–2060, 2061–2080 and 2081–2100) under four SSPs and notice a clear spatial synchronization of this indicator in the Amazon and the TP for all SSPs. Both the Amazon and the TP are the most sensitive areas globally in terms of the increase of TXgt50p, as shown in Supplementary Fig. 13. Multimodel ensemble were applied here, based on six models from Global Producing Centres for long-range forecasts designated by the World Meteorological Organization, which has been confirmed to have higher simulation capacity than that of each model31. To quantify the spatial synchronization of these two regions, we performed Pearson’s correlation analyses on the TXgt50p values. Surprisingly, we find that the Pearson’s r reaches 0.92 for the TXgt50p in the Amazon and the TP, illustrating a significant positive correlation between these two regions. Similarly, we tested the other major temperature-related indicators, TMge10 (number of days with daily mean temperature equal to or above 10 ∘C) and TNn (the monthly minimum of Tmin). Strong positive correlation exists between the TP and Amazon region for both TMge10 (r = 0.70) and TNn (r = 0.74). Meanwhile, a strong or moderate negative correlation exists in precipitation-related indicators, such as Prcptot (−0.54; Supplementary Fig. 14), R20mm (−0.50; Supplementary Fig. 15) and Rx5day (−0.20, Supplementary Fig. 16). These three indicators represent annual total precipitation, number of days with precipitation above 20 mm and the maximum 5 d consecutive precipitation, respectively. These results support the finding that there exists some kind of physical connection between these two far-reaching regions. It is noticed that all precipitation-related indicators show a negative correlation, while temperature-related indicators show a positive correlation between the TP and Amazon.

The TP is operating close to a tipping point

The TP has attracted much attention due to its unique geological structure, irreplaceable role in global water storage and impact on the global climate system. Numerous literatures have shown that the warming trend in recent decades at the TP is several times faster than the global average and is similar to the trend of the arctic region23. Projections have shown that this amplification of warming will continue under global warming, thereby increasing the occurrence of climate extremes32. Snow cover is a comprehensive indicator of the mean conditions of temperature and precipitation for an area. Especially for the TP, the snow cover can persist during all seasons over the high elevation area and serve as a vital water source for the surrounding countries. In particular, snow cover variability is an integrated indicator of climate change33 and thus can be a sensitive parameter reflecting the state change of the TP under global warming. In the following, we will detect the early warning signals based on the snow cover and reveal that the TP has been losing stability and approaching a tipping point since 2008.

The ‘critical slowing down’ (CSD) phenomenon has been suggested as one of the most important indicators of whether a dynamical system is losing stability and getting close to a critical threshold4,34. The loss of stability (defined as the return rate from perturbation) can be detected by increases in the lag-1 autocorrelation (AR(1)) coefficients 35 and detrended fluctuation analysis (DFA) exponents36. These methods have been applied to quantify the CSD and anticipate tipping points37,38. Here, we focus on the temporal evolution of AR(1) coefficients and DFA exponents based on the time series of the snow cover fraction (SCF) over the whole TP area during 1990–2020 (Methods). The seasonal and trend decomposition based on Loess (STL) method has been used to obtain the detrended time series and avoid false alarms (Methods and Fig. 5a). By shifting a sliding 10 yr window and calculating the AR(1) coefficients (with 1 d time unit) and DFA exponents for every step, we can retrieve the temporal changes of the AR(1) coefficients (Fig. 5b) and DFA exponents (Fig. 5c) in the past 31 yr (1990–2020). The time series of the AR(1) coefficient shows a substantial increase over time, particularly since 2008 (the red line in Fig. 5b). The DFA exponent has also been increasing since 2008 and is consistent with the AR(1) coefficient, as shown in Fig. 5c. We quantify the increasing tendency of AR(1) and DFA exponents by the Kendall rank correlation coefficient τ (Methods), with 0.95 and 0.86, respectively. Both results of the Kendall τ support an obvious increase for AR(1) and DFA, which implies that the snow cover in TP has been approaching a tipping point since 2008.

Fig. 5: The early warning indicators in TP snow cover data show CSD since 2008.
figure 5

a, The time series of the SCF over the whole TP. Grey line shows the original data, black line shows the trend component and seasonal cycle component from the STL decomposed. b, The time series of AR(1) coefficient with 1 d time unit. c, The time series of the DFA exponent. AR(1) coefficient and DFA exponent are calculated using a sliding window with a length of 10 yr. The black horizontal arrow represents the length of the moving window and the vertical black dashed line indicates the time stamp from which the early warning measures are calculated. The line colour depicts the different tendency of the time series. The Kendall τ values of the AR(1) coefficient and DFA exponent since 2008 are 0.805 (P < 0.0001) and 0.926 (P < 0.0001), respectively. The P value is obtained by two-sided hypothesis test.

Source data

Full size image

Discussion

The persistent warming fuelled by anthropogenic GHG emissions could push parts of the Earth system—tipping elements—into abrupt or irreversible changes, from collapsing ice sheets and thawing permafrost, to shifting monsoons and forest dieback2. These climatic changes thus influence the nature of societies and the performance of economies39. Most importantly, possible connections and cascading dynamics between different tipping elements have been proposed. However, a method to quantify the connections or teleconnections among possible tipping elements was lacking. To fill the gap, here, we have developed a network-based framework to reveal the global impact of a widely pronounced tipping element—the ARA. We found that there is a planetary pattern of strongly localized impacts of the ARA and some specific regions, such as the TP and West Antarctic, are strongly and persistently influenced by the ARA. A robust teleconnection propagation path has been identified between the Amazon and TP. We proposed a possible physical mechanism underlying this path and associated it with the combination of: (1) the South Atlantic High, (2) the intertropical convergence zone and (3) the northern hemispheric middle latitude westerlies. The high degree of synchronization of the extreme events in the ARA and TP supports the existence of this teleconnection. Moreover, we provided strong support that the snow cover in TP (CDS phenomenon) has been losing stability and is operating close to a tipping point. We thus provided evidence that the TP, which was previously overlooked, should play an extremely important role as a component in the exhaustive list of tipping elements1.

Interactions and teleconnections among tipping elements potentially lead to cascades of abrupt transitions. In particular, in the context of climate change, disaster phenomena such as floods, droughts and sea level rises have become more frequent and threatening. Thus, global, national and regional preparedness and response to extreme weather are facing challenges. Climate adaptation failure has gained the greatest concern globally. Especially, the systemic risk induced by the interdependency among systems and cascading of adverse impact is the emerging key for climate adaptation. Moreover, developing topological invariants based on network theory, such as, k-core, as a predictor of climate tipping points and the corresponding collapse phenomena40, can help engaging more stakeholder groups to perform early actions to reduce tipping points-related damages. Our framework based on network theory provides a potential path to understand the linkage of tipping elements of the complex Earth system, which is particularly important for a systemic risk-informed global governance and to improve understanding of tipping points.

Methods

Data

Our climate network is based on the global hourly near-surface (1,000 hPa) air temperature data from the ERA5 reanalysis dataset41 produced by the European Centre for Medium-Range Weather Forecast. The reason we focus on the surface temperature field is that it is the most commonly used for global warming-related discussions. The original spatial resolution of the ERA5 dataset is 0.25∘ × 0.25∘. We then transform the dataset to a resolution of 1∘ × 1∘ by taking one value out of every four original data points and select the temperature at 00:00 as the daily temperature value, resulting in 365 measurements for each of the resulting 360 × 181 = 65,160 nodes for every year (in leap years we exclude 29 February, thus all years have the same length). The dataset spans the time period from January 1979 to December 2019. To avoid the strong effect of seasonality, we subtract the calendar day’s mean from the time series of each node. The analysis of influence patterns of the ARA is based on a sequence of networks, each constructed from a time series that spans one year (the data in 2019 has been used for the time lag of the correlation calculation, so the networks cover 40 yr, from 1979 to 2018).

To test whether the optimal pathway is independent of the specific dataset, we also use surface air temperature reanalysis data from ERA5, 1,000 hPa air temperature reanalysis data (2.5∘ × 2.5∘) from NCEP/NCAR and surface temperature reanalysis data (2.5∘ × 2.5∘) from NCEP/NCAR. These datasets span the time period from January 1979 to December 2019.

We use a large set of climate models simulations from CMIP6 and CMIP5 to test the robustness of the teleconnection pathway. Because of the different model resolutions, we apply a bilinear interpolation method to obtain new datasets with the same resolution of 2.5∘ × 2.5∘. The outputs from CMIP5 were forced by representative concentration pathway 8.5 (RCP8.5), covering a period from 2006 to 2100. The outputs from CMIP6 were forced by SSP 5–8.5, covering a period from 2016 to 2100. The variables of ta (air temperature) and tas (near-surface atmospheric temperature) are used here. The detailed information of these datasets can be found in Supplementary Tables 1 and 2.

Climate network construction

The nodes are divided into two subsets. One subset includes the nodes within the ARA (1,374 nodes) and the other the nodes outside the ARA (63,786 nodes). The links are constructed from the cross-correlation between two nodes from the different subsets. The cross-correlation values between the two time series of 365 d are defined by:

$${C}_{ij}^{y}(\sigma )=\frac{\langle {T}_{i}(d){T}_{j}(d+\sigma )\rangle -\langle {T}_{i}(d)\rangle \langle {T}_{j}(d+\sigma )\rangle }{\sqrt{\langle {({T}_{i}(d)-\langle {T}_{i}(d)\rangle )}^{2}\rangle }\times \sqrt{\langle {({T}_{j}(d+\sigma )-\langle {T}_{j}(d+\sigma )\rangle )}^{2}\rangle }}$$
(1)

where σ ∈ [0, σmax] is the time lag, with σmax = 200 d, y represents the starting year of this time series and \({C}_{i,j}^{y}(-\sigma )\equiv {C}_{j,i}^{y}(\sigma )\). Therefore, we can achieve 2σmax + 1 different cross-correlation values for every two nodes in one year. We then identify the maximum absolute value of this cross-correlation function and denote the corresponding time lag of this value as \({[{\sigma }_{0}]}_{i,j}^{y}\). The direction of each link is decided by the sign of σ0. When the time lag is positive (\({[{\sigma }_{0}]}_{i,j}^{y} > 0\)), the direction of the link is from i to j; when the time lag is negative, however, the direction is from j to i. The link weights are determined by \({C}_{i,j}^{y}({\sigma }_{0})\) and we can also define the strength of the link \({W}_{i,j}^{y}\) as:

$${W}_{i,j}^{y}=\frac{{C}_{i,j}^{y}({\sigma }_{0})-\,{{\mbox{mean}}}({C}_{i,j}^{y}(\sigma ))}{{{\mbox{std}}}\,({C}_{i,j}^{y}(\sigma ))}$$
(2)

where ‘mean’ and ‘std’ are the mean and s.d. of the cross-correlation function, respectively. We construct networks based on both \({C}_{i,j}^{y}({\sigma }_{0})\) and \({W}_{i,j}^{y}\).

The in- and out-degree of each node can be calculated by \({I}_{j}^{y}={\sum }_{i}{{{{A}}}}_{i,j}^{y}\), \({O}_{j}^{y}={\sum }_{i}{{{{A}}}}_{j,i}^{y}\), respectively. The adjacency matrix of this network is \({{{{A}}}}_{i,j}^{y}\) and it is defined as:

$${{{{A}}}}_{i,j}^{y}=(1-{\delta }_{i,j})H({[{\sigma }_{0}]}_{i,j}^{y})$$
(3)

where H(x) is the Heaviside step function (H(x ≥ 0) = 1 and H(x < 0) = 0). Furthermore, to describe the impact of the ARA on the global, we define the total in-degree of the node j outside the ARA as the number of its in-links, the in-weights as the sum of the weights of its in-links and the in-link strength as the sum of the strengths of its in-links:

$${{{\rm{IN}}}}({N}_{j}^{y})=\mathop{\sum}\limits_{i\in \,{{\mbox{ARA}}}\,}{{{{A}}}}_{i,j}^{y},$$
(4)
$${{{\rm{IN}}}}({C}_{j}^{y})=\mathop{\sum}\limits_{i\in \,{{\mbox{ARA}}}\,}{{{{A}}}}_{i,j}^{y}{C}_{i,j}^{y}({\sigma }_{0}),$$
(5)
$${{{\rm{IN}}}}({W}_{j}^{y})=\mathop{\sum}\limits_{i\in \,{{\mbox{ARA}}}\,}{{{{A}}}}_{i,j}^{y}{W}_{i,j}^{y}.$$
(6)

The spatial distributions of \(\,{{\mbox{IN}}}\,({C}_{j}^{y})\) and \(\,{{\mbox{IN}}}\,({W}_{j}^{y})\) show the influence pattern of the ARA on the globe for a regarded year. Larger (smaller) positive (negative) values reflect stronger (weaker) warming (cooling) due to the impact of the ARA. In the same way, we can define out-degree, out-weights and out-strength to describe the impact of the outside world for the nodes in ARA:

$${{{\rm{OUT}}}}({N}_{i}^{y})=\mathop{\sum}\limits_{j\notin \,{{\mbox{ARA}}}\,}{{{{A}}}}_{j,i}^{y},$$
(7)
$${{{\rm{OUT}}}}({C}_{i}^{y})=\mathop{\sum}\limits_{j\notin \,{{\mbox{ARA}}}\,}{{{{A}}}}_{j,i}^{y}{C}_{j,i}^{y}({\sigma }_{0}),$$
(8)
$${{{\rm{OUT}}}}({W}_{i}^{y})=\mathop{\sum}\limits_{j\notin \,{{\mbox{ARA}}}\,}{{{{A}}}}_{j,i}^{y}{W}_{j,i}^{y}.$$
(9)

Filtering nodes from the network

To extract the stable influenced region in the past 40 yr, we removed low-intensity nodes from the network. Since ENSO causes variation in the influence intensity, the links in a normal year are commonly weaker than those in an ENSO year. For this reason, a fixed threshold will remove most of the nodes in normal years. Therefore, we set an annually changing threshold, determined by the top 10% of signal intensity distribution in the current year. Besides, the nodes near the ARA always have a high positive link-weight, which will offer us trivial results after filtering. To avoid this, we focus on finding the regions with stable negative teleconnection to the ARA.

According to the sign of \(\,{{\mbox{IN}}}\,({C}_{j}^{y})\), we divide the nodes outside the ARA into two subgroups: one subset includes the nodes with positive \(\,{{\mbox{IN}}}\,({C}_{j}^{y})\), assigned as \({N}_{+}^{y}\); another subset includes the nodes with negative \(\,{{\mbox{IN}}}\,({C}_{j}^{y})\), assigned as \({N}_{-}^{y}\). To find remarkable negatively influenced nodes, we set a threshold to select:

$${T}_{j,-}^{y}=\left\{\begin{array}{ll}1,\quad &\mathrm{abs}(\mathrm{IN}({C}_{j}^{y}))\ge \mathrm{abs}({C}_{-}^{y})\\ 0,\quad &\mathrm{abs}(\mathrm{IN}({C}_{j}^{y})) < \mathrm{abs}({C}_{-}^{y})\end{array}\right.$$
(10)

where \({C}_{-}^{y}\) is determined by the intensity of \(\,{{\mbox{IN}}}\,({C}_{j}^{y})\) in the top 10% negative strength part in this year. \({T}_{j,-}^{y}=1\) means that the intensity of the negative connection between node j and ARA is stronger than of 90% of negatively influenced nodes in this year. Therefore, we can count the number of years for the node j with top 10% negative in-weight during the past 40 yr:

$$F({C}_{j})=\mathop{\sum}\limits_{y}{T}_{j,-}^{y}.$$
(11)

Similarity, F(Wj) can be obtained from the negative part of \(\,{{\mbox{IN}}}\,({W}_{j}^{y})\). Value \(\,{{\mbox{IN}}}\,({N}_{j}^{y})\) is a positive number defined as the in-degree of node j, which cannot be divided into a positive part and a negative part. Therefore, \(F({N}_{j}^{y})\) is obtained from the top 10% of the entire \(\,{{\mbox{IN}}}\,({N}_{j}^{y})\). The distributions of F(Nj), F(Cj) and F(Wj) reflect the spatial distribution for the nodes that suffered persistent impact from the ARA.

Optimal path finding

We perform the shortest path method of complex networks to identify the optimal paths in our climate networks. We select 726 nodes from the dataset to construct cross-correlation climate networks and thus all nodes can approximately equally cover the globe. The distance between neighbouring nodes is around 830 km. The cost value for each link is defined as \(1/| {W}_{i,j}^{y}|\) to make sure the optimal path will prefer to pass the link with high significance26. The Dijkstra algorithm42 was used to determine the directed optimal path between nodes i and j with the following constraints: (1) the distance for every step is shorter than 1,000 km and (2) link time delay σ0 ≥ 0. The first constraint is used to identify the significant long-distance connections and the second constraint ensures that all steps have the same directions.

Critical slowing down analysis

Our CSD analysis for the TP is based on a long-term advanced very high resolution radiometer snow cover extent dataset43 from the Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences. The dataset has a spatial resolution of 5 km and a daily temporal resolution. Here, we consider the data of the period from 1990 to 2020. To focus on changes in the snow cover of the whole TP, we use the time series of SCF to measure the CSD indicators. The SCF of the whole TP is calculated by:

$${r}_{\mathrm{tp}}(t)=\frac{{n}_{\mathrm{sc}}(t)}{{n}_{0}},$$
(12)

where n0 = 98,549 and nsc(t) are the number of grid boxes and the number of snow-covered grid boxes in the TP, respectively.

To avoid false alarms, we use the STL method to filter out long-term trends and achieve stationarity4,38. An STL function from Python has been used in this research to split rtp(t) into three parts, an overall trend, a repeating annual cycle and a remaining residual. The remaining residual (shown in Supplementary Fig. 17) is used in our analysis.

The lag-1 autocorrelation

The AR(1) is a robust indicator for providing an early warning signal for impending bifurcation-induced transitions and has been widely used7,15. We measure our AR(1) coefficients on the basis of the residual component of the decomposed snow cover daily time series. To decrease the noise fluctuations, 30 d average is applied. The time series of the AR(1) coefficient is obtained by a sliding time window with a length of 10 yr.

Detrended fluctuation analysis

The DFA is another widely used tool for detecting the increase in memory caused by the CSD37, which can provide a useful cross-check of AR(1) (ref. 4). For a time series with long-range temporal correlations, its fluctuation function, F(n), can be characterized by a scaling exponent36

$$F(n) \sim {n}^{\alpha }$$
(13)

where n is the window length and α is the DFA scaling exponent. Here, \(F(n)=\sqrt{\frac{1}{n}\mathop{\sum }\nolimits_{t = 1}^{n}{({X}_{t}-{Y}_{t}^{z})}^{2}}\), where \({X}_{t}=\mathop{\sum }\nolimits_{i = 1}^{t}({x}_{i}-\langle x\rangle )\) is the cumulative sum of the time series and \({Y}_{t}^{z}\) is the fitted polynomial function, z stands for the polynomial order (here, we chose z = 2). F(n) is obtained by dividing the time series into [L/n] non-overlapping time intervals of length n. The DFA exponent α is calculated as the slope of the linear fit to the log–log graph of F(n) versus n, for 10 ≤ n ≤ 1,000. The time series of DFA exponent α is obtained by a sliding time window with length 10 yr.

We calculate the temporal trends of AR(1) coefficient and DFA exponent α by estimating the non-parametric Kendall rank correlation (τ). Kendall τ is a statistical tool to measure the association between the variable and time. The τ = 1 or −1 implies that the time series is always increasing or decreasing; τ = 0 means no overall trend. To test the robustness of the AR(1) and DFA analysis, we also vary the length of the sliding time window. The result with an alternatively 8 yr time window is shown in Supplementary Fig. 18 and we still see the same increase in AR(1) coefficient and DFA exponent.