Abstract
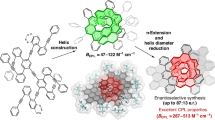
The [n]cycloparaphenylenes ([n]CPPs)—n para-linked phenylenes that form a closed-loop—have attracted substantial attention due to their unique cyclic structure and highly effective para-conjugation leading to a myriad of fascinating electronic and optoelectronic properties. However, their strained topology prevents the π-extension of CPPs to convert them either into armchair nanobelts or planarized CPP macrocycles. Here we successfully tackle this long-standing challenge and present the bottom-up synthesis and characterization of atomically precise in-plane π-extended [12]CPP on Au(111) by low-temperature scanning probe microscopy and spectroscopy combined with density functional theory. The planar π-extended CPP is a nanographene with an all-armchair edge topology. The exclusive para-conjugation at the periphery yields delocalized electronic states and the planarization maximizes the overlap of p orbitals, which both reduce the bandgap compared to conventional CPPs. Calculations predict ring currents and global aromaticity in the doubly charged system. The intriguing planar ring topology and unique electronic properties make planar π-extended CPPs promising quantum materials.

This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
Data supporting the findings of this study are available in the article, the Extended Data and Supplementary Information. DFT-calculated structures are provided as Supplementary Data files. Source data are provided with this paper.
References
Jasti, R., Bhattacharjee, J., Neaton, J. B. & Bertozzi, C. R. Synthesis, characterization and theory of [9]-, [12]- and [18]cycloparaphenylene: carbon nanohoop structures. J. Am. Chem. Soc. 130, 17646–17647 (2008).
Leonhardt, E. J. & Jasti, R. Emerging applications of carbon nanohoops. Nat. Rev. Chem. 3, 672–686 (2019).
Segawa, Y. et al. Concise synthesis and crystal structure of [12]cycloparaphenylene. Angew. Chem. Int. Ed. 50, 3244–3248 (2011).
Lewis, S. E. Cycloparaphenylenes and related nanohoops. Chem. Soc. Rev. 44, 2221–2304 (2015).
Guo, Q.-H., Qiu, Y., Wang, M.-X. & Fraser Stoddart, J. Aromatic hydrocarbon belts. Nat. Chem. 13, 402–419 (2021).
Golling, F. E. et al. π-extended [12]cycloparaphenylenes: from a hexaphenylbenzene cyclohexamer to its unexpected C2-symmetric congener. Chem. Sci. 6, 7072–7078 (2015).
Solomon, G. C., Herrmann, C., Hansen, T., Mujica, V. & Ratner, M. A. Exploring local currents in molecular junctions. Nat. Chem. 2, 223–228 (2010).
Guédon, C. M. et al. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 7, 305–309 (2012).
Piquero-Zulaica, I. et al. Electronic structure tunability by periodic meta-ligand spacing in one-dimensional organic semiconductors. ACS Nano 12, 10537–10544 (2018).
Toriumi, N., Muranaka, A., Kayahara, E., Yamago, S. & Uchiyama, M. In-plane aromaticity in cycloparaphenylene dications: a magnetic circular dichroism and theoretical study. J. Am. Chem. Soc. 137, 82–85 (2015).
Taber, B. N. et al. Quantum confinement of surface electrons by molecular nanohoop corrals. J. Phys. Chem. Lett. 7, 3073–3077 (2016).
Li, H. et al. Probing the deformation of [12]cycloparaphenylene molecular nanohoops adsorbed on metal surfaces by tip-enhanced Raman spectroscopy. J. Chem. Phys. 153, 244201 (2020).
Clair, S. & de Oteyza, D. G. Controlling a chemical coupling reaction on a surface: tools and strategies for on-surface synthesis. Chem. Rev. 119, 4717–4776 (2019).
Held, P. A., Fuchs, H. & Studer, A. Covalent-bond formation via on-surface chemistry. Chem. Eur. J. 23, 5874–5892 (2017).
Wang, T. & Zhu, J. Confined on-surface organic synthesis: strategies and mechanisms. Surf. Sci. Rep. 74, 97–140 (2019).
Talirz, L., Ruffieux, P. & Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 28, 6222–6231 (2016).
Kaiser, K. et al. An sp-hybridized molecular carbon allotrope, cyclo[18]carbon. Science 365, 1299–1301 (2019).
Haags, A. et al. Kekulene: on-surface synthesis, orbital structure and aromatic stabilization. ACS Nano 14, 15766–15775 (2020).
Su, J. et al. On-surface synthesis and characterization of [7]triangulene quantum ring. Nano Lett. 21, 861–867 (2021).
Di Giovannantonio, M. et al. Large-cavity coronoids with different inner and outer edge structures. J. Am. Chem. Soc. 142, 12046–12050 (2020).
Fan, Q. et al. Surface-assisted organic synthesis of hyperbenzene nanotroughs. Angew. Chem. Int. Ed. 52, 4668–4672 (2013).
Fan, Q. et al. On-surface synthesis and characterization of a cycloarene: C108 graphene ring. J. Am. Chem. Soc. 142, 894–899 (2020).
Papaianina, O. et al. Synthesis of rationally halogenated buckybowls by chemoselective aromatic C−F bond activation. Angew. Chem. Int. Ed. 56, 4834–4838 (2017).
Fan, Q. et al. On-surface pseudo-high-dilution synthesis of macrocycles: principle and mechanism. ACS Nano 11, 5070–5079 (2017).
Gross, L., Mohn, F., Moll, N., Liljeroth, P. & Meyer, G. The chemical structure of a molecule resolved by atomic force microscopy. Science 325, 1110–1114 (2009).
Pham, V. D., Kanisawa, K. & Fölsch, S. Quantum rings engineered by atom manipulation. Phys. Rev. Lett. 123, 066801 (2019).
Gross, L. et al. High-resolution molecular orbital imaging using a p-wave STM tip. Phys. Rev. Lett. 107, 086101 (2011).
Li, Y., Zhou, Z., Shen, P. & Chen, Z. Two-dimensional polyphenylene: experimentally available porous graphene as a hydrogen purification membrane. Chem. Commun. 46, 3672–3674 (2010).
Segawa, Y., Omachi, H. & Itami, K. Theoretical studies on the structures and strain energies of cycloparaphenylenes. Org. Lett. 12, 2262–2265 (2010).
Taubert, S., Sundholm, D. & Pichierri, F. Magnetically induced currents in [n]cycloparaphenylenes, n = 6−11. J. Org. Chem. 75, 5867–5874 (2010).
Horcas, I. et al. WSXM: a software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 78, 013705 (2007).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Tersoff, J. & Hamann, D. R. Theory and application for the scanning tunneling microscope. Phys. Rev. Lett. 50, 1998–2001 (1983).
Tersoff, J. & Hamann, D. R. Theory of the scanning tunneling microscope. Phys. Rev. B 31, 805–813 (1985).
VandeVondele, J. et al. Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 167, 103–128 (2005).
Kühne, T. D. et al. CP2K: an electronic structure and molecular dynamics software package—Quickstep: efficient and accurate electronic structure calculations. J. Chem. Phys. 152, 194103 (2020).
Hartwigsen, C., Goedecker, S. & Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 58, 3641–3662 (1998).
VandeVondele, J. & Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 127, 114105 (2007).
Tang, W., Sanville, E. & Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 21, 084204 (2009).
Henkelman, G., Arnaldsson, A. & Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006).
TURBOMOLE program package for electronic structure calculations (Turbomole, 2018); https://www.turbomole.org/
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Weigend, F. & Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305 (2005).
Becke, A. D. Density‐functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Schleyer, P. V. R. et al. Nucleus-independent chemical shifts: a simple and efficient aromaticity probe. J. Am. Chem. Soc. 118, 6317–6318 (1996).
Stanger, A. Nucleus-independent chemical shifts (NICS): distance dependence and revised criteria for aromaticity and antiaromaticity. J. Org. Chem. 71, 883–893 (2006).
Gershoni-Poranne, R. & Stanger, A. The NICS-XY-Scan: identification of local and global ring currents in multi-ring systems. Chem. Eur. J. 20, 5673–5688 (2014).
Herges, R. & Geuenich, D. Delocalization of electrons in molecules. J. Phys. Chem. A 105, 3214–3220 (2001).
Jusélius, J., Sundholm, D. & Gauss, J. Calculation of current densities using gauge-including atomic orbitals. J. Chem. Phys. 121, 3952–3963 (2004).
Taubert, S., Sundholm, D. & Jusélius, J. Calculation of spin-current densities using gauge-including atomic orbitals. J. Chem. Phys. 134, 054123 (2011).
Fliegl, H., Jusélius, J. & Sundholm, D. Gauge-origin independent calculations of the anisotropy of the magnetically induced current densities. J. Phys. Chem. A 120, 5658–5664 (2016).
Ahrens, J., Geveci, B. & Law, C. in Visualization Handbook (eds Hansen, C. D. & Johnson, C. R.) 717–731 (Elsevier, 2005).
Hapala, P. et al. Mechanism of high-resolution STM/AFM imaging with functionalized tips. Phys. Rev. B 90, 085421 (2014).
Krenner, W., Kühne, D., Klappenberger, F. & Barth, J. V. Assessment of scanning tunneling spectroscopy modes inspecting electron confinement in surface-confined supramolecular networks. Sci. Rep. 3, 1454 (2013).
Acknowledgements
This work was funded by the German Research Foundation (DFG) through the Collaborative Research Center SFB 953 (project no. 182849149), the Research Unit FOR 1878, the Research Training Group GRK 1896 and AM407.
Author information
Authors and Affiliations
Contributions
A.G., K.Y.A. and S. Maier conceived the experiments and supervised the project. F.X., S.B., M.D., A.D. and S. Maier conducted the STM/STS/nc-AFM measurements and analysed the experimental data. S. Maisel performed the calculations. K.Y.A. and V.A. proposed the synthetic route to the precursors and C.R., V.A. and O.P. synthesized the precursors. S. Maier co-wrote the manuscript, with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Chemistry thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Synthesis of precursor 1.
Note that the crossed bonds in the top-right structure indicate a mixture of cis and trans isomers.
Extended Data Fig. 2 Geometry of precursors 1 & 2, tetramer and trimer.
(a-c) DFT-optimized structure of precursor 1: (a) on the gold surface, (b) planar and (c) non-planar configuration in gas phase. (d-f) DFT-optimized structure of precursor 2: (d) on the gold surface, (e) planar and (f) non-planar configuration in gas phase. The angle comprised by the connecting lines (red lines) through the two C-Br bonds in 1 (2) is 90.4° (72.0°) in the gas phase and 101.4° (78.1°) upon planarization on the Au(111). Hence, the fused pentagons bend the three phenylene units at the periphery nearly to a 90 ° target angle. Therefore, both precursors appear suitable for the effective formation of cyclic tetramers. (g-h) DFT-optimized structures of the tetramer and trimer on the Au surface. Color code: carbon (gray), bromine (orange), hydrogen (white), and gold (yellow).
Extended Data Fig. 3 Reaction products of precursors 1 and 2 on Au(111).
(a) Detailed and (b) overview STM images of precursor 1 after deposition on Au(111) kept at 570 K using a low deposition rate (~0.016 ML/min). The fully cyclized tetramers are preferably located at elbow sites in the herringbone structure, which is restored after Br desorption. (c) Detailed and (d) overview STM images of precursor 2 after deposition on Au(111) kept at 300 K and subsequent annealing to 510 K for 10 min reveal that the cleaved Br remains on the surface. Hence, the molecular structures form compact clusters surrounded by the distorted Au herringbone reconstruction. The trans coupling of both precursors resulted in chain structures, while the cis coupling led to the formation of trimers, cyclic tetramers, and cyclic pentamers. Curved chain structures occur due to additional cyclodehydrogenation reactions. Pentamer formation was observed mainly for precursor 1. The blue bonds in the chemical structure mark the C-C bonds formed after Ullmann-type coupling, while the red bonds indicate the C-C bonds formed after cyclodehydrogenation coupling. Scan parameters: (a) Scale bar: 1 nm; U = 10 mV, I = 20 pA (chain); U = 5 mV, I = 20 pA (trimer); U = −0.1 V, I = 60 pA (tetramer); U = 100 mV, I = 20 pA (pentamer). (b) Scale bar: 20 nm, U = −1 V, I = 100 pA. (c) Scale bar: 1 nm; U = −0.9 V, I = 200 pA (chain); U = −1.3 V, I = 150 pA (trimer); U = 40 mV, I = 170 pA (tetramer); (d) Scale bar: 20 nm, U = 0.3 V, I = 170 pA.
Extended Data Fig. 4 Non-contact AFM image of the fully cyclized tetramer.
(a) Experimental constant height nc-AFM image recorded with a CO-functionalized tip, and (b) corresponding calculated nc-AFM image of the tetramer. The calculated nc-AFM is based on the probe particle model described in Ref. 54. For the calculation, the DFT-optimized geometry of the fully cyclized tetramer on the Au surface (see Fig. 3b) was used (tip height above the molecule 7.65 Å and amplitude A = 100 pm). The slightly brighter contrast of the isochrysene units (corner of the macrocycle) in the measured nc-AFM image suggests that those are slightly more elevated from the Au(111) surface than the 6-membered rings formed by connecting two precursors. The contrast is also reproduced in the calculated nc-AFM image, which confirms the existence of a weak buckling in the tetramer. Scale bar: 1 nm. Nc-AFM parameters: Aosc = 100 pm, the feedback was opened at U = 5 mV, I = 20 pA with the tip placed over the molecule.
Extended Data Fig. 5 Experimental and calculated dI/dV maps of the tetramer.
Experimental dI/dV maps were taken in (a) constant current mode (CC) and (b) constant height mode (CH) at the indicated bias voltage using a CO-functionalized tip. The setpoint current was 600 pA in CC mode. The tip-molecule distance in each CH map is defined by placing the tip at the corner of the tetramer (highlighted by the red dot) at I = 600 pA and corresponding bias voltages are shown above each figure before turning off the feedback. In the CC maps, the edges of the tetramer are more pronounced due to a change in the tip-sample separation55. The map at −1.66 V has a pronounced LDOS at the tetramer’s corner, similar to the HOMO-3 in gas phase. The maps at 1.35 V, 1.20 V, and 1.03 V are presumably associated with the PIR, whereas the maps at 0.92 V, 1.15 V, and 1.6 V are associated with the NIR. The map at 2.15 V features pronounced LDOS at the tetramer’s corner, similar to LUMO + 3 in gas phase. Calculated constant height STS maps with a (c) s-wave, (d) p-wave, and (e) sp-wave tip, as well as (f) partial charge densities in the indicated energy ranges. The images shown in (b, d-e) are identical to the ones shown in Fig. 4c–e. Scale bar: 1 nm.
Extended Data Fig. 6 dI/dV line spectroscopy maps along symmetry lines of the tetramer and trimer.
dI/dV line spectroscopy maps along symmetry lines of the (a) tetramer and (b) trimer. (a) dI/dV line spectroscopy taken along the blue and green lines in the STM image on the left is shown in the two middle panels. Zoomed-in line spectra maps are shown in the right panels. The dI/dV line spectra maps feature broad localized unfilled states, while the filled states show sharp delocalized states at −1.35 V, −1.19 V, and −1.04 V (highlighted by the red arrows). There are several possible explanations for these delocalized states. Assembled circular rings can exhibit discrete electronic states that reflect generic features of quantum confinement along a closed path. In such a particle-in-a-ring system, the expected energy difference between two quantized states is \(E_n - E_m = \frac{{\hbar ^2}}{{2m_eR^2}}\left( {n^2 - m^2} \right)\) with R the radius, me the effective electron mass, and n, m the quantum number of angular momentum26. Assuming for the tetramer R = 9.825 Å (outer diameter, where ring currents are observed according to ACID plots, see Extended Data Fig. 9), we obtain E1−E0=0.04 eV, E2−E1=0.12 eV, and E3−E2=0.2 eV. This matches well with the experimentally observed energy differences of the three sharp delocalized states with E0=−1.35 eV and considering that E0 and E1 are too close in energy to be individually resolved. Therefore, these delocalized states might be associated with quantized eigenstates in a particle-in-a-ring system based on quantum confinement. The missing sharp resonances along the trimer dI/dV line spectroscopy maps corroborate this. However, these sharp peaks might also be associated with vibronic satellites with an almost constant energy spacing of 150 meV. Moreover, the experimental STS maps for these peaks match well with the calculated ones (see Fig. 4) and could be assigned to close-lying filled states. Hence, an unambiguous assignment of the three delocalized filled states is complex. (b) dI/dV line spectroscopy maps of the trimer taken along the blue, green, and red lines are shown in the right panels. The dI/dV spectra were measured with a CO-functionalized tip. Scan parameters: (a) I = 600 pA, U = 0.92 V; (b) I = 100 pA, U = −1 V; scale bar, 1 nm.
Extended Data Fig. 7 Bandgap of the trimer, tetramer, and pentamer.
dI/dV point spectra of the (a) tetramer, (b) trimer, and (c) pentamer were measured at the positions shown in the inserted STM image. The panels at the bottom show the fitted peaks (Gaussian function) to obtain the energy gap. The corresponding peaks are highlighted with red arrows in the overview dI/dV spectra. The energy gap measures 2.05 ± 0.04 eV (trimer), 1.95 ± 0.04 eV (tetramer), and 1.90 ± 0.04 eV (pentamer), respectively. Therefore, the bandgap narrows ~50 meV as the number of covalently linked precursors increases. A CO-functionalized tip was used to take the spectra on the tetramer and trimer, and a metallic tip on the pentamer. (d) Calculated energy gaps of the planar tetramer and trimer in gas phase using different codes with different functionals. The absolute energy gap of the tetramer and trimer varies within different functionals, but the energy difference between the tetramer and trimer falls in 0.181–0.199 eV, which is 121–139 meV higher than the experimental value. Note that in the VASP code plane waves are used as basis set, while for Turbomole the def2-TZVP basis set was used. Scan parameter: (a) I = 600 pA, U = 0.92 V; (b) I = 100 pA, U = −1 V; (c) I = 100 pA, U = −1.7 V. Scale bar: 1 nm.
Extended Data Fig. 8 Electronic properties of the trimer.
(a) The characteristic point dI/dV spectra of a trimer on Au(111) were acquired at the positions shown in the inserted STM image (colored dots). The frontier orbitals are pronounced at the corner of the trimer (blue dot) with an energy gap of 2.01 eV, see Extended Data Fig. 7. The observed peaks are labeled by (1)-(5). The feedback was opened at I = 100 pA, U = −1 V. (b) Calculated density of states of the trimer on Au(111). The energy range in the shaded peaks (gray) was used to simulate the STS maps. (c) Constant height dI/dV maps measured with a metallic tip at the indicated bias voltages above the maps (the feedback was turned off at I = 150 pA, U = 0.5 V). (d-e) Calculated constant height STS maps using an s-wave tip and partial charge densities corresponding to the energy ranges shown below each map. The calculated dI/dV map for (2) resembles HOMO and HOMO-1 in gas phase (see Supplementary Fig. 2), which are close in energy and have nodes (less pronounced intensity) at the ends of the trimer, while the calculated map for (1) shows combined information of HOMO-2 and HOMO-3 with a node at the trimer’s center. At positive energy, the calculated maps for (3), (4), and (5) resemble LUMO, LUMO + 1, and LUMO + 2 in gas phase, respectively. The calculated STS maps are in good agreement with the experimental ones.
Extended Data Fig. 9 Current density distribution, NICS, and anisotropy of the induced current density of uncharged and charged structures.
The current density distribution in the (a) planarized [12]CPP, (b) tetramer (planarized π-extended [12]CPP), and (c) trimer for uncharged molecules (left column) and dianions (right column). The diamagnetic component is plotted in blue, and the paramagnetic component is plotted in red. Upon charging, the diamagnetic component on the outer part of the ring is strongly enhanced for [12]CPP and the tetramer, while the trimer mainly remains unchanged. This indicates a global diamagnetic ring current for both the planarized [12]CPP and tetramer dianions. Similar behavior is observed in the NICS(1)zz calculations (d-f). Herein, negative values indicate the aromaticity in the corresponding rings, whereas positive values reflect anti-aromaticity. Again, uncharged (left column) and charged molecules (right column) are shown. For the planarized [12]CPP and the tetramer, the values are much more negative after charging, illustrating that the aromaticity of the rings is enhanced, while in the trimer, the change in the NICS values is not significant. (g-i) Anisotropy of the induced current density (ACID, isovalue: 0.002) plots with current density vectors for neutral molecules (left column) and dianions (right column). When the molecules are charged, a global diamagnetic current is induced at the outer edge of the planar [12]CPP and the tetramer, which is not observed in the trimer case.
Extended Data Fig. 10 Magnetically induced current susceptibility strengths (in nA/T).
Ring current strengths for the neutral planar [12]CPP and the π-extended planar [12]CPP, as well as their dianions and dications. The numerical integrations were carried out at the center of the bonds marked in the scheme above (a-c and 1-4). The calculations were performed at the B3-LYP/def2-TZVP level. As a reference, the current strength in benzene obtained at this level of theory is 11.8 nA/T, which agrees with previous results30,52. The dianions and dications in both cases show strong diatropic currents. This is in line with previous results for non-planar [n]CPPs (with n = 6–11) and quantifies the results obtained from the current density and ACID investigations30. For dianions, the effect is slightly larger than for dications.
Supplementary information
Supplementary Information
Supplementary computational details, synthetic details and procedures, Figs. 1–17 and references.
Source data
Fig. 1, Fig. 3, Fig. 5, Extended Data Fig. 2, Extended Data Fig. 9
DFT calculated geometry structures (.xyz format).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xiang, F., Maisel, S., Beniwal, S. et al. Planar π-extended cycloparaphenylenes featuring an all-armchair edge topology. Nat. Chem. 14, 871–876 (2022). https://doi.org/10.1038/s41557-022-00968-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41557-022-00968-3
This article is cited by
-
On-surface synthesis of enetriynes
Nature Communications (2023)
-
Orbital-symmetry effects on magnetic exchange in open-shell nanographenes
Nature Communications (2023)
-
On-surface synthesis of nitrogen-doped nanographene with an [18]annulene pore on Ag(111)
Communications Chemistry (2023)
-
On-surface synthesis of planar π-extended [12]cycloparaphenylene
Communications Chemistry (2022)