Abstract
Coulombic interactions can be used to assemble charged nanoparticles into higher-order structures, but the process requires oppositely charged partners that are similarly sized. The ability to mediate the assembly of such charged nanoparticles using structurally simple small molecules would greatly facilitate the fabrication of nanostructured materials and harnessing their applications in catalysis, sensing and photonics. Here we show that small molecules with as few as three electric charges can effectively induce attractive interactions between oppositely charged nanoparticles in water. These interactions can guide the assembly of charged nanoparticles into colloidal crystals of a quality previously only thought to result from their co-crystallization with oppositely charged nanoparticles of a similar size. Transient nanoparticle assemblies can be generated using positively charged nanoparticles and multiply charged anions that are enzymatically hydrolysed into mono- and/or dianions. Our findings demonstrate an approach for the facile fabrication, manipulation and further investigation of static and dynamic nanostructured materials in aqueous environments.

Similar content being viewed by others
Main
In one of its definitions, nanochemistry1,2 focuses on the intriguing and diverse analogies between molecular-scale and nanosized species. In a widely cited example, ligand-protected metallic nanoclusters exhibit quantized energy levels and are often referred to as ‘superatoms’3. Larger, superparamagnetic and superferromagnetic nanoparticles (NPs) behave in many ways like atoms of paramagnetic and ferromagnetic metals, respectively4,5. Various ways of encoding ‘valency’ in spherical NPs have been proposed6 and utilized to construct ‘colloidal molecules’7. NPs can also be assembled into one-dimensional (1D) structures in a process similar to the polymerization of small molecules8; indeed, the ability to visualize NPs by electron microscopy has been utilized to validate theoretical models developed for molecular polymerization. This analogy was further extended to copolymerization9 and arresting polymerization with chain stoppers10. NPs have also been assembled into 3D materials (colloidal crystals, or ‘supracrystals’) with structures that mimic those of inorganic solids11 as simple as AlB2 or NaCl, as well as ones without known atomic-scale analogues12. NP analogues of alloys and intermetallic compounds have been reported13 and very small NPs within binary assemblies were shown to behave as nanoscale electron equivalents14. Furthermore, analogies between molecular-scale and nanosized species extend to chemical reactions15. Similar to molecules, NPs can react with themselves16, be subjected to oxidation17, cation18 and anion19 exchange, and to other, more complex reactions, such as galvanic replacement20. Sequential reactions are possible21,22 and the concept of the total synthesis of inorganic nanostructures has been proposed23.
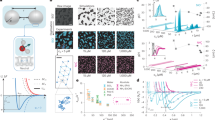
Similarly, spherical NPs functionalized with multiple charged groups (typically COO– and NMe3+) behave in many ways like nanoscale analogues of simple ions24,25. These ‘superions’ can attract each other and precipitate from solution as electroneutral solids, analogously to simple inorganic salts, such as AgI. There are, however, some notable differences between the behaviour of small ions and charged nanoscale species. Figure 1a (left) shows an illustrative titration curve for the titration of Ag+ with I–, whereby precipitation occurs abruptly when the solubility product, Ksp = [A+][B–], is reached. In contrast, the titration of positively charged NPs with negatively charged ones leads to a gradual increase in the NP aggregate size26 until precipitation occurs at a point of electroneutrality (that is, the number of positively charged ligands on the added NPs reaches the number of negatively charged ligands on the titrated ones). Further addition of the negatively charged NPs leads to dissolution of the precipitate and the formation of increasingly smaller NP aggregates (Fig. 1a, right), which is not observed for small, non-complexing anions.
a, Typical aggregation behaviour of oppositely charged species on a molecular scale (ions; left) and a nanoscale (“superions”; right). b, Structural formula of TMA ligand used to stabilize gold NPs in water (counterion, Br–); right: a representative TEM image of TMA-functionalized 7.4 nm Au NPs (Au·TMA). c, Examples of multiply charged anions capable of mediating attractive interactions between Au·TMA. d, Schematic (left) and representative titration curve (right) for the titration of Au·TMA (here, 11.4 nm; overall, 20 nmol TMA groups) with EDTA trisodium salt. The dashed red line denotes the point of electroneutrality (~6.7 nmol trianionic EDTA3–). e, Schematic (left) and representative titration curve (right) for the titration of EDTA (trisodium salt) (6 nmol) with 11.4 nm Au·TMA. The dashed red line denotes the point of electroneutrality (18 nmol TMA on Au NPs).
Interactions between oppositely charged small ions (for example, Ag+ and I–) and, more recently, between oppositely charged nanosized species24,25,27,28,29 have been investigated extensively. In contrast, relatively little attention has been devoted to studying electrostatic interactions across length scales, that is, between charged NPs and small molecules that bear opposite charges. Here we investigated the ability of small-molecule ions to mediate attractive interactions between oppositely charged NPs. Importantly, we found that a sharp transition between non-mediators and mediators occurs between doubly and triply charged molecules. Taking advantage of this finding, we prepared a family of colloidal crystals and developed a dissipative self-assembly (DSA) system whereby NPs exist in the assembled state only during the continuous application of an oligoanion stimulus.
Results and discussion
Interactions between positively charged nanoparticles and small anions
A fundamental question to address when considering interactions between oppositely charged NPs and molecules is: what is the minimum number of charges on a small molecule required to induce attractive interactions with—and consequently, mediate the self-assembly of—oppositely charged NPs in water? To this end, we synthesized differently sized spherical gold NPs functionalized with ligand ((11-mercaptoundecyl)-N,N,N-trimethylammonium (TMA); Fig. 1b) terminated with the positively charged ammonium groups and studied their interactions with simple anions that comprised increasing numbers of negative charges. Irrespective of the diameter of the metallic core (we worked with NPs of various sizes between 2.8 and 13.1 nm), the particles exhibited an excellent solubility in water (with Br– as the counterion; Fig. 1b, right), as reported previously24,30. The colloidal stability of these NPs was not affected by the addition of aqueous solutions of various doubly charged anions (we tested carbonate (CO32–), sulfate(VI) (SO42–), hydrogen phosphate(V) (HPO42–), chromate(VI) (CrO42–), tartrate and oxalate, all at pH values greater than pKa2, to ensure double deprotonation), even when used in a 100-fold excess with respect to NP-bound TMA groups. In sharp contrast, all triply charged anions tested, which included citrate, trimetaphosphate and triply deprotonated ethylenediaminetetraacetic acid (EDTA3–), caused a redshift of the NPs’ surface plasmon resonance (SPR) band, indicative of NP aggregation. Aggregation was also induced by anions that featured greater numbers of negative charges, which included fully deprotonated EDTA (EDTA4–), pyrophosphate (P2O74–), triphosphate (P3O105–) and hexametaphosphate ((PO3)66–) (see Supplementary Fig. 4 for structural formulas). In all cases, aggregation was confirmed by transmission electron microscopy (TEM), which showed the formation of mostly amorphous NP aggregates (Supplementary Fig. 6).
To better understand these results, we performed molecular simulations of TMA-coated NPs interacting with HPO42– and citrate as model doubly and triply charged anions, respectively (for details, see Supplementary Section 4). First, we studied the interactions between a positively charged NP surface and individual anions by all-atom (AA) molecular dynamics (MD) simulations (Fig. 2a,b). To this end, we simulated a NP hemisphere (d = 7.4 nm) decorated with 347 TMA ligands (with Cl– as the counterions) in the presence of citrate3–, HPO42– or an extra Cl– ion (neutralized with three, two or one Na+ counterions, respectively). We investigated the interactions between the positively charged NP surface and individual anions by AA metadynamics simulations31,32,33 (Fig. 2a,b). During these simulations, the anions bound to and unbound from the NP surface multiple times (Fig. 2a), which allowed us to retrieve the free-energy profiles for their interaction with the NP (Fig. 2b). The minima at d ≈ 5 Å are indicative of the attractive interactions of all three anions with the NP-bound ligands, with the depth of the minimum proportional to the interaction free energy. We found that the difference in the interaction energy was proportional to the ionic valence, within the precision of the AA metadynamics technique (ΔG, ~2.7 kcal mol–1 for Cl–, ~3.9 kcal mol–1 for HPO42– and ~6.1 kcal mol–1 for citrate3–).
a, Atomistic model of one-half of a TMA-functionalized Au NP (here interacting with citrate) used in the AA simulations. b, Free-energy profile for the interaction between Au·TMA and Cl– (yellow), HPO42– (blue) or citrate3– (red) (expressed as a function of the distance d between the centre of mass of the anion and the centre of mass of the closest TMA charged headgroup; errors bars are the s.e.m.). c, Snapshots from CG-MD simulations of two TMA-coated Au NPs in the presence of HPO42– (top) or citrate3– (bottom). d, Distance between the centres of two TMA-functionalized Au NPs in the presence of HPO42– (blue) or citrate3– (red) as a function of the CG-MD simulation time.
Next, we studied the ability of HPO42– and citrate to mediate attractive interactions between two TMA-coated Au NPs (Supplementary Section 4.1). In these AA metadynamics simulations, 10 citrate3– or 15 HPO42– (neutralized by 30 Na+) were placed between two NP halves, each decorated with 347 TMA groups (with the same number of Cl– ions). Throughout these simulations, the distance between the NPs was varied repeatedly, which allowed us to estimate the free energy of the NP–NP interaction as a function of NP–NP separation (Supplementary Fig. 9). With citrate, the free-energy profile extracted from the AA metadynamics simulation exhibited a minimum at the NP centre-to-centre distance of ~9.4 nm, which indicates that the NPs have a tendency to assemble. However, on replacing citrate with HPO42–, this energy minimum disappeared and the global energy minimum moved towards larger distances (>10.5 nm), which corresponds to the disassembled state (Supplementary Fig. 9b).
To model the anion-mediated self-assembly of positively charged NPs on a larger scale, we utilized coarse-grained molecular dynamics (CG-MD) simulations (Supplementary Section 4.2). Figure 2c shows snapshots from CG-MD simulations of two TMA-coated Au NPs, each decorated with 804 TMA residues, neutralized by the corresponding number of HPO42– or citrate3– anions (804 and 536, respectively). Whereas both anions exhibited a strong affinity to the NPs, only citrates had the ability to bring the particles together during the CG-MD runs. This conclusion is also evident from Fig. 2d, in which we plotted the distance between the centres of masses of the two NPs as a function of the CG simulation time.
To gain further insight into the NP aggregation behaviour, we titrated suspensions of TMA-coated Au NPs (that is, Au·TMA) in water with an aqueous solution of another trianion, namely, triply deprotonated EDTA (Fig. 1c) and followed the change in the position of Au NPs’ SPR band, λSPR. Initially, λSPR corresponded to ~520 nm, typical of non-interacting NPs; a redshift of the SPR band is indicative of NP aggregation. We found that on the addition of EDTA3–, λSPR redshifts following a sigmoidal curve, and then stabilizes on the addition of ~0.5 equiv. EDTA3– with respect to the TMA groups (Fig. 1d), which corresponds to ~150% of the amount expected to achieve the electroneutrality point. No further changes were observed with higher amounts of the titrant (Fig. 1d). This aggregation profile is akin to that of the precipitation of a water-insoluble inorganic salt (Fig. 1a, left).
Our results are consistent with the Schulze–Hardy rule34,35, which states that the ability of an electrolyte to mediate interactions between—and induce coagulation of—charged colloids is proportional to the electrolyte’s ionic valence, z. Specifically, the critical coagulation concentration (CCC) scales with z as CCC ∝ z–6, which indicates that a small increase in charge can greatly increase the ion’s potency to trigger coagulation36. For example, an increase in the charge from –2 (for HPO42–) to –3 (for citrate3–) decreases the CCC value by as much as ~11-fold. In other words, the assembly of Au·TMA would require a much higher concentration of HPO42– than of citrate3–. However, at this high concentration, the ionic strength of the solution is high enough to screen the electrostatic interactions; hence, the assembly of Au·TMA using divalent (or monovalent) anions is not observed.
The Schulze–Hardy rule states that CCC is sensitive to the number of charges on the electrolyte, but not to the way these charges are distributed across the anion. However, we hypothesized that flexible anions might be more potent in mediating the self-assembly of TMA-coated Au NPs, by interacting with NP-bound TMA groups more efficiently. To address this question, we titrated 5.2 nm Au·TMA with three different tricarboxylates, which differed only in the number of methylene groups: propane-1,2,3-tricarboxylate, butane-1,2,4-tricarboxylate and pentane-1,3,5-tricarboxylate (Supplementary Section 5). These experiments showed no appreciable difference in the behaviour of the titrant (Supplementary Fig. 15). We also worked with the substantially more rigid benzene-1,3,5-tricarboxylate, only to find that the titration profile remained the same. Based on these results, we conclude that the conformational flexibility of oligoanions has little effect on their propensity to mediate the assembly of positively charged NPs, at least in this series.
To further demonstrate the importance of Coulombic interactions in our system, we prepared aqueous suspensions of differently sized Au·TMA (4.8, 8.8 and 13.1 nm) and titrated them with the same solution of EDTA3– (Extended Data Fig. 1). If the contribution of van der Waals interactions to the formation of NP aggregates is substantial, the largest NPs would aggregate first, followed by the 8.8 and 4.8 nm NPs. We found, however, that the aggregation profiles for all three NP sizes were practically the same, which indicates that the interparticle interactions in our system are governed predominantly by electrostatics.
Remarkably, reversing the order of titration resulted in a drastically different NP aggregation behaviour. When a solution of EDTA3– in water was titrated with aqueous Au·TMA, the added NPs assembled into increasingly large aggregates, which subsequently decreased in size on the continued addition of the NPs, and eventually resulted in a suspension of non-interacting NPs (Fig. 1e). This aggregation/disaggregation profile is reminiscent of that previously observed for mixtures of positively and negatively charged NPs (Fig. 1a, right). Interestingly, however, the highest degree of aggregation was consistently observed after the addition of only one-third of the NPs required to achieve electroneutrality (denoted by a dashed red line in Fig. 1e; note the position of the maximum with respect to the line). Overall, our results indicate that (1) the yield of electroneutral aggregates that comprise ‘superions’ and small-molecule counterions is maximized in the presence of an excess of the latter, which can be attributed to the entropic penalty associated with bringing multiple small ions together, and (2) once formed, these electroneutral aggregates can be disassembled with an excess of ‘superions’, but not molecular-scale ions, and thus combine the characteristics of a molecular-scale system (ionic aggregates; Fig. 1a, left) and a nanoscale system (aggregates of oppositely charged NPs; Fig. 1a, right).
Dynamics of small ions within nanoparticle–molecule ionic aggregates and their structural transformation into crystalline assemblies
The CG-MD simulation described above demonstrates that citrate ions can readily mediate attractive interactions between two positively charged TMA-coated NPs (Fig. 2c). Next, we investigated the mobility of citrates within the resulting ensemble of two bound Au·TMA NPs. To this end, we extended the CG-MD simulation and analysed the trajectory that covered the period from 0.9 μs (that is, once the NPs had stably aggregated; Fig. 2c,d) to 8.4 μs. We turned to machine learning to study the variability of the arrangement of citrates in the system. We used an unsupervised clustering method—specifically, the Probabilistic Analysis of Molecular Motifs37—employing the Smooth Overlap of Atomic Positions38 as rich descriptors of the molecular environment that surrounded each citrate in the molecular model. Such an analysis allows the classification of different citrates based on differences in the local environment that surrounds them during the CG-MD (namely, pertaining to local order, persistency in the interactions and so on) to follow the local variations and fluctuations in the citrate states and also to reconstruct the dynamic mobility of the citrates in different regions of the system39. The analysis subdivides the citrates in the system into three distinct clusters (states): (1) citrates located at the interface between the two NPs (red in Fig. 3a), (2) citrates that interact with a single NP (grey) and (3) an intermediate state between the first two (green) (for details, see Supplementary Section 4.2.2). The movement and reshuffling of citrates between the three clusters during the CG-MD reveal the dynamics between the states (Fig. 3a, left versus right).
a, Snapshots from a CG-MD simulation of two Au·TMA NPs in the presence of citrate ions after stable binding of the two NPs (0.9 µs), and at the end of the CG-MD simulation (8.4 µs). Red, green and grey identify citrates grouped into three different clusters (see text) at t = 0.9 µs (the NPs are represented as solid yellow spheres, with the TMA ligands omitted for clarity). b, A 2D FES associated with the configurations of citrate ions as a function of two variables, CONT and DIST (for definitions, see Supplementary Section 4.2.2). The areas encircled by dashed-line ovals denote three local energy minima that correspond to citrates interacting with a single NP (grey), located at the interface between the two NPs (red) and an intermediate state (green). The black arrows denote transitions between the three states, and the numbers next to the arrows indicate the relative probability of a given transition. c, Annealing of Au·TMA/citrate aggregates at 23 °C over 24 h. d, Annealing of Au·TMA/citrate aggregates at 50 °C over 24 h. e, Representative cryo-STEM bright-field image of an Au·TMA/P3O105– aggregate. The entity inside the turquoise square is a NP55 Mackay cluster. f, Top: voxel projections of the tomographic reconstruction of the cluster marked in e. The three projections shown correspond to the fivefold (left), threefold (centre) and twofold (right) symmetry. Bottom: matching projections of a model Mackay cluster. Inset scale bars, 50 nm. a.u., arbitrary units.
From the CG-MD trajectory, we also constructed a 2D free-energy surface (FES) of the citrates in the system (Fig. 3b), represented as a function of two variables (the contact variable, CONT, which describes the number of contacts with NP-adsorbed TMA ligands, and the distance variable, DIST, which describes the position of a citrate on the NP cluster; Supplementary Fig. 13). This analysis identified three local free-energy minima in the FES (Fig. 3b), consistent with the unsupervised clustering classification obtained above.
By tracking the individual citrates during the CG-MD simulation, we could monitor their transition probabilities between the three states. Such probabilities, obtained by computing the transition matrix among the three different states from the clustering analysis of the CG-MD (Supplementary Fig. 12d), are reported next to the arrows inside the FES in Fig. 3b. These transition probabilities are extracted from a simplified CG model, and thus have a qualitative value; nonetheless, they can be compared to one another and are proportional to the rate constants of citrates in one state transitioning to another. Moreover, we computed the mean square displacement of citrates in different clusters (Supplementary Fig. 14), which, even accounting for simplifications in the model, allowed us to estimate the diffusion of the ‘grey’ citrates across the NP surface as being about one order of magnitude faster than that of the more static ‘red’ citrates. Thus, these results demonstrate the internal dynamics of the system, in which the citrates at the interface between two bound NPs are less dynamic (but not completely static) than those bound to the surface of a single NP.
We hypothesized that the facile diffusion of oligoanions between positively charged NPs, as revealed by the MD simulations, might facilitate the transformation of the initial, mostly amorphous, aggregates into regular, crystalline assemblies (which represent the thermodynamic minimum of the system). Indeed, we found that when left undisturbed in an aqueous suspension at room temperature, the Au·TMA/citrate precipitates developed multiple crystalline domains over the course of 24 hours (Fig. 3c, bottom). At an elevated temperature (50 °C), the ‘annealing’ process was complete within one hour and resulted in colloidal crystals 200–300 nm across, which did not grow further (Fig. 3d). Overall, the observed increase in the NP order within the Au·TMA/citrate aggregates supports the idea of the oligoanions acting as a dynamic—as opposed to ‘frozen’—ionic glue.
To characterize the crystalline assemblies, we utilized cryogenic TEM (cryo-TEM)—a technique that preserves the native (solution) structures during imaging. However, cryo-TEM requires that the specimens be very thin—we thus attempted to image aggregates obtained immediately after treating the TMA-coated Au NPs with an oligoanion (here P3O105–). Interestingly, whereas these aggregates appeared amorphous at a low magnification (Fig. 3e), close inspection revealed that they were composed of small (~20–50 nm) interconnected aggregates that featured a regular arrangement of NPs; thus, they exhibited a short-range crystalline order. In particular, we observed multiple instances of ~25 nm aggregates that we identified by cryo-scanning transmission electron microscopy (cryo-STEM) tomography as Mackay icosahedra40 (Fig. 3f). Within these aggregates, the central NP was surrounded by a 12-NP icosahedral shell, which was enclosed inside an outer, deltahedral shell composed of 42 NPs, and so gave rise to a closed-shell, ‘magic number’ cluster that consisted of 55 NPs. The formation of clusters that maximize the packing density of like-charged NPs may seem surprising, but is enabled by the presence of small, oppositely charged molecules that compensate for the electric charges on the NPs. Based on our tomography results, we determined the nearest-neighbour distance within the Mackay icosahedron (Fig. 3f) as 8.1 nm. Given that the aggregate was composed of 4.73 nm NPs, the gap between the metallic cores was equal to 3.37 nm—slightly more than twice the length of a TMA ligand in its fully extended conformation (2 × 1.64 nm, which is the distance between the surface of Au and the terminal N atom), which leaves enough space for a monolayer of P3O105– anions.
Crystalline aggregates of oppositely charged nanoparticles and small ions
We hypothesized that the attractive electrostatic interactions between positively charged NPs and oligoanions could be used to construct large colloidal crystals (‘supracrystals’), and ultimately nanostructured materials. As the annealing experiments shown in Fig. 3c,d did not afford crystalline domains larger than ~300 nm, we sought another method to prepare crystalline assemblies of our NPs. A previously reported method to generate ordered assemblies of ionic NPs is based on (1) generating amorphous aggregates by electrostatic interactions between oppositely charged nanosized entities, (2) adding an inorganic salt (typically NaCl) at a high concentration to screen the electrostatic interactions and therefore to disassemble the initial aggregates41,42, and (3) slowly decreasing the ionic strength of the solution by dialysis against pure water. Although this strategy has been successfully applied to generate ordered assemblies of positively charged NPs and negatively charged DNA43, it is not applicable to our system, in which small-molecule anions would diffuse through the dialysis membrane and leave the solution, along with the screening agent. However, we hypothesized that this problem could be tackled by employing an intrinsically unstable screening agent that (1) bears no more than two negative charges on the anion (to avoid mediating the NP assembly) and (2) undergoes a spontaneous decomposition into non-ionic products, thus slowly reducing the ionic strength of the solution and triggering electrostatic interactions in the system. These criteria are met by ammonium carbonate, whose added benefit is that the decomposition products (NH3 and CO2) are gaseous and spontaneously leave the system44:
We were pleased to find that (1) the addition of ammonium carbonate induced the redissolution of all the ion/superion precipitates described above (we worked with a concentrated (NH4)2CO3 solution, c ≈ 2.5 M), and (2) the spontaneous decomposition of (NH4)2CO3 resulted in the formation of well-defined colloidal crystals (over the course of about 24 hours) (Fig. 4a).
a, Schematic illustration of the method for anion-mediated crystallization of Au·TMA (the counterion for multiply charged anions, indicated in green, is Na+). Ammonium ions and ammonia are shown in red; carbonate ions and carbon dioxide are shown in blue). b–h, Representative SEM images of colloidal crystals of Au·TMA and various multiply charged anions: P3O105– (b,e,g,h), EDTA3– (f), citrate3– (d) and ATP4– (c). The size of the Au NPs was 7.4 nm (b,c,e), 11.4 nm (d,f) and 4.7 nm (g,h). For additional images, see Extended Data Fig. 1. i, Optical micrograph of colloidal crystals of 4.7 nm Au·TMA and P3O105–. j, 1D X-ray diffraction (SAXS) patterns for 4.73 nm Au·TMA/P3O105– crystals. SAXS data are plots of scattered intensity I(q) versus the scattering vector q. Black traces are experimental data; pink and blue traces are the modelled SAXS patterns for perfect lattices (pink, a = 121.3 Å; blue, a = 130.9 Å). k, Proposed models of binding within crystals with a smaller (top, major species) and larger (bottom, minor species) lattice constants. l, 1D SAXS patterns for 4.73 nm Au·TMA/ATP crystals. Black traces are experimental data; pink and blue traces are modelled SAXS patterns for perfect lattices (pink, a = 119.8 Å; blue, a = 130.9 Å).
Figure 4b–h shows representative scanning electron microscopy (SEM) images of colloidal crystals that comprise TMA-coated Au NPs and various multiply charged anions (for additional examples, see Extended Data Fig. 2 and Supplementary Section 6). Interestingly, the crystallinity of the assemblies was not compromised by the presence of relatively large uncharged moieties on the anions—for example, replacing triphosphate P3O105– with ATP resulted in crystals of the same quality (Supplementary Fig. 18). Irrespective of the anion and the NP size, the NPs assembled into close-packed colloidal crystals whose average sizes could be controlled in the 1–50 μm range simply by tuning the concentration of NPs during crystallization between 0.16 and 10 mg ml–1 (Supplementary Figs. 17 and 18). The largest crystals were obtained from 4.7 nm Au·TMA as thin hexagonal plates with an edge-to-edge distance of >50 μm, which corresponds to as many as ~6,000 NPs arranged regularly in a row; these crystals were sufficiently large to be imaged by optical microscopy (Fig. 4i). In terms of the number of repeating unit cells (>4,000), they represent some of the highest-quality colloidal crystals from small NPs obtained to date. We believe that this long-range order is enabled by the mobility of the mediating oligoanions between the TMA-coated NPs (as revealed by the MD simulations). This mobility (particularly pronounced at the early stages of aggregation, when the ionic strength is still relatively high) can enable the NPs to adjust their positions and optimize the packing within the aggregate, which ultimately results in a long-range crystalline order.
Analysis of the SEM images revealed that irrespective of the oligoanion used, the colloidal crystals exhibited morphologies (habits) typical of atomic crystals with a face-centred cubic (fcc) lattice45, including hexagonal plates (Fig. 4c) and truncated decahedra (Fig. 4e). Moreover, we directly observed the lowest-energy crystal facets of fcc lattices, namely, (111) and (100) (Extended Data Fig. 3). To confirm the fcc structure, we analysed colloidal crystals assembled from 4.73 nm Au·TMA and P3O105– by synchrotron-based small-angle X-ray scattering (SAXS). Figure 4j shows a 1D SAXS pattern of an aqueous suspension of the colloidal crystals. Interestingly, repeated measurements on several samples of Au·TMA/P3O105– crystals consistently revealed the presence of two types of fcc lattices (major and minor). The pink trace is a simulated pattern for a fcc crystal with a lattice constant, a = 121.3 Å, that corresponds to the dominant structure. This value of a corresponds to the NP centre-to-centre distance of 8.58 nm; given the diameter of the metallic core is 4.73 nm and twice the TMA monolayer thickness (~1.64 nm, defined as the distance between the NP surface and the terminal N atom) is about 3.28 nm, the gap between the fully extended TMA ligands on the neighbouring NPs is 0.57 nm. We note that this value is slightly larger than those within Mackay icosahedra (which were obtained from P3O105– and the same batch of NPs); this small increase can be attributed to the larger interparticle distance within an fcc lattice compared with that in a densely packed icosahedral cluster.
For the minor fcc species simulated by the blue trace in Fig. 4j, we found that a = 130.9 Å. The two lattices coexisted throughout the aqueous suspension, although the relative intensities of their signals depended on the location within the sample. Interestingly, these results could be correlated with SEM imaging, which often showed a bimodal size distribution of the colloidal crystals. For example, Supplementary Fig. 19 shows a mixture of ~5 and ~20 μm crystals obtained after the slow removal of (NH4)2CO3 from a solution of 4.73 nm Au·TMA and P3O105–. We hypothesize that the small crystals might correspond to the minor (that is, large-a) lattice found by SAXS, and the larger ones to the major (small-a) one. We note that at the onset of crystallization, the solution contained a substantial amount of CO32– and NH4+. Whereas the former ions are incapable of mediating attractive interactions between the NPs, the latter can readily interact with P3O105– adsorbed onto the TMA-coated NPs by means of both electrostatic and hydrogen-bonding interactions, which can result in the entrapment of NH4+ within the crystals, as schematically illustrated in Fig. 4k, bottom (indeed, the gap between the extended TMA ligands in this large-a lattice is about 1.25 nm, that is, it is slightly more than twice the gap in the small-a lattice). Over time, however, the amount of NH4+ in the system decreases, and the growth of these crystals is arrested at the expense of the small-a crystals illustrated in Fig. 4k, top.
We also investigated colloidal crystals composed of the same 4.73 nm NPs and ATP and similarly found the coexistence of a major species with a smaller a (119.8 Å) and a minor species with a larger a (130.9 Å) (Fig. 4l). The lattice constant for the major species corresponds to the interparticle gap (the distance between the terminal N atoms of the fully extended TMAs) of ~0.46 nm. The smaller gap found in the Au·TMA/ATP crystals (compared with ~0.57 nm for Au·TMA/P3O105–) may seem surprising, given the substantially larger size of ATP compared with that of P3O105– (which is essentially ATP that lacks the nucleoside moiety). However, it is reasonable to hypothesize that the organic part of ATP might intercalate between the alkane chains of the NP-adsorbed TMA ligands, and thus strengthen the interactions within the Au·TMA/ATP aggregates.
Interactions between negatively charged nanoparticles and small cations
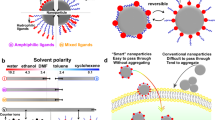
Next, we were interested in determining whether the observed behaviour can be extended to a ‘reverse’ system of negatively charged NPs and oligocations. To address this question, we synthesized (1) 4.7 nm Au NPs coated with thiols terminated with sulfonate groups (11-mercaptoundecanesulfonate (MUS) in Fig. 5a; note that we used sulfonate rather than carboxylate end groups to ensure a maximum degree of deprotonation46) and (2) small molecules that bore three and two positively charged quaternary ammonium groups (octamethyldiethylenetriammonium (OMA3+) and hexamethylethylenediammonium (HMA2+) in Fig. 5b). On the dropwise addition of an aqueous solution of OMA3+ to MUS-coated Au NPs (that is, Au·MUS) in water, an S-shaped titration curve was observed (Fig. 5c), similar to the titration profile of Au·TMA with oligoanions. However, we consistently observed that a slight excess of OMA3+ (with respect to the amount of oligoanions used to titrate Au·TMA) had to be added to reach the curve’s inflection point (denoted by the dashed red line in Fig. 5c; compare with Fig. 1d for EDTA3–). As expected, the control dication HMA2+ did not mediate interactions between Au·MUS (Fig. 5c), even when used in a large excess (Supplementary Fig. 21).
a, Structural formula of MUS used to stabilize gold NPs in water (counterion, Na+) (left) and a representative TEM image of MUS-functionalized 4.7 nm Au NPs (right). b, Structural formulas of an organic trication capable of mediating attractive interactions between Au·MUS (OMA3+) and a control dication (HMA2+) (counterions, I–). c, Representative titration curve (filled circles) for the titration of Au·MUS (4.7 nm; overall 50 nmol MUS groups) with OMA3+. The dashed red line denotes the point of electroneutrality (~16.7 nmol OMA3+). Control titration (open circles) with HMA2+. d, Representative titration curve (filled circles) for the titration of OMA3+ (20 nmol) with 4.7 nm Au·MUS. The dashed red line denotes the point of electroneutrality (60 nmol MUS on Au NPs). Control titration (open circles) of HMA2+ with the same NPs. e,f, Representative SEM images of colloidal crystals of Au·MUS and OMA3+.
Similarly, titrating a solution of OMA3+ with Au·MUS afforded NP aggregates, which gradually disassembled as more Au·MUS was added (Fig. 5d). The analogy to the original Au·TMA/oligoanions system could be extended further: on increasing the ionic strength using (NH4)2CO3, the Au·MUS/OMA3+ aggregates dissolved as the electrostatic interactions were screened; moreover, the slow decomposition of (NH4)2CO3 that followed resulted in the formation of well-defined colloidal crystals (Fig. 5e,f and Extended Data Fig. 4).
Out-of-equilibrium aggregates of oppositely charged nanoparticles and oppositely charged small ions
The above results indicate that small anions that bear three (or more) negative charges can mediate attractive interactions between positively charged NPs, which remain unassembled in the presence of mono- or dianions. These findings led us to hypothesize that a spontaneous decrease in the charge of the ‘anionic glue’ within the aggregates of Au·TMA should entail the disassembly of these aggregates. Such a charge reduction could occur as a result of the hydrolysis of multiply charged anions, which, owing to their high charge density, are often thermodynamically unstable and can be catalytically decomposed into smaller, mono- and dianionic species. A prime example of such a process is ATP hydrolysis—a highly exergonic reaction catalysed by phosphatase enzymes47. Therefore, we reasoned that in the presence of a phosphatase, ATP would act as a stimulus for the transient generation of NP aggregates (Fig. 6a).
a, Structural formulas of ATP and inorganic triphosphate. b, Schematic representation of the ATP-induced DSA of Au·TMA. The assembly/disassembly cycle is coupled to an exergonic reaction of the hydrolysis of ATP into AMP and HPO42–. c, A series of ultraviolet–visible absorption spectra of TMA-functionalized 7.4 nm Au NPs (nTMA = 19.2 nmol) in the presence of 11.1 units of apyrase per mL before and after injecting a solution of ATP (nATP = 54 nmol). d, Changes in the maxima of the dynamic light scattering profiles of a solution of the same Au·TMA (with 11.1 units of apyrase per mL) after injecting 40.5 nmol ATP at t = 0. e, Representative SEM images of 7.4 nm Au·TMA (11.1 units of apyrase per mL) before (t = 0) and after different time intervals following the injection of 54 nmol ATP. f, Six cycles of DSA of Au·TMA in the presence of 1,000 units of ALPase per mL, followed by monitoring the position of the NPs’ SPR band. For each cycle, 54 nmol ATP was used. g, Six cycles of DSA of Au·TMA (1,000 units of ALPase per mL), followed by monitoring the absorbance at 800 nm. Each cycle was initiated by injecting 54 nmol ATP. h, Stimulus-dependent disassembly profiles of aggregates of Au·TMA in the presence of ALPase (200 units of ALPase per mL). Filled triangles, ATP (12 nmol); open circles, inorganic triphosphate (9 nmol). i, Representative cryo-TEM image of 4.7 nm Au·TMA/P3O105– aggregates. j, Representative cryo-TEM image of 4.7 nm Au·TMA/ATP aggregates. Inset scale bar, 20 nm. k, Controlling the lifetimes of dynamic NP aggregates by the amount of ATP injected at t = 0 (in all cases, 200 units of ALPase per mL were used). l, Controlling the lifetimes of dynamic NP aggregates by the amount of a phosphatase enzyme (here apyrase; in all cases, 54 nmol ATP were injected at t = 0). In b–d,h, the syringe indicates the injection of an oligophosphate stimulus and the petrol pump indicates the availability of the stimulus.
The blue trace in Fig. 6c (labelled ‘start’) shows an ultraviolet–visible absorption spectrum of an aqueous solution of TMA-functionalized 7.4 nm Au NPs in the presence of a phosphatase enzyme, potato apyrase. The λSPR value of the solution is centred at 519 nm, which indicates that the particles are well dispersed in the solution. On injection of an ATP aliquot, λSPR rapidly increased and stabilized (within two minutes) at ~565 nm, accompanied by a pronounced increase in absorbance at 800 nm (A800)—that is, changes indicative of NP aggregation. We were pleased to find that at t ≈ 60 minutes, A800 started to decrease sharply and the initial spectrum was regenerated within the next 20 minutes, which shows that the process is reversible. A similar assembly/disassembly profile was observed by dynamic light scattering, in which the addition of ATP resulted in the rapid formation of ~90 nm aggregates, which persisted for ~100 minutes, and then disassembled within a relatively short period of time (Fig. 6d). SEM imaging revealed the amorphous nature and lack of long-range order within these aggregates (Fig. 6e, Supplementary Figs. 23 and 24 and the TEM images in Supplementary Fig. 25).
The equilibrium state of our system corresponds to ATP hydrolysed into AMP and HPO42–, neither of which induces the self-assembly of Au·TMA. However, as the ATP-induced self-assembly of NPs is faster than ATP hydrolysis, NP aggregates will exist temporarily—in the out-of-equilibrium regime—for as long as ATP is present at a sufficiently high concentration. Therefore, an assembly/disassembly cycle is associated with a chemical reaction that involves the consumption of a high-energy species (‘energy dissipation’), which constitutes an example of DSA48,49,50,51,52. The DSA of NPs has been reported for silicon53, gold54 and polystyrene55 particles; however, in all cases the self-assembly was triggered by small-molecule ‘fuels’ that are not biocompatible.
To verify that the disassembly of NP aggregates was triggered by the enzymatic activity of apyrase, we worked with a non-hydrolysable ATP analogue, adenosine [β,γ-imido]-triphosphate56 (Supplementary Fig. 4). We found that whereas this oligoanion induced NP aggregation similarly to ATP, the aggregates that resulted showed no signs of the disassembly in the presence of the enzyme. Similarly, aggregates obtained from Au·TMA and other multiply charged anions—such as pyrophosphate and triphosphate—remained static in the presence of apyrase. At the same time, pyrophosphate and triphosphate can be hydrolysed by another enzyme from the phosphatase family, namely, alkaline phosphatase (ALPase), which is not specific for ATP. Indeed, the addition of either P2O74– or P3O105– to an aqueous solution of Au·TMA in the presence of ALPase resulted in assembly followed by disassembly (Supplementary Fig. 35)—the latter not observed with apyrase.
Once the oligophosphate stimulus was consumed and the system returned to its non-assembled, equilibrium state, a new assembly/disassembly cycle could be initiated by injecting a fresh aliquot of the stimulus (Fig. 6f). Remarkably, the optical properties and structure of the aggregates generated in the sixth cycle were indistinguishable from those obtained by the initial injection of ATP (Fig. 6f,g), although it took them about three times as long to disassemble completely (Fig. 6f; also see Supplementary Fig. 26). Differently sized NPs behaved similarly (Supplementary Figs. 27–29). More than 20 assembly/disassembly cycles could be performed with TMA-functionalized Au NPs using various multiply charged oligophosphates. This high recyclability stands in sharp contrast to many other synthetic DSA systems, in which only up to several cycles are typically observed57,58,59. In these previously reported systems, the chemical ‘waste’ generated during the initial cycles often interferes with the subsequent assembly processes. We attribute the comparatively excellent performance of our system to the non-invasive nature of the waste—AMP and HPO42–—which, as dianions, are incapable of inducing NP aggregation. However, owing to the slightly weaker basicity of the ‘waste’ anions, compared with that of the ATP stimulus, the solution pH drops when the number of assembly/disassembly cycles increases, which lowers the enzyme activity and therefore extends the lifetimes of the transient aggregates. Furthermore, repeated cycling results in a gradual increase in the ionic strength of the solution, which ultimately prevents NP aggregation owing to the screening of electrostatic interactions between Au·TMA and the oligoanions.
Remarkably, we observed very different disassembly profiles for the aggregates of Au·TMA in the presence of ALPase, depending on the anion used (Fig. 6h). The addition of both ATP and inorganic triphosphate resulted in rapid aggregation of the NPs (Fig. 6h, t = 0–3 min). However, whereas Au·TMA/ATP aggregates persisted for a defined period of time, after which they rapidly disassembled, the disintegration of the aggregates obtained from P3O105– began soon after they formed, and proceeded at a steady rate until a solution of free NPs was regenerated after several hours (Fig. 6h, the filled triangles and open circles, respectively). To better understand these results, we prepared both types of aggregates (Au·TMA/ATP and Au·TMA/P3O105–) in the absence of the enzyme and compared their structures using cryo-TEM (to avoid artefacts resulting from sample drying). As mentioned above, Au·TMA/P3O105– was composed of small, pseudospherical ~20–50 nm NP aggregates linked into larger, branched structures (Fig. 6i; also see Supplementary Fig. 39). The formation of such ‘aggregates of aggregates’60,61,62,63 is not surprising, given that the mediating agent (P3O105–) was used in the amount necessary to compensate for the overall positive charge on the NPs. Surprisingly, however, analogous primary aggregates obtained using ATP persisted without aggregating further (Fig. 6j; also see Supplementary Fig. 40). We also analysed both types of aggregates in more detail by cryo-STEM tomography (Extended Data Figs. 5–7). This analysis revealed that (1) the interparticle centre-to-centre distance within the Au·TMA/ATP aggregates is shorter than that for the Au·TMA/P3O105– aggregates (8.08 ± 0.07 versus 8.27 ± 0.03 nm, in agreement with the SAXS results) and (2) the number of nearest NP neighbours is larger within the Au·TMA/ATP aggregates (7.4 ± 0.5, compare with 6.4 ± 0.8 for Au·TMA/P3O105–). Taken together, these results indicate that the Au·TMA/ATP aggregates have a more compact nature, which can be attributed to the incorporation of ATP’s nucleoside group within the organic monolayer on the NPs (as discussed above in the context of the SAXS results). Importantly, such an intercalation would render Au·TMA/ATP aggregates less dynamic, which can explain both (1) their resistance towards further aggregation and (2) their enhanced stability against enzymatic hydrolysis (that is, any excess (unbound) ATP is consumed first; we note that the disassembly profile in Fig. 6h is remarkably similar to typical assembly profiles (for example, in Fig. 1d) analysed backwards). In contrast, in the Au·TMA/P3O105– system, the enzyme discriminates less between free and NP-bound P3O105–: both are consumed at similar rates, which explains the disassembly profile shown in Fig. 6h.
Finally, we hypothesized that the lifetimes of the out-of-equilibrium NP aggregates could be controlled by the amount of added stimulus (green in Fig. 6d). Figure 6k shows the dependence of the λSPR value on Au·TMA following the addition of increasing amounts of ATP. The rapid disassembly of the NP aggregates commenced about 20 minutes after adding 13.5 nmol ATP versus as long as about 180 minutes after adding the stimulus (40.5 nmol). The behaviour of our system is reminiscent of the reversible formation of actin filaments64, which similarly assemble (from a globular protein G-actin) in the presence of ATP. Within these assemblies, ATP is rapidly hydrolysed65, and they need to be constantly resupplied with ATP to remain in the assembled, out-of-equilibrium state. In addition, our system allows for an independent way to control the lifetimes of the dynamic NP aggregates, which is based on varying the concentration (activity) of the enzyme. As Fig. 6l shows, aggregates generated by the addition of 27 nmol ATP could persist for periods of between 5 and 200 minutes, depending on the concentration of apyrase (~3–22 units of the enzyme per millilitre).
Conclusions
In sum, we investigated electrostatic interactions across the molecular and nanoscopic length scales, focusing on a model system of negatively charged small molecules and positively charged NPs. We found that small molecules with three (or more) charges could mediate attractive interactions between oppositely charged NPs, whereas those that bear one or two charges were unable to do so. These results could be rationalized by the Schulze–Hardy rule applied to a system of small NPs. The titration of charged NPs with oppositely charged small-molecule ions and vice versa demonstrated that our system combines the characteristics of molecular-scale and nanoscale systems, depending on the order of addition. MD simulations revealed that oligoanions that hold NPs together behave like a ‘dynamic ionic glue’, and thus facilitate structural transformations of the NP aggregates. Our results indicate that co-crystallization of charged NPs with oppositely charged small molecules, over one order of magnitude smaller in size, can give rise to colloidal crystals of a quality previously only thought to arise from co-assembling oppositely charged entities of similar sizes. Based on the above findings, we conceived a DSA system whereby NPs exist in the aggregated state only under a continuous supply of multiply charged anions, which are constantly hydrolysed into smaller anions. These results open up several avenues for further research. First, we anticipate that the here-disclosed method to crystallize NPs, based on the spontaneous decomposition of a volatile salt, will provide important insights into the underlying crystallization mechanisms. Second, the finding that the molecular ions within NP/ion aggregates exhibit mobility suggests that these aggregates may behave, and will be investigated, as ionic conductors. Third, it will be interesting to integrate metastable-state photoacids within our system of NP/trianion aggregates; the light-induced proton release can be used to protonate the trianion, and thus reversibly toggle between a trianion (in the dark; induces NP aggregation) and a dianion (under light; no aggregation), and consequently disassemble and reassemble the NP aggregates for multiple cycles. Finally, the ATP-mediated DSA system represents a unique example of a system composed of biocompatible components and one that operates in water, which thus brings us closer to interfacing dynamically self-assembling NPs with biological environments.
Methods
General information
All the chemicals were of analytical grade and were used as received. SEM was carried out on a Zeiss Ultra 55 microscope (operating at 10 kV unless indicated otherwise). TEM was carried out on a JEOL JEM-2100 microscope (operating at 200 kV). Ultraviolet–visible absorption spectra were recorded on a Shimadzu UV-2700 spectrophotometer. 1H NMR spectra were recorded on a Bruker Avance III 400 MHz NMR spectrometer (30 scans, relaxation delay of 20 s). Dynamic light scattering measurements were performed on a Zetasizer Nano ZS (Malvern). SAXS measurements were carried out at the 12-ID-B beamline of the Advanced Photon Source (APS), Argonne National Laboratory. Aqueous suspensions of crystalline NP aggregates were placed inside quartz capillaries. Each sample was exposed to X-ray beams with an energy of 14 keV for 1 s. Scattered photons were counted with a Pilatus2M detector located about 2 m downstream of the sample. Collected 2D SAXS images were azimuthally averaged with the software provided at the beamline. The diffraction patterns were simulated as reported elsewhere66,67. For the simulation, particle sizes were determined from solution SAXS measurements. The diffraction patterns were indexed by a custom-built software and the space groups were determined to yield the highest symmetry, assuming perfectly spherical particles. The Debye–Waller factor and microstrain used for the simulation were about 2.5 and 1.0%, respectively. The domain size was approximated to about 500 nm.
Molecular dynamics simulations
TMA-functionalized Au NPs and anions (citrate and hydrogen phosphate HPO42–) were built and simulated at two different molecular resolutions, AA and CG, where the resolution in the CG models is ~5 Å (Supplementary Fig. 7). All the AA and CG simulations were conducted using GROMACS 2018.6 software68 patched with the PLUMED 2 plugin69. Further details are provided in Supplementary Section 4.
Preparation of crystalline assemblies of positively charged nanoparticles and small anions
Supracrystals of TMA-functionalized Au NPs (Au·TMA) and multiply charged anions (Supplementary Fig. 4) were prepared by slowly decreasing the ionic strength of the solution by the spontaneous decomposition of (NH4)2CO3 (see the scheme in Fig. 4a). In a typical experiment, Au·TMA dissolved in water were treated with an aqueous solution of a multiply charged anion under vigorous shaking until the NPs’ λSPR plateaued (Fig. 1d and Supplementary Fig. 5a). The resulting aggregates were collected by centrifugation, washed twice with deionized water and dispersed in a small volume (typically 200 μl) of a 2.5 M aqueous solution of (NH4)2CO3, which resulted in a solution of well-dispersed NPs. The sample was left for 24 h, which resulted in the quantitative precipitation of the NPs in the form of colloidal crystals. Representative SEM images of Au·TMA co-crystallized with different multiply charged anions are shown in Fig. 4b–h and Extended Data Fig. 2.
Preparation of crystalline assemblies of negatively charged nanoparticles and small cations
Supracrystals of MUS-functionalized Au NPs (Au·MUS) and trications (Supplementary Fig. 20) were prepared by slowly decreasing the ionic strength of the solution by the spontaneous decomposition of (NH4)2CO3 (see the scheme in Fig. 4a). In a typical experiment, Au·MUS dissolved in water was treated with an aqueous solution of OMA3+ under vigorous shaking until the NPs’ λSPR plateaued (Fig. 5c). The aggregates that resulted were collected by centrifugation, washed twice with deionized water and dispersed in a small volume (typically 200 μl) of a 0.5 M aqueous solution of (NH4)2CO3, which resulted in a solution of well-dispersed NPs. The sample was left for 24 h, which resulted in the quantitative precipitation of the NPs in the form of colloidal crystals. Representative SEM images of Au·MUS co-crystallized with OMA3+ are shown in Fig. 5e,f and Extended Data Fig. 4.
Cryo-TEM analysis of aggregates of charged nanoparticles and oppositely charged small ions
Aggregates of 4.7 nm Au·TMA and P3O105– and aggregates of 4.7 nm Au·TMA and ATP were first prepared by mixing 64 nmol Au·TMA (in terms of surface TMA ligands) in 100 μl of water with 12.8 nmol P3O105– and 16 nmol ATP, both dissolved in 5 μl of water. Immediately thereafter, TEM specimens were prepared by transferring 2.5 μl of aqueous suspensions of the NP aggregates onto glow-discharged Quantifoil Cu 300-mesh R 2/1 or R 3.5/1 holey carbon grids, blotted for 3 s at 100% humidity, and plunge frozen in liquid ethane cooled by liquid nitrogen using a Vitrobot plunger (Thermo Fisher Scientific). The grids were loaded onto a Talos Arctica electron microscope (Thermo Fisher Scientific) and imaged under liquid nitrogen temperature. Cryo-TEM and cryo-STEM images were taken under low-dose conditions at an acceleration voltage of 200 kV. TEM images were recorded with a Gatan OneView camera (Gatan, Inc.); STEM images were collected with a bottom-mount bright-field detector (Thermo Fisher Scientific). Cryo-STEM tomograms were collected by tilting the sample along a single axis that spanned a tilt range from –60 up to 60° with a tilt increment of 2°. 2k × 2k scan frames were recorded with a probe semiconvergence angle of 1.3 mrad, a beam current of approximately 10 pA, a sampling rate of 0.60 nm per pixel and a dwell time of 5 μs per pixel, resulting in an exposure of approximately 9 electrons per Å2 per frame. These settings were kept constant for all the tomograms. Tomograms were reconstructed using the iterative simultaneous reconstruction technique. To avoid air–water interface artefacts, we analysed only those structures that were located in the bulk of the cryo-STEM tomography samples that had thicknesses of 200-400 nm. The 3D reconstruction was done after cross-correlation alignment and displacement refinement using an iterative feedback loop algorithm, as described before70. Quantitative order analysis was based on computational procedures described in detail in a previous publication71.
Data availability
All the data supporting the findings of this study are available within the main text of the paper, the Supplementary Information and also from the corresponding author on request. Source data are provided with this paper.
References
Sergeev, G. B. & Klabunde, K. J. Nanochemistry 2nd edn (Elsevier, 2013).
Ozin, G. A., Arsenault, A. & Cademartiri, L. Nanochemistry: A Chemical Approach to Nanomaterials 2nd edn (RSC Publishing, 2008).
Walter, M. et al. A unified view of ligand-protected gold clusters as superatom complexes. Proc. Natl Acad. Sci. USA 105, 9157–9162 (2008).
Bedanta, S. & Kleemann, W. Supermagnetism. J. Phys. D 42, 013001 (2009).
Morup, S., Hansen, M. F. & Frandsen, C. Magnetic interactions between nanoparticles. Beilstein J. Nanotech. 1, 182–190 (2010).
Song, L. & Deng, Z. Valency control and functional synergy in DNA-bonded nanomolecules. ChemNanoMat 3, 698–712 (2017).
Wei, Y., Bishop, K. J. M., Kim, J., Soh, S. & Grzybowski, B. A. Making use of bond strength and steric hindrance in nanoscale ‘synthesis’. Angew. Chem. Int. Ed. 48, 9477–9480 (2009).
Liu, K. et al. Step-growth polymerization of inorganic nanoparticles. Science 329, 197–200 (2010).
Liu, K. et al. Copolymerization of metal nanoparticles: a route to colloidal plasmonic copolymers. Angew. Chem. Int. Ed. 53, 2648–2653 (2014).
Klinkova, A., Thérien-Aubin, H., Choueiri, R. M., Rubinstein, M. & Kumacheva, E. Colloidal analogs of molecular chain stoppers. Proc. Natl Acad. Sci. USA 110, 18775–18779 (2013).
Shevchenko, E. V., Talapin, D. V., Kotov, N. A., O’Brien, S. & Murray, C. B. Structural diversity in binary nanoparticle superlattices. Nature 439, 55–59 (2006).
Udayabhaskararao, T. et al. Tunable porous nanoallotropes prepared by post-assembly etching of binary nanoparticle superlattices. Science 358, 514–518 (2017).
Wang, S. et al. Colloidal crystal ‘alloys’. J. Am. Chem. Soc. 141, 20443–20450 (2019).
Girard, M. et al. Particle analogs of electrons in colloidal crystals. Science 364, 1174–1178 (2019).
Vasquez, Y., Henkes, A. E., Bauer, J. C. & Schaak, R. E. Nanocrystal conversion chemistry: a unified and materials-general strategy for the template-based synthesis of nanocrystalline solids. J. Solid State Chem. 181, 1509–1523 (2008).
Krishnadas, K. R. et al. Interparticle reactions: an emerging direction in nanomaterials chemistry. Acc. Chem. Res. 50, 1988–1996 (2017).
Yin, Y. et al. Formation of hollow nanocrystals through the nanoscale Kirkendall effect. Science 304, 711–714 (2004).
Son, D. H., Hughes, S. M., Yin, Y. & Alivisatos, A. P. Cation exchange reactions in ionic nanocrystals. Science 306, 1009–1012 (2004).
Park, J., Zheng, H., Jun, Y.-w & Alivisatos, A. P. Hetero-epitaxial anion exchange yields single-crystalline hollow nanoparticles. J. Am. Chem. Soc. 131, 13943–13945 (2009).
Skrabalak, S. E. et al. Gold nanocages: synthesis, properties, and applications. Acc. Chem. Res. 41, 1587–1595 (2008).
Li, H. et al. Sequential cation exchange in nanocrystals: preservation of crystal phase and formation of metastable phases. Nano Lett. 11, 4964–4970 (2011).
Hong, S., Choi, Y. & Park, S. Shape control of Ag shell growth on Au nanodisks. Chem. Mater. 23, 5375–5378 (2011).
Buck, M. R. & Schaak, R. E. Emerging strategies for the total synthesis of inorganic nanostructures. Angew. Chem. Int. Ed. 52, 6154–6178 (2013).
Kalsin, A. M. et al. Electrostatic self-assembly of binary nanoparticle crystals with a diamond-like lattice. Science 312, 420–424 (2006).
Kalsin, A. M., Kowalczyk, B., Smoukov, S. K., Klajn, R. & Grzybowski, B. A. Ionic-like behavior of oppositely charged nanoparticles. J. Am. Chem. Soc. 128, 15046–15047 (2006).
Kalsin, A. M. & Grzybowski, B. A. Controlling the growth of ‘ionic’ nanoparticle supracrystals. Nano Lett. 7, 1018–1021 (2007).
Wang, L. Y., Albouy, P. A. & Pileni, M. P. Synthesis and self-assembly behavior of charged Au nanocrystals in aqueous solution. Chem. Mater. 27, 4431–4440 (2015).
Kostiainen, M. A. et al. Electrostatic assembly of binary nanoparticle superlattices using protein cages. Nat. Nanotechnol. 8, 52–56 (2013).
Liljeström, V., Seitsonen, J. & Kostiainen, M. A. Electrostatic self-assembly of soft matter nanoparticle cocrystals with tunable lattice parameters. ACS Nano 9, 11278–11285 (2015).
Hassinen, J., Liljeström, V., Kostiainen, M. A. & Ras, R. H. A. Rapid cationization of gold nanoparticles by two-step phase transfer. Angew. Chem. Int. Ed. 54, 7990–7993 (2015).
Laio, A. & Parrinello, M. Escaping free-energy minima. Proc. Natl Acad. Sci. USA 99, 12562–12566 (2002).
Barducci, A., Bussi, G. & Parrinello, M. Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100, 020603 (2008).
Beyeh, N. K. et al. Crystalline cyclophane–protein cage frameworks. ACS Nano 12, 8029–8036 (2018).
Schulze, H. Schwefelarsen in wässriger lösung. J. Prakt. Chem. 25, 431–452 (1882).
Hardy, W. B. A preliminary investigation of the conditions which determine the stability of irreversible hydrosols. Proc. R. Soc. Lond. 66, 110–125 (1900).
Trefalt, G., Szilágyi, I. & Borkovec, M. Schulze–Hardy rule revisited. Colloid Polym. Sci. 298, 961–967 (2020).
Gasparotto, P., Meißner, R. H. & Ceriotti, M. Recognizing local and global structural motifs at the atomic scale. J. Chem. Theory Comput. 14, 486–498 (2018).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Gasparotto, P., Bochicchio, D., Ceriotti, M. & Pavan, G. M. Identifying and tracking defects in dynamic supramolecular polymers. J. Phys. Chem. B 124, 589–599 (2020).
Mackay, A. L. A dense non-crystallographic packing of equal spheres. Acta Crystallogr. 15, 916–918 (1962).
Garzoni, M., Cheval, N., Fahmi, A., Danani, A. & Pavan, G. M. Ion-selective controlled assembly of dendrimer-based functional nanofibers and their ionic-competitive disassembly. J. Am. Chem. Soc. 134, 3349–3357 (2012).
Astachov, V. et al. In situ functionalization of self-assembled dendrimer nanofibers with cadmium sulfide quantum dots through simple ionic-substitution. New J. Chem. 40, 6325–6331 (2016).
Julin, S. et al. DNA origami directed 3D nanoparticle superlattice via electrostatic assembly. Nanoscale 11, 4546–4551 (2019).
House, J. E. A TG study of the kinetics of decomposition of ammonium carbonate and ammonium bicarbonate. Thermochim. Acta 40, 225–233 (1980).
Lofton, C. & Sigmund, W. Mechanisms controlling crystal habits of gold and silver colloids. Adv. Funct. Mater. 15, 1197–1208 (2005).
Wang, D. et al. How and why nanoparticle’s curvature regulates the apparent pKa of the coating ligands. J. Am. Chem. Soc. 133, 2192–2197 (2011).
Boyer, P. D. Energy, life, and ATP (Nobel Lecture). Angew. Chem. Int. Ed. 37, 2297–2307 (1998).
van Rossum, S. A. P., Tena-Solsona, M., van Esch, J. H., Eelkema, R. & Boekhoven, J. Dissipative out-of-equilibrium assembly of man-made supramolecular materials. Chem. Soc. Rev. 46, 5519–5535 (2017).
Singh, N., Formon, G. J. M., De Piccoli, S. & Hermans, T. M. Devising synthetic reaction cycles for dissipative non-equilibrium self-assembly. Adv. Mater. 32, 1906834 (2020).
Ragazzon, G. & Prins, L. J. Energy consumption in chemical fuel-driven self-assembly. Nat. Nanotech. 13, 882–889 (2018).
Wang, G. & Liu, S. Strategies to construct a chemical-fuel-driven self-assembly. ChemSystemsChem 2, e1900046 (2020).
Weißenfels, M., Gemen, J. & Klajn, R. Dissipative self-assembly: fueling with chemicals versus light. Chem 7, 23–37 (2021).
Grötsch, R. K. et al. Dissipative self-assembly of photoluminescent silicon nanocrystals. Angew. Chem. Int. Ed. 57, 14608–14612 (2018).
Grötsch, R. K. et al. Pathway dependence in the fuel-driven dissipative self-assembly of nanoparticles. J. Am. Chem. Soc. 141, 9872–9878 (2019).
van Ravensteijn, B. G. P., Hendriksen, W. E., Eelkema, R., van Esch, J. H. & Kegel, W. K. Fuel-mediated transient clustering of colloidal building blocks. J. Am. Chem. Soc. 139, 9763–9766 (2017).
Hsu, C. C. et al. Role of synaptic vesicle proton gradient and protein phosphorylation on ATP-mediated activation of membrane-associated brain glutamate decarboxylase. J. Biol. Chem. 274, 24366–24371 (1999).
Boekhoven, J. et al. Dissipative self-assembly of a molecular gelator by using a chemical fuel. Angew. Chem. Int. Ed. 49, 4825–4828 (2010).
Leira-Iglesias, J., Sorrenti, A., Sato, A., Dunne, P. A. & Hermans, T. M. Supramolecular pathway selection of perylenediimides mediated by chemical fuels. Chem. Commun. 52, 9009–9012 (2016).
Wang, G., Sun, J., An, L. & Liu, S. Fuel-driven dissipative self-assembly of a supra-amphiphile in batch reactor. Biomacromolecules 19, 2542–2548 (2018).
Zhang, Y. X. & Zeng, H. C. Surfactant-mediated self-assembly of Au nanoparticles and their related conversion to complex mesoporous structures. Langmuir 24, 3740–3746 (2008).
Klajn, R. et al. Bulk synthesis and surface patterning of nanoporous metals and alloys from supraspherical nanoparticle aggregates. Adv. Funct. Mater. 18, 2763–2769 (2008).
Heo, K., Miesch, C., Emrick, T. & Hayward, R. C. Thermally reversible aggregation of gold nanoparticles in polymer nanocomposites through hydrogen bonding. Nano Lett. 13, 5297–5302 (2013).
Stolzenburg, P., Hämisch, B., Richter, S., Huber, K. & Garnweitner, G. Secondary particle formation during the nonaqueous synthesis of metal oxide nanocrystals. Langmuir 34, 12834–12844 (2018).
Reisler, E. & Egelman, E. H. Actin structure and function: what we still do not understand. J. Biol. Chem. 282, 36133–36137 (2007).
Pfaendtner, J., Lyman, E., Pollard, T. D. & Voth, G. A. Structure and dynamics of the actin filament. J. Mol. Biol. 396, 252–263 (2010).
Senesi, A. J. & Lee, B. Small-angle scattering of particle assemblies. J. Appl. Crystallogr. 48, 1172–1182 (2015).
Macfarlane, R. J. et al. Nanoparticle superlattice engineering with DNA. Science 334, 204–208 (2011).
Abraham, M. J. et al. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2, 19–25 (2015).
Tribello, G. A., Bonomi, M., Branduardi, D., Camilloni, C. & Bussi, G. PLUMED 2: new feathers for an old bird. Comput. Phys. Commun. 185, 604–613 (2014).
Houben, L. & Bar Sadan, M. Refinement procedure for the image alignment in high-resolution electron tomography. Ultramicroscopy 111, 1512–1520 (2011).
Houben, L., Weissman, H., Wolf, S. G. & Rybtchinski, B. A mechanism of ferritin crystallization revealed by cryo-STEM tomography. Nature 579, 540–543 (2020).
Acknowledgements
This work was supported by the European Research Council (ERC) (grants 820008 to R.K. and 818776 to G.M.P.), the Minerva Foundation with funding from the Federal German Ministry for Education and Research and the Swiss National Science Foundation (grants 200021_175735 and IZLIZ2_183336 to G.M.P.). We acknowledge funding from the European Union’s Horizon 2020 Research and Innovation Program under the Marie Skłodowska-Curie grant agreement no. 812868. Z.C. acknowledges support from the Planning and Budgeting Committee of the Council for Higher Education, the Koshland Foundation and a McDonald–Leapman grant. The authors acknowledge the computational resources provided by the Swiss National Supercomputing Centre (CSCS). The support of the Irving and Cherna Moskowitz Center for Nano and Bio-Nano Imaging is gratefully acknowledged. This research used resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract no. DE-AC02-06CH11357. Extraordinary facility operations were supported in part by the DOE Office of Science through the National Virtual Biotechnology Laboratory, a consortium of DOE national laboratories focused on the response to COVID-19, with funding provided by the Coronavirus CARES Act.
Author information
Authors and Affiliations
Contributions
T.B. synthesized positively charged NPs, studied their interactions with oligoanions and developed a method to prepare crystalline NP aggregates. A.G. and C.P. performed the computational studies. J.G. developed the reverse system of negatively charged NPs and oligocations. B.L. performed and analysed the SAXS measurements. N.E. and L.H. performed cryo-STEM imaging and analysis. Z.C. contributed to the characterization of the NPs. R.K. supervised the project, coordinating with G.M.P., who supervised the computational studies. R.K. prepared the manuscript, with contributions from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Chemistry thanks Tobias Kraus, Asaph Widmer-Cooper and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Dependence of the titration behavior on nanoparticle size.
Differently sized TMA-functionalized Au NPs (4.8 nm, 8.8 nm, and 13.1 nm) at the same overall concentration of TMA in solution were titrated with the same solution of EDTA3– (the NPs were prepared analogously to those described in the Methods section). a, Left: Change in the position of Au·TMA’s SPR peak as a function of amount of EDTA3– added. In all cases, the amount of NP-adsorbed TMA was 20 nmol. The dashed red line denotes the point of electroneutrality (6.7 nmol of triply charged EDTA). Right: Relative dimensions of Au·TMA used in titration experiments. b, Normalized position of Au·TMA’s SPR peak as a function of amount of EDTA3– added (replotted from a). The normalized data show that the titration profiles are nearly the same irrespective of the NP size, indicating that the interparticle interactions are governed predominantly by electrostatics. The dashed red line denotes the point of electroneutrality (6.7 nmol of triply charged EDTA).
Extended Data Fig. 2 Representative SEM images of colloidal crystals co-assembled from TMA-functionalized Au NPs and various multiply charged anions.
The following anions were used: a–c, EDTA3–; d–j, citrate3–; k, l, pyrophosphate4–; m–s, triphosphate5–; t, u, trimetaphosphate3–; v, w, hexametaphosphate6–; x–z, ATP4–. The size of the NPs was 4.7 nm (panels n–r), 7.4 nm (panels a–f, j–m, and s–z), and 11.4 nm (panels g–i). In all cases, the counterion was Na+.
Extended Data Fig. 3 Nanoparticle packing on the faces of colloidal crystals.
SEM images of crystals co-assembled from TMA-functionalized 4.7 nm Au NPs and ATP. The magnified images in (b) and (e) show the hexagonal packing of NPs characteristic of the (111) facet of the face-centered cubic (fcc) structure. The magnified image in (g) shows the cubic packing of NPs characteristic of the (100) facet of the fcc structure.
Extended Data Fig. 4 SEM images of colloidal crystals co-assembled from negatively charged NPs and an organic trication.
The crystals were prepared using MUS-functionalized 4.7 nm Au NPs and triply charged cations, OMA3+, as described in the Methods section.
Extended Data Fig. 5 Cryo-STEM images of aggregates of TMA-functionalized Au NPs and P3O105− or ATP.
a, Contrast-inverted bright-field cryo-STEM images of Au·TMA/P3O105− aggregates. Reconstruction and analysis of the aggregates denoted by circles are shown in Extended Data Fig. 6. b, Contrast-inverted bright-field cryo-STEM image of Au·TMA/ATP aggregates. Reconstruction and analysis of the aggregates denoted by circles are shown in Extended Data Fig. 7. All panels show single images at zero tilt, part of a tilt series spanning the tilt range of 60°.
Extended Data Fig. 6 Reconstruction and analysis of Au·TMA/P3O105− aggregates.
Labels a–d correspond to the locations indicated with the same labels in Extended Data Fig. 5. Left panel: ‘Atomistic’ models of the aggregates obtained after 3D reconstruction and particle coordinate refinement. Middle panel: Numbers of nearest neighbors in the first coordination shell in a color-coded representation for each NP. Average number of nearest neighbors = 6.4 (±0.8) (measured on ten different aggregates). Right panel: Pair correlation functions; the nearest-neighbor distance, Δ = 8.27 (±0.03) nm.
Extended Data Fig. 7 Reconstruction and analysis of Au·TMA/ATP aggregates.
Labels a–d correspond to the locations indicated with the same labels in Extended Data Fig. 5. First panel: Contrast-inverted bright-field cryo-STEM images of individual Au·TMA/ATP aggregates. Second panel: ‘Atomistic’ models of the aggregates obtained after 3D reconstruction and particle coordinate refinement. Third panel: Numbers of nearest neighbors in the first coordination shell in a color-coded representation for each NP. Average number of nearest neighbors = 7.4 (±0.5) (measured on five different aggregates). Fourth panel: Pair correlation functions; the nearest-neighbor distance, Δ = 8.08 (±0.07) nm.
Supplementary information
Supplementary Information
Detailed description of experimental and computational procedures, Supplementary Figs. 1–40 and references.
Supplementary Video 1
CG-MD simulation of citrate-mediated self-assembly of two TMA-decorated Au NPs.
Supplementary Video 2
CG-MD simulation of citrate-mediated self-assembly of four TMA-decorated Au NPs.
Source data
Source Data Fig. 1
Statistical source data for Fig. 1d,e.
Source Data Fig. 2
Statistical source data for Fig. 2b,d.
Source Data Fig. 4
Statistical source data for Fig. 4j,l.
Source Data Fig. 5
Statistical source data for Fig. 5c,d.
Source Data Fig. 6
Statistical source data for Fig. 6c,d,f–h,k,l.
Rights and permissions
About this article
Cite this article
Bian, T., Gardin, A., Gemen, J. et al. Electrostatic co-assembly of nanoparticles with oppositely charged small molecules into static and dynamic superstructures. Nat. Chem. 13, 940–949 (2021). https://doi.org/10.1038/s41557-021-00752-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41557-021-00752-9
This article is cited by
-
Building blocks of order: block copolymer micelles and colloidal particles in complex packing structures
Journal of Polymer Research (2024)
-
A simple self-assembling system of melittin for hepatoma treatment
Cancer Nanotechnology (2023)
-
Dynamic active-site induced by host-guest interactions boost the Fenton-like reaction for organic wastewater treatment
Nature Communications (2023)
-
Mechanosensitive non-equilibrium supramolecular polymerization in closed chemical systems
Nature Communications (2023)
-
Machine learning of atomic dynamics and statistical surface identities in gold nanoparticles
Communications Chemistry (2023)