Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Hydroxide diffuses slower than hydronium in water because its solvated structure inhibits correlated proton transfer

Nature Chemistry volume 10, pages 413–419 (2018)Cite this article

Subjects

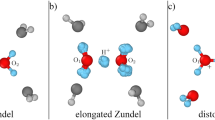
Abstract

Proton transfer via hydronium and hydroxide ions in water is ubiquitous. It underlies acid–base chemistry, certain enzyme reactions, and even infection by the flu. Despite two centuries of investigation, the mechanism underlying why hydroxide diffuses slower than hydronium in water is still not well understood. Herein, we employ state-of-the-art density-functional-theory-based molecular dynamics—with corrections for non-local van der Waals interactions, and self-interaction in the electronic ground state—to model water and hydrated water ions. At this level of theory, we show that structural diffusion of hydronium preserves the previously recognized concerted behaviour. However, by contrast, proton transfer via hydroxide is less temporally correlated, due to a stabilized hypercoordination solvation structure that discourages proton transfer. Specifically, the latter exhibits non-planar geometry, which agrees with neutron-scattering results. Asymmetry in the temporal correlation of proton transfer leads to hydroxide diffusing slower than hydronium.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Electronic structure of the solvated water molecule and water ions from PBE0-TS trajectories.
Fig. 2: Frequency of proton transfer events with three exchange–correlation functionals (PBE, PBE-TS, and PBE0-TS).
Fig. 3: Free energy maps for water wire compression and double proton jumps with the PBE0-TS functional.
Fig. 4: Solvation structures of OH–(aq) with three functional approximations (PBE, PBE-TS, and PBE0-TS).

References

  1. Hückel, E. 3. Einzelvorträge: elektrochemie. theorie der beweglichkeiten des wasserstoff‐und hydroxylions in wässriger lösung. Z. Elektrochem. Angew. Phys. Chem. 34, 546–562 (1928).

    Google Scholar 

  2. Bernal, J. & Fowler, R. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Phys. Chem. 1, 515–548 (1933).

    Article  CAS  Google Scholar 

  3. de Grotthuss, C. Theory of decomposition of liquids by electrical currents. [in French] Ann. Chim. 58, 54–74 (1806).

    Google Scholar 

  4. Agmon, N. et al. Protons and hydroxide ions in aqueous systems. Chem. Rev. 116, 7642–7672 (2016).

    Article  CAS  PubMed  Google Scholar 

  5. Halle, B. & Karlström, G. Prototropic charge migration in water. Part 2. Interpretation of nuclear magnetic resonance and conductivity data in terms of model mechanisms. J. Chem. Soc. Faraday Trans. 2 79, 1047–1073 (1983).

    Article  CAS  Google Scholar 

  6. Weingärtner, H. & Chatzidimttriou-Dreismann, C. Anomalous H+ and D+ conductance in H2O–D2O mixtures. Nature 346, 548–550 (1990).

    Article  Google Scholar 

  7. Sluyters, J. & Sluyters-Rehbach, M. The mechanism of the hydrogen ion conduction in liquid light and heavy water derived from the temperature dependence of their limiting conductivities. J. Phys. Chem. B 114, 15582–15589 (2010).

    Article  CAS  PubMed  Google Scholar 

  8. Halle, B. & Karlström, G. Prototropic charge migration in water. Part 1. Rate constants in light and heavy water and in salt solution from oxygen-17 spin relaxation. J. Chem. Soc. Faraday Trans. 2 79, 1031–1046 (1983).

    Article  CAS  Google Scholar 

  9. Car, R. & Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471 (1985).

    Article  CAS  PubMed  Google Scholar 

  10. Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).

    Article  Google Scholar 

  11. Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).

    Article  Google Scholar 

  12. Tuckerman, M. E., Laasonen, K., Sprik, M. & Parrinello, M. Ab initio simulations of water and water ions. J. Phys. Condens. Matter 6, A93 (1994).

    Article  CAS  Google Scholar 

  13. Wicke, E., Eigen, M. & Ackermann, T. Über den zustand des protons (hydroniumions) in wäβriger lösung. Z. Phys. Chem. 1, 340 (1954).

    Article  Google Scholar 

  14. Eigen, M. Proton transfer, acid–base catalysis, and enzymatic hydrolysis. Part I: Elementary processes. Angew. Chem. Int. Ed. 3, 1–19 (1964).

    Article  Google Scholar 

  15. Zundel, G. & Metzger, H. Energiebänder der tunnelnden überschuß-protonen in flüssigen säuren. Eine IR-spektroskopische untersuchung der natur der gruppierungen H5O2 +. Z. Phys. Chem. 58, 225–245 (1968).

    Article  CAS  Google Scholar 

  16. Tse, Y.-L. S., Knight, C. & Voth, G. A. An analysis of hydrated proton diffusion in ab initio molecular dynamics. J. Chem. Phys. 142, 014104 (2015).

    Article  CAS  PubMed  Google Scholar 

  17. Thämer, M., De Marco, L., Ramasesha, K., Mandal, A. & Tokmakoff, A. Ultrafast 2D IR spectroscopy of the excess proton in liquid water. Science 350, 78–82 (2015).

    Article  CAS  PubMed  Google Scholar 

  18. Decka, D., Schwaab, G. & Havenith, M. A. THz/FTIR fingerprint of the solvated proton: evidence for Eigen structure and Zundel dynamics. Phys. Chem. Chem. Phys. 17, 11898–11907 (2015).

    Article  CAS  PubMed  Google Scholar 

  19. Dahms, F. et al. The hydrated excess proton in the Zundel cation H5O2 +: the role of ultrafast solvent fluctuations. Angew. Chem. Int. Ed. 55, 10600–10605 (2016).

    Article  CAS  Google Scholar 

  20. Wolke, C. T. et al. Spectroscopic snapshots of the proton-transfer mechanism in water. Science 354, 1131–1135 (2016).

    Article  CAS  PubMed  Google Scholar 

  21. Dahms, F., Fingerhut, B. P., Nibbering, E. T., Pines, E. & Elsaesser, T. Large-amplitude transfer motion of hydrated excess protons mapped by ultrafast 2D IR spectroscopy. Science 357, 491–495 (2017).

    Article  CAS  PubMed  Google Scholar 

  22. Biswas, R., Carpenter, W., Fournier, J. A., Voth, G. A. & Tokmakoff, A. IR spectral assignments for the hydrated excess proton in liquid water. J. Phys. Chem. 146, 154507 (2017).

    Article  CAS  Google Scholar 

  23. Daly, C. A. et al. Decomposition of the experimental Raman and infrared spectra of acidic water into proton, special pair, and counter-ion contributions. J. Phys. Chem. Lett. 8, 5246–5252 (2017).

    Article  CAS  PubMed  Google Scholar 

  24. Botti, A., Bruni, F., Imberti, S., Ricci, M. & Soper, A. Solvation of hydroxyl ions in water. J. Phys. Chem. 119, 5001–5004 (2003).

    Article  CAS  Google Scholar 

  25. Aziz, E. F., Ottosson, N., Faubel, M., Hertel, I. V. & Winter, B. Interaction between liquid water and hydroxide revealed by core–hole de-excitation. Nature 455, 89–91 (2008).

    Article  CAS  PubMed  Google Scholar 

  26. Tuckerman, M. E., Chandra, A. & Marx, D. Structure and dynamics of OH–(aq). Acc. Chem. Res. 39, 151–158 (2006).

    Article  CAS  PubMed  Google Scholar 

  27. Marx, D. Proton transfer 200 years after von Grotthuss: insights from ab initio simulations. ChemPhysChem 7, 1848–1870 (2006).

    Article  PubMed  Google Scholar 

  28. Hassanali, A., Prakash, M. K., Eshet, H. & Parrinello, M. On the recombination of hydronium and hydroxide ions in water. Proc. Natl Acad. Sci. USA 108, 20410–20415 (2011).

    Article  PubMed  Google Scholar 

  29. Hassanali, A., Giberti, F., Cuny, J., Kühne, T. D. & Parrinello, M. Proton transfer through the water gossamer. Proc. Natl Acad. Sci. USA 110, 13723–13728 (2013).

    Article  PubMed  Google Scholar 

  30. Gillan, M. J., Alfè, D. & Michaelides, A. Perspective: how good is DFT for water? J. Phys. Chem. 144, 130901 (2016).

    Article  CAS  Google Scholar 

  31. Gaiduk, A. P., Gygi, F. & Galli, G. Density and compressibility of liquid water and ice from first-principles simulations with hybrid functionals. J. Phys. Chem. Lett. 6, 2902–2908 (2015).

    Article  CAS  PubMed  Google Scholar 

  32. Miceli, G., de Gironcoli, S. & Pasquarello, A. Isobaric first-principles molecular dynamics of liquid water with nonlocal van der Waals interactions. J. Chem. Phys. 142, 034501 (2015).

    Article  CAS  Google Scholar 

  33. Marx, D., Chandra, A. & Tuckerman, M. E. Aqueous basic solutions: hydroxide solvation, structural diffusion, and comparison to the hydrated proton. Chem. Rev. 110, 2174–2216 (2010).

    Article  CAS  PubMed  Google Scholar 

  34. Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Phys. Chem. 105, 9982–9985 (1996).

    Article  CAS  Google Scholar 

  35. Wu, X. F., Selloni, A. & Car, R. Order-N implementation of exact exchange in extended insulating systems. Phys. Rev. B 79, 085102 (2009).

    Article  CAS  Google Scholar 

  36. Tkatchenko, A. & Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009).

    Article  CAS  PubMed  Google Scholar 

  37. DiStasio, R. A.  Jr, Santra, B., Li, Z., Wu, X. & Car, R. The individual and collective effects of exact exchange and dispersion interactions on the ab initio structure of liquid water. J. Phys. Chem. 141, 084502 (2014).

    Article  CAS  Google Scholar 

  38. Crespo, Y. & Hassanali, A. Unveiling the Janus-like properties of OH–. J. Phys. Chem. Lett. 6, 272–278 (2015).

    Article  CAS  PubMed  Google Scholar 

  39. Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).

    Article  CAS  Google Scholar 

  40. Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419 (2012).

    Article  CAS  Google Scholar 

  41. Hassanali, A. A., Giberti, F., Sosso, G. C. & Parrinello, M. The role of the umbrella inversion mode in proton diffusion. Chem. Phys. Lett. 599, 133–138 (2014).

    Article  CAS  Google Scholar 

  42. Wang, F., Izvekov, S. & Voth, G. A. Unusual “amphiphilic” association of hydrated protons in strong acid solution. J. Am. Chem. Soc. 130, 3120–3126 (2008).

    Article  CAS  PubMed  Google Scholar 

  43. Iuchi, S., Chen, H., Paesani, F. & Voth, G. A. Hydrated excess proton at water−hydrophobic interfaces. J. Phys. Chem. B 113, 4017–4030 (2008).

    Article  CAS  Google Scholar 

  44. Tse, Y. L., Chen, C., Lindberg, G. E., Kumar, R. & Voth, G. A. Propensity of hydrated excess protons and hydroxide anions for the air–water interface. J. Am. Chem. Soc. 137, 12610 (2015).

    Article  CAS  PubMed  Google Scholar 

  45. Giberti, F. & Hassanali, A. The excess proton at the air–water interface: the role of instantaneous liquid interfaces. J. Chem. Phys. 146, 244703 (2017).

    Article  CAS  PubMed  Google Scholar 

  46. Woutersen, S. & Bakker, H. J. Ultrafast vibrational and structural dynamics of the proton in liquid water. Phys. Rev. Lett. 96, 138305 (2006).

    Article  CAS  PubMed  Google Scholar 

  47. Tielrooij, K. J., Timmer, R. L. A., Bakker, H. J. & Bonn, M. Structure dynamics of the proton in liquid water probed with terahertz time-domain spectroscopy. Phys. Rev. Lett. 102, 198303 (2009).

    Article  CAS  PubMed  Google Scholar 

  48. Marx, D., Tuckerman, M. E., Hutter, J. & Parrinello, M. The nature of the hydrated excess proton in water. Nature 397, 601–604 (1999).

    Article  CAS  Google Scholar 

  49. Chen, J., Li, X.-Z., Zhang, Q., Michaelides, A. & Wang, E. Nature of proton transport in a water-filled carbon nanotube and in liquid water. Phys. Chem. Chem. Phys. 15, 6344–6349 (2013).

    Article  CAS  PubMed  Google Scholar 

  50. Giberti, F., Hassanali, A. A., Ceriotti, M. & Parrinello, M. The role of quantum effects on structural and electronic fluctuations in neat and charged water. J. Phys. Chem. B 118, 13226–13235 (2014).

    Article  CAS  PubMed  Google Scholar 

  51. Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).

    Article  CAS  PubMed  Google Scholar 

  52. Troullier, N. & Martins, J. L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993–2006 (1991).

    Article  CAS  Google Scholar 

  53. Tassone, F., Mauri, F. & Car, R. Acceleration schemes for ab initio molecular-dynamics simulations and electronic-structure calculations. Phys. Rev. B 50, 10561 (1994).

    Article  CAS  Google Scholar 

  54. Martyna, G. J., Klein, M. L. & Tuckerman, M. E. Nosé–Hoover chains: the canonical ensemble via continuous dynamics. J. Phys. Chem. 97, 2635–2643 (1992).

    Article  Google Scholar 

  55. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).

    Article  CAS  PubMed  Google Scholar 

  56. Luzar, A. & Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 379, 55–57 (1996).

    Article  CAS  Google Scholar 

  57. Wang, Y. & Perdew, J. P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 44, 13298 (1991).

    Article  CAS  Google Scholar 

  58. Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098 (1988).

    Article  CAS  Google Scholar 

  59. Lee, C., Yang, W. & Parr, R. G. Development of the Colle–Salvetti correlation–energy formula into a functional of the electron density. Phys. Rev. B 37, 785 (1988).

    Article  CAS  Google Scholar 

  60. Boese, A. D., Doltsinis, N. L., Handy, N. C. & Sprik, M. New generalized gradient approximation functionals. J. Phys. Chem. 112, 1670–1678 (2000).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

This project was supported by US Department of Energy SciDAC under grant numbers DE-SC0008726 and DE-SC0008626 and partially supported by the Division of Materials Research (DMR) under Award DMR-1552287. R.A.D. acknowledges partial support from Cornell University through start-up funding and the Cornell Center for Materials Research (CCMR) with funding from the National Science Foundation (NSF) MRSEC programme (DMR-1719875). This research used resources of the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the US Department of Energy under contract number DE-AC02-06CH11357. This research also used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under contract number DE-AC02-05CH11231. X.W. is grateful for the useful discussions with D. Vanderbilt at Rutgers University and A. J. Shanahan at University Medical Center of Princeton.

Author information

Author notes

  1. These authors contributed equally: Mohan Chen, Lixin Zheng.

Authors and Affiliations

  1. Department of Physics, Temple University, Philadelphia, PA, USA

    Mohan Chen, Lixin Zheng, Michael L. Klein & Xifan Wu

  2. Department of Chemistry, Princeton University, Princeton, NJ, USA

    Biswajit Santra, Hsin-Yu Ko & Roberto Car

  3. Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, USA

    Robert A. DiStasio Jr

  4. Department of Chemistry, Temple University, Philadelphia, PA, USA

    Michael L. Klein

  5. Institute for Computational Molecular Science, Temple University, Philadelphia, PA, USA

    Michael L. Klein & Xifan Wu

  6. Department of Physics, Princeton University, Princeton, NJ, USA

    Roberto Car

Authors
  1. Mohan Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lixin Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Biswajit Santra
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hsin-Yu Ko
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Robert A. DiStasio Jr
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Michael L. Klein
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Roberto Car
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Xifan Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

X.W., R.C. and M.L.K. designed the project. M.C. and L.Z. carried out the simulations. M.C. and L.Z. performed the analysis. R.A.D., B.S. and H.-Y.K. developed methodologies in Quantum ESPRESSO. X.W., R.C., M.L.K. and R.A.D. wrote the manuscript. All authors contributed to the discussions and revisions of the manuscript.

Corresponding authors

Correspondence to Roberto Car or Xifan Wu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1 and 2; Supplementary Tables 1 and 2; Supplementary Methods and Discussion

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, M., Zheng, L., Santra, B. et al. Hydroxide diffuses slower than hydronium in water because its solvated structure inhibits correlated proton transfer. Nature Chem 10, 413–419 (2018). https://doi.org/10.1038/s41557-018-0010-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41557-018-0010-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing