Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Temporal and spatial topography of cell proliferation in cancer

Nature Cell Biology volume 24, pages 316–326 (2022)Cite this article

Subjects

Abstract

Proliferation is a fundamental trait of cancer cells, but its properties and spatial organization in tumours are poorly characterized. Here we use highly multiplexed tissue imaging to perform single-cell quantification of cell cycle regulators and then develop robust, multivariate, proliferation metrics. Across diverse cancers, proliferative architecture is organized at two spatial scales: large domains, and smaller niches enriched for specific immune lineages. Some tumour cells express cell cycle regulators in the (canonical) patterns expected of freely growing cells, a phenomenon we refer to as ‘cell cycle coherence’. By contrast, the cell cycles of other tumour cell populations are skewed towards specific phases or exhibit non-canonical (incoherent) marker combinations. Coherence varies across space, with changes in oncogene activity and therapeutic intervention, and is associated with aggressive tumour behaviour. Thus, multivariate measures from high-plex tissue images capture clinically significant features of cancer proliferation, a fundamental step in enabling more precise use of anti-cancer therapies.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: MPI is linked to clinical parameters.
Fig. 2: MPI reveals two proliferative domains of cancer proliferative architecture.
Fig. 3: A framework for inferring cell cycle dynamics from multiplexed imaging data.
Fig. 4: Extraction of cell cycle coherence metrics from multiplexed images of human cancer tissues.
Fig. 5: Coherence metrics are modulated by HER2 expression in human breast cancer tissues and HER2-driven mouse model of breast cancer.
Fig. 6: Coherence metrics change with treatment.
Fig. 7: Coherence metrics are associated with clinical outcome.

Similar content being viewed by others

Data availability

Images, generated datasets and corresponding analysis are available in the Synapse.org repository syn2230077174. Multiplexed images of human HER2 breast cancer used in Fig. 3a can be viewed in Minerva Story72,73 an interpretive guide for interacting with multiplexed tissue imaging data https://tinyurl.com/minerva-proliferation. Imaging data and other data supporting the findings of this study are available from the corresponding author on reasonable request.

Code availability

MATLAB codes used to process and analyse the p-CyCIF and t-CyCIF (shortened as ‘CyCIF’) and the codes used for ccD-CMD analysis are available at https://github.com/santagatalab.

References

  1. Hanahan, D. & Weinberg, R. A. Hallmarks of cancer: the next generation. Cell 144, 646–674 (2011).

    Article  CAS  PubMed  Google Scholar 

  2. Duval, K. et al. Modeling physiological events in 2D vs. 3D cell culture. Physiology 32, 266–277 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  3. Norton, L. A Gompertzian model of human breast cancer growth. Cancer Res. 48, 7067–7071 (1988).

    CAS  PubMed  Google Scholar 

  4. Norton, L., Simon, R., Brereton, H. D. & Bogden, A. E. Predicting the course of Gompertzian growth. Nature 264, 542–545 (1976).

    Article  CAS  PubMed  Google Scholar 

  5. Collins, V. P., Loeffler, R. K. & Tivey, H. Observations on growth rates of human tumors. Am. J. Roentgenol. Radium Ther. Nucl. Med 76, 988–1000 (1956).

    CAS  PubMed  Google Scholar 

  6. Black, J. R. M. & McGranahan, N. Genetic and non-genetic clonal diversity in cancer evolution. Nat. Rev. Cancer https://doi.org/10.1038/s41568-021-00336-2 (2021).

  7. Nia, H. T., Munn, L. L. & Jain, R. K. Physical traits of cancer. Science 370, eaaz0868 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  8. Lin, J.-R. et al. Highly multiplexed immunofluorescence imaging of human tissues and tumors using t-CyCIF and conventional optical microscopes. eLife 7, e31657 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  9. Nirmal, A. J. et al. The spatial landscape of progression and immunoediting in primary melanoma at single cell resolution. bioRxiv https://doi.org/10.1101/2021.05.23.445310 (2021).

  10. Aguirre-Ghiso, J. A. Models, mechanisms and clinical evidence for cancer dormancy. Nat. Rev. Cancer 7, 834–846 (2007).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. Inwald, E. C. et al. Ki-67 is a prognostic parameter in breast cancer patients: results of a large population-based cohort of a cancer registry. Breast Cancer Res Treat. 139, 539–552 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Lehr, H.-A. et al. Mitotic figure counts are significantly overestimated in resection specimens of invasive breast carcinomas. Mod. Pathol. 26, 336–342 (2013).

    Article  CAS  PubMed  Google Scholar 

  13. Cuylen-Haering, S. et al. Chromosome clustering by Ki-67 excludes cytoplasm during nuclear assembly. Nature 587, 285–290 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Sobecki, M. et al. The cell proliferation antigen Ki-67 organises heterochromatin. eLife 5, e13722 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  15. Bruno, S. & Darzynkiewicz, Z. Cell cycle dependent expression and stability of the nuclear protein detected by Ki-67 antibody in HL-60 cells. Cell Prolif. 25, 31–40 (1992).

    Article  CAS  PubMed  Google Scholar 

  16. Miller, I. et al. Ki67 is a graded rather than a binary marker of proliferation versus quiescence. Cell Rep. 24, 1105–1112.e5 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  17. Gerdes, J., Schwab, U., Lemke, H. & Stein, H. Production of a mouse monoclonal antibody reactive with a human nuclear antigen associated with cell proliferation. Int J. Cancer 31, 13–20 (1983).

    Article  CAS  PubMed  Google Scholar 

  18. Denkert, C. et al. Strategies for developing Ki67 as a useful biomarker in breast cancer. Breast 24, S67–S72 (2015).

    Article  PubMed  Google Scholar 

  19. Nielsen, T. O. et al. Assessment of Ki67 in breast cancer: updated recommendations from the international Ki67 in Breast Cancer Working Group. J Natl Cancer Inst https://doi.org/10.1093/jnci/djaa201 (2020).

  20. Rozenblatt-Rosen, O. et al. The Human Tumor Atlas Network: charting tumor transitions across space and time at single-cell resolution. Cell 181, 236–249 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Angelo, M. et al. Multiplexed ion beam imaging of human breast tumors. Nat. Med. 20, 436–442 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Giesen, C. et al. Highly multiplexed imaging of tumor tissues with subcellular resolution by mass cytometry. Nat. Methods 11, 417–422 (2014).

    Article  CAS  PubMed  Google Scholar 

  23. Goltsev, Y. et al. Deep profiling of mouse splenic architecture with CODEX multiplexed imaging. Cell 174, 968–981.e15 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  24. Bodenmiller, B. Multiplexed epitope-based tissue imaging for discovery and healthcare applications. Cell Syst. 2, 225–238 (2016).

    Article  CAS  PubMed  Google Scholar 

  25. Gookin, S. et al. A map of protein dynamics during cell-cycle progression and cell-cycle exit. PLoS Biol. 15, e2003268 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  26. Mahdessian, D. et al. Spatiotemporal dissection of the cell cycle with single-cell proteogenomics. Nature 590, 649–654 (2021).

    Article  CAS  PubMed  Google Scholar 

  27. Nishitani, H., Lygerou, Z., Nishimoto, T. & Nurse, P. The Cdt1 protein is required to license DNA for replication in fission yeast. Nature 404, 625–628 (2000).

    Article  CAS  PubMed  Google Scholar 

  28. McGarry, T. J. & Kirschner, M. W. Geminin, an inhibitor of DNA replication, is degraded during mitosis. Cell 93, 1043–1053 (1998).

    Article  CAS  PubMed  Google Scholar 

  29. Sakaue-Sawano, A. et al. Visualizing spatiotemporal dynamics of multicellular cell-cycle progression. Cell 132, 487–498 (2008).

    Article  CAS  PubMed  Google Scholar 

  30. Kafri, R. et al. Dynamics extracted from fixed cells reveal feedback linking cell growth to cell cycle. Nature 494, 480–483 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  31. Gut, G., Tadmor, M. D., Pe’er, D., Pelkmans, L. & Liberali, P. Trajectories of cell-cycle progression from fixed cell populations. Nat. Methods 12, 951–954 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  32. Cannoodt, R. et al. SCORPIUS improves trajectory inference and identifies novel modules in dendritic cell development. bioRxiv https://doi.org/10.1101/079509 (2016).

  33. Setty, M. et al. Characterization of cell fate probabilities in single-cell data with Palantir. Nat. Biotechnol. 37, 451–460 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  34. Liang, S., Wang, F., Han, J. & Chen, K. Latent periodic process inference from single-cell RNA-seq data. Nat. Commun. 11, 1441 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  35. Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 32, 381–386 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  36. Takasaki, Y., Deng, J. S. & Tan, E. M. A nuclear antigen associated with cell proliferation and blast transformation. J. Exp. Med. 154, 1899–1909 (1981).

    Article  CAS  PubMed  Google Scholar 

  37. Bravo, R., Frank, R., Blundell, P. A. & Macdonald-Bravo, H. Cyclin/PCNA is the auxiliary protein of DNA polymerase-delta. Nature 326, 515–517 (1987).

    Article  CAS  PubMed  Google Scholar 

  38. Chong, J. P., Mahbubani, H. M., Khoo, C. Y. & Blow, J. J. Purification of an MCM-containing complex as a component of the DNA replication licensing system. Nature 375, 418–421 (1995).

    Article  CAS  PubMed  Google Scholar 

  39. Madine, M. A., Khoo, C. Y., Mills, A. D. & Laskey, R. A. MCM3 complex required for cell cycle regulation of DNA replication in vertebrate cells. Nature 375, 421–424 (1995).

    Article  CAS  PubMed  Google Scholar 

  40. Cayrol, C., Knibiehler, M. & Ducommun, B. p21 binding to PCNA causes G1 and G2 cell cycle arrest in p53-deficient cells. Oncogene 16, 311–320 (1998).

    Article  CAS  PubMed  Google Scholar 

  41. Sherr, C. J. & Roberts, J. M. CDK inhibitors: positive and negative regulators of G1-phase progression. Genes Dev. 13, 1501–1512 (1999).

    Article  CAS  PubMed  Google Scholar 

  42. Viale, G. et al. Prognostic and predictive value of centrally reviewed Ki-67 labeling index in postmenopausal women with endocrine-responsive breast cancer: results from Breast International Group Trial 1-98 comparing adjuvant tamoxifen with letrozole. J. Clin. Oncol. 26, 5569–5575 (2008).

    Article  PubMed  PubMed Central  Google Scholar 

  43. Allegra, C. J. et al. Prognostic value of thymidylate synthase, Ki-67, and p53 in patients with Dukes’ B and C colon cancer: a National Cancer Institute–National Surgical Adjuvant Breast and Bowel Project collaborative study. J. Clin. Oncol. 21, 241–250 (2003).

    Article  CAS  PubMed  Google Scholar 

  44. DeSantis, C. E. et al. Breast cancer statistics, 2019. CA Cancer J. Clin. 69, 438–451 (2019).

    Article  PubMed  Google Scholar 

  45. Rakha, E. A. et al. Breast cancer prognostic classification in the molecular era: the role of histological grade. Breast Cancer Res. 12, 207 (2010).

    Article  PubMed  PubMed Central  Google Scholar 

  46. Allred, D. C. et al. Association of p53 protein expression with tumor cell proliferation rate and clinical outcome in node-negative breast cancer. J. Natl Cancer Inst. 85, 200–206 (1993).

    Article  CAS  PubMed  Google Scholar 

  47. Tannock, I. F. The relation between cell proliferation and the vascular system in a transplanted mouse mammary tumour. Br. J. Cancer 22, 258–273 (1968).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  48. Zaidi, M., Fu, F., Cojocari, D., McKee, T. D. & Wouters, B. G. Quantitative visualization of hypoxia and proliferation gradients within histological tissue sections. Front. Bioeng. Biotechnol 7, 397 (2019).

    Article  PubMed  PubMed Central  Google Scholar 

  49. Muthuswamy, S. K. Self-organization in cancer: implications for histopathology, cancer cell biology, and metastasis. Cancer Cell 39, 443–446 (2021).

    Article  CAS  PubMed  Google Scholar 

  50. Arata, Y. & Takagi, H. Quantitative studies for cell-division cycle control. Front Physiol. 10, 1022 (2019).

    Article  PubMed  PubMed Central  Google Scholar 

  51. Lin, J.-R., Fallahi-Sichani, M. & Sorger, P. K. Highly multiplexed imaging of single cells using a high-throughput cyclic immunofluorescence method. Nat. Commun. 6, 8390 (2015).

    Article  CAS  PubMed  Google Scholar 

  52. Álvarez-Fernández, M. & Malumbres, M. Mechanisms of sensitivity and resistance to CDK4/6 inhibition. Cancer Cell 37, 514–529 (2020).

    Article  PubMed  Google Scholar 

  53. Hafner, M. et al. Multiomics profiling establishes the polypharmacology of FDA-approved CDK4/6 inhibitors and the potential for differential clinical activity. Cell Chem. Biol. 26, 1067–1080.e8 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  54. Moasser, M. M. The oncogene HER2: its signaling and transforming functions and its role in human cancer pathogenesis. Oncogene 26, 6469–6487 (2007).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  55. Goel, S. et al. Overcoming therapeutic resistance in HER2-positive breast cancers with CDK4/6 inhibitors. Cancer Cell 29, 255–269 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  56. Wolff, A. C. et al. Human epidermal growth factor receptor 2 testing in breast cancer: American Society of Clinical Oncology/College of American Pathologists Clinical Practice Guideline Focused Update. J. Clin. Oncol. 36, 2105–2122 (2018).

    Article  CAS  PubMed  Google Scholar 

  57. Slamon, D. J. et al. Human breast cancer: correlation of relapse and survival with amplification of the HER-2/neu oncogene. Science 235, 177–182 (1987).

    Article  CAS  PubMed  Google Scholar 

  58. Filho, O. M. et al. HER2 heterogeneity as a predictor of response to neoadjuvant T-DM1 plus pertuzumab: results from a prospective clinical trial. J. Clin. Oncol. 37, 502–502 (2019).

    Article  Google Scholar 

  59. Katayama, A. et al. Predictors of pathological complete response to neoadjuvant treatment and changes to post-neoadjuvant HER2 status in HER2-positive invasive breast cancer. Mod. Pathol. https://doi.org/10.1038/s41379-021-00738-5 (2021).

  60. Chittajallu, D. R. et al. In vivo cell-cycle profiling in xenograft tumors by quantitative intravital microscopy. Nat. Methods 12, 577–585 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  61. Hanahan, D. & Weinberg, R. A. The hallmarks of cancer. Cell 100, 57–70 (2000).

    Article  CAS  PubMed  Google Scholar 

  62. Moser, J., Miller, I., Carter, D. & Spencer, S. L. Control of the restriction point by Rb and p21. Proc. Natl Acad. Sci. USA 115, E8219–E8227 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  63. Min, M., Rong, Y., Tian, C. & Spencer, S. L. Temporal integration of mitogen history in mother cells controls proliferation of daughter cells. Science 368, 1261–1265 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  64. Amin, A. D., Rajan, S. S., Groysman, M. J., Pongtornpipat, P. & Schatz, J. H. Oncogene overdose: too much of a bad thing for oncogene-addicted cancer cells. Biomark. Cancer 7, 25–32 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  65. Briscoe, J. & Small, S. Morphogen rules: design principles of gradient-mediated embryo patterning. Development 142, 3996–4009 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  66. Rajewsky, N. et al. LifeTime and improving European healthcare through cell-based interceptive medicine. Nature 587, 377–386 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  67. HuBMAP Consortium. The human body at cellular resolution: the NIH Human Biomolecular Atlas Program. Nature 574, 187–192 (2019).

    Article  CAS  Google Scholar 

  68. Caswell-Jin, J. L. et al. Clonal replacement and heterogeneity in breast tumors treated with neoadjuvant HER2-targeted therapy. Nat. Commun. 10, 657 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  69. Lomakin, A. et al. Spatial genomics maps the structure, character and evolution of cancer clones. bioRxiv https://doi.org/10.1101/2021.04.16.439912 (2021).

  70. Rueda, O. M. et al. Dynamics of breast-cancer relapse reveal late-recurring ER-positive genomic subgroups. Nature 567, 399–404 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  71. Zahir, N., Sun, R., Gallahan, D., Gatenby, R. A. & Curtis, C. Characterizing the ecological and evolutionary dynamics of cancer. Nat. Genet. 52, 759–767 (2020).

    Article  CAS  PubMed  Google Scholar 

  72. Hoffer, J. et al. Minerva: a light-weight, narrative image browser for multiplexed tissue images. J. Open Source Softw. 5, 2579 (2020).

    Article  PubMed  PubMed Central  Google Scholar 

  73. Rashid, R. et al. Narrative online guides for the interpretation of digital-pathology images and tissue-atlas data. Nat. Biomed. Eng. https://doi.org/10.1038/s41551-021-00789-8 (2021).

  74. Gaglia, G. et al. Temporal and spatial topography of cell proliferation in cancer. Nat. Cell Biol. https://doi.org/10.7303/syn22300771 (2022).

  75. Mills, C. E. et al. Multiplexed and reproducible high content screening of live and fixed cells using the Dye Drop method. bioRxiv https://doi.org/10.1101/2021.08.27.457854 (2021).

  76. Du, Z. et al. Qualifying antibodies for image-based immune profiling and multiplexed tissue imaging. Nat. Protoc. 14, 2900–2930 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  77. Peng, T. et al. A BaSiC tool for background and shading correction of optical microscopy images. Nat. Commun. 8, 14836 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  78. Muhlich, J., Chen, Y.-A., Russell, D. & Sorger, P. K. Stitching and registering highly multiplexed whole slide images of tissues and tumors using ASHLAR software. bioRxiv https://doi.org/10.1101/2021.04.20.440625 (2021).

  79. Berg, S. et al. ilastik: interactive machine learning for (bio)image analysis. Nat. Methods 16, 1226–1232 (2019).

    Article  CAS  PubMed  Google Scholar 

  80. Creed, J. H., Gerke, T. A. & Berglund, A. E. MatSurv: survival analysis and visualization in MATLAB. J. Open Source Softw. 5, 1830 (2020).

    Article  Google Scholar 

  81. Csikász-Nagy, A., Battogtokh, D., Chen, K. C., Novák, B. & Tyson, J. J. Analysis of a generic model of eukaryotic cell-cycle regulation. Biophys. J. 90, 4361–4379 (2006).

    Article  PubMed  PubMed Central  Google Scholar 

Download references

Acknowledgements

This work was supported by NIH grants R01-CA194005 (S.S.), R41-CA224503 (P.K.S.), U54-CA225088 (P.K.S. and S.S.), P50-CA168504 (J.J.Z. and E.P.W.), R35-CA210057 (J.J.Z.), T32-GM007748 (S.C.), K08-CA191058 (R.J.) and T32-HL007627 (G.G.); DF/HCC Breast SPORE: Specialized Program of Research Excellence (SPORE), the Ludwig Center at Harvard (P.K.S. and S.S.), the American-Italian Cancer Foundation postdoctoral fellowship (G.G.), the Terri Brodeur Breast Cancer Foundation and BCRF-AACR Career Development Awards for Translational Breast Cancer Research (S.K.), the Breast Cancer Research Foundation BCRF (J.J.Z.), DOD CDMRP W81XWH-18-1-0491 (J.J.Z.), the Gray Foundation, and the BWH President’s Scholar Award (S.S.). We thank Dana-Farber/Harvard Cancer Center for the use of the Specialized Histopathology Core, which provided histopathology services. Dana-Farber/Harvard Cancer Center is supported in part by a National Cancer Institute (NCI) Cancer Center Support Grant P30-CA06516. Tissue samples were also provided by the Cooperative Human Tissue Network (CHTN), which is funded by the NCI. Other investigators may have received specimens from the same subjects. We thank C. Yapp and Y.-A. Chen for assistance with microscopy and image analysis, and C. Rycroft and G. Lahav for helpful discussions.

Author information

Author notes

  1. These authors contributed equally to this work: Giorgio Gaglia, Sheheryar Kabraji.

Authors and Affiliations

  1. Laboratory of Systems Pharmacology, Department of Systems Biology, Harvard Medical School, Boston, MA, USA

    Giorgio Gaglia, Sheheryar Kabraji, Danae Rammos, Yang Dai, Ana Verma, Shu Wang, Caitlin E. Mills, Mirra Chung, Shannon Coy, Jia-Ren Lin, Peter K. Sorger & Sandro Santagata

  2. Ludwig Center at Harvard, Harvard Medical School, Boston, MA, USA

    Giorgio Gaglia, Sheheryar Kabraji, Danae Rammos, Yang Dai, Ana Verma, Shannon Coy, Jia-Ren Lin, Peter K. Sorger & Sandro Santagata

  3. Department of Pathology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA

    Giorgio Gaglia, Danae Rammos, Yang Dai, Ana Verma, Shannon Coy, Deborah A. Dillon & Sandro Santagata

  4. Department of Medical Oncology, Dana Farber Cancer Institute, Boston, MA, USA

    Sheheryar Kabraji, Rinath Jeselsohn, Otto Metzger & Eric P. Winer

  5. Department of Cancer Biology, Dana Farber Cancer Institute, Boston, MA, USA

    Sheheryar Kabraji, Johann S. Bergholz & Jean J. Zhao

  6. Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA

    Sheheryar Kabraji & Rinath Jeselsohn

  7. Harvard Graduate Program in Biophysics, Harvard University, Cambridge, MA, USA

    Shu Wang

  8. Department of Pathology, Dana Farber Cancer Institute, Boston, MA, USA

    Sandro Santagata

Authors
  1. Giorgio Gaglia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sheheryar Kabraji
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Danae Rammos
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yang Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ana Verma
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Shu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Caitlin E. Mills
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Mirra Chung
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Johann S. Bergholz
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Shannon Coy
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Jia-Ren Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Rinath Jeselsohn
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Otto Metzger
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Eric P. Winer
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Deborah A. Dillon
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Jean J. Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Peter K. Sorger
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Sandro Santagata
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

G.G., S.K., J.J.Z., P.K.S. and S.S. were responsible for study conceptualization. G.G., S.K., S.W., C.E.M., J.B., S.C., J.R.L., P.K.S. and S.S. developed and implemented the methodology. G.G., S.K., D.R., Y.D., A.V., C.E.M., .M.C. and S.C. conducted data acquisition. G.G., D.R. and Y.D. generated software. G.G., S.K., D.R., Y.D., S.C., D.A.D. and D.R. performed data validation. G.G., S.K., D.R., Y.D., A.V., C.E.M. and S.C. performed formal analysis. J.B., D.A.D., R.J., O.M. and E.P.W. provided resources. G.G., S.K., D.R., Y.D., S.C. and D.A.D. performed data curation. G.G., S.K. and S.S. wrote the original draft, and all authors reviewed and edited the manuscript. Data visualization was conducted by G.G., S.K., Y.D. and D.R. J.J.Z., P.K.S. and S.S. provided project supervision, and P.K.S. and S.S. provided project administration. E.P.W., J.J.Z., P.K.S. and S.S. provided resources and funding.

Corresponding authors

Correspondence to Sheheryar Kabraji or Sandro Santagata.

Ethics declarations

Competing interests

P.K.S. is a member of the Scientific Advisory Board of RareCyte and NanoString Technologies, is on the Board of Directors of Applied Biomath and is a consultant to Merck and Montai Health. P.K.S. is co-founder of Glencoe Software, which contributes to and supports the open-source OME/OMERO image informatics software used in this paper. S.S. is a consultant for RareCyte, and J.J.Z. is a founder and board director of Crimson Biotech and Geode Therapeutics. J.S.B. is a scientific consultant and has stock options for Geode Therapeutics. D.A.D. is on the Advisory Board for Oncology Analytics and has consulted for Novartis. The other authors declare no competing interests.

Peer review

Peer review information

Nature Cell Biology thanks Tobias Meyer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Multivariate Proliferation Index (MPI) in human cancer tissues.

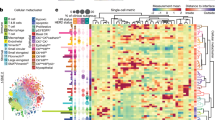
a. Clustered heat map of log2 normalized cell lineage marker signal intensities on a per-cell basis derived from CyCIF images of 4 whole slides of lung squamous cell carcinoma (SCC) and ovarian carcinoma, and tissue microarrays (TMAs) from glioma, colorectal carcinoma (CRC) and mesothelioma. b-c. Clustered heat map of single-cell signal intensities of cell cycle markers for epithelial/tumour cells in Fig. 1a (breast carcinoma) and panel a. Ki-67+ cells were identified by normalization using Gaussian mixture modeling with 2 components. Multivariate Proliferation Index (MPI) indicated: +1 (proliferative, green), 0 (non-proliferative, blue), or -1 (arrested, red). d. K-means clustering heat map of five MPI markers for epithelial/tumour cells of three HER2 + breast cancer samples (k = 20 clusters), and heat map of single-cell normalized log2 intensities. In both, the corresponding MPI category is depicted for comparison (k-mean clustering fraction of MPI category is depicted). e. UMAP plots for 180 samples of breast carcinomas from the Cooperative Human Tissue Network (CHTN) Stage II TMAs (#14-17) with proliferation markers mapped to colour (MPI categories were not used as UMAP variables, n = 10,000 cells). f. MPI robustness comparison between five sets of serially cut tissue sections from Pantomics TMA BRC15010 and g. between two sets of serially cut tissue sections of the 3 breast HER2-positive cases from Fig. 1c,e. Each dot represents the fraction of MPI + 1 cells in the two indicated tissue sections (linear least-square fit with fixed origin at y = x = 0). h-j. Permutation testing of breast carcinomas from the CHTN Stage II TMAs (#14-17, n = 180 samples) with MPI calculations performed by adding increasing amounts of normally distributed noise (0.1x, 0.25x, 0.5x and 1x standard deviations of original marker distribution) to the five MPI cutoffs, repeated 1000 times using i. linear regression, i. correlation analysis (boxplots: median, 25-75th percentile and min-max extremes from MatLab boxplot.m function), and j. intra-cohort ordering of MPI estimates. k. Comparison of MPI 0, and MPI -1 fractions in epithelial/tumour cells across different classifiers of breast cancer in Fig. 1g (n = 142 samples, mean + SD, 2-sided KS p-values with 0.05 significance cutoff).

Extended Data Fig. 2 Multivariate Proliferation Index (MPI) short- and long-range correlations in human cancer tissues.

a-b. Composite CyCIF image from a. lung squamous cell carcinoma, and b. ovarian carcinoma (scale bar, 1 mm) and corresponding image of long-range whole slide spatial maps of MPI categories (smoothed over 40 neighbouring cells for visualization purposes only). Inset panel showing both smoothed and single-cell MPI calling in marked region of interest. Further inset panel of single-cell MPI calling and corresponding composite CyCIF image (scale bar, 100 µm; white = pan-cytokeratin, green = MCM2, red = p27, blue = DNA; example from 4 biological independent specimens). c. Spatial maps of MPI categories from inset 1 from Fig. 2a smoothed over 40 neighbouring cells and non-smoothed (single-cell calling). d. Red density curve shows sample distribution of spatial correlations within and across (“self corr” and “cross corr”) MPI categories for mesothelioma, glioma, colorectal carcinoma (CRC) and three breast TMAs (n = 52, 163, 89, 69, 85, 57 samples respectively, k = 5th neighbour approximation, kernel smoothing (KS) density approximation). Blue density curve shows bootstrap distribution comparison obtained by randomly shuffling of MPI labels (10 independent shuffles). e. Heat map of spatial correlations within and across randomly shuffled MPI labels (“self corr” and “cross corr”, k = 5th neighbour, n = 513 samples). f. 2-sided t-test p-values for red density curve distributions in panel d (log10 scale used for visualization purposes). g. Plots of spatial correlation from whole slides images of samples in Fig. 2d with two exponential fit for the three MPI categories. h. Ripley’s L-r function for MPI + 1 across breast, lung, and ovarian tumours (whole slide images, Fig. 2d). Each column represents an individual and independent tissue.

Extended Data Fig. 3 Limits of cell cycle marker single cell distributions and multi-channel gating interpretation in tissues.

a. Representative single-channel cell cycle marker images from CyCIF imaging with E-cadherin from tissue in Fig. 3a (scale bar 100 µm, example from 3 biological independent specimens). b. Single-channel distributions and two-dimensional scatter plots of a subset of cell cycle markers from HER2 positive breast cancer case #2 in Fig. 1c,e (n = 1,000 epithelial/tumour cells, log2 signal per cell prior to normalization). c. Single channel distributions for cell lineage, proliferation, and cell cycle markers from three HER2 + breast cancer samples (kernel smoothing (KS) density approximation) used in Fig. 1c,e. For proliferation and cell cycle markers only epithelial/tumour cells were used. d. Upset plot of three HER2 + breast cancer samples (n = 0.52 million cells) from Fig. 1c, e showing frequency of cell cycle marker positivity and their combinations sorted by frequency.

Extended Data Fig. 4 Example of 27-plex CyCIF experiment with tumour sample and tonsil control tissues.

a. Example of positive and negative staining for all markers in CyCIF experiment through rounds of cyclic imaging. Three independent samples are shown: Ctrl is a non-malignant tonsil tissue sample (‘control’), #1 and #2 are glioma samples. Plots are single-cell kernel smoothing (KS) density estimation for patient samples from respective images (median per pixels within the cell area, log2 FAU, not normalized, black = tonsil, yellow = glioma sample #1, magenta = glioma sample #2, n = 4,278, 2,629, and 2,609 cells, respectively). Each row of images and data is a successive round of CyCIF acquired from the same tissue area (Rx is the xth round of imaging). All images from antibody channels were linearly contrasted between 0 and 2000 fluorescence units for ease of comparison. Scale bar, 50 µm. Examples from tissue microarray containing 176 independent glioma specimens and 8 independent control specimens. b. Scatter plots of the single-cell correlation of the signal intensity of unconjugated antibodies to the indicated markers versus their fluorophore conjugated versions from 142 samples of tissue from 75 patients (Pantomics TMA BRC15010). Pearson correlation coefficients (C) are shown. All correlation had p-value < 10-175. c. Plot of the phospho-Rb signal from MPI0, MPI + 1/Ki-67-, and MPI + 1/Ki-67+ cells from Pantomics TMA BRC15010 acquired using both conjugated (‘direct IF’) and unconjugated (‘indirect IF’) phospho-Rb antibodies (n = 74 cores, Line is mean value).

Extended Data Fig. 5 Testing of ccD-CMD framework using cell cycle perturbation in vitro and cell cycle modeling in silico, and comparison of temporal inference methods.

a. Left, histograms of fluorescence single-cell log2 normalized signal by plate-based CyCIF (p-CyCIF) from untreated (blue) and 24 h palbociclib 1 µM treated (orange) MCF10A cells grown in culture (n = 10,000 cells per condition). Right, ccD-CMD plot. b. Heat map and time plot of single-cell signals ordered by ccD-CMD (normalized log2 FAU, n = 10,000 cells moving mean over 200 cells). c. Traces from generalized model of mammalian cell cycle80. Top panels, no noise added. Middle panels, Gaussian measurement noise added (additive and multiplicative). Gray areas are the time frame used for plots in panels d. d. ccD-CMD plot of mathematical model results in shaded areas of panel c. Bottom panel, simulation switch to G1 arrest parameters (CDK/CyclinD complex set to 0) after one cell cycle. Colour is the time variable in the mathematical model (n = 10,000 points). e-h. Comparison of time inference methods ccD-CMD, SCORPIUS, Palantir and Cyclum applied to e. synthetic data generated by the mathematical model in panel e. (n = 10,000 observations), f. HER2 + breast cancer tissue data from Fig. 3a-f., and g. MCF10A untreated cells from Fig. 3g. Left, two dimensional visualization output. Right, pseudotime ordering output (n = 5,000 cells, same cells used for all algorithms, normalized log2 FAU, moving mean over 200 cells). h. Comparison between two dimensional reduced space visualization from three time inference algorithms with data from HER2 + breast patient samples #1, 2, and 3 from Fig. 4b-d. i. Coefficient of variation of coherence metrics IOV and CFD in 5 tissues using increasing number of cells (n > 20,000 cells per tissue, CV calculated over 40 independent sub-samplings). j. Comparison of IOV and CFD when one or two markers are removed from ccD-CMD algorithm. Data from untreated MCF10A cells used in panel g. The green dot is the original representation. Orange, one marker removed. Blue, two markers removed. k. Comparison of IOV and CFD when MPI 0 and MPI -1 cells are added at increasing ratios. l. Examples of pseudotime ordering by ccD-CMD algorithm showing inferred CDT1 and Geminin across six tissues areas.

Extended Data Fig. 6 Orthogonal validation of changes in MPI and cell cycle coherence using cell cycle inhibition in vitro and in vivo.

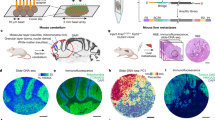
a-b. Stacked bar graphs showing a. cell cycle fractions using the dye drop method75 and b. MPI frequencies by p-CyCIF for MCF-7 cells at baseline and in response indicated treatments for 24 h c. Cell cycle fractions in five breast cancer cell lines showing differential response to treatment with increasing doses of Palbociclib dependent on the Rb status of the cell line. d. ccD-CMD plot from p-CyCIF from fixed untreated cells (Control), and cells exposed to 1 µM Palbociclib for 24 h. Enlarged dot represents the average of 3 distinct biological replicates, n = 1000 cells each. e-g. t-CyCIF validation in MCF-7 xenografts in nude mice53. Doses are in mg/kg. e. Scatter plot of change in tumour size and MPI + 1 fraction. Vehicle, n = 14 tumours from 7 mice. Abemaciclib, n = 6 tumours from 3 mice per dose. Palbociclib, n = 8 tumours from 5 mice. Each dot represents an individual tumour (2-sided Pearson correlation p-value). f. MPI and Ki-67 fractions per TMA core (mean of n = 35, 15, 17, 18, and 24 total cores, 2-sided t-test p-value). g. ccD-CMD plots from individual MCF-7 xenografts tumours (4000 cells per mouse, n = 12, 6, 6, 6, 8 mice).

Extended Data Fig. 7 Cell cycle dynamics from ccD-CMD from human cancer tissues.

a. Scatter plot of CFD versus IOV (for each ROI from Fig. 4f). b. K-means clustering of cell cycle markers from selected ROIs used in Fig. 4g (n = 3600 cells per ROI, k = 15 clusters). Left, single-cell clustering with ROI annotation (log2 normalized FAU). Middle, cluster median. Right, ROI composition for each cluster. c. Scanned image of hematoxylin and eosin (H&E) stained section from three HER2 positive breast tissues with pathology annotations. d. Composite CyCIF images of tissues from panel c (green CD45, red Vimentin, white E-Cadherin, scale bar 2 mm). e. Inter-Octile Variation IOV, f. Circle Fit Distance (CFD), and g. MPI + 1 fraction for each ROI noted in panel d.

Extended Data Fig. 8 HER2 expression and cell cycle dynamics in human breast cancer tissues and HER2 driven mouse model of breast cancer.

a. ccD-CMD plots for two HER2 + breast cancer tissue microarrays (TMA # 1 and #2) for increasing levels for HER2 protein. Single cells binned by normalized HER2 levels (n = 5,000 cells per bin were used). Right, ccD-CMD scatter plots of highest HER2 bin for both TMA1 and 2 with single marker normalized intensities mapped to colour (n = 5,000 cells). b. ccD-CMD scatter plots of the single-cell data from MPI + 1 cells from time course of HER2 induction and repression in GEMM with single marker normalized intensities mapped to colour (n = 5,000 cells per plot, p27 was not used by the ccD-CMD algorithm). c. Mean + /- 25th percentile of circle fit distance of cell cycle markers in tumour cells (in situ and invasive) from Fig. 5h (n = 5,000 cells per plot).

Extended Data Fig. 9 Association between with clinical outcome and cell proliferation metrics.

a. Scatter plots of CFD versus IOV from mesothelioma and glioblastoma sample cohorts (n = 22 and 32 patients, respectively). Colors represent binning into coherence groups according IOV and CFD metrics. b-c. Kaplan Meier estimation and logrank p-value of progression-free survival (PFS) for the two patient cohorts in Fig. 7. Patients were binned in b. three groups “coherent”, IOVhigh “skewed” and IOVlow CFDhigh “non-canonical” groups from panel a). or c. two groups based on the median Ki-67+ fraction.

Supplementary information

Supplementary Information

Supplementary Note/Discussion

Reporting Summary

Peer Review Information

Supplementary Table 1

This file contains Supplementary Tables 1–8 as outlined in the main text.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gaglia, G., Kabraji, S., Rammos, D. et al. Temporal and spatial topography of cell proliferation in cancer. Nat Cell Biol 24, 316–326 (2022). https://doi.org/10.1038/s41556-022-00860-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41556-022-00860-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing: Cancer

Sign up for the Nature Briefing: Cancer newsletter — what matters in cancer research, free to your inbox weekly.

Get what matters in cancer research, free to your inbox weekly. Sign up for Nature Briefing: Cancer