Abstract
When the light from a distant object passes very near to a foreground galaxy or cluster, gravitational lensing can cause it to appear as multiple images on the sky1. If the source is variable, it can be used to constrain the cosmic expansion rate2 and dark energy models3. Achieving these cosmological goals requires many lensed transients with precise time-delay measurements4. Lensed supernovae are attractive for this purpose because they have relatively simple photometric behaviour, with well-understood light curve shapes and colours—in contrast to the stochastic variation of quasars. Here we report the discovery of a multiply imaged supernova, AT 2016jka (‘SN Requiem’). It appeared in an evolved galaxy at redshift 1.95, gravitationally lensed by a foreground galaxy cluster5. It is probably a type Ia supernova—the explosion of a low-mass stellar remnant, whose light curve can be used to measure cosmic distances. In archival Hubble Space Telescope imaging, three lensed images of the supernova are detected with relative time delays of <200 d. We predict that a fourth image will appear close to the cluster core in the year 2037 ± 2. Observation of the fourth image could provide a time-delay precision of ~7 d, <1% of the extraordinary 20 yr baseline. The supernova classification and the predicted reappearance time could be improved with further lens modelling and a comprehensive analysis of systematic uncertainties.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
All HST images used in this work are available from the Mikulski Archive for Space Telescopes (mast.stsci.edu). HST data from 2016 when the transient was active are from the programme HST-GO-14496 (archive.stsci.edu/proposal_search.php?id=14496&mission=hst). Data collected in 2019 are from the REQUIEM programme, HST-GO-15663 (archive.stsci.edu/proposal_search.php?id=15663&mission=hst). All VLT/MUSE spectroscopic data used in this work are available from the ESO Archive Science Portal (archive.eso.org/dataset/ADP.2019-10-07T18:14:24.762, archive.eso.org/dataset/ADP.2019-10-07T18:14:24.751 and archive.eso.org/dataset/ADP.2019-10-07T18:14:24.776). All derived data supporting the findings of this study (photometry, lens model inputs and so on) are available within this Letter and Supplementary Information. Source data are provided with this paper.
Code availability
All software tools used in the analysis are publicly available, as indicated in the text. The software used for figure creation, including input data files, can be downloaded from github.com/gbrammer/mrg0138_supernova.
References
Einstein, A. Lens-like action of a star by the deviation of light in the gravitational field. Science 84, 506–507 (1936).
Refsdal, S. On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon. Not. R. Astron. Soc. 128, 307–310 (1964).
Holz, D. E. Seeing double: strong gravitational lensing of high-redshift supernovae. Astrophys. J. 556, L71–L74 (2001).
Treu, T. & Marshall, P. J. Time delay cosmography. Astron. Astrophys. Rev. 24, 11 (2016).
Brammer, G. et al. Discovery of Probable Multiply Imaged Supernova in Archival HST Data Transient Discovery Report 113893 (Transient Name Server, 2021).
Akhshik, M. et al. Recent star formation in a massive slowly quenched lensed quiescent galaxy at z = 1.88. Astrophys. J. Lett. 907, L8 (2021).
Newman, A. B., Belli, S., Ellis, R. S. & Patel, S. G. Resolving quiescent galaxies at z > 2. II. Direct measures of rotational support. Astrophys. J. 862, 126 (2018).
Ebeling, H., Edge, A. C. & Henry, J. P. MACS: a quest for the most massive galaxy clusters in the universe. Astrophys. J. 553, 668–676 (2001).
Jullo, E. et al. A Bayesian approach to strong lensing modelling of galaxy clusters. New J. Phys. 9, 447–447 (2007).
Kneib, J.-P. et al. LENSTOOL: a gravitational lensing software for modeling mass distribution of galaxies and clusters (strong and weak regime). Astrophysics Source Code Library ascl:1102.004 (2011).
Kasen, D. & Woosley, S. E. On the origin of the type Ia supernova width–luminosity relation. Astrophys. J. 656, 661–665 (2007).
Riess, A. G. et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116, 1009–1038 (1998).
Perlmutter, S. et al. Measurements of ω and λ from 42 high-redshift supernovae. Astrophys. J. 517, 565–586 (1999).
Riess, A. G., Casertano, S., Yuan, W., Macri, L. M. & Scolnic, D. Large Magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 876, 85 (2019).
Planck Collaboration et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020).
Verde, L., Treu, T. & Riess, A. G. Tensions between the early and late Universe. Nat. Astron. 3, 891–895 (2019).
Birrer, S. et al. TDCOSMO. IV. Hierarchical time-delay cosmography—joint inference of the Hubble constant and galaxy density profiles. Astron. Astrophys. 643, A165 (2020).
Birrer, S. & Treu, T. TDCOSMO. V. Strategies for precise and accurate measurements of the Hubble constant with strong lensing. Astron. Astrophys. 649, A61 (2021).
Spergel, D. et al. Wide-Field Infrared Survey Telescope–Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 report. Preprint at https://arxiv.org/abs/1503.03757 (2015).
Ivezic, Z. et al. LSST: from science drivers to reference design and anticipated data products. Astrophys. J. 873, 111 (2019).
Kelly, P. L. et al. Multiple images of a highly magnified supernova formed by an early-type cluster galaxy lens. Science 347, 1123–1126 (2015).
Kelly, P. L. et al. Déjà vu all over again: the reappearance of supernova Refsdal. Astrophys. J. 819, L8 (2016).
Goobar, A. et al. iPTF16geu: a multiply imaged, gravitationally lensed type Ia supernova. Science 356, 291–295 (2017).
Dhawan, S. et al. Magnification, dust and time-delay constraints from the first resolved strongly lensed type Ia supernova iPTF16geu. Mon. Not. R. Astron. Soc. 491, 2639–2654 (2020).
Quimby, R. M. et al. Detection of the gravitational lens magnifying a type Ia supernova. Science 344, 396–399 (2014).
Goldstein, D. A., Nugent, P. E. & Goobar, A. Rates and properties of supernovae strongly gravitationally lensed by elliptical galaxies in time-domain imaging surveys. Astrophys. J. Suppl. Ser. 243, 6 (2019).
Pierel, J. D. R. et al. Projected cosmological constraints from strongly lensed supernovae with the Roman Space Telescope. Astrophys. J. 908, 190–207 (2021).
Rodney, S. A. et al. SN Refsdal: photometry and time delay measurements of the first Einstein cross supernova. Astrophys. J. 820, 50 (2016).
Millon, M. et al. COSMOGRAIL. XIX. Time delays in 18 strongly lensed quasars from 15 years of optical monitoring. Astron. Astrophys. 640, A105 (2020).
Millon, M. et al. TDCOSMO. II. Six new time delays in lensed quasars from high-cadence monitoring at the MPIA 2.2 m telescope. Astron. Astrophys. 642, A193 (2020).
Gonzaga, S. et al. The DrizzlePac Handbook (Space Telescope Science Institute, 2012).
Astropy Collaboration et al. The Astropy Project: building an open-science project and status of the v2.0 core package. Astron. J. 156, 123 (2018).
Weilbacher, P. M. et al. The data processing pipeline for the MUSE instrument. Astron. Astrophys. 641, A28 (2020).
Bacon, R. et al. The MUSE Hubble Ultra Deep Field Survey: I. Survey description, data reduction, and source detection. Astron. Astrophys. 608, A1 (2017).
Richard, J. et al. An atlas of MUSE observations towards twelve massive lensing clusters. Astron. Astrophys. 646, A83 (2021).
Soto, K. T., Lilly, S. J., Bacon, R., Richard, J. & Conseil, S. ZAP—enhanced PCA sky subtraction for integral field spectroscopy. Mon. Not. R. Astron. Soc. 458, 3210–3220 (2016).
iqueras, L. et al. MPDAF—a Python package for the analysis of VLT/MUSE data. In Astronomical Data Analysis Software and Systems XXVI: Astronomical Society of the Pacific Conference Series Vol. 521 (eds Molinaro, M. et al.) 545 (Astronomical Society of the Pacific, 2019).
Mahler, G. et al. Strong-lensing analysis of A2744 with MUSE and Hubble Frontier Fields images. Mon. Not. R. Astron. Soc. 473, 663–692 (2018).
Lagattuta, D. J. et al. Probing 3D structure with a large MUSE mosaic: extending the mass model of Frontier Field Abell 370. Mon. Not. R. Astron. Soc. 485, 3738–3760 (2019).
Richard, J. et al. Mass and magnification maps for the Hubble Space Telescope Frontier Fields clusters: implications for high-redshift studies. Mon. Not. R. Astron. Soc. 444, 268–289 (2014).
Richard, J. et al. LoCuSS: first results from strong-lensing analysis of 20 massive galaxy clusters at z = 0.2. Mon. Not. R. Astron. Soc. 404, 325–349 (2010).
Mannucci, F. et al. The supernova rate per unit mass. Astron. Astrophys. 433, 807–814 (2005).
Newman, A. B., Belli, S., Ellis, R. S. & Patel, S. G. Resolving quiescent galaxies at z > 2. I. Search for gravitationally lensed sources and characterization of their structure, stellar populations, and line emission. Astrophys. J. 862, 125 (2018).
Foley, R. J. & Mandel, K. Classifying supernovae using only galaxy data. Astrophys. J. 778, 167 (2013).
Smartt, S. J. Progenitors of core-collapse supernovae. Annu. Rev. Astron. Astrophys. 47, 63–106 (2009).
Li, X., Hjorth, J. & Richard, J. The rates and time-delay distribution of multiply imaged supernovae behind lensing clusters. J. Cosmol. Astropart. Phys. 2012, 015 (2012).
Barbary, K. et al. sncosmo/sncosmo: v1.4.0. Zenodo https://doi.org/10.5281/zenodo.168220 (2016).
Rodney, S. A. et al. Type Ia supernova rate measurements to redshift 2.5 from CANDELS: searching for prompt explosions in the early universe. Astron. J. 148, 13 (2014).
Guy, J. et al. SALT2: using distant supernovae to improve the use of type Ia supernovae as distance indicators. Astron. Astrophys. 466, 11–21 (2007).
Pierel, J. D. R. et al. Extending supernova spectral templates for next-generation space telescope observations. Publ. Astron. Soc. Pac. 130, 114504 (2018).
Kessler, R. et al. SNANA: a public software package for supernova analysis. Publ. Astron. Soc. Pac. 121, 1028–1035 (2009).
Frieman, J. A. et al. The Sloan Digital Sky Survey—II Supernova Survey: technical summary. Astron. J. 135, 338–347 (2008).
Sako, M. et al. The Sloan Digital Sky Survey—II Supernova Survey: search algorithm and follow-up observations. Astron. J. 135, 348–373 (2008).
D’Andrea, C. B. et al. Type II-P supernovae from the SDSS-II Supernova Survey and the Standardized Candle Method. Astrophys. J. 708, 661–674 (2010).
Astier, P. et al. The Supernova Legacy Survey: measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 447, 31–48 (2006).
Hamuy, M. et al. The Carnegie Supernova Project: the low-redshift survey. Publ. Astron. Soc. Pac. 118, 2–20 (2006).
Stritzinger, M. et al. The He-rich core-collapse supernova 2007Y: observations from x-ray to radio wavelengths. Astrophys. J. 696, 713–728 (2009).
Morrell, N. I. Carnegie Supernova Project: spectroscopic observations of core collapse supernovae. In Death of Massive Stars: Supernovae and Gamma-Ray Bursts: IAU Symposium Vol. 279 (eds Roming, P. et al.) 361–362 (IAU, 2012).
Skilling, J. Nested sampling. Am. Inst. Phys. Conf. Ser. 735, 395–405 (2004).
Pierel, J. D. R. & Rodney, S. Turning gravitationally lensed supernovae into cosmological probes. Astrophys. J. 876, 107 (2019).
Huber, S. et al. Strongly lensed SNe Ia in the era of LSST: observing cadence for lens discoveries and time-delay measurements. Astron. Astrophys. 631, A161 (2019).
Goldstein, D. A., Nugent, P. E., Kasen, D. N. & Collett, T. E. Precise time delays from strongly gravitationally lensed type Ia supernovae with chromatically microlensed images. Astrophys. J. 855, 22 (2018).
Foxley-Marrable, M., Collett, T. E., Vernardos, G., Goldstein, D. A. & Bacon, D. The impact of microlensing on the standardization of strongly lensed type Ia supernovae. Mon. Not. R. Astron. Soc. 478, 5081–5090 (2018).
Bonvin, V. et al. Impact of the 3D source geometry on time-delay measurements of lensed type-Ia supernovae. Astron. Astrophys. 621, A55 (2019).
Kochanek, C. S. Quantitative interpretation of quasar microlensing light curves. Astrophys. J. 605, 58–77 (2004).
Vernardos, G. A joint microlensing analysis of lensing mass and accretion disc models. Mon. Not. R. Astron. Soc. 480, 4675–4683 (2018).
Hsiao, E. Y. et al. K -corrections and spectral templates of type Ia supernovae. Astrophys. J. 663, 1187–1200 (2007).
Kessler, R. et al. Results from the Supernova Photometric Classification Challenge. Publ. Astron. Soc. Pac. 122, 1415–1431 (2010).
Wang, X., Wang, L., Pain, R., Zhou, X. & Li, Z. Determination of the Hubble constant, the intrinsic scatter of luminosities of type Ia supernovae, and evidence for nonstandard dust in other galaxies. Astrophys. J. 645, 488–505 (2006).
Mosher, J. et al. Cosmological parameter uncertainties from SALT-II type Ia supernova light curve models. Astrophys. J. 793, 16 (2014).
Acknowledgements
We thank P. Kelly and L. Moustakas for helpful commentary on earlier drafts of this work. Data are based on observations made with the NASA/ESA HST, obtained from the data archive at the Space Telescope Science Institute, and on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 0103.A-0777(A). Support for this work was provided by NASA through grant numbers HST-GO-14622 (K.E.W.), HST-AR-15050 (J.D.R.P.), HST-GO-15663 (M.A.) and HST-GO-16264 (S.A.R.) from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc. under NASA contract NAS 5-26555. The Cosmic Dawn Center of Excellence is funded by the Danish National Research Foundation under grant no. 140. Support was provided by NASA Headquarters under the NASA Future Investigators in Earth and Space Science and Technology (FINESST) awards 80NSSC19K1414 (M.A.) and 80NSSC19K1418 (J.D.R.P.). K.E.W. acknowledges funding from the Alfred P. Sloan Foundation.
Author information
Authors and Affiliations
Contributions
Conceptualization, S.A.R., G.B.B. and S.T.; methodology, S.A.R., J.D.R.P., J.R. and K.F.O.; investigation, G.B.B., J.R., S.T., M.A. and K.E.W.; writing—original draft, G.B.B. and S.T.; writing—review and editing, S.A.R., G.B.B., J.D.R.P., J.R., S.T., K.F.O., M.A. and K.E.W.; visualization, S.A.R., G.B.B., J.D.R.P., J.R. and K.F.O.; supervision, S.A.R., G.B.B., S.T. and K.E.W.; funding acquisition, M.A., K.E.W., J.D.R.P. and S.A.R.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Astronomy thanks Ariel Goobar, Anupreeta More and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Elements of the MRG0138 cluster lens model.
The model comprises 37 potentials in total: the BCG (red), 32 cluster members (yellow), three perturbers (cyan), and the main cluster potential (pink). Labeled × symbols indicate the positions of the SN, host, and one additional multiply imaged galaxy with a secure redshift used as model constraints (Supplemental Table 3). The filters used to generate the color image are as in Fig. 1, and tick marks are separated by 10 arcsec.
Extended Data Fig. 2 The position of AT 2016jka in color-magnitude space.
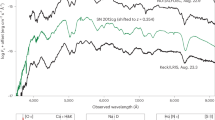
Colored points show simulated photometry for normal SNe of Type Ia (red), Type Ib/Ic (gold), and Type II (green), with 10,000 simulated SNe in each subclass (not all apparent on this plot). Histograms above and below show the marginalized distributions that have been rescaled to represent posterior probability density functions. They are normalized to integrate to unity, then multiplied by the SN subclass priors based on the host galaxy stellar population (row b in Supplementary Table 2). Open markers show the observed photometry of the SN. Dotted vertical lines mark the magnification correction based on the preferred LENSTOOL model (model E, described in Methods: Lens Modeling). Closed markers show the resulting magnification-corrected photometry, with asymmetric error bars reflecting the systematic uncertainty derived from the five lens model variants. Horizontal error bars in the upper panel indicate the observed uncertainty in the SN color (not affected by lensing). The relevant SN photometry markers are repeated in the histogram side-panels with arbitrary vertical positions. All three SN images are located in regions of color-magnitude space that are expected to be dominated by Type Ia SNe.
Extended Data Fig. 3 A representative set of light curve and color curve models from the STARDUST2 classification algorithm.
Panels a-f show F105W and F160W, as indicated, plotting the model light curves in black and photometry as red markers. Panels g-i show the F105W-F160W color curves and color data. All data points as shown have been corrected for magnification and shifted in time using the preferred LENSTOOL model (model E, described in Methods: Lens Modeling). Plotted error bars include the measurement uncertainty and the lens modeling magnification uncertainty. Data points in the right column also include this magnification uncertainty, even though cluster-scale lensing is achromatic, because the STARDUST2 analysis was done on the light curve data, not the color data directly. In all panels the first data point is SN image 2, followed by image 1 and image 3. In each panel the black curves show 200 SN light curve models drawn at random from the nested sampling sequence of the STARDUST2 (sncosmo) classification.
Extended Data Fig. 4 Color-based age constraints for AT 2016jka.
Constraints are shown separately for Image SN1 (panels a and b), image 2 (c and d), and image 3 (e and f), using the methodology described in Methods: Color Curve Age Constraints. Large lower panels (b, d and f) show the observations and model fits. Each magenta shaded region shows the 1σ range of the measured F105W-F160W color, which corresponds to a U-V color in the rest-frame. The model fits are shown as grey shaded regions, indicating the 68% confidence interval of the best-fit SALT2 color curve, with the median model shown as a solid line. The small upper panels (a, c and e) show the posterior for the age of each image from SNTD, using a prior on the SALT2 color parameter (c) based on known population characteristics of SNIa. The effect of adding this prior is slight, with no significant deviation from the best-fit value of \(c = 0.02_{-0.05}^{+0.04}\).
Extended Data Fig. 5 Marginalized and joint posterior distributions for the color curve age constraints measured in this analysis.
Two-dimensional plots show MCMC sampling points as discrete dots, with contours for the high density regions, drawn at 0.5, 1, 1.5 and 2σ levels. Marginalized (1D) distributions are shown at the top of each column, with dashed vertical lines at the mean and ± 1σ (marking 16%, 50% and 84% levels). We use a weak prior on the SALT2 color parameter (c), and set the SALT2 stretch parameter (x1) to 0. This method is fully independent of lens modeling. The table in the upper right lists all priors, observations, and lens model information used for SN age estimates in this work. Only the highlighted components were used for the constraints shown here.
Extended Data Fig. 6 Light-curve-based age constraints for AT 2016jka.
Constraints are shown separately for Image SN1 (panels a and b), image 2 (c and d), and image 3 (e and f), using the methodology described in Methods: Light Curve Age Constraints. Large lower panels (b, d and f) show the observations and model fits. Each orange shaded region shows the 1σ range of the measured F160W magnitude after lens model correction (see Table 1), which corresponds to roughly V band in the rest-frame. The model fits are shown as grey shaded regions, indicating the 68% confidence interval of the best-fit SALT2 light curve, with the median model shown as a solid line. Small upper panels (a, c and e) show the posterior distributions from SNTD for the age of each image that is independent of the lens model (magenta, same as Extended Data Figure 7), using the preferred lens model E (light blue), and the combination of both methods (orange).
Extended Data Fig. 7 Marginalized and joint posterior distributions for the final age constraints measured in this analysis.
Two-dimensional plots show MCMC sampling points as discrete dots, with contours for the high density regions, drawn at 0.5, 1, 1.5 and 2σ levels. Marginalized (1D) distributions are shown at the top of each column, with dashed vertical lines at the mean and ± 1σ (marking 16%, 50% and 84% levels). We use the color curve posterior as the prior for light curve fitting with lens model E, and include weak priors on the absolute magnitude of a SNIa (MB) and the SALT2 color parameter (c), and set the SALT2 stretch parameter (x1) to 0.
Supplementary information
Supplementary Information
Supplementary Tables 1–6, Figs. 1 and 2 and Notes.
Source data
Source Data for Fig. 2
Measured photometry of the transient AT 2016jka, and predicted magnifications and time delays for the AT 2016jka images, from all lens model variants.
Source Data for Extended Data Fig. 1
Locations for components of the LENSTOOL mass model of MACS J0138.
Rights and permissions
About this article
Cite this article
Rodney, S.A., Brammer, G.B., Pierel, J.D.R. et al. A gravitationally lensed supernova with an observable two-decade time delay. Nat Astron 5, 1118–1125 (2021). https://doi.org/10.1038/s41550-021-01450-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-021-01450-9
This article is cited by
-
Searching for Strong Gravitational Lenses
Space Science Reviews (2024)
-
Strong Gravitational Lensing and Microlensing of Supernovae
Space Science Reviews (2024)
-
A tiny galaxy brightening up a distant supernova
Nature Astronomy (2023)
-
Cosmological distances and Hubble tension in Einstein–Cartan theory
General Relativity and Gravitation (2023)
-
Shock cooling of a red-supergiant supernova at redshift 3 in lensed images
Nature (2022)