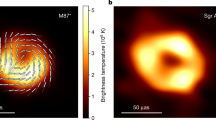
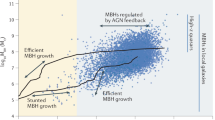
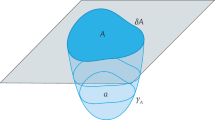
Abstract
Although black holes are objects of central importance across many fields of physics, there is no agreed upon definition for them, a fact that does not seem to be widely recognized. Physicists in different fields conceive of and reason about them in radically different, and often conflicting, ways. All those ways, however, seem sound in the relevant contexts. After examining and comparing many of the definitions used in practice, I consider the problems that the lack of a universally accepted definition leads to, and discuss whether one is in fact needed for progress in the physics of black holes. I conclude that, within reasonable bounds, the profusion of different definitions is in fact a virtue, making the investigation of black holes possible and fruitful in all the many different kinds of problems about them that physicists consider, although one must take care in trying to translate results between fields.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Ashtekar, A. & Krishnan, B. Dynamical horizons and their properties. Phys. Rev. D 68, 104030 (2003).
Hawking, S. Black hole explosions? Nature 248, 30–31 (1974).
Hawking, S. Particle creation by black holes. Commun. Math. Phys. 43, 199–220 (1975).
Curiel, E. Classical black holes are hot. Preprint at https://arxiv.org/abs/1408.3691 (2016).
Marolf, D. The black hole information problem: Past, present, and future. Rep. Prog. Phys. 80, 092001 (2017).
Unruh, W. & Wald, R. Information loss. Rep. Prog. Phys. 80, 092002 (2017).
Earman, J. Bangs, Crunches, Whimpers and Shrieks: Singularities and Acausalities in Relativistic Spacetimes (Oxford University Press, Oxford, 1995).
Earman, J. & Eisenstaedt, J. Einstein and singularities. Stud. Hist. Philos. M. P. 30, 185–235 (1999).
Eisenstaedt, J. in Einstein and the History of General Relativity (eds Howard, D. & Stachel, J.) 213–233 (Birkhäuser, Boston, 1989).
Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley and Sons Press, New York, 1972).
Genzel, R., Eckart, A., Ott, T. & Eisenhauer, F. On the nature of the dark mass in the centre of the Milky Way. Mon. Not. R. Astron. Soc. 291, 219–234 (1997).
Ghez, A., Morris, M., Becklin, E., Tanner, A. & Kremenek, T. The accelerations of stars orbiting the Milky Way’s central black hole. Nature 407, 349–351 (2000).
Hawking, S. & Ellis, G. The Large Scale Structure of Space-Time (Cambridge University Press, Cambridge, 1973).
Wald, R. General Relativity (University of Chicago Press, Chicago, 1984).
Jacobson, T. & Parentani, R. Horizon entropy. Found. Phys. 33, 323–348 (2003).
Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 14, 57–59 (1965).
Hayward, S. General laws of black hole dynamics. Phys. Rev. D 49, 6467–6474 (1994).
Ashtekar, A., Beetle, C. & Fairhurst, S. Isolated horizons: A generalization of black hole mechanics. Class. Quant. Grav. 16, L1–L7 (1999).
Bengtsson, I. & Senovilla, J. The region with trapped surfaces in spherical symmetry, its core, and their boundaries. Phys. Rev. D 83, 044012 (2011).
Penrose, R. Gravitational collapse: The role of general relativity. Rev. Nuovo Cimento 1, 257–276 (1969).
Narayan, R. & McClintock, J. Observational evidence for black holes. Preprint at https://arxiv.org/abs/1312.6698 (2013).
Collmar, W. et al. in Black Holes: Theory and Observation (eds Hehl, F., Kiefer, C. & Metzler, R. J. K.) Ch. 22, 481–489 (Springer-Verlag, Berlin, 1998).
Eckart, A. et al. The Milky Way’s supermassive black hole: How good a case is it? Found. Phys. 47, 553–624 (2017).
Wald, R. Gravitation, thermodynamics and quantum theory. Class. Quant. Grav. 16, A177–A190 (1999).
Wall, A. Ten proofs of the generalized second law. J. High Energy Phys. 2009, 021 (2009).
Maldacena, J. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 2, 231–252 (1998).
’t Hooft, G. Dimensional reduction in quantum gravity. Preprint at https://xxx.lanl.gov/abs/gr-qc/9310026 (1993).
’t Hooft, G. in Basics and Highlights in Fundamental Physics (ed. Zichichi, A.) 72–100 (World Scientific, 2001).
Bousso, R. The holographic principle for general backgrounds. Class. Quant. Grav. 17, 997 (2006).
Maldacena, J., Shenker, S. & Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 106 (2016).
Oriti, D., Pranzetti, D. & Sindoni, L. Black holes as quantum gravity condensates. Phys. Rev. D 97, 066017 (2018).
Unruh, W. Dumb holes: Analogues for black holes. Philos. T. R. Soc. A 366, 2905–2913 (2008).
Jacobson, T. in Analogue Gravity Phenomenology: Analogue Spacetimes and Horizons, from Theory to Experiment (eds Faccio, D. et al.) 1–29 (Springer-Verlag, Berlin, 2013).
Unruh, W. & Schützhold, R. Universality of the Hawking effect. Phys. Rev. D 71, 024028 (2005).
Dardashti, R., Thébault, K. & Winsberg, E. Confirmation via analogue simulation: What dumb holes could tell us about gravity. Brit. J. Philos. Sci. 68, 55–89 (2017).
Acknowledgements
I am grateful to all the many physicists and philosophers who responded to my questions with thoughtful enthusiasm—you are too many to name, but you know who you are. This Perspective would have been much poorer without the illumination of your discussions. I must, however, single out A. Ashtekar, B. Bonga, P. Chesler, B. Geroch, D. Giulini, G. ’t Hooft, T. Jacobson, C. Kiefer, A. Loeb, J. Maldacena, D. Marolf, R. Narayan, D. Oriti, C. Rovelli, K. Thébault, B. Unruh, B. Wald, D. Wallace, and S.-T. Yau for supererogatory input and further discussion. I thank B. Unruh and B. Wald also for their recollections of the attitude of relativists in the 1960s and 1970s to black holes, as well as A. Loeb and R. Narayan for discussion about the reception of the idea in the community of astrophysicists at the same time. Some of this work was completed at the Black Hole Initiative at Harvard University, which is funded through a grant from the John Templeton Foundation. The rest was completed at the Munich Center for Mathematical Philosophy, in part funded by a grant from the Deutsche Forschungsgemeinschaft (grant number CU 338/1-1 AOBJ 628412).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Curiel, E. The many definitions of a black hole. Nat Astron 3, 27–34 (2019). https://doi.org/10.1038/s41550-018-0602-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-018-0602-1
This article is cited by
-
Penrose’s 1965 singularity theorem: from geodesic incompleteness to cosmic censorship
General Relativity and Gravitation (2022)
-
Singularities, Black Holes, and Cosmic Censorship: A Tribute to Roger Penrose
Foundations of Physics (2021)
-
Why Not a Sound Postulate?
Foundations of Physics (2021)
-
The Devil in the (Implicit) Details
International Journal of Theoretical Physics (2021)
-
Testing the nature of dark compact objects: a status report
Living Reviews in Relativity (2019)