Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Equation of state of iron under core conditions of large rocky exoplanets

Nature Astronomy volume 2, pages 452–458 (2018)Cite this article

Subjects

An Author Correction to this article was published on 24 April 2018

This article has been updated

Abstract

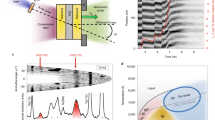
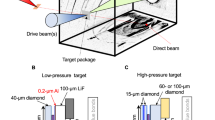
The recent discovery of thousands of planets outside our Solar System raises fundamental questions about the variety of planetary types and their corresponding interior structures and dynamics. To better understand these objects, there is a strong need to constrain material properties at the extreme pressures found within planetary interiors1,2. Here we used high-powered lasers at the National Ignition Facility to ramp compress iron over nanosecond timescales to 1.4 TPa (14 million atmospheres)—a pressure four times higher than for previous static compression data. A Lagrangian sound-speed analysis was used to determine pressure, density and sound speed along a continuous isentropic compression path. Our peak pressures are comparable to those predicted at the centre of a terrestrial-type exoplanet of three to four Earth masses3, representing the first absolute equation of state measurements for iron at such conditions. These results provide an experiment-based mass–radius relationship for a hypothetical pure iron planet that can be used to evaluate plausible compositional space for large, rocky exoplanets.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Free-surface velocity measurements from a dynamically compressed multi-thickness Fe sample.
Fig. 2: Isentropic P–ρ path of Fe to 3.7 Earth-mass planet core conditions.
Fig. 3: Sound velocity and Grüneisen parameter as a function of density for iron.
Fig. 4: Mass–radius relationships for homogeneous-composition planets.

Similar content being viewed by others

Change history

  • 24 April 2018

    In the version of this Letter originally published, in the Acknowledgements, the surname of M. Herrmann was misspelt as ‘Hermann’. This has now been corrected.

References

  1. Valencia, D., O’Connell, R. J. & Sasselov, D. Internal structure of massive terrestrial planets. Icarus 181, 545–554 (2006).

    Article  ADS  Google Scholar 

  2. Swift, D. C. et al. Mass–radius relationships for exoplanets. Astrophys. J. 744, 59 (2012).

    Article  ADS  Google Scholar 

  3. Wagner, F. W., Tosi, N., Sohl, F., Rauer, H. & Spohn, T. Rocky super-Earth interiors— Structure and internal dynamics of CoRoT-7b and Kepler-10b. Astron. Astrophys. 541, A103 (2012).

    Article  ADS  Google Scholar 

  4. Marcy, G. W. et al. Occurrence and core-envelope structure of 1–4x Earth-size planets around Sun-like stars. Proc. Natl Acad. Sci. USA 111, 12655–12660 (2014).

    Article  ADS  Google Scholar 

  5. Santos, N. et al. Constraining planet structure from stellar chemistry: the cases of CoRoT-7, Kepler-10, and Kepler-93. Astron. Astrophys. 580, L13 (2015).

    Article  ADS  Google Scholar 

  6. Gillon, M. et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 542, 456–460 (2017).

    Article  ADS  Google Scholar 

  7. Noack, L. et al. Can the interior structure influence the habitability of a rocky planet? Planet. Space Sci. 98, 14–29 (2014).

    Article  ADS  Google Scholar 

  8. Foley, B. J. & Driscoll, P. E. Whole planet coupling between climate, mantle, and core: implications for rocky planet evolution. Geochem. Geophys. Geosyst. 17, 1885–1914 (2016).

    Article  ADS  Google Scholar 

  9. Marcus, R. A., Stewart, S. T., Sasselov, D. & Hernquist, L. Collisional stripping and disruption of super-Earths. Astrophys. J. Lett. 700, L118 (2009).

    Article  ADS  Google Scholar 

  10. Dewaele, A. et al. Quasihydrostatic equation of state of iron above 2 Mbar. Phys. Rev. Lett. 97, 215504 (2006).

    Article  ADS  Google Scholar 

  11. Cohen, R. E. & Mukherjee, S. Non-collinear magnetism in iron at high pressures. Phys. Earth Planet. Inter. 143, 445–453 (2004).

    Article  ADS  Google Scholar 

  12. Stixrude, L. Structure of Iron to 1 Gbar and 40 000 K. Phys. Rev. Lett. 108, 055505 (2012).

    Article  ADS  Google Scholar 

  13. Lazicki, A. et al. X-ray diffraction of solid tin to 1.2 TPa. Phys. Rev. Lett. 115, 075502 (2015).

    Article  ADS  Google Scholar 

  14. Amadou, N. et al. Probing iron at super-Earth core conditions. Phys. Plasmas 22, 022705 (2015).

    Article  ADS  Google Scholar 

  15. Smith, R. F. et al. Ramp compression of diamond to five terapascals. Nature 511, 330–333 (2014).

    Article  ADS  Google Scholar 

  16. Smith, R. F. et al. Time-dependence of the alpha to epsilon phase transformation in iron. J. Appl. Phys. 114, 223507 (2013).

    Article  ADS  Google Scholar 

  17. Ping, Y. et al. Solid iron compressed up to 560 GPa. Phys. Rev. Lett. 111, 065501 (2013).

    Article  ADS  Google Scholar 

  18. Ahrens, T. J. Mineral Physics and Crystallography: a Handbook of Physical Constants 143–184 (American Geophysical Union, Washington, DC, 1995).

  19. Wang, J. et al. Ramp compression of iron to 273 GPa. J. Appl. Phys. 114, 023513 (2013).

    Article  ADS  Google Scholar 

  20. Vinet, P., Ferrante, J., Rose, J. & Smith, J. Compressibility of solids. J. Geophys. Res. Solid Earth 92, 9319–9325 (1987).

    Article  Google Scholar 

  21. Kerley, G. I. Multiphase Equation of State for Iron. Report No. SAND93-0027 (Sandia National Laboratory, 1993).

  22. Birch, F. Composition of the Earth’s mantle. Geophys. J. Int. 4, 295–311 (1961).

    Article  ADS  Google Scholar 

  23. Brown, J. M. & McQueen, R. G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 91, 7485–7494 (1986).

    Article  ADS  Google Scholar 

  24. Murphy, C. A., Jackson, J. M., Sturhahn, W. & Chen, B. Grüneisen parameter of HCP-Fe to 171 GPa. Geophys. Res. Lett. 38, L24306 (2011).

  25. Anderson, O. L. The Grüneisen parameter for iron at outer core conditions and the resulting conductive heat and power in the core. Phys. Earth Planet. Inter. 109, 179–197 (1998).

    Article  ADS  Google Scholar 

  26. Zapolsky, H. S. & Salpeter, E. E. The mass–radius relation for cold spheres of low mass. Astrophys. J. 158, 809–813 (1969).

    Article  ADS  Google Scholar 

  27. Valencia, D., Ikoma, M., Guillot, T. & Nettelmann, N. Composition and fate of short-period super-Earths—the case of CoRoT-7b. Astron. Astrophys. 516, A20 (2010).

    Article  ADS  Google Scholar 

  28. Howe, A. R., Burrows, A. & Verne, W. Mass–radius relations and core-envelope decompositions of super-Earths and sub-Neptunes. Astrophys. J. 787, 173 (2014).

    Article  ADS  Google Scholar 

  29. Akeson, R. L. et al. The NASA exoplanet archive: data and tools for exoplanet research. Publ. Astron. Soc. Pac. 125, 989–999 (2013).

    Article  ADS  Google Scholar 

  30. Mocquet, A., Grasset, O. & Sotin, C. Very high-density planets: a possible remnant of gas giants. Philos. Trans. R. Soc. A 372, 20130164 (2014).

    Article  ADS  Google Scholar 

  31. Marcus, R. A., Sasselov, D., Hernquist, L. & Stewart, S. T. Minimum radii of super-earths: constraints from giant impacts. Astrophys. J. Lett. 712, L73 (2010).

    Article  ADS  Google Scholar 

  32. Moody, J. D. et al. Progress in hohlraum physics for the National Ignition Facility. Phys. Plasmas 21, 056317 (2014).

    Article  ADS  Google Scholar 

  33. Mirkarimi, P., Bettencourt, K., Teslich, N. & Peterson, S. Recent advances in the fabrication of very thick, multistepped iron and tantalum films for EOS targets. Fusion Sci. Technol. 63, 282–287 (2013).

    Article  Google Scholar 

  34. Celliers, P. M. et al. Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility. Rev. Sci. Instrum. 75, 4916–4929 (2004).

    Article  ADS  Google Scholar 

  35. Fowles, R. & Williams, R. F. Plane stress wave propagation in solids. J. Appl. Phys. 41, 360–363 (1970).

    Article  ADS  Google Scholar 

  36. Cowperthwaite, M. & Williams, R. Determination of constitutive relationships with multiple gauges in nondivergent waves. J. Appl. Phys. 42, 456–462 (1971).

    Article  ADS  Google Scholar 

  37. Cagnoux, J., Chartagnac, P., Hereil, P., Perez, M. & Seaman, L. Lagrangian analysis. Modern tool of the dynamics of solids. Ann. Phys. 12, 451–524 (1987).

    Article  Google Scholar 

  38. Aidun, J. B. & Gupta, Y. M. Analysis of Lagrangian gauge measurements of simple and non-simple plane waves. J. Appl. Phys. 69, 6998–7014 (1991).

    Article  ADS  Google Scholar 

  39. Rothman, S. D. et al. Measurement of the principal isentropes of lead and lead-antimony alloy to ~400 kbar by quasi-isentropic compression. J. Phys. D 38, 733–740 (2005).

    Article  ADS  Google Scholar 

  40. Larsen, J. T. & Lane, S. M. HYADES—a plasma hydrodynamics code for dense plasma studies. J. Quant. Spectrosc. Radiat. Transf. 51, 179–186 (1994).

    Article  ADS  Google Scholar 

  41. Erskine, D. Speckle-adaptive VISAR fringe analysis technique. AIP Conf. Proc. 1793, 160017 (2017).

    Article  Google Scholar 

  42. Fowles, G. R. Shock wave compression of hardened and annealed 2024 aluminum. J. Appl. Phys. 32, 1475–1487 (1961).

    Article  ADS  Google Scholar 

  43. Hill, R. The Mathematical Theory of Plasticity (Oxford Univ. Press, New York, 1950).

    MATH  Google Scholar 

  44. Ahrens, T. J. in High-Pressure Shock Compression of Solids 75–114 (Springer, New York, 1993).

  45. Brown, J. M. & McQueen, R. G. in High-Pressure Research in Geophysics (eds Akimoto, S. & Manghnani, M. H.) 611–623 (Riedel, Boston, 1982).

  46. Taylor, G. I. & Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. A 143, 307–326 (1934).

    Article  ADS  Google Scholar 

  47. Zaera, R., Rodriguez-Martinez, J. A. & Rittel, D. On the Taylor–Quinney coefficient in dynamically phase transforming materials. Application to 304 stainless steel. Int. J. Plast. 40, 185–201 (2013).

    Article  Google Scholar 

  48. Gleason, A. E. & Mao, W. L. Strength of iron at core pressures and evidence for a weak Earth’s inner core. Nat. Geosci. 6, 571–574 (2013).

    Article  ADS  Google Scholar 

  49. Steinberg, D. J., Cochran, S. G. & Guinan, M. W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 51, 1498–1504 (1980).

    Article  ADS  Google Scholar 

  50. Smith, R. F. et al. High strain-rate plastic flow in Al and Fe. J. Appl. Phys. 110, 123515 (2011).

    Article  ADS  Google Scholar 

  51. Huntington, C. M. et al. Investigating iron material strength up to 1 Mbar using Rayleigh–Taylor growth measurements. AIP Conf. Proc. 1793, 110007 (2017).

    Article  Google Scholar 

  52. Nguyen, J. H. & Holmes, N. C. Melting of iron at the physical conditions of the Earth’s core. Nature 427, 339–342 (2004).

    Article  ADS  Google Scholar 

  53. Zhang, W.-J., Liu, Z.-Y., Liu, Z.-L. & Cai, L.-C. Melting curves and entropy of melting of iron under Earth's core conditions. Phys. Earth Planet. Inter. 244, 69–77 (2015).

    Article  ADS  Google Scholar 

  54. Luo, F., Cheng, Y., Chen, X.-R., Cai, L.-C. & Jing, F.-Q. The melting curves and entropy of iron under high pressure. J. Chem. Eng. Data 56, 2063–2070 (2011).

    Article  Google Scholar 

  55. McQueen, R. G., Marsh, S. P. & Fritz, J. N. Hugoniot equation of state of twelve rocks. J. Geophys. Res. 72, 4999–5036 (1967).

    Article  ADS  Google Scholar 

  56. Duffy, T. S. & Ahrens, T. J. in High-Pressure Research: Application to Earth and Planetary Sciences 353–361 (Terra Scientific Publishing Company, Tokyo and American Geophysical Union, Washington D.C., 1992).

  57. Dubrovinsky, L. S., Saxena, S. K., Tutti, F., Rekhi, S. & LeBehan, T. In situ X-ray study of thermal expansion and phase transition of iron at multimegabar pressure. Phys. Rev. Lett. 84, 1720–1723 (2000).

    Article  ADS  Google Scholar 

  58. Duffy, T. S. & Ahrens, T. K. Thermal expansion of mantle and core materials at very high pressures. Geophys. Res. Lett. 20, 1103–1106 (1993).

    Article  ADS  Google Scholar 

  59. Antonangeli, D. & Ohtani, E. Sound velocity of HCP-Fe at high pressure: experimental constraints, extrapolations and comparison with seismic models. Progress. Earth Planet. Sci. 2, 3 (2015).

    Article  ADS  Google Scholar 

  60. Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).

    Article  ADS  Google Scholar 

  61. Sakaiya, T. et al. Sound velocity and density measurements of liquid iron up to 800 GPa: a universal relation between Birch’s law coefficients for solid and liquid metals. Earth Planet. Sci. Lett. 392, 80–85 (2014).

  62. Dubrovinsky, L. S., Saxena, S. K., Tutti, F., Rekhi, S. & LeBehan, T. Gruneisen parameter of epsilon-iron up to 300 GPa from in-situ X-ray study. Am. Mineral. 85, 386–389 (2000).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank the laser and target fabrication staff of the NIF, G. Wisoff, M. Herrmann and B. Goldstein. Beam time was granted through the Science Use of NIF programme. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract number DE-AC52-07NA27344, with additional support from the Department of Energy, University of California and Miller Institute for Basic Research in Science. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.

Author information

Authors and Affiliations

  1. Lawrence Livermore National Laboratory, Livermore, CA, USA

    Raymond F. Smith, Dayne E. Fratanduono, David G. Braun, Peter M. Celliers, Suzanne J. Ali, Amalia Fernandez-Pañella, Richard G. Kraus, Damian C. Swift, Gilbert W. Collins & Jon H. Eggert

  2. Department of Geosciences, Princeton University, Princeton, NJ, USA

    Thomas S. Duffy & June K. Wicks

  3. Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD, USA

    June K. Wicks

  4. Departments of Mechanical Engineering, Physics and Astronomy, and the Laboratory for Laser Energetics, University of Rochester, Rochester, NY, USA

    Gilbert W. Collins

Authors
  1. Raymond F. Smith
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dayne E. Fratanduono
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David G. Braun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Thomas S. Duffy
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. June K. Wicks
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Peter M. Celliers
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Suzanne J. Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Amalia Fernandez-Pañella
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Richard G. Kraus
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Damian C. Swift
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Gilbert W. Collins
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Jon H. Eggert
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.F.S., D.E.F., D.G.B. and J.H.E. designed, executed and analysed the data from the ramp compression experiments. P.M.C. helped with the analysis of the VISAR data. S.J.A. and A.F.P. performed hydrocode modelling to help determine the systematic uncertainties in the measurement. T.S.D., J.K.W. and D.C.S. performed the comparisons of experimental data with EOS models and theory. R.G.K and G.W.C. helped interpret the data.

Corresponding author

Correspondence to Raymond F. Smith.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figures 1–7, Supplementary Table 1.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Smith, R.F., Fratanduono, D.E., Braun, D.G. et al. Equation of state of iron under core conditions of large rocky exoplanets. Nat Astron 2, 452–458 (2018). https://doi.org/10.1038/s41550-018-0437-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41550-018-0437-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing