Abstract
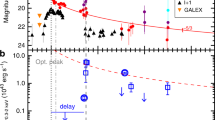
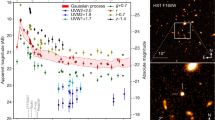
When a star passes within the tidal radius of a supermassive black hole, it will be torn apart1. For a star with the mass of the Sun (M⊙) and a non-spinning black hole with a mass <108M⊙, the tidal radius lies outside the black hole event horizon2 and the disruption results in a luminous flare3–6. Here we report observations over a period of ten months of a transient, hitherto interpreted7 as a superluminous supernova8. Our data show that the transient rebrightened substantially in the ultraviolet and that the spectrum went through three different spectroscopic phases without ever becoming nebular. Our observations are more consistent with a tidal disruption event than a superluminous supernova because of the temperature evolution6, the presence of highly ionized CNO gas in the line of sight9 and our improved localization of the transient in the nucleus of a passive galaxy, where the presence of massive stars is highly unlikely10,11. While the supermassive black hole has a mass >108M⊙12,13, a star with the same mass as the Sun could be disrupted outside the event horizon if the black hole were spinning rapidly14. The rapid spin and high black hole mass can explain the high luminosity of this event.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Rees, M. J. Tidal disruption of stars by black holes of 106–108 solar masses in nearby galaxies. Nature 333, 523–528 (1988).
Hills, J. G. Possible power source of Seyfert galaxies and QSOs. Nature 254, 295–298 (1975).
van Velzen, S. et al. Optical discovery of probable stellar tidal disruption flares. Astrophys. J. 741, 73 (2011).
Gezari, S. et al. An ultraviolet-optical flare from the tidal disruption of a helium-rich stellar core. Nature 485, 217–220 (2012).
Arcavi, I. et al. A continuum of H- to He-rich tidal disruption candidates with a preference for E+A galaxies. Astrophys. J. 793, 38 (2014).
Holoien, T. W.-S. et al. ASASSN-14ae: a tidal disruption event at 200 Mpc. Mon. Not. R. Astron. Soc. 445, 3263–3277 (2014).
Dong, S. et al. ASASSN-15lh: a highly super-luminous supernova. Science 351, 257–260 (2016).
Quimby, R. M. et al. Hydrogen-poor superluminous stellar explosions. Nature 474, 487–489 (2011).
Cenko, S. B. et al. An ultraviolet spectrum of the tidal disruption flare ASASSN-14li. Astrophys. J. Lett. 818, L32 (2016).
Lunnan, R. et al. Hydrogen-poor superluminous supernovae and long-duration gamma-ray bursts have similar host galaxies. Astrophys. J. 787, 138 (2014).
Leloudas, G. et al. Spectroscopy of superluminous supernova host galaxies. A preference of hydrogen-poor events for extreme emission line galaxies. Mon. Not. R. Astron. Soc. 449, 917–932 (2015).
Reines, A. E. & Volonteri, M. Relations between central black hole mass and total galaxy stellar mass in the local universe. Astrophys. J. 813, 82 (2015).
McConnell, N. J. & Ma, C.-P. Revisiting the scaling relations of black hole masses and host galaxy properties. Astrophys. J. 764, 184 (2013).
Kesden, M. Tidal-disruption rate of stars by spinning supermassive black holes. Phys. Rev. D 85, 024037 (2012).
Mazzali, P. A., Sullivan, M., Pian, E., Greiner, J. & Kann, D. A. Spectrum formation in superluminous supernovae (type I). Mon. Not. R. Astron. Soc. 458, 3455–3465 (2016).
Strubbe, L. E. & Quataert, E. Spectroscopic signatures of the tidal disruption of stars by massive black holes. Mon. Not. R. Astron. Soc. 415, 168–180 (2011).
Pastorello, A. et al. Ultra-bright optical transients are linked with type Ic supernovae. Astrophys. J. 724, L16–L21 (2010).
Brown, P. J. et al. ASASSN-15lh: a superluminous ultraviolet rebrightening observed by Swift and Hubble. Astrophys. J. 828, 3 (2016).
de Ugarte Postigo, A. et al. The distribution of equivalent widths in long GRB afterglow spectra. Astron. Astrophys. 548, A11 (2012).
Brown, P. J. Ultraviolet rebrightening of superluminous supernova ASASSN-15lh. Astron. Telegr. 8086 (2015).
Godoy-Rivera, D. et al. The unexpected, long-lasting, UV rebrightening of the super-luminous supernova ASASSN-15lh. Preprint at https://arxiv.org/abs/1605.00645 (2016).
Inserra, C. et al. Super-luminous type Ic supernovae: catching a magnetar by the tail. Astrophys. J. 770, 128 (2013).
Nicholl, M. et al. Superluminous supernovae from PESSTO. Mon. Not. R. Astron. Soc. 444, 2096–2113 (2014).
Chen, T.-W. et al. The host galaxy and late-time evolution of the superluminous supernova PTF12dam. Mon. Not. R. Astron. Soc. 452, 1567–1586 (2015).
Howell, D. A. et al. Two superluminous supernovae from the early universe discovered by the supernova legacy survey. Astrophys. J. 779, 98 (2013).
Metzger, B. D., Margalit, B., Kasen, D. & Quataert, E. The diversity of transients from magnetar birth in core collapse supernovae. Mon. Not. R. Astron. Soc. 454, 3311–3316 (2015).
Sukhbold, T. & Woosley, S. E. The most luminous supernovae. Astrophys. J. Lett. 820, L38 (2016).
Yan, L. et al. Detection of broad Hα emission lines in the late-time spectra of a hydrogen-poor superluminous supernova. Astrophys. J. 814, 108 (2015).
Leloudas, G. et al. Polarimetry of the superluminous supernova LSQ14mo: no evidence for significant deviations from spherical symmetry. Astrophys. J. Lett. 815, L10 (2015).
Stone, N. C. & Metzger, B. D. Rates of stellar tidal disruption as probes of the supermassive black hole mass function. Mon. Not. R. Astron. Soc. 455, 859–883 (2016).
Kochanek, C. S. Tidal disruption event demographics. Mon. Not. R. Astron. Soc. 461, 371–384 (2016).
Reynolds, C. S. Measuring black hole spin using X-ray reflection spectroscopy. Space Sci. Rev. 183, 277–294 (2014).
Piran, T., Svirski, G., Krolik, J., Cheng, R. M. & Shiokawa, H. Disk formation versus disk accretion – what powers tidal disruption events? Astrophys. J. 806, 164 (2015).
Dai, L., McKinney, J. C. & Miller, M. C. Soft X-Ray Temperature Tidal Disruption Events from Stars on Deep Plunging Orbits. Astrophys. J. Lett. 812, L39 (2015).
Guillochon, J., Manukian, H. & Ramirez-Ruiz, E. PS1-10jh: the disruption of a main-sequence star of near-solar composition. Astrophys. J. 783, 23 (2014).
Planck Collaboration XVI. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 571, A16 (2014).
Melchior, P. et al. Optical broad-band photometry and reference image for APMUKS(BJ) B215839.70-615403.9 / ASASSN-15lh from the Dark Energy Survey. Astron. Telegr. 7843 (2015).
Prieto, J. L. et al. APMUKS(BJ) B215839.70-615403.9: The massive host galaxy candidate of ASASSN-15lh. Astron. Telegr. 7776 (2015).
Schlafly, E. F. & Finkbeiner, D. P. Measuring reddening with sloan digital sky survey stellar spectra and recalibrating SFD. Astrophys. J. 737, 103 (2011).
Bruzual, G. & Charlot, S. Stellar population synthesis at the resolution of 2003. Mon. Not. R. Astron. Soc. 344, 1000–1028 (2003).
Arnouts, S. et al. Measuring and modelling the redshift evolution of clustering: the Hubble Deep Field North. Mon. Not. R. Astron. Soc. 310, 540–556 (1999).
Ilbert, O. et al. Accurate photometric redshifts for the CFHT legacy survey calibrated using the VIMOS VLT deep survey. Astron. Astrophys. 457, 841–856 (2006).
Chabrier, G. Galactic stellar and substellar initial mass function. Publ. Astron. Soc. Pacif. 115, 763–795 (2003).
Calzetti, D. et al. The dust content and opacity of actively star-forming galaxies. Astrophys. J. 533, 682–695 (2000).
Kennicutt, R. C. Jr Star formation in galaxies along the Hubble sequence. Annu. Rev. Astron. Astrophys. 36, 189–232 (1998).
Vreeswijk, P. M. et al. The hydrogen-poor superluminous supernova iPTF 13ajg and its host galaxy in absorption and emission. Astrophys. J. 797, 24 (2014).
Christensen, L. et al. A high signal-to-noise ratio composite spectrum of gamma-ray burst afterglows. Astrophys. J. 727, 73 (2011).
Fox, A. J., Petitjean, P., Ledoux, C. & Srianand, R. Hot halos around high redshift protogalaxies. Observations of OVI and NV absorption in damped Lyman-α systems. Astron. Astrophys. 465, 171–184 (2007).
Fox, A. J., Ledoux, C., Vreeswijk, P. M., Smette, A. & Jaunsen, A. O. High-ion absorption in seven GRB host galaxies at z = 2-4. Evidence for both circumburst plasma and outflowing interstellar gas. Astron. Astrophys. 491, 189–207 (2008).
Kochanek, C. S. Abundance anomalies in tidal disruption events. Mon. Not. R. Astron. Soc. 458, 127–134 (2016).
Miller, J. M. et al. Flows of X-ray gas reveal the disruption of a star by a massive black hole. Nature 526, 542–545 (2015).
Dopita, M. et al. The Wide Field Spectrograph (WiFeS). Astrophys Space Sci. 310, 255–268 (2007).
Dopita, M. et al. The Wide Field Spectrograph (WiFeS): performance and data reduction. Astrophys Space Sci. 327, 245–257 (2010).
Smartt, S. J. et al. PESSTO: survey description and products from the first data release by the Public ESO Spectroscopic Survey of Transient Objects. Astron. Astrophys. 579, A40 (2015).
Jenness, T. & Economou, F. ORAC-DR: a generic data reduction pipeline infrastructure. Astron. Comput. 9, 40–48 (2015).
Brown, P. J. et al. The absolute magnitudes of type Ia supernovae in the ultraviolet. Astrophys. J. 721, 1608–1626 (2010).
Sault, R. J., Teuben, P. J. & Wright, M. C. H. A retrospective view of MIRIAD. In Astronomical Data Analysis Software and Systems IV Vol. 77 (eds Shaw, R. A., Payne, H. E. & Hayes, J. J. E. ) 433 (Astronomical Society of the Pacific Conference Series, 1995).
McMullin, J. P., Waters, B., Schiebel, D., Young, W. & Golap, K. CASA architecture and applications. In Astronomical Data Analysis Software and Systems XVI Vol. 376 (eds Shaw, R. A., Hill, F. & Bell, D. J. ) 127 (Astronomical Society of the Pacific Conference Series, 2007).
Kool, E. C. et al. Radio non-detection of ASASSN-15lh = SN2015L. Astron. Telegr. 8388 (2015).
Kraft, R. P., Burrows, D. N. & Nousek, J. A. Determination of confidence limits for experiments with low numbers of counts. Astrophys. J. 374, 344–355 (1991).
Helene, O. Errors in experiments with small numbers of events. Nucl. Instrum. Methods Phys. Res. A 228, 120–128 (1984).
van Velzen, S. et al. A radio jet from the optical and x-ray bright stellar tidal disruption flare ASASSN-14li. Science 351, 62–65 (2016).
Levan, A. J. et al. An extremely luminous panchromatic outburst from the nucleus of a distant galaxy. Science 333, 199–202 (2011).
Tchekhovskoy, A., Metzger, B. D., Giannios, D. & Kelley, L. Z. Swift J1644+57 gone MAD: the case for dynamically important magnetic flux threading the black hole in a jetted tidal disruption event. Mon. Not. R. Astron. Soc. 437, 2744–2760 (2014).
Guillochon, J. & Ramirez-Ruiz, E. Hydrodynamical simulations to determine the feeding rate of black holes by the tidal disruption of stars: the importance of the impact parameter and stellar structure. Astrophys. J. 767, 25 (2013).
Stone, N., Sari, R. & Loeb, A. Consequences of strong compression in tidal disruption events. Mon. Not. R. Astron. Soc. 435, 1809–1824 (2013).
Bersten, M. C., Benvenuto, O. G., Orellana, M. & Nomoto, K. The unusual super-luminous supernovae SN 2011kl and ASASSN-15lh. Astrophys. J. Lett. 817, L8 (2016).
Kozyreva, A., Hirschi, R., Blinnikov, S. & den Hartogh, J. How much radioactive nickel does ASASSN-15lh require? Mon. Not. R. Astron. Soc. 459, L21–L25 (2016).
Chatzopoulos, E. et al. Extreme supernova models for the super-luminous transient ASASSN-15lh. Astrophys. J. 828, 94 (2016).
Metzger, B. D. & Stone, N. C. A bright year for tidal disruptions. Mon. Not. R. Astron. Soc. 461, 948–966 (2016).
Coughlin, E. R. & Begelman, M. C. Hyperaccretion during tidal disruption events: weakly bound debris envelopes and jets. Astrophys. J. 781, 82 (2014).
Roth, N., Kasen, D., Guillochon, J. & Ramirez-Ruiz, E. The X-Ray through optical fluxes and line strengths of tidal disruption events. Astrophys. J. 827, 3 (2016).
Hayasaki, K., Stone, N. & Loeb, A. Finite, intense accretion bursts from tidal disruption of stars on bound orbits. Mon. Not. R. Astron. Soc. 434, 909–924 (2013).
Shiokawa, H., Krolik, J. H., Cheng, R. M., Piran, T. & Noble, S. C. General relativistic hydrodynamic simulation of accretion flow from a stellar tidal disruption. Astrophys. J. 804, 85 (2015).
Hayasaki, K., Stone, N. & Loeb, A. Circularization of tidally disrupted stars around spinning supermassive black holes. Mon. Not. R. Astron. Soc. 461, 3760–3780 (2016).
Guillochon, J. & Ramirez-Ruiz, E. A dark year for tidal disruption events. Astrophys. J. 809, 166 (2015).
Ulmer, A. Flares from the tidal disruption of stars by massive black holes. Astrophys. J. 514, 180–187 (1999).
Strubbe, L. E. & Quataert, E. Optical flares from the tidal disruption of stars by massive black holes. Mon. Not. R. Astron. Soc. 400, 2070–2084 (2009).
Kesden, M. Black-hole spin dependence in the light curves of tidal disruption events. Phys. Rev. D 86, 064026 (2012).
Carter, B. & Luminet, J.-P. Tidal compression of a star by a large black hole. I: mechanical evolution and nuclear energy release by proton capture. Astron. Astrophys. 121, 97–113 (1983).
Merritt, D., Alexander, T., Mikkola, S. & Will, C. M. Testing properties of the galactic center black hole using stellar orbits. Phys. Rev. D 81, 062002 (2010).
Beloborodov, A. M., Illarionov, A. F., Ivanov, P. B. & Polnarev, A. G. Angular momentum of a supermassive black hole in a dense star cluster. Mon. Not. R. Astron. Soc. 259, 209–217 (1992).
Marck, J.-A. Solution to the equations of parallel transport in Kerr geometry; tidal tensor. Proc. R. Soc. Lond. A 385, 431–438 (1983).
Yaron, O. & Gal-Yam, A. WISeREP: an interactive supernova data repository. Publ. Astron. Soc. Pacif. 124, 668–681 (2012).
Acknowledgements
We acknowledge support from the European Union FP7 programme through the following European Research Council grants: 320360 (M.F., H.C.), 647208 (P.G.J.), 291222 (S.J.S.), 615929 (M.S.). We also acknowledge: Einstein Postdoctoral Fellowship PF5-160145 (N.C.S.), Hubble Postdoctoral Fellowship HST-HF2-51350 (S.v.V.), STFC grants ST/I001123/1 ST/L000709/1 (S.J.S.) and ST/L000679/1 (M.S.), Australian Research Council Future Fellowship FT140101082 (J.C.A.M.-J.), a Royal Society University Research Fellowship (J.R.M.), a Sofja Kovalevskaja Award to P. Schady (T.Kr., T.-W.C.), a Ramón y Cajal fellowship and the Spanish research project AYA 2014-58381 (A.de U.P.), CONICYT-Chile FONDECYT grants 3130488 (S.K.), 3140534 (S.S.), 3140563 (H.K.), 3150238 (C.R.-C.), a PRIN-INAF 2014 project (N.E.-R.), support from IDA (D.M.), an Ernest Rutherford Fellowship (K.M.), CAASTRO project number CE110001020 (B.E.T.), National Science Foundation grant AST 11-09881 and NASA grant HST-AR-13726.02 (J.C.W.). This work used observations from the Las Cumbres Observatory Global Telescope Network (LCOGT) and was based upon work supported by National Science Foundation grant 1313484. The Australia Telescope Compact Array is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by Commonwealth Scientific and Industrial Research Organisation. This work was based partially on observations collected as part of the Public European Southern Observatory Spectroscopic Survey for Transient Objects Survey (PESSTO) under European Southern Observatory (ESO) programmes 188.D-3003 and 191.D-0935, and on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 095.D-0633. We thank M. Della Valle for comments.
Author information
Authors and Affiliations
Contributions
G.L. coordinated the PESSTO observations, was principal investigator (PI) of the FORS2 program, analysed the data and wrote the paper. M.F. provided the astrometric localization and reduced the PESSTO spectra. N.C.S. calculated the relationship between the black hole spin and the Hills mass and edited the manuscript. S.v.V. performed the Swift photometry. P.G.J. analysed the X-Ray Multi-Mirror Mission data and helped coordinate the project. I.A. is the PESSTO PI for TDEs and provided LCOGT data. C.F. made the LCOGT photometry. J.R.M. reduced the FORS2 spectra. S.J.S. is the PI of PESSTO and helped coordinate the project. T.Kr. provided the spectral energy distribution fit of the host galaxy. J.C.A.M.-J. provided the radio observations. P.M.V. helped with the analysis of the spectra. G.L., M.F., N.C.S., S.v.V., P.G.J., I.A., S.J.S., J.C.A.M.-J., A.G.-Y. and P.A.M. contributed to the discussions. A.d.U.P. and A.De C. worked on the UV spectrum. D.A.H. is the PI of the LCOGT observations. C.I. and O.Y. are PESSTO builders and helped with the analysis. F.P., D.M., J.S. and J.C.W. provided FORS2 data and analysis. M.C. and B.E.T. provided the WIFES spectra. S.S. and S.K. provided the Magellan spectrum. G.H., C.V.McC. and S.V. obtained and reduced LCOGT data. E.K., K.M., K.W.S., M.S., and D.R.Y. are PESSTO builders and C.A., J.H., S.M., T.-W.C., T.Ka., S.P., C.R.-C., H.K., M.N., J.L., N.E.-R., H.C., I.B., J.J., M.R.M. contributed PESSTO observations or data reductions. Many authors provided comments on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1–8, Supplementary Tables 1–2 (PDF 1050 kb)
Rights and permissions
About this article
Cite this article
Leloudas, G., Fraser, M., Stone, N. et al. The superluminous transient ASASSN-15lh as a tidal disruption event from a Kerr black hole. Nat Astron 1, 0002 (2017). https://doi.org/10.1038/s41550-016-0002
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41550-016-0002
This article is cited by
-
The Birth of a Relativistic Jet Following the Disruption of a Star by a Cosmological Black Hole
Nature Astronomy (2022)
-
The Process of Stellar Tidal Disruption by Supermassive Black Holes
Space Science Reviews (2021)
-
Distinguishing Tidal Disruption Events from Impostors
Space Science Reviews (2021)
-
X-ray flares from the stellar tidal disruption by a candidate supermassive black hole binary
Nature Communications (2020)
-
Optical-Ultraviolet Tidal Disruption Events
Space Science Reviews (2020)