Abstract
Pipe failure prediction models are essential for informing proactive management decisions. This study aims to establish a reliable prediction model returning the probability of pipe failure using a gradient boosted tree model, and a specific segmentation and grouping of pipes on a 1 km grid that associates localised characteristics. The model is applied to an extensive UK network with approximately 40,000 km of pipeline and a 14-year failure history. The model was evaluated using the Receiver Operator Curve and Area Under the Curve (0.89), briers score (0.007) and Mathews Correlation Coefficient (0.27) for accuracy, indicating acceptable predictions. A weighted risk analysis is used to identify the consequence of a pipe failure and provide a graphical representation of high-risk pipes for decision makers. The weighted risk analysis provided an important step to understanding the consequences of the predicted failure. The model can be used directly in strategic planning, which sets long-term key decisions regarding maintenance and potential replacement of pipes.
Similar content being viewed by others
Introduction
Many Water Distribution Networks (WDN) are ageing and are in the closing phase of their design life, leading to pipe failures, leaks, and wasted water, causing environmental, economic, and societal impacts. With mounting pressure brought about by increased water demand and climate change impacts, leading to stress on water supply, and water regulators imposing heavy fines for not meeting performance objectives1, there is an urgency to reduce the effects of pipe failures through appropriate proactive management. Proactive management is the desired approach for managing WDNs, seeking to pre-empt issues and set levels of acceptable risk. Traditionally, proactive management is achieved through prioritising the replacement or repair of pipes using simplistic rank likelihood models, expert judgment, and detailed network knowledge to target critical areas of the network that have historically failed regularly2. However, this simplistic approach is not suitable for managing WDNs with complex mechanisms of pipe failure, and compound associated risks including loss of water causing damage to properties and infrastructure, potential disruption during repair, water supply discontinuity and economic costs of repair and replacement. Proactive management requires understanding future pipe performance and assessing potential risk3.
Statistical pipe failure models provide a means of supporting proactive management, predicting future performance through discerning failure patterns from historical data and their contributory causal factors4. Shamir and Howard (1979)5 developed one of the first models on a small WDN of pipes, with a single-variate time-exponential model using pipe age to predict the number of failures per year per 1000 ft of pipe. Single-variate models are limited since multiple factors often operate concurrently to form complex mechanisms of failure that result in different modes of failure. These factors can be broadly categorised into pipe-intrinsic, environmental, and operational6. Further progress was made using multivariate models, including static (pipe and soil) and dynamic time-related variables (weather) to predict the number of failures or failure rates7, that can be used to rank pipes against each other8. Predicting the number of pipe failures at the asset level is mathematically problematic because incidents occur infrequently9. Therefore, studies based on failure rate focus on grouping pipe failures by similar characteristics across a network, providing enough failures by grouped pipe length for statistical significance10,11. However, grouping pipes at the network level makes assumptions that all pipes with similar characteristics share similar localised conditions (localised influences such as bedding conditions, traffic loading and local network jobs) and failure rates, which is rarely the case.
Deterministic models are often reported to be too simplistic, being unable to handle randomness or left-truncated data typically found in pipe failure data sets, which arise from missing failures due to limited short failure records12. Left-truncated data has the potential to mask pipes with high failure rates, and potentially reduce the accuracy of the final predictions. Furthermore, there is a need to predict failures at the pipe level to support effective management decision-making. Probability models such as survival analysis predict pipe failures at any phase in the life cycle13, consider the probability of random variables14, and accommodate left-truncated data addressed analytically through the adaption of the likelihood function15. Two widely used survival analysis models include the Proportional Hazard (PH) methods of Cox PH and the Weibull PH, demonstrating good predictive accuracy compared to deterministic models2,16. However, survival analysis is complex and only useful for long failure records, which many WDNs do not maintain17. Other probability models include the use of the probability distribution, such as logistic regression. Both Motiee and Ghasemnejad18 and Yamijala et al.19 considered multiple models, including Poisson, linear, exponential, and logistic modes developed to predict individual pipes. Both studies found logistic regression to provide the most useful results, since the probability of failure is often enough to inform management decisions and is more accurate than trying to predict the total number of failure at the pipe level, an approach where regression models have shown poor predictive accuracy3,17,18,19. However, imbalanced data still presents a problem that should be carefully considered20. Kleiner and Rajani21 conclude that in general, due to inherent uncertainty and lack of data, analysing the behaviour of a single pipe is unfeasible. Therefore, it seems sensible to group pipes, but at a lower spatial level than the entire network. Few studies to date have attempted this, with Chen et al.4 being a notable exception, grouping at the census level (homogeneous areas based on number of people with respect to population characteristics, with an optimum size of 4000 people22, leaving room for further exploration around grouping pipes at different levels.
Machine learning models are becoming more widely used in pipe failure modelling, and preferred since mathematical processing steps are unnecessary20, with complex data summarised in a way that improves prediction accuracy, and with the tuning of interaction terms offering greater flexibility than with traditional models11. Machine learning methods are data-driven, and the methods most suited to modelling pipe failures are supervised since they are considered grey box approaches, allowing a degree of flexibility and suitability for structured data23. Commonly used supervised machine learning methods include artificial neural networks, evolutionary polynomial regression, and support vector machines. However, machine learning models are computationally expensive, especially when tuning several hyperparameters and have a limited scope for interpreting casual relationships between the response variable and covariates24. Decision tree ensemble models overcome these limitations since they are more intuitive and transparent and can outperform other statistical methods. Studies have predominantly used Gradient Boosting Trees (GBT), which outperform other ensemble methods. Winkler et al.20, compared a Decision Tree, Random Forest, Adaboost and RUSboost model and found the RUSboost to have the highest accuracy (AUC of 0.93). Chen et al.4 compared a Gradient Boosting Model against a Generalised Linear Model, Generalised Additive Model, Random Forest and Generalised Linear Mixed Models (GLMM). The authors concluded that the gradient boosting model performs well returning the lowest Brier scores between 0.558 and 0.808. Giraldo-González and Rodríguez compared a Support Vector Machine, Artificial Neural Network, Bayes and Gradient Boosting model, and found the Gradient Boosting Model to perform best (AUC 0.998 for AC pipes and 0.990 for PVC pipes). These studies have typically focussed on five-year prediction intervals11,20, or short monthly prediction intervals4, yet some water network management decisions are performed annually, therefore it is sensible to understand the performance of GBT models on annual predictions.
For WDN managers, the concept of risk is important and yet often overlooked in pipe failure modelling25. Previous attempts to model risk include using the ranked ordered sorting of predictions based on the number of breaks8,26,27 or the probability of failure11,20. However, this approach is limited since water companies need to understand the risk of each potential failure as a combination of failure, either probability of failure or the number of failures, and the consequences. Christodoulou and Deligianni28 attempted to include a different risk level using proximity to buildings of public value and residential areas to prioritise repair and replacement work. Pietrucha-Urbanik and Tchórzewska-Cieślak29 proposed a framework for calculating the risk built on criteria grouping and weighting based on the potential financial losses arising. There are potentially numerous consequences of failures inherent to each network, yet common consequences include loss of water, potential disruption, reduction in water quality, reliability, direct costs (damage to property and infrastructure and pipe repair and replacement) and indirect costs (environmental and social). The risk of failure is complex, requiring several data sets from water companies and necessitates the difficult task of quantifying the consequences30. There is a gap in the literature in considering further developments in determining the risk of pipe failures.
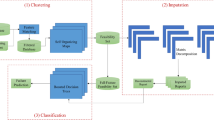
Although many studies compare multiple models, it is difficult to ascertain which is superior, since WDN data is variable across networks and geographical regions, which cannot be captured by the model. Instead, model performance relies on data quality, availability, and the model development31. Therefore, based on the gaps in the literature, this study aims to establish a reliable GBT prediction model for a UK WDN. The UK WDN has many of the typical issues that ageing infrastructure presents, which means most of the maintenance is performed reactively and wish to move towards proactively managing failures by predicting annual failures across the network. The WDN contains approximately 40,000 km of pipe covering some 27,476 km2 of an urban and rural environment, with a failure record history available over 14 years. The study will focus on the most commonly occurring pipe materials since the mechanism of failure has been established and can be accounted for by the variables used. The materials account for approximately 97 % of the UK WDN network, and include Iron, Steel and Ductile Iron (SDI), Asbestos Cement (AC), Polyvinyl Chloride (PVC) (collectively Unplasticised, Post Chlorinated and Molecular Orientated Polyvinyl Chloride) and Polyethylene (PE) (medium and high density). For shorter time intervals grouping pipes by similar characteristics is appropriate to yield more statistically accurate predictions, yet network wide groups are often unhelpful. This study uses a specific segmentation of pipes according to spatial characteristics and groups the segmented pipes by a 1 km interval. Using this 1 km interval is considered useful since it captures localised influences of weather and soil, removes the problem of grouping at larger spatial scale which often combines pipes with disparate failure rates, and presents smaller lengths of pipes and presents pipes with fewer failures, which is suitable for predicting the probability of failure. Previous studies have often limited failure models to predicting the probability of failure. Since the probability of failure alone is often not enough to support management decisions, this study builds on previous efforts by developing a practical approach to identify the risk of failure using weighted risk analysis.
Results and discussion
Receiver operator curve and area under the curve
The receiver operator curve (ROC) is used to visualise how the model performs independently of the decision threshold, providing a useful tool for visualising how well the classifier avoids false classifications32. The ROC plot shows a trade-off between the True Positive Rate (TPR) or sensitivity, the fraction of observations that are correctly classified, calculated in Eq. (1) as
where TP is True Positive and FN False Negative, and the False Positive Rates (FPR) or specificity, the fraction of observations that are incorrectly classified, calculated in Eq. (2) as
The passing of two lines corresponding to a 100% TPR and a 0% FPR = 1 (TPR versus 1−FPR) is considered a perfect discriminatory ability. This is graphically represented by the ROC curve passing the upper left-hand corner of the plot. The passing of the curve through the diagonal y = x represents a model that is no better than a random guess33. The Area Under the Curve (AUC) is an aggregated measure of performance for all classification thresholds and represents the measure of separability by describing the capability of the predictions in distinguishing between the classes. An AUC measure is returned between zero and one, with zero representing a perfectly inaccurate test and one a perfect test. In general, an AUC of 0.7 to 0.8 is considered acceptable, 0.8 to 0.9 is considered excellent, and >0.9 is outstanding34. Figure 1 shows the ROC curve for the test dataset close to the top left-hand corner and an AUC value of 0.89, suggesting the model has an excellent discriminative ability to distinguish between the classes, and the TPR and FPR appear robust enough to predict failures on the unseen test data.
The calibration curve provides a means of observing how close the predictions are to those observed. Since the outcome in this model is the probability of failure between 0 and 1, it is appropriate to use a binning method. Binning is advantageous since it averages the probability of failure for each bin which provides a useful graphical representation of how well the model is calibrated. The mean probability is then compared to the frequency of observed failures in each bin. In this case, a fixed-width binning approach is used, where the data is partitioned into ten bins known as decile analysis, and approach used in similar studies35. A reliability curve provides a means of visualising this comparison, whereby perfectly calibrated probabilities would lie on a diagonal line through the middle of the plot. The briers score is a useful measure of accuracy for probabilistic predictions and is equivalent to the mean squared error whereby the cost function minimises to zero for a perfect model and maximises to 1 for a model with no accuracy4. The Brier’s Score (BS) is calculated in Eq. (3) as
where N is the total number of observations, Pi is the prediction probability and Oi is equal to the event outcome failure or no failure. Figure 2 shows the calibration plot for the model and suggests the model is well calibrated for the lower and upper deciles since most bins fit the diagonal. The upper middle deciles do not fit the diagonal where the calibration curve is below or above the diagonal, suggesting the predictions have a lower probability than those seen in the data The briers score of 0.007 is low, suggesting accurate predictions overall.
Confusion matrix and accuracy
The confusion matrix describes the frequency of classification outcomes by explicitly defining the number of True Positives (TP, or Precision), True Negatives (TN), False Positives (FP), and False Negatives (FN). The decision to convert a predicted probability into a class label is determined by an optimal probability threshold such that the value of the response \(y_i = \left\{ {\begin{array}{*{20}{c}} {{\rm{no}}\,{\rm{failure}}\,{\rm{if}}\,P_i \le {\rm{threshold}}} \\ {{\rm{failure}}\,{\rm{if}}\,P_i > {\rm{threshold}}} \end{array}} \right.\). The default probability threshold within the model is 0.536. By this definition, there remains a practical need to optimise the probability threshold specifically to the behaviour of pipe failures within the imbalanced test data. An optimal probability threshold typically strikes a balance between sensitivity and specificity. However, there is a trade-off between TPR and FPR when altering the threshold, where increasing or decreasing the TPR typically results in the same for the FPR and vice versa. Probability threshold optimisation is an important step in the decision-making process and is specific to each problem. In the case of pipe replacement, expert judgement should be used by reasoning that water companies would seek to avoid unnecessarily replacing pipes that may have a longevity of several decades more, resulting in wasted maintenance effort and cost. Furthermore, only 0.5–1% of the network is typically replaced each year due to budget constraints37. It is therefore important to only identify pipes with the highest probability of failure. Considering this, the optimal threshold is set to reduce the FNs (i.e., pipes predicted to fail when they have not). This reduces the number of TPs predicted as discussed above but targets those pipes most likely to fail.
A factorial experimental design was used, whereby the threshold was iterated from 0.01 through to 0.99, observing each threshold to reveal the point where the highest accuracy meets the lowest FN value. The Matthews Correlation Coefficient (MCC) was used to measure accuracy and is useful for imbalanced data since it accounts for the difference in class size and only returns a high accuracy score if all four confusion matrix categories are accurately represented. For this reason, Chicco (2017) argues that it is the correct measure for imbalanced data sets. The MCC describes the prediction accuracy as worst value = −1 and best value = +1 and is calculated as shown in Eq. (4) as follows:
Table 1 shows a small range of the thresholds for brevity. The optimal threshold in this instance has been identified firstly with the highest MCC accuracy and then the lowest FN. The MCC of 0.27 suggests the model is better than a random fit, but a low MCC value also represents a high percentage of false positives (i.e., values incorrectly identified as non-failure). The balanced accuracy is also a good measure of the accuracy for imbalanced classes, where 1 is high and 0 is low. The balanced accuracy for this model is 0.65. In practical terms, the results are helpful for water companies to target areas for further investigation and potential replacement since they focus on those pipes having the highest probability of failure, yet there are still incorrect predictions that could lead to the potential replacement of pipes unnecessarily. The model predicts 20.20% of all failures occurring in the WDN, found in 7.83% of the WDN pipe network. The results show that approximately 32.80% of the observed pipe failures were correctly predicted as failures, whilst approximately 67.20% of the observed pipe failures were falsely predicted as no failure. If desired, water companies could choose an alternative threshold, one that eliminates FN predictions, however, the number of TP predictions will also reduce.
Relative variable influence
The relative variable influence shows the empirical improvement \(I_t^2\) accounted for by variable interval xj, averaged across all boosted trees as presented in Eq. (5) as follows38:
The variable influence helps understand which variables contribute more when predicting pipe failures. For GBT models, this is the summation of predictor influence accumulated over all the classifiers. Figure 3 shows the results, suggesting similar findings compared to existing literature. The most important variables are the number of previous failures and pipe length, both a proxy for pipe performance and deterioration. It is worth reiterating that both variables represent the grouped pipe and do not consider individual pipe history. Soil Moisture Deficit (SMD) is the most important weather variable being linked with shrinkage of clay soils and subsequent ground movement in AC pipe failures. Conversely, clay soils and soils shrink–swell potential, both representing ground movement, show lower influence.
Pipe diameter, and material are less important factors in this network than as reported in comparable studies11,20,21,39. The relative variable influence of days air frost and temperature is not as high as expected, given their correlation with high pipe failure frequency in iron pipes and the large percentage of iron pipes in the WDN. It is likely to be a result of over summarising the data to facilitate the annual prediction interval. A shorter prediction interval (week, or month) for networkwide groups of pipes is necessary to capture inter-annual variation accurately, but short prediction intervals in the authors’ experience can result in low predictive accuracy. The overall relative variable influence of soil (shrink well, soil corrosivity, Hydrology of Soil Type) is low. From literature and an engineering perspective, soil corrosion is strongly related to the deterioration of metal pipes and their ability to withstand internal and external forces3. It is possible that many pipes in this network may have been rehabilitated and protected against corrosion; however, this information was unavailable at the time of this study. Water source is the only operational variable and shows low influence compared to many other variables. The most important water source is surface water, resulting in lower temperatures during the winter due to its exposure to weather. This causes higher failure rates in metal pipes, yet compared to other variables, the influence is low. Other variables are imaginable such as installation details like bedding and backfill material, surrounding environments providing evidence on loading such as traffic loading and construction works, operational data such as pipe pressure and transients, water quality and spatial failure characteristics. These are not investigated here but will likely result in performance gains.
Risk mapping
For the mapping to be effective from an asset management standpoint, the results of the weighted risk analysis should be able to separate out low, medium, and high failures. The number of high failures is expected to be small for two reasons, (1) pipes rarely fail more than once and (2) utilities are only able to allocate investments to those at the greatest risk due to budget limitations and are therefore only interested in the top 1–2% of pipes. The outcome of the weighted risk analysis is presented in Fig. 4, representing a small section of the WDN for clarity. Natural Jenks arranges the risk level into three categories, low [0; ≤0.02], medium [>0.02; ≤0.06] and high [>0.06; ≤0.92]. In this scenario, the length of pipe in the high-risk category is 13.9 km of the 300.7 km or 4.6% of the pipe network present in Fig. 4, a useful percentage of the network to target for management decisions. The choropleth risk map approach is an important means of visualising individual pipes or clusters of pipes with the highest risk in the WDN, evidenced in Fig. 4. Figure 4 also highlights how many pipes in this section of the network have a low risk, which is to be expected since many pipes have a low probability of failure and have small diameters, potentially causing less damage if they fail.
Practical considerations
Creating groups of pipes was an important step given the low frequency of failures in the UK WDN dataset. Grouping pipes in this way assumes that all pipes in the group share similar failure rates, which is not the case, and thus the approach adopted here presents a suitable solution to this limitation. Grouping pipes on a lower spatial scale can capture localised influences on pipe performance, that can often be obfuscated when generalising over the whole network. However, the approach used may not be as useful for rural areas where fewer pipes are present, where smaller scales may be more appropriate (e.g., 1:100,000 is a smaller scale than 1:100). Further investigation into grouping scales is merited. Optimisation the threshold is challenging and inevitably leads to inappropriately classified failures on either side of the threshold. Optimising is even more difficult with imbalanced data sets since conventional classification methods are built to assume that all classes are equal. An alternative approach was applied in this study, which used MCC accuracy and FN to set a threshold, reducing the potential for wasting budgets replacing pipes that will not fail. In the process, the number of TPs was reduced to 32.80% of the observed pipe failures, whilst the number of FPs was 67.20% of the observed pipe failures, which may not present a good argument to professionals. Despite this, the results can be used directly in strategic planning, which sets long-term key decisions regarding maintenance and potential replacement of pipes. Predicting the probability of failure is an essential response since it enables the identification and prioritisation of risk across the network. This methodology could also be used to provide longer-term predictions to support the development of Asset Management Plan, which cover a five-year period of regulated investment.
Categorising the pipes based on a weighted risk analysis and visually presenting them using Natural Jenks offers a useful method for prioritising pipes based on the consequence of their failure and is an easily assessed cartographic presentation. It extends the probability of failure into a more useful measure of risk, providing more information for decision makers. The use of distance to property in this study is a simple approach to determine flooding. To provide a realistic determination of flooding, an understanding of key geographical features for overland flow routing is required40. The list of consequences was limited in this study and could be extended when such data is available. There are potentially numerous consequences of failure inherent to each network, yet common consequences include loss of water, potential disruption, reduction in water quality, reliability, direct costs (damage to property and infrastructure and pipe repair and replacement) and indirect costs (environmental and social)8. In this study, the risk estimates were concluded by expert knowledge, and any contextual mismatch between weightings could potentially skew the outcomes. Therefore, the weightings should be considered carefully by network professionals. At an engineering level, the risk mapping can be further used to determine areas of the network leading to a high probability of failure, which can be used to take constructive pre-emptive actions towards extending the life of future pipe construction41.
The economic benefits of this model will manifest when performing proactive maintenance, potentially averting associated risks that may arise from damaging properties and infrastructure. It is anticipated that the modelling approach proposed will enhance decision-making at a local level, facilitated through numerical outputs which report on the serviceability of the WDN and help meet regulatory performance targets avoiding heavy fines. Operationally, the approach will help with highlighting short pipe segments for repair and replacement though graphical outputs, these are practical lengths of pipes for operational teams that typically do not replace kms of pipe at any given time42. This approach shows similar performance to comparable GBT studies11,20, but is beneficial since the method provides reliable predictions on a shorter annual time frame. The method here is also computationally easier to develop than other more complex machine learning methods such as neural networks and Bayesian Neural Networks.
The predictions rely on the quality of the data, and several challenges were presented during the cleaning and processing, most notably the location of the pipe failures, many of which were geographically displaced, and some by a considerable distance yet was necessary to retain all the failures in the dataset. These were snapped to the nearest pipe with similar characteristics, yet it is conceivable that some were incorrectly placed despite the protocols established for the snapping process. Further limitations to the study include limited data, where pressure data or other operational data may have proved useful, the advantage of which may consist of increased model accuracy and interpretability. Over-summarised local conditions can also affect the model accuracy, and in this study, the local soil conditions were presented from a soil map at 1:250,000 scale. Likewise, the weather variables were highly summarised to an annual scale from a 40 × 40 km grid source. Inevitably these limitations will affect the model, which can potentially hinder effective decision-making. There are several challenges faced when modelling pipe failures, from uncertainties in data collection and management to specific data processing solutions. There is a need to understand these holistically, and from the view of current practice for a more in-depth perspective of current challenges in practice that may hinder useful data gathering. In addition, future research aimed at understanding how practitioners understand pipe failure models, the limitations, and opportunities is beneficial, since there is often a discord between the capabilities of modelling and user expectations. This further research may help to improve pipe failure models by encouraging enhancements in the pipe failure model process that promotes quality data capture.
Concluding remarks
This study considered the prediction of pipe failures using a GBT model and establishing the risk based on weighted risk analysis to prioritise pipes for proactive management. A 1 km spatial scale was included in this model when grouping the pipes, which aimed to capture localised conditions and remove the failure rate disparities shared when grouping pipes across a network. This spatial scale, together with a short prediction interval, the absence of some essential variables, and additional inherent problems with pipe failure data sets, has ultimately resulted in acceptable accuracy. However, in practical terms, when used in conjunction with expert knowledge, the results provide a useful approximation of potential failures and a better understanding of the current WDN to help plan rehabilitation and replacement efforts. Improving model accuracy may be achieved by increasing the prediction interval to five-year asset management plan, potentially accumulating more failures per pipe group from which to predict. Yet this may not be as useful to water companies where management decisions are typically annual. Furthermore, understanding the issues faced with data collection and quality from current practice may help to encourage data quantity and quality, and could potentially provide marked improvements in the final predictions.
Further suggested research includes exploring different pipe grouping variations, collecting more data on the consequences of failure to enhance the weighted risk analysis and, expanding on this idea, understanding the data quantity and quality issues from current practice, and exploring feature engineering techniques to derive more valuable data sets that may improve model accuracy.
Methods
Decision trees
The decision tree model is a machine learning method that is simple to implement, computationally efficient, and suitable for modelling complex relationships like those found in pipe failures20. A decision tree T partitions (or segments) the space of all explanatory variables into disjoint regions R1, R2, …, Rj through recursive partitioning along the axis (known as axis parallel partitions) using a top-down greedy approach to identify regions within regions based on the Gini index, a measure of total variance across the classes. The partitioning procedure continues until the stopping criterion is met, at which point the tree reaches the terminal node (the final space partitioned into non-overlapping regions). In this instance, the model describes the probability of failure via a Bernoulli distribution P(x,y), where one indicates a certain failure and zero no failure. All probabilities returned are within this [one-zero] interval. A decision tree is formally described in Eq. (6) as follows43:
where I is an indicator function, equal to 1 if the condition is true (failure) or 0 otherwise (non-failure). A constant cR is applied to each partitioned region that determines the probability in that region.
Decision trees are relatively simple to interpret and visualise (Fig. 5), can use multi-type variables, are not affected by variables on different scales, can accommodate missing variables and are insensitive to outliers. Yet decision trees model smooth functions poorly and can observe different partitions based on small changes to training data, introducing uncertainty, and resulting in poor predictions. It is therefore important to incorporate methods such as boosting to improve the predictions substantially.
(i) shows the two-dimensional data space. (ii) first condition for partitioning the data by variable x2 at 200, where disjoint region R1 is ≤200 and disjoint region R2 > 200. (iii) second condition for partitioning data by variable x1 at both 30 and 60 to create two more disjoint region R3 and R4 (Taken from Barton et al.55).
Gradient boosting
Using an ensemble of trees proves beneficial since the model learns slower and reduces overfitting variance and bias43. One such ensemble model is gradient boosting, a form of functional gradient descent, which describes a forward stage-wise procedure that fits multiple trees iteratively to the training data, aiming to minimise the loss function in the existing collection of trees by adding, at each step, another tree that best reduces the loss function. The loss function is a measure of how well the model coefficients fit the data, and in this study, the negative gradient of the deviance is used, which for classification models is the residual of the response minus the fitted probability mean, where \({{{\mathbf{r}}}} = {{{\mathbf{y}}}} - {{{\hat{\mathbf y}}}}\). The process is described by building a function\(\hat f_{{{\mathrm{B}}}}(x)\) which is the sum of the tree ensemble. The first tree is fitted with boosting iteration m1 to the training data and the response y, maximally reducing the loss function, from which the residuals are determined as \(r_1 = y_1 - \hat y_1\). Subsequent trees are fitted in the same way, but the following trees are updated based on the residuals of the previous trees such that \(r_i = r_{n - 1} - \hat r_{n - 1}\). Overfitting is avoided using regularisation applied as a shrinkage penalty factor of 0 < λ < 1 to scale the contribution of the tree. Regularisation through shrinkage offers a robust alternative to traditional variable selection methods such as stepwise variable selection24. Regularisation necessitates mutually. optimising the number of trees, learning rate and tree complexity. Another advantage of regularisation is that several covariates can be included in the model, and if they have a limited effect on the response, their contribution will simply be down weighted. This is easier than adding and removing variables to build a parsimonious model24. The shrunken tree is then added to the function: \(\hat f_{{{\mathrm{B}}}}\left( x \right) \leftarrow \hat f_{{{\mathrm{B}}}}\left( x \right) + \lambda\) T(x;γ) where x is the multivariate argument characterised by a set of parameters γ. The following trees with boosting iteration m2,m3,…, m are trained using the training data, and the residuals of each tree iteratively. Each tree is shrunken and successively added to the function, and the residuals updated so that \(r_i \leftarrow r_i - T(x;\gamma _b)\). The final regression gradient boosting model is depicted in Fig. 6 and the notation presented in Eq. (7) as follows43:
The process describes building the sum of the tree ensemble \(\hat f_{\mathrm{B}}(x)\), by fitting the boosted tree (T1, T2,...,Tn) iterations and maximally reducing the loss function from the residuals (Taken from Barton et al.55).
The gradient boosting model has many hyperparameters that control the execution of the learning. A sequential grid search across the different hyperparameters was undertaken to optimise the performance and to yield the best model. Each hyperparameter was tuned using an appropriate range, and the number of trees used in the boosting ensemble increased until the results no longer improved24. Five-fold cross-validation was used to balance the computational complexity of the model and its accuracy. The technique for K-fold cross-validation randomly partitions the training data into K equal subsamples, where a single subsample is retained for testing and the remaining subsamples are used for training24. The process is repeated K times so that each of the subsamples is used once as the testing subsample. Cross-validation calculates multiple estimates of ‘out of sample error’, returning the smallest to minimise overfitting43. R version 3.6.2 was used to develop the models44. The ‘gbm’ package version 2.8.145, and ‘caret’ package version 6.046 were both used from the CRAN repository.
Weighted risk analysis
There are several ways to determine risk29. In this study, risk R is a combination of the failure probability Pf and the sum of the consequences \(\mathop {\sum }\limits_i C_i^{{{\mathrm{f}}}}\), i.e., water loss (pipe diameter) and flooding damage (proximity to nearest property). The weighting is associated with the importance of each consequence. Since there is often more than one consequence, the consequences are summed and weighted by importance25. The final calculation is expressed in Eq. (8) as follows:
Table 2 shows the consequences, their weights and associated severity scores. The consequence score was determined by using four categories. The diameters were categorised according to diameter bands, and an assumed increase in water loss for larger diameters. The potential damage to property was determined in conjunction with expert knowledge, estimating that a pipe failure will likely cause more damage to closer properties. Given that approximately 71% of the network has a pipe diameter of <166 mm, catastrophic events and large volumes of water loss are unlikely; therefore, properties within 10 m are at highest risk.
Weighted risk analysis uses the probability of failure, the diameter size, and the pipe’s proximity to the nearest property since these were the only data available. The units determined for the consequence score were determined through dialogue with risk managers at UK water utility companies. The distance from the pipe to the nearest property was calculated using OS OpenMap buildings47 and the GIS package ArcGIS Pro48 to calculate the shortest planar distance between the pipe and the nearest property. The outcome of the weighted risk analysis is presented using Natural Jenks to arrange the data into three categories of risk, low, medium, and high. Natural Jenks is a clustering method that seeks to minimise the average deviation in each class based on natural groupings inherent in the data. Natural Jenks are advantageous since they identify real classes within the data and provide more meaningful visualisations49.
Data curation
The methods were applied to a UK WDN, operating over an area of approximately 27,476 km2 and supplying approximately 4.3 million people with drinking water. The UK WDN dataset includes failure records collected between 2005 and 2018, with information on pipe location, length, material type, age, diameter and water source, and failure location and time. The pipe failures collected on site were often geographically displaced from the pipe failure event. Therefore, all pipe failures were relocated to the nearest pipe to ensure no data was lost. Each pipe failure was firstly relocated within 3 m (a distance accounting for GPS error), and if no match was made, then the process was repeated sequentially up to 1 km until a pipe with equivalent characteristics of diameter and material type was found. Table 3 shows a summary of the WDN data.
Temperature and Soil Moisture Deficit (SMD) data were attained from the Met Office Rainfall and Evaporation Calculation System (MORECS 40 × 40 km grid) in a weekly summarised format. The total number of days air frost data were sourced from the Met Office summary data sets50, downloaded in a monthly summarised format. The soil data collected from the national soil map-related Natural Perils Directory and LandIS soil data and maps from Cranfield University51 are presented as 1:250,000 maps based on field data collected between 1939 and 1987. Using ArcGIS Pro, the pipe network data was segmented by the underlying soil characteristics, and the associated soil data attributed to the pipe segment. The MORECS and summary weather data were added to the dataset based on the 40 × 40 km MORECS grid value that was associated with the pipe using R software (version 4.0.0), and the pipe diameter and age were placed into categorised bands. The final covariates shown in Table 4 were selected based on available data and on those factors known to correlate with pipe failures, as discovered in complementary studies undertaken by the authors6,52.
The pipes are segmented and grouped based on similar characteristics, including material, diameter band, age band, soil characteristics, expressed in a 1 km grid to captured localised conditions, and remove the failure rate disparities shared when grouping pipes across a network. Each weather variable is summarised into extreme weather conditions (maximum and minimum values) and joined to the dataset. The final dataset contains 80,107 cohorts, with an average length of 433 m, a minimum length of 2 m and a maximum length of 11,995 m. The data is imbalanced, with one or more failures representing only 0.1%. Since the purpose is to predict the probability of pipe failure, which is typically enough information for decision makers, the number of failures are substituted for either failure or no failure. Some studies have separated material types into distinct data sets for modelling, since the mechanisms of failure are often unique to each material type. Yet here the data is used in a global model that included all materials, since several studies have suggested global models are the most suitable approach20,36,53 for three main reasons, (1) many variables are unavailable that are specifically unique to each material therefore most of the variables influence all materials, (2) the most unique aspect of the materials is the seasonal difference in failure rate, which, due to the annual predictions, is not included here, and (3) some materials such as SDI do not have enough pipe failures for good model convergence, yet through a global model this problem is removed by learning from a greater number of failures.
The data is partitioned into 70% training and 30% testing, a common approach for this type of study11,16,18, where large training datasets have shown improved model performance12. Randomly partitioning over the time frame is also useful since partitioning by year may introduce bias in the model in particularly extreme years (e.g. the hottest year on record)19,54. Stratified random sampling was used during the partition to ensure a representative sample of each material was included in both the training and testing dataset, such that: \(N = \mathop {\sum}\nolimits_{i = 1}^k {N_i,}\)where k are the number of strata (in this case the five materials) and Ni the number of sampling units in the ith strata.
Data availability
The authors do not have permission to share the network data due to its commercial nature. The weather and soil data that support the findings of this study are available, but restrictions apply to the availability of these data, which were used under licence for the current study, and are not publicly available. The weather data is available under licence from www.metoffice.gov.uk. The soil data used are available under licence from www.landis.org.uk. The OS OpenMap is available from the Ordnance Survey from https://www.ordnancesurvey.co.uk.
Code availability
The source code for the modelling has been provided in the Supplementary Material, Supplementary Methodology—R Markdown Model.
References
Ofwat. P. N. 22/18: Thames Water’s failure to tackle leakage results in £65m package for customers. (2020). Available at: https://www.ofwat.gov.uk/pn-22-18-thames-waters-failure-tackle-leakage-results-65m-package-customers/ (Accessed: June 2022).
Snider, B. & McBean, E. A. Improving urban water security through pipe-break prediction models: machine learning or survival analysis. J. Environ. Eng. 146, 04019129 (2019).
Tang, K., Parsons, D. J. & Jude, S. Comparison of automatic and guided learning for Bayesian networks to analyse pipe failures in the water distribution system. Reliab. Eng. Syst. Saf. 186, 24–36 (2019).
Chen, T. Y.-J., Beekman, J. A., David Guikema, S. & Shashaani, S. Statistical modeling in absence of system specific data: exploratory empirical analysis for prediction of water main breaks. J. Infrastruct. Syst. 25, 04019009 (2019).
Shamir, U. & Howard, C. D. D. An analytic approach to scheduling pipe replacement. J. Am. Water Works Assoc. 71, 248–258 (1979).
Barton, N. A., Farewell, T. S., Hallett, S. H. & Acland, T. F. Improving pipe failure predictions: factors affecting pipe failure in drinking water networks. Water Res. 164, 114926 (2019).
Kleiner, Y. & Rajani, B. Considering time-dependent factors in the statistical prediction of water main breaks. In: American Water Works Association Infrastructure Conference (AWWA 2000) 1–12 (2000).
Kakoudakis, K., Farmani, R. & Butler, D. Pipeline failure prediction in water distribution networks using weather conditions as explanatory factors. J. Hydroinformatics 20, 1191–1200 (2018).
Economou, T., Kapelan, Z. & Bailey, T. C. On the prediction of underground water pipe failures: zero inflation and pipe-specific effects. J. Hydroinformatics 14, 872–883 (2012).
Asnaashari, A., McBean, E. A., Shahrour, I. & Gharabaghi, B. Prediction of watermain failure frequencies using multiple and Poisson regression. Water Supply 9, 9–19 (2009).
Giraldo-González, M. M. & Rodríguez, J. P. Comparison of statistical and machine learning models for pipe failure modeling in water distribution networks. Water 12, 1153 (2020).
Snider, B. & McBean, E. A. Watermain breaks and data: the intricate relationship between data availability and accuracy of predictions. Urban Water J. 17, 163–176 (2020).
Wilson, D., Filion, Y. & Moore, I. State-of-the-art review of water pipe failure prediction models and applicability to large-diameter mains. Urban Water J. 14, 173–184 (2017).
St. Clair, A. M. & Sinha, S. State-of-the-technology review on water pipe condition, deterioration and failure rate prediction models! Urban Water J. 9, 85–112 (2012).
García, A. C., Solano, H., Gamiz, M. L. & Debón, A. Evaluation of the reliability of a water supply network from right-censored and left-truncated break data. Water Resour. Manag. 24, 2917–2935 (2010).
Kimutai, E., Betrie, G., Brander, R., Sadiq, R. & Tesfamariam, S. Comparison of statistical models for predicting pipe failures: illustrative example with the city of calgary water main failure. J. Pipeline Syst. Eng. Pract. 6, 04015005 (2015).
Chen, T. Y., Beekman, J. A. & Guikema, S. D. Drinking water distribution systems asset management: statistical modelling of pipe breaks. In (eds Pridmore, A. & Geisbush, J.) Pipelines. 173–186 ASCE: 2017.
Motiee, H. & Ghasemnejad, S. Prediction of pipe failure rate in Tehran water distribution networks by applying regression models. Water Supply 19, 695–702 (2019).
Yamijala, S., Guikema, S. D. & Brumbelow, K. Statistical models for the analysis of water distribution system pipe break data. Reliab. Eng. Syst. Saf. 94, 282–293 (2009).
Winkler, D., Haltmeier, M., Kleidorfer, M., Rauch, W. & Tscheikner-Gratl, F. Pipe failure modelling for water distribution networks using boosted decision trees. Struct. Infrastruct. Eng. 14, 1402–1411 (2018).
Kleiner, Y. & Rajani, B. Comparison of four models to rank failure likelihood of individual pipes. J. Hydroinformatics 14, 659–681 (2012).
United States Census Bureau. Glossary. (2021). Available at: https://www.census.gov/programs-surveys/geography/about/glossary.html. (Accessed: June 2022).
Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1, 206–215 (2019).
Elith, J., Leathwick, J. R. & Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 77, 802–813 (2008).
Suddle, S. The weighted risk analysis. Saf. Sci. 47, 668–679 (2009).
Chen, T. Y. J. & Guikema, S. D. Prediction of water main failures with the spatial clustering of breaks. Reliab. Eng. Syst. Saf. 203, 107108 (2020).
Berardi, L., Giustolisi, O., Kapelan, Z. & Savic, D. A. Development of pipe deterioration models for water distribution systems using EPR. J. Hydroinformatics 10, 113–126 (2008).
Christodoulou, S. & Deligianni, A. A Neurofuzzy decision framework for the management of water distribution networks. Water Resour. Manag. 24, 139–156 (2010).
Pietrucha-Urbanik, K. & Tchórzewska-Cieślak, B. Approaches to failure risk analysis of the water distribution network with regard to the safety of consumers. Water 10, 1679 (2018).
Farewell, T. S., Jude, S. & Pritchard, O. How the impacts of burst water mains are influenced by soil sand content. Nat. Hazards Earth Syst. Sci. 18, 2951–2968 (2018).
Kerwin, S., Garcia de Soto, B., Adey, B., Sampatakaki, K. & Heller, H. Combining recorded failures and expert opinion in the development of ANN pipe failure prediction models. Sustain. Resilient Infrastruct. 1–23. https://doi.org/10.1080/23789689.2020.1787033 (2020).
Saito, T. & Rehmsmeier, M. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 10, e0118432 (2015).
Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 27, 861–874 (2006).
Hosmer, D. W. & Lemeshow, S. Applied Logistic Regression (John Wiley & Sons, Inc., 2000). https://doi.org/10.1002/0471722146
Kumar, A. et al. Using machine learning to assess the risk of and prevent water main breaks. In: Proc. 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining 2657, 472–480 https://dl.acm.org/action/showFmPdf?doi=10.1145%2F3219819 (ACM, 2018).
Robles-Velasco, A., Cortés, P., Muñuzuri, J. & Onieva, L. Prediction of pipe failures in water supply networks using logistic regression and support vector classification. Reliab. Eng. Syst. Saf. 196, 106754 (2020).
Bruaset, S. & Sægrov, S. An analysis of the potential impact of climate change on the structural reliability of drinking water pipes in cold climate regions. Water (Switzerland) 10, 411 (2018).
Ridgeway, G. Generalized Boosted Models: A Guide to the gbm Package (CiteSeerX, 2019).
Konstantinou, C. & Stoianov, I. A comparative study of statistical and machine learning methods to infer causes of pipe breaks in water supply networks. Urban Water J. 17, 534–548 (2020).
Ozcelik, C. & Gorokhovich, Y. An overland flood model for geographical information systems. Water (Switzerland) 12, 2397 (2020).
Fitchett, J. C., Karadimitriou, K., West, Z. & Hughes, D. M. Machine learning for pipe condition assessments. J. Am. Water Works Assoc. 112, 50–55 (2020).
De Oliveira, D. P., Garrett, J. H. & Soibelman, L. A density-based spatial clustering approach for defining local indicators of drinking water distribution pipe breakage. Adv. Eng. Inform. 25, 380–389 (2011).
Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning. Springer Series in Statistics (Springer, 2009). https://doi.org/10.1007/978-0-387-84858-7.
R Core Team. R: The R Project for Statistical Computing. (2018). Available at: https://www.r-project.org/ (Accessed: February 2019).
Greenwell, B., Boehmke, B. & Cunningham, J. Package ‘gbm’—Generalized Boosted Regression Models. CRAN Repository 39 (2019).
Kuhn, M. et al. Package ‘ caret’—Classification and Regression Training. 1–223 (2020).
Ordnance Survey. OS OpenMap—Local. (2021). Available at: https://www.ordnancesurvey.co.uk/business-government/products/open-map-local. (Accessed: April 2021).
ESRI. ArcGIS Pro. (2021). Available at: https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview. (Accessed: February 2021).
North, M. A. A Method for implementing a statistically significant number of data classes in the Jenks algorithm. In: 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery 1, 35–38 https://dl.acm.org/doi/proceedings/10.5555/1674647 (IEEE, 2009).
Met Office. UK regional climate summaries 1981–2018. Met Office (2018). Available at: https://www.metoffice.gov.uk/research/climate/maps-and-data/regional-climates/index.
Hallett, S. H., Sakrabani, R., Keay, C. A. & Hannam, J. A. Developments in land information systems: examples demonstrating land resource management capabilities and options. Soil Use Manag. 33, 514–529 (2017).
Barton, N. A., Farewell, T. S. & Hallett, S. H. Using generalized additive models to investigate the environmental effects on pipe failure in clean water networks. npj Clean. Water 3, 31 (2020).
Jafar, R., Shahrour, I. & Juran, I. Application of Artificial Neural Networks (ANN) to model the failure of urban water mains. Math. Comput. Model. 51, 1170–1180 (2010).
Kabir, G., Tesfamariam, S., Loeppky, J. & Sadiq, R. Predicting water main failures: a Bayesian model updating approach. Knowl.-Based Syst. 110, 144–156 (2016).
Barton, N. A., Hallett, S. H., Jude, S. R. & Tran, T. H. An evolution of statistical pipe failure models for drinking water networks: a targeted review. Water Supply (2022). https://doi.org/10.2166/ws.2022.019.
Acknowledgements
This work was supported by the UK Natural Environment Research Council [NERC Ref: NE/M009009/1] and Anglian Water plc., who had no direct role in this study. The authors are grateful for their support.
Author information
Authors and Affiliations
Contributions
N.B.: conceptualisation, methodology, software, testing, formal analysis, investigation, resources, data curation, writing—original draft, writing—review and editing, visualisation and project administration. S.H.: Writing—review & editing, supervision, funding acquisition. S.J.: review & editing, supervision, funding acquisition. T.H.T.: Testing, formal analysis and review & editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethics declarations
The founding sponsors had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, and in the decision to publish the results.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barton, N.A., Hallett, S.H., Jude, S.R. et al. Predicting the risk of pipe failure using gradient boosted decision trees and weighted risk analysis. npj Clean Water 5, 22 (2022). https://doi.org/10.1038/s41545-022-00165-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41545-022-00165-2