Abstract
To provide a foundation for theoretical models of high-temperature superconductivity, experimental research has sought to establish correspondences between macroscopic transport coefficients on the one hand, and atomic-scale correlation functions measured by spectroscopic and scattering probes on the other hand. This research avenue has been confounded by the gradual onset of electronic ordering phenomena and of the corresponding transport anomalies. We report measurements of the uniaxial-stress dependence of the normal-state resistivity and Hall coefficient of the underdoped high-temperature superconductor YBa2Cu3O6.67. We observe a remarkable correspondence between the differential stress responses of the transport coefficients and resonant X-ray diffraction features indicative of charge ordering, which parallels the phenomenology of classical charge-density-wave compounds. However, our observations imply that static charge order is not responsible for a sign reversal of the Hall coefficient, and suggest that the interplay with liquid-like, dynamical charge correlations is essential for the prominent transport anomalies in the underdoped cuprates.
Similar content being viewed by others
Introduction
Nuclear magnetic resonance (NMR) and X-ray scattering experiments have recently identified charge order as a universal feature of the layered cuprates, and as the leading competitor of high-temperature superconductivity at moderate doping levels1,2,3. However, the fact that there is no sharply defined transition or onset temperature apparent in the thermal evolution of either direct measures of the charge order, or of any transport properties, makes it difficult to establish a correspondence between the two sets of observables. Recently, external control parameters have opened up fresh perspectives on this key issue. Specifically, the application of external magnetic fields of order 100 T has revealed a wealth of new information about quantum transport phenomena in the cuprates4,5,6,7,8,9, but the application of complementary spectroscopic and scattering probes under these extreme conditions remains a major challenge10,11,12,13. Hydrostatic pressure is another continuously tunable parameter, but corresponding studies have so far yielded seemingly contradictory results. Whereas X-ray scattering experiments indicate a complete suppression of charge order under modest pressure14, purported transport and NMR data signatures of charge order are only weakly pressure dependent15,16,17. However, the measurements were carried out on different samples and partly in high magnetic fields, which are known to enhance the charge ordering. In conjunction with the strong dependence of the doping level on hydrostatic pressure, these difficulties have so far precluded firm conclusions.
Recent experimental advances have enabled the application of highly homogeneous uniaxial stress to complex quantum materials, thereby opening up additional perspectives for in situ experiments with a continuously tunable parameter18,19,20,21,22,23,24,25,26,27,28. The application of stress in X-ray scattering experiments has already uncovered substantial modifications of the charge-ordered state of the cuprates29,30. However, transport measurements under high stress are difficult because even minor stress-induced cracks can disrupt the current flow. Despite the recent methodological progress, only few complementary studies on the stress response of transport coefficients in cuprates have been reported31. We report measurements of the stress dependence of the normal-state resistivity and Hall coefficient of twin-free single crystals of the underdoped high-Tc superconductor YBa2Cu3O6+x (YBCO6+x), which is particularly suitable for such experiments because of its low degree of lattice disorder (Fig. 1a). We chose the doping level of ~0.12 holes per copper ion (x = 0.67) where charge ordering is most pronounced32. A substantial stress-induced enhancement of the charge order was recently observed on crystals identical to those investigated here, using a nearly identical experimental setup29,30. We find remarkable parallels in the stress responses of the transport coefficients and the diffraction signal from static charge-ordering, especially with regard to their temperature evolution and in-plane anisotropy. This correspondence allows us to conclude that the condensation of collective charge fluctuations reduces the resistivity, similar to classical charge-density-wave (CDW) materials with quasi-two-dimensional (2D) electron systems, where this effect has been attributed to a loss of inelastic scattering channels in the CDW state33,34,35. However, we also conclude that the impact of static charge order is too weak to explain the most prominent transport anomalies, including the well-known sign reversal of the Hall coefficient as a function of temperature6. We argue that in YBCO6.67, liquid-like collective fluctuations of the electron system take on the role of static order in the classical CDW compounds, and we point out the need to develop a theoretical framework to describe the underlying mechanisms36. Our results illustrate the potential of uniaxial-pressure experiments with multiple complementary probes to elucidate the correspondence between atomic-scale electronic correlations and macroscopic transport phenomena in quantum materials.
a Unit cell of YBa2Cu3O761. Blue and red spheres represent Cu and O atoms, respectively. b Resistivity ρa in the absence of stress. c Schematic of the sample mounted on the uniaxial stress cell seen from the side (left). Top view of the stress cell (right). Sample platforms incorporated a mechanical contact are marked by red and green (Supplementary Note 2).
Results and discussion
Resistivity measurements
The single crystals of YBCO6.67 were grown using the flux method37. The oxygen content was controlled by annealing the samples at 555 \({^\circ\mathrm{C}}\) in a mixture of 5% O2 and 95% Ar for one week38. The samples were then detwinned mechanically39. The superconducting Tc = 65 K was determined by magnetometry (Supplementary Note 1), and the hole doping p ~ 0.12 was estimated from the c-axis lattice constant measured by X-ray diffraction at room temperature40. To maximize the homogeneity of the uniaxial stress, the samples were cut into rectangular blocks with typical dimensions ~2.5 mm × 0.2 mm × 0.1 mm41, and the stress was applied along the long axis. We studied two samples with long axes along the a-direction of the CuO2 layers (samples 1 and 3), and one sample (sample 2) with long axis along b, the direction of the CuO chains in the crystal structure (Fig. 1a). The resistivity ρ and Hall coefficient RH were measured in a standard four-probe configuration (see “Methods”). The temperature-dependent resistivity at ambient pressure measured in this way is consistent with prior reports, including signatures of pseudogap formation at temperatures around 200 K, well above the onset of charge order (Fig. 1b)42.
We pressurized the samples using a piezoelectric-based apparatus, illustrated in Fig. 1c, that incorporated sensors of both the force and displacement applied to the sample43,44,45. From the applied force, the stress in the sample can be accurately determined, independently of the deformation of the epoxy that holds the sample. Therefore, in the present study, we discuss the pressure effect in terms of stress (denoted as σxx and σyy for a and b-axis pressure, with negative sign for compressive stress). Additionally, in stress-sweep measurements, the samples were mounted onto platforms incorporating a mechanical contact that opens when the force falls to zero. This feature prevents the application of tensile stress, but allows accurate in situ calibration of the zero-force position (Supplementary Note 2). Note that the strain levels covered in the present study are below the onset strain of the three-dimensional (3D) charge order observed in recent X-ray scattering experiments29,30. Our study is thus limited to the possible influence of strain-enhanced 2D charge order on the transport coefficients.
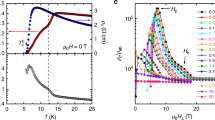
Figure 2 shows the normalized electrical resistance, ΔR/R, as a function of stress along the principal in-plane directions a and b for different temperatures. (Note that we plot the measured resistance rather than the resistivity because of the stress-dependent sample geometry, as discussed below.) Throughout the entire temperature range, ΔR/R shows a linear dependence on stress along both directions, but the amplitude and sign of the stress response evolve strongly with temperature. Figure 3a summarizes the temperature dependence of the stress response deduced from linear fits of the ΔR/R-versus-σ curves in Fig. 2. Since σ is negative throughout our study, we plot the stress derivative −d(ΔR/R)/dσ, which is positive (negative) if the resistivity increases (decreases) with increasing compression. Temperature sweep experiments of ΔR/R for fixed a-axis compression yield consistent results (sample 3 in Fig. 3a). The temperature dependence of −d(ΔR/R)/dσ is qualitatively similar for a- and b-axis compression, with a maximum at T ~ 150 K followed by a zero-crossing around 100 K. We, therefore, attribute this behavior to electrons in the CuO2 layers, rather than the CuO chains. However, we note that both the onset of the downturn and the zero-crossing are observed at higher temperature for stress along b, and that the amplitude of −d(ΔR/R)/dσyy at low T substantially exceeds the one of −d(ΔR/R)/dσxx (Fig. 3a).
a Stress response of the electrical resistance −d(ΔR/R)/dσ vs. temperature deduced from Fig. 2 (samples 1 and 2). Temperature sweep measurements at fixed stress are shown for an additional sample (sample 3). Here, the magnitude of ΔR/R was scaled by −1 GPa to convert the result to −d(ΔR/R)/dσ. The horizontal dashed line marks the geometric contribution to −d(ΔR/R)/dσ for ρ = constant (Supplementary Note 3). b Temperature dependence of the normalized intensity of the Bragg reflections characteristic of static charge-ordering measured by resonant X-ray scattering, reproduced from ref. 47. The vertical dashed line and shaded area mark the superconducting transition temperature Tc and the onset of static charge order TCO, respectively. Inset: Uniaxial stress dependence of the integrated peak intensity of both charge order domains with modulation propagating along the a- and b-directions, normalized to zero stress and summed together, extracted from the corresponding Bragg reflections30 (Supplementary Note 5).
In interpreting these results, we first consider the impact of stress on the sample geometry, which affects the measured resistance R = ρl/A via the length l and cross-sectional area A of the sample. Specifically,
where ρ is the resistivity, εxx = σxx/Ex is the strain (with the Young’s modulus Ex ~ 160 GPa), and (νxy, νxz) ~ (0.44, 0.16) are the Poisson’s ratios46. As 1 + νxy + νxz is positive, the geometric contribution to −d(ΔR/R)/dσ = −(1 + νxy + νxz)/Ex ~ −0.01 GPa−1, is negative and nearly temperature-independent at all temperatures, contrary to the measured pressure response (Fig. 3a and Supplementary Note 3).
Likewise, contributions to the intrinsic Δρ/ρ arising from the stress dependence of the electronic hopping parameters are expected to decrease monotonically with compression (see Supplementary Note 4 for corresponding tight-binding calculations). The strong, non-monotonic temperature dependence of the stress response at lower temperatures indicates many-body correlations of the electron system.
In view of the recent observation of strongly T-dependent incommensurate charge order by X-ray diffraction on samples of identical composition47, we compare our transport data to the amplitude of the diffraction signal arising from 2D charge order, which is displayed in Fig. 3b. We note that the onset of the downturn in −d(ΔR/R)/dσ (Fig. 3a) occurs just below the onset temperature of the charge order signal around TCO ~ 150–160 K. The in-plane anisotropies of the stress response of both quantities also exhibit striking similarities. Specifically, stress along both principal in-plane axes enhances the charge-ordering signal with an amplitude that is larger along b than along a (Fig. 3b)30, mirroring the amplitude and anisotropy of the stress response of the resistivity (Fig. 3a). These parallels suggest that the electrical resistivity is reduced by the onset of charge order. A similar effect has been observed in classical CDW compounds with 2D electron systems, where the CDW gap partially reconstructs the Fermi surface such that the impact of the reduced carrier density on the resistivity is over-compensated by the reduced scattering probability of the residual carriers34,35.
Hall effect measurements
In light of these considerations, we now discuss measurements of the Hall coefficient, which are displayed in Fig. 4. In agreement with prior work in the absence of pressure, the Hall coefficient, RH, is positive at high temperatures and exhibits a maximum on cooling below T ~ 150 K, followed by a zero-crossing at T0 ~ 70 K5,48. Based in part on quantum oscillation measurements in high magnetic fields, these phenomena have been ascribed to the formation of electron pockets via a Fermi surface reconstruction possibly induced by charge ordering, among other factors such as anisotropies of the Fermi surface and the scattering rate4,8,9. In qualitative agreement with this scenario, the application of stress amplifies the downturn of RH upon cooling below ~130 K (Fig. 4c), consistent with the stress-induced enhancement of the charge ordering amplitude inferred from X-ray diffraction30. The effect is again larger for stress along b than along a (Fig. 4c), mirroring the in-plane anisotropies of the longitudinal resistivity (Fig. 3a) and charge-ordering amplitude (Fig. 3b). On a qualitative level, our data thus provide additional implications of a Fermi-surface reconstruction induced by the experimentally observed charge correlations.
Temperature dependence of the Hall coefficient in a magnetic field of 8 T under uniaxial stress along the a-axis (panel a) and in 12 T and along the b-axis (panel b). The stress amplitudes are shown in the legend. Note that the upturn of RH upon cooling below ~40 K is due to the onset of superconductivity. c Difference between the Hall coefficients measured for σ ~ −1 GPa and σ = 0. d Sign reversal temperature T0 as a function of stress. The error bars are the standard deviations of T0.
However, we note a large quantitative disparity in the stress responses of the charge ordering amplitude and the transport coefficients. In particular, the intensity of the X-ray reflections increases by ~100% for a-axis compression by 1 GPa30, whereas only a small modification of RH and a ~1 K shift of T0 are observed under the same conditions (Fig. 4d). A related discrepancy was noted for hydrostatic pressure15,16, which appears to affect the manifestations of charge order in scattering experiments much more strongly than the corresponding transport features14. In the latter case, however, the association is complicated by the influence of hydrostatic pressure on the doping level, which varies strongly as a function of doping and may obscure the comparison of data on different samples17. Moreover, some of the transport experiments were conducted in high magnetic fields, which also affect the amplitude of the charge order. Uniaxial stress, on the other hand, does not affect the doping level. This is evidenced by the observation that a stress-induced suppression of charge ordering has not been observed—neither in YBCO6.67,29,30, which is at the top of the charge-ordering ‘dome’ in the phase diagram of the cuprates,3,32 nor in other YBCO6+x samples at higher or lower doping levels (data not shown). Moreover, our measurements were taken in modest magnetic fields and on samples prepared in an identical fashion, which can be compared without any ambiguity. The quantitative disparity between diffraction and transport signatures of charge order is, therefore, an intrinsic feature of YBCO6.67.
A possible solution to this conundrum is spatial inhomogeneity of the static charge order, which is indicated by the nonzero width of the diffraction features. X-ray scattering experiments with high energy resolution49 indicate that the X-ray reflections originate predominantly from charge ordered domains nucleated by residual disorder—a finding that is also supported by NMR results50. If these domains are spatially disconnected, the current flow detected in transport experiments may predominantly originate from regions with weak or absent static charge order, thus explaining the quantitative disparity between the stress responses of static charge order and transport.
However, these considerations also show that static charge order is not responsible for the most prominent anomalous transport features of YBCO6.67, including particularly the maximum and sign reversal of the Hall coefficient, which only depends weakly on stress (Fig. 4). In exploring alternative explanations, we can also rule out a Fermi-surface reconstruction by magnetic order, because static magnetism is not present in the YBCO system in the doping and magnetic-field range probed by our experiments. In principle, the unusual behavior of the Hall coefficient may arise from electronic correlations unrelated to density-wave order, including flux-flow phenomena in a phase-incoherent superconducting state that precedes superconducting long-range order. This scenario was invoked early on51 to explain the sign reversal of RH, but subsequent experiments have called this interpretation into question, based in part on the observed magnetic field independence of T0, and on the continuous evolution of the low-field Hall coefficient into the quantum-oscillation regime that indicates a reconstructed Fermi surface in high magnetic fields48. Moreover, recent theoretical work indicates that phase-incoherent Cooper pairing does not reverse the sign of RH52. Finally, we note that the superconducting transition temperature decreases (increases) under a-axis (b-axis) compression45. The stark contrast of this asymmetric strain response to the symmetric response of the normal-state resistivity and Hall effect is inconsistent with a major influence of superconductivity on the phenomena we have observed.
Conventional CDW order can thus be ruled out as the main origin of the transport anomalies, and one may ask whether slowly fluctuating, dynamical charge correlations recently uncovered by resonant inelastic X-ray scattering (RIXS)3,53,54,55,56 offer an alternative explanation. These correlations grow strongly upon cooling, suggesting a critical divergence that is only cut off by the onset of superconductivity. Two factors argue in favor of such a scenario. First, the temperature evolution of the dynamical correlations is closely similar to that of the static order. Indeed, the diffraction features in elastic X-ray scattering can be understood as a ‘central peak’ resulting from pinning of low-energy collective charge fluctuations by defects49. The analogy between the T-evolution of charge order and transport coefficients pointed out above, therefore, also holds for dynamical correlations. Second, in contrast to the (slightly broadened) Bragg reflections manifesting static order, the dynamical charge correlations exhibit a ring-like pattern in reciprocal space57, akin to analogous patterns in quantum spin liquids and superfluid helium. (Note that the ring pattern has thus far only been observed in Bi-based cuprates, but is also expected in YBCO6.67 in view of the universality of the charge correlations in the cuprates3.) Such liquid-like correlations (as well as the associated transport anomalies) are less directional in real space, and are hence expected to be less susceptible to stress along particular lattice directions than the static order. In a strongly fluctuating system, however, even a small stress-induced spectral-weight shift of the fluctuation spectrum may induce a large fractional response of the elastic ‘tail’ due to pinned fluctuations. This scenario can thus explain the quantitative disparity between the transport and diffraction features.
In summary, our investigation of the stress dependence of the resistivity and Hall coefficient of YBCO6.67 has demonstrated surprising qualitative analogies to classical CDW materials with 2D electron systems, where the loss of scattering channels in the CDW state lowers the resistivity. Interestingly, the long-range-ordered ‘striped’ state in the La2−xBaxCuO4 family leads to an increase of the resistivity at the onset of charge order58, possibly due to the influence of concomitant magnetic and lattice instabilities. In this context, we point out that the strain levels covered by our transport measurements were insufficient to reach the recently discovered state with 3D charge order in YBCO29. However, the momentum-integrated intensity of the X-ray diffraction features of 2D charge order largely exceeds the one of the 3D charge order (see Supplementary Note 5). Although these considerations suggest a dominant role of 2D charge order even at high strain levels, direct transport measurements in this regime are an interesting subject of future research.
Our data suggest a key role of liquid-like, nearly critical charge correlations for fermionic transport, in contrast to the electron–phonon-interaction driven static charge order in the classical systems. There have been a number of theoretical proposals along these lines, but few explicit calculations of transport coefficients. Calculations of the Hall coefficient in the framework of models with slowly fluctuating charge36 or spin59 order indicate a subtle downturn at low temperatures, but a sign reversal has not been predicted to the best of our knowledge. The concrete link between transport and scattering probes of charge correlations uncovered in our parametric study should motivate further progress in the development of this theoretical framework, for instance, by including the interplay with pairing fluctuations. On the experimental front, our study has demonstrated the power of uniaxial-pressure experiments in the long-standing quest to establish correspondences between atomic-scale correlations and macroscopic transport in high-Tc superconductors. Extending this approach to other spectroscopic probes and other collective phenomena will open up new perspectives for quantum materials research.
Methods
Transport measurements
Electrical contacts were prepared by sputtering Au on the surface60. Electrical resistivity (ρ) measurements were carried out along the stress direction by a standard ac lock-in method with a driving current of frequency ~80 Hz. Samples 1 and 3 (sample 2) thus yielded ρa (ρb) (Supplementary Note 6). Hall coefficient (RH) measurements were carried out with magnetic field along the c-axis for samples 2 and 3. The measurements were performed with both positive and negative fields, to eliminate the contribution of the longitudinal magnetoresistivity.
Data availability
Data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Wu, T. et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat. Commun. 4, 2113 (2013).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 337, 821–825 (2012).
Frano, A., Blanco-Canosa, S., Keimer, B. & Birgeneau, R. J. Charge ordering in superconducting copper oxides. J. Phys.: Condens. Matter 32, 374005 (2020).
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565–568 (2007).
LeBoeuf, D. et al. Electron pockets in the Fermi surface of hole-doped high-Tc superconductors. Nature 450, 533–536 (2007).
Proust, C. & Taillefer, L. The remarkable underlying ground states of cuprate superconductors. Annu. Rev. Condens. Matter Phys. 10, 409–429 (2019).
Sebastian, S. E. et al. Metal-insulator quantum critical point beneath the high Tc superconducting dome. Proc. Natl Acad. Sci. USA 107, 6175–6179 (2010).
Harrison, N. & Sebastian, S. E. Fermi surface reconstruction from bilayer charge ordering in the underdoped high temperature superconductor YBa2Cu3O6+x. N. J. Phys. 14, 095023 (2012).
Sebastian, S. E. & Proust, C. Quantum oscillations in hole-doped cuprates. Annu. Rev. Condens. Matter Phys. 6, 411–430 (2015).
Chang, J. et al. Magnetic field controlled charge density wave coupling in underdoped YBa2Cu3O6+x. Nat. Commun. 7, 11494 (2016).
Gerber, S. et al. Three-dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science 350, 949–952 (2015).
Jang, H. et al. Coincident onset of charge-density-wave order at a quantum critical point in underdoped YBa2Cu3Ox. Phys. Rev. B 97, 224513 (2018).
Lee, W.-S. X-ray studies of the CDW ground state and excitations in high-TC cuprates. J. Phys. Soc. Jpn. 90, 111004 (2021).
Souliou, S. M. et al. Rapid suppression of the charge density wave in YBa2Cu3O6.6 under hydrostatic pressure. Phys. Rev. B 97, 020503 (2018).
Putzke, C. et al. Charge order and superconductivity in underdoped YBa2Cu3O7−δ under pressure. Phys. Rev. Lett. 120, 117002 (2018).
Cyr-Choinière, O. et al. Sensitivity of Tc to pressure and magnetic field in the cuprate superconductor YBa2Cu3Oy: evidence of charge-order suppression by pressure. Phys. Rev. B 98, 064513 (2018).
Vinograd, I. et al. Nuclear magnetic resonance study of charge density waves under hydrostatic pressure in YBa2Cu3Oy. Phys. Rev. B 100, 094502 (2019).
Hicks, C. W. et al. Strong increase of Tc of Sr2RuO4 under both tensile and compressive strain. Science 344, 283–285 (2014).
Steppke, A. et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 355, eaaf9398 (2017).
Barber, M. E., Gibbs, A. S., Maeno, Y., Mackenzie, A. P. & Hicks, C. W. Resistivity in the vicinity of a van Hove singularity: Sr2RuO4 under uniaxial pressure. Phys. Rev. Lett. 120, 076602 (2018).
Pfau, H. et al. Anisotropic quasiparticle coherence in nematic BaFe2As2 studied with strain-dependent ARPES. Phys. Rev. B 103, 165136 (2021).
Grinenko, V. et al. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 17, 748–754 (2021).
Li, Y. S., Borth, R., Hicks, C. W., Mackenzie, A. P. & Nicklas, M. Heat-capacity measurements under uniaxial pressure using a piezo-driven device. Rev. Sci. Instrum. 91, 103903 (2020).
Ikeda, M. et al. Elastocaloric signature of nematic fluctuations. Proc. Natl Acad. Sci. USA 118, e2105911118 (2021).
Watson, C. A., Gibbs, A. S., Mackenzie, A. P., Hicks, C. W. & Moler, K. A. Micron-scale measurements of low anisotropic strain response of local Tc in Sr2RuO4. Phys. Rev. B 98, 094521 (2018).
Pustogow, A. et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature 574, 72–75 (2019).
Ghosh, S. et al. Piezoelectric-driven uniaxial pressure cell for muon spin relaxation and neutron scattering experiments. Rev. Sci. Instrum. 91, 103902 (2020).
Qian, T. et al. Apparatus design for measuring of the strain dependence of the seebeck coefficient of single crystals. Rev. Sci. Instrum. 91, 023902 (2020).
Kim, H.-H. et al. Uniaxial pressure control of competing orders in a high-temperature superconductor. Science 362, 1040–1044 (2018).
Kim, H.-H. et al. Charge density waves in YBa2Cu3O6.67 probed by resonant X-ray scattering under uniaxial compression. Phys. Rev. Lett. 126, 037002 (2021).
Ishida, K. et al. Divergent nematic susceptibility near the pseudogap critical point in a cuprate superconductor. J. Phys. Soc. Jpn. 89, 064707 (2020).
Blanco-Canosa, S. et al. Resonant X-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x. Phys. Rev. B 90, 054513 (2014).
Harper, J. M. E., Geballe, T. H. & DiSalvo, F. J. Thermal properties of layered transition-metal dichalcogenides at charge-density-wave transitions. Phys. Rev. B 15, 2943–2951 (1977).
Monceau, P. Electronic crystals: an experimental overview. Adv. Phys. 61, 325–581 (2012).
Zhu, X., Guo, J., Zhang, J. & Plummer, E. W. Misconceptions associated with the origin of charge density waves. Adv. Phys.: X 2, 622–640 (2017).
Caprara, S., Di Castro, C., Seibold, G. & Grilli, M. Dynamical charge density waves rule the phase diagram of cuprates. Phys. Rev. B 95, 224511 (2017).
Lin, C. T., Zhou, W., Liang, W. Y., Schönherr, E. & Bender, H. Growth of large and untwinned single crystals of YBCO. Physica C 195, 291–300 (1992).
Lindemer, T. B. et al. Experimental and thermodynamic study of nonstoichiometry in YBa2Cu3O7−x. J. Am. Ceram. Soc. 72, 1775–1788 (1989).
Lin, C. & Kulakov, A. In situ observation of ferroelastic detwinning of YBCO single crystals by high temperature optical microscopy. Physica C 408, 27–29 (2004).
Liang, R., Bonn, D. A. & Hardy, W. N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys. Rev. B 73, 180505 (2006).
Hicks, C. W., Barber, M. E., Edkins, S. D., Brodsky, D. O. & Mackenzie, A. P. Piezoelectric-based apparatus for strain tuning. Rev. Sci. Instrum. 85, 065003 (2014).
Ando, Y., Komiya, S., Segawa, K., Ono, S. & Kurita, Y. Electronic phase diagram of high-Tc cuprate superconductors from a mapping of the in-plane resistivity curvature. Phys. Rev. Lett. 93, 267001 (2004).
Barber, M. E., Steppke, A., Mackenzie, A. P. & Hicks, C. W. Piezoelectric-based uniaxial pressure cell with integrated force and displacement sensors. Rev. Sci. Instrum. 90, 023904 (2019).
Barber, M. E. et al. Role of correlations in determining the Van Hove strain in Sr2RuO4. Phys. Rev. B 100, 245139 (2019).
Barber, M. E. et al. Dependence of Tc of YBa2Cu3O6.67 on in-plane uniaxial stress. Phys. Rev. B 106, 184516 (2022).
Lei, M. et al. Elastic constants of a monocrystal of superconducting YBa2Cu3O7-δ. Phys. Rev. B 47, 6154–6156 (1993).
Achkar, A. J. et al. Distinct charge orders in the planes and chains of ortho-III-ordered YBa2Cu3O6+δ superconductors identified by resonant elastic X-ray scattering. Phys. Rev. Lett. 109, 167001 (2012).
LeBoeuf, D. et al. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field Hall effect measurements. Phys. Rev. B 83, 054506 (2011).
Le Tacon, M. et al. Inelastic X-ray scattering in YBa2Cu3O6.6 reveals giant phonon anomalies and elastic central peak due to charge-density-wave formation. Nat. Phys. 10, 52–58 (2014).
Wu, T. et al. Incipient charge order observed by NMR in the normal state of YBa2Cu3Oy. Nat. Commun. 6, 6438 (2015).
Harris, J. M. et al. Additive quasiparticle and vortex Hall conductivities in La2−xSrxCuO4 and untwinned YBa2Cu3O6.93. Phys. Rev. B 51, 12053–12056 (1995).
Boyack, R., Wang, X., Chen, Q. & Levin, K. Combined effects of pairing fluctuations and a pseudogap in the cuprate Hall coefficient. Phys. Rev. B 99, 134504 (2019).
da Silva Neto, E. H. et al. Coupling between dynamic magnetic and charge-order correlations in the cuprate superconductor Nd2−xCexCuO4. Phys. Rev. B 98, 161114 (2018).
Miao, H. et al. Formation of incommensurate charge density waves in cuprates. Phys. Rev. X 9, 031042 (2019).
Yu, B. et al. Unusual dynamic charge correlations in simple-tetragonal HgBa2CuO4+δ. Phys. Rev. X 10, 021059 (2020).
Huang, H. Y. et al. Quantum fluctuations of charge order induce phonon softening in a superconducting cuprate. Phys. Rev. X 11, 041038 (2021).
Boschini, F. et al. Dynamic electron correlations with charge order wavelength along all directions in the copper oxide plane. Nat. Commun. 12, 597 (2021).
Li, Q., Hücker, M., Gu, G. D., Tsvelik, A. M. & Tranquada, J. M. Two-dimensional superconducting fluctuations in stripe-ordered La1.875Ba0.125CuO4. Phys. Rev. Lett. 99, 067001 (2007).
Storey, J. G. Hall effect and Fermi surface reconstruction via electron pockets in the high-Tc cuprates. Europhys. Lett. 113, 27003 (2016).
Ekin, J. W. et al. High Tc superconductor/noble-metal contacts with surface resistivities in the 10−10 Ωcm2 range. Appl. Phys. Lett. 52, 1819–1821 (1988).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
Self-flux growth was performed by the Scientific Facility ‘Crystal Growth’ at Max Planck Institute for Solid State Research, Stuttgart, Germany.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.N., P.Y., M.E.B., and K.I. performed the transport measurements. S.N. analyzed the data. S.N., H.-H.K., and T.L. prepared the single crystals studied in the present work. The uniaxial stress devices were built by P.Y., M.E.B., and C.W.H. B.K., M.L.T., M.M., C.W.H., and A.P.M. supervised the project. S.N., M.M., and B.K. wrote the manuscript with suggestions from all coauthors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nakata, S., Yang, P., Barber, M.E. et al. Normal-state charge transport in YBa2Cu3O6.67 under uniaxial stress. npj Quantum Mater. 7, 118 (2022). https://doi.org/10.1038/s41535-022-00532-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00532-9