Abstract
The anomalous Hall effect (AHE), typically observed in ferromagnetic (FM) metals with broken time-reversal symmetry, depends on electronic and magnetic properties. In Co3Sn2-xInxS2, a giant AHE has been attributed to Berry curvature associated with the FM Weyl semimetal phase, yet recent studies report complicated magnetism. We use neutron scattering to determine the spin dynamics and structures as a function of x and provide a microscopic understanding of the AHE and magnetism interplay. Spin gap and stiffness indicate a contribution from Weyl fermions consistent with the AHE. The magnetic structure evolves from c-axis ferromagnetism at \(x = 0\) to a canted antiferromagnetic (AFM) structure with reduced c-axis moment and in-plane AFM order at \(x = 0.12\) and further reduced c-axis FM moment at \(x = 0.3\). Since noncollinear spins can induce non-zero Berry curvature in real space acting as a fictitious magnetic field, our results revealed another AHE contribution, establishing the impact of magnetism on transport.
Similar content being viewed by others
Introduction
The concept of topology has been predicted and experimentally identified amongst materials with little or no electron correlations and is arguably a success in the pursuit of materials by design1,2. In contrast, topology in strongly correlated materials is much less explored due to a lack of identified material platforms and the difficulty in developing theories that incorporate topology and electron correlations. The role of magnetism in topologically protected states has implications for both our fundamental understanding of properties and the technological applications of quantum materials such as dissipationless spintronics3,4. The magnetic semimetal Co3Sn2S2 is particularly interesting because the interplay between magnetism and topology leads to giant anomalous Hall effect (AHE), where charge carriers acquire a velocity component orthogonal to an applied electric field without an external magnetic field, with a small ordered moment5,6. Remarkably, the size of AHE in Co3Sn2S2 is among the largest compared to most previously reported AHE materials5. The magnetic Co ions in Co3Sn2S2 form a two-dimensional (2D) kagome lattice, composed of corner sharing triangles and hexagons, separated by nonmagnetic S and Sn layers with another Sn intercalated between the Co-S layer (Fig. 1a). Depending on the nature of the magnetic order, the observed AHE may have different microscopic interpretations7,8,9,10,11,12. If Co3Sn2S2 is a simple half-metallic ferromagnet below \(T_C = 177\) K with Co moment aligned along the c-axis as predicted by ab initio calculations, the spin-orbit coupling (SOC) would induce a splitting of the electronic bands and open up gaps with the anti-crossing nodal line connected to the Weyl points5,6,13,14,15,16,17. In this case, the intrinsic AHE in Co3Sn2S2 arises from Berry curvature of the pairs of Weyl points characterized by the opposite chiralities acting as the monopole and anti-monopole of the emergent magnetic field in momentum space. However, if the magnetic structure has an additional in-plane 120° antiferromagnetic (AFM) order component with one basis vector (termed \(\psi _1\)) below ~90 K as suggested by muon-spin rotation (μSR) measurements [the red arrows in Fig. 1b]11, the numbers of Weyl nodes and their locations in reciprocal space will change considerably, thus giving rise to different emergent magnetic field, Berry curvature, and intrinsic AHE. Although recent polarized neutron diffraction experiments on Co3Sn2S2 ruled out the \(\psi _1\) AFM order proposed in Ref. 11. a different in-plane 120° AFM order with two basis vectors as shown in blue arrows of Fig. 1b (\(\psi _2\)) is still possible though not confirmed12.
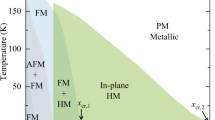
a Crystal structure of Co3Sn2S2 from a three-dimensional view. b Top view with the in-plane symmetry-allowed spin configurations \(\psi _1\)and \(\psi _2\). c–d Brillouin zone boundaries and high-symmetry points in a c three-dimensional and d two-dimensional view. e Out-of-plane and f in-plane magnetization as a function of doping in zero and low field. (g) Indium doping dependence of the anomalous Hall conductivity based on19. h Temperature-doping phase diagram. Dots indicate temperature and doping of neutron experiments. i–j In-plane and out-of-plane components of the refined magnetic structures at x = i 0.0 and j 0.12 and 0.3.
One way to resolve the magnetic structure of Co3Sn2S2 is to carry out systematic neutron scattering experiments as a function of chemical doping and compare the outcome with AHE measurements. By partially substituting Sn with In to form Co3Sn2-xInxS2, the system changes from an FM Weyl semimetal to a nonmagnetic insulator18. While the low-temperature magnetization of the system decreases monotonically with increasing In-doping, the AHE enhances significantly near x = 0.15 and decreases until vanishing at x > 0.819. This non-monotonic doping dependence of the intrinsic anomalous Hall conductivity in Co3Sn2-xInxS2 has been attributed to doped induced changes in Berry curvature near the Fermi level19. On the other hand, much is unknown about the evolution of the magnetic structure of this system. For example, magnetic, transport, and optical measurements on Co3Sn2S2 reveal a clear anomaly around 120 K well below TC = 177 K11,15,16,20. Although previous neutron scattering experiments could not rule out the \(\psi _2\) AFM order, a sudden reduction in FM domain size is believed to be responsible for the observed properties below 120 K12.
In this paper, we report neutron scattering experiments to determine the evolution of spin dynamics and magnetic structures in Co3Sn2-xInxS2 as a function of x that provide a microscopic understanding of the doping and temperature dependent AHE. We find that the magnon gap due to SOC and in-plane spin stiffness exhibits a non-monotonous temperature dependence that follows the enhanced AHE as a function of temperature and In-doping. Additionally, we determine the evolution of the magnetic structure as a function of temperature and In-doping x. With increasing x, the magnetic structure changes from a simple ferromagnet with moment along the c-axis at x = 0 to a canted AFM structure with reduced c-axis FM moment and an in-plane 120° AFM order with two basis vectors at x = 0.12. The AFM moment increases while the FM moment decreases with increasing doping until magnetism disappears at x = 1. Since noncollinear spin texture can induce non-zero Berry curvature which acts as an effective magnetic field to the conduction electrons21,22,23, our results suggest that there is an additional contribution to the AHE, thus establishing the basis for a comprehensive understanding of AHE in these materials.
Results
Preliminary characterization
Large single crystals of Co3Sn2-xInxS2 with x = 0, 0.12, 0.3 were grown using a flux method24. Their compositions were confirmed using powder X-ray diffraction and Inductively Coupled Plasma Optical Emission Spectroscopy at Rice University (see Methods Section for details). Neutron diffraction measurements were performed on single crystals with x = 0.12, 0.3 using the elastic diffuse scattering spectrometer CORELLI at the Spallation Neutron Source (SNS) and the WAND2 diffractometer of the High Flux Isotope Reactor both at Oak Ridge National Laboratory (ORNL)25,26. Co3Sn2-xInxS2 crystallizes in a rhombohedral structure (space group: R\(\bar 3\)m) with Co atoms that form kagome layers in the ab-plane (Fig. 1a). The corresponding Brillouin zone is shown in Fig. 1c,d. We define the momentum transfer Q in 3D reciprocal space in \({\AA}^{ - 1}\) as Q = Ha*+Kb*+Lc*, where H, K, and L are Miller indices and a* = 2π (b × c)/[a·(b × c)], b* = 2π (c × a)/[a·(b × c)], c* = 2π (a × b)/[a·(b × c)] with \(a = a\hat x\), \(b = a(\cos 120\hat x + \sin 120\hat y)\), \(c = c\hat z\) (a = b ~ 5.36, c ~ 13.14 Å) (Fig. 1a–d).
Figures 1e and 1f show the temperature dependence of the c-axis and in-plane magnetization, respectively, for x = 0.12, 0.3. The applied field is 0.1 T, slightly lower than the 0.5 T field used in Ref. 19. While the overall In-doping dependent data is consistent with Ref. 19. we find a clear reduction in the c-axis field magnetic magnetization below 50 K for x = 0.12, suggesting the presence of a AFM component. The signature of FM domain size reduction, seen most clearly as a kink in the in-plane field magnetization data below ~120 K for x = 012, is confirmed for x = 0.12, 0.3 single crystals (Fig. 1f).
Figure 1g and h summarizes the In-doped dependence of the AHE and its comparison with the magnetic structures of the system obtained from our transport and neutron scattering experiments and Ref. 19. Assuming Co3Sn2S2 is a simple ferromagnet with c-axis aligned moment (Fig. 1i), increasing In-doping to x = 0.12 changes the magnetic structure to canted antiferromagnet with c-axis moment and in-plane \(\psi _2\) AFM order (Fig. 1j). Upon further increasing In-doping to x = 0.3, the FM component along the c-axis decreases and the in-plane AFM moment increases while maintaining the same AFM structure (Fig. 1j).
Neutron diffraction
For each doping level on CORELLI, a single crystal of 10–30 mg was mounted on an aluminum pin and aligned in the [H,0,L] scattering plane. The crystal was rotated through 360 degrees to cover a large area of reciprocal space. For x = 0.12, full maps were collected at 6 (Fig. 2a), 60, and 165 K (Fig. 2b). For x = 0.3, full maps of neutron intensities were collected at 6 and 160 K. The data were reduced using MANTID27 to extract nuclear and magnetic Bragg peak intensities. The nuclear and magnetic structure refinements were then carried out using Jana2006 software28. Figure 2a, b shows reciprocal space maps in the [H,0,L] scattering plane for the x = 0.12 at T = 6 and 165 K obtained on CORELLI. From susceptibility measurements shown in Fig. 1e and f, we know that the FM component of the magnetization decreases below around 50 K, in addition to changes in FM domain around 120 K. Figure 2c shows the temperature dependence of the (1,0,1) magnetic Bragg peak for the x = 0.12 sample. Below TC = 165 K, the intensity of the (1,0,1) peak increases with decreasing temperature showing no anomaly around 120 K and reaches a maximum near 50 K before sharply decreasing upon further decreasing temperature. This decrease indicates a deviation from normal FM behavior and an increase in the in-plane AFM component in the magnetic structure.
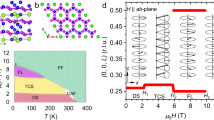
Maps of magnetic peaks in reciprocal space from neutron diffraction of x = 0.12 sample at (a) 6 K and (b) 165 K. c Temperature dependence of the (1,0,1) magnetic Bragg peak intensity. Refined magnetic structures in x = 0.12 crystals at (d) 6 K and (e) 60 K and (f) x = 0.3 at 6 K. Comparison of measured (Fobs) and calculated (Fcalc) integrated intensities from the refinement in the \(\psi _2 + \psi _3\) magnetically ordered phases shown in (d–f) in x = 0.12 crystals at (g) T = 6 K and (h) 60 K and (i) x = 0.3 at 6 K. The overall R values= 3.79, 3.63, and 4.04% for x = 0.12 at (g) T = 6 K, (h) 60 K, and (i) x = 0.3 at 6 K, respectively. The overall R values best fit the data for the \(\psi _2 + \psi _3\) structure compared to the \(\psi _1 + \psi _3\) structure where overall R = 4.70, 4.58, and 5.50% for x = 0.12 at (g) T = 6 K, (h) 60 K, and (i) x = 0.3 at 6 K, respectively.
From the full reciprocal space map at 165 K (T > TC), the crystal lattice structure was refined and used as the input for the magnetic refinement. We consider the symmetry allowed magnetic structures compatible with the magnetic Co atom positions and k = 0 propagation vector as there are no new superlattice peaks appearing below TC. The possible Irreducible representations (Γ) and associated basis vectors (ψ) are detailed in the Methods Section. At T = 60 K (>TN), the magnetic structure can be well refined assuming a simple c-axis aligned FM (\(\psi _3\) of Γ2+) (Fig. 2e). On cooling to temperatures below 50 K, when the system has an additional AFM component, we can refine the magnetic structure assuming coexistence of a c-axis aligned FM moment with the \(\psi _1\) or \(\psi _2\) in-plane AFM structure. Both configurations have 120-degree, in-plane AFM moments with \(\psi _1\) moments along (a,a,0), (-a,0,0), and (0,-a,0) and while \(\psi _2\) has moments along (a,-a,0), (a,2a,0), and (-2a,-a,0). Consistent with Ref. 12. we find that the \(\psi _1 + \psi _3\) magnetic structure cannot best explain the data. On the other hand, the \(\psi _2 + \psi _3\) magnetic structure with \(\varphi = 25^\circ\) gives a satisfactory refinement to the data, forming a canted AFM or umbrella-like structure with components along both the c-axis and in-plane, \(\psi _2\) AFM order (Fig. 2d, g). As ψ2 is part of Γ2+, this canting is allowed within the original magnetic structure without invoking any additional symmetry breaking.
For x = 0.3, the nuclear structure at 160 K was refined and used as an input for the magnetic structure refinement at 6 K. The refinement calculated intensities fit well with the measured intensities as shown in Fig. 2i. Our refinements indicate that the best fit to the data is again the \(\psi _2 + \psi _3\)magnetic structure but with \(\varphi = 65^\circ\) at 6 K [Fig. 2i]. Therefore, we conclude that as In-doping is increased from 0 to 0.3, the low temperature magnetic structure evolves from a simple FM phase in the parent compound to a canted FM with components along both the c-axis and in-plane AFM order, where the AFM moment size increases with In-doping at the expense of the FM moment. In-doping introduces holes to the system and slightly increases the separation of kagome layers which may explain why this system disfavors FM arrangement with increased doping11,29.
Magnetization and transport measurements
From the magnetic susceptibility (Fig. 1e) and order parameter measurements (Fig. 2c), we see that the non-collinear canted spin structure only appears below about 50 K in the x = 0.12 sample. Since the \(\psi _2 + \psi _3\) magnetic structure is noncollinear and has non-zero spin chirality [\(\chi = {{{\boldsymbol{S}}}}_i \cdot ({{{\boldsymbol{S}}}}_j \times {{{\boldsymbol{S}}}}_k)\, \ne\, 0\), where \({{{\boldsymbol{S}}}}_i\), \({{{\boldsymbol{S}}}}_j\), \({{{\boldsymbol{S}}}}_k\) are the three nearest spins], it can induce non-zero Berry curvature acting as effective magnetic field for the conduction electrons giving rise to the topological Hall effect (THE)30,31,32,33. Recent neutron diffraction work on YMn6Sn6 showed field-induced non-collinear spin can indeed induce THE34,35,36. To test if this is also the case for Co3Sn2-xInxS2, we carried out c-axis magnetic field dependence of the Hall resistivity for x = 0.12 and 0.3 samples (Fig. 3a, b)19. The magnetization measurements for these samples are shown in Fig. 1e with anomalous low temperature behavior in the x = 0.12 sample. We clearly see a similar behavior in the anomalous Hall conductivity (AHC) \(\sigma _{xy}\left( T \right)\) for the x = 0.12 sample in Fig. 3c. We compare the AHC and magnetization of the x = 0.12 sample in Fig. 3d and observe a slight decrease followed by an increase in AHC below 50 K despite a monotonic decrease in magnetization. Therefore, the enhanced AHC at low temperature must be due to an additional mechanism such as non-zero spin chirality. We attribute this low temperature effect to the THE whose presence is in addition to AHE due to net magnetization which are proportional to \(a\rho _{xx}M + b\rho _{xx}^2M\). In Fig. 3e, we show the anomalous Hall resistivity and the results are fit to the THE fit due to the net magnetization as discussed above in Fig. 3f. In the x = 0.12 sample, we see an extra contribution that we attribute to THE due to the spin-chirality of the refined magnetic structure as indicated by the shaded region where an approximately 10% deviation is observed. This 10% deviation corresponds to a 3.5 µΩ cm topological resistivity, which is comparable to the size of THE in other well know non-colinear antiferromagnets such as Mn3Sn37 and Nd2Mo2O738.
Field dependence of \(\rho _{xy}\) for (a) x = 0.12 and (b) x = 0.3. c Temperature dependence of the anomalous Hall conductivity. d Anomalous Hall conductivity compared to order parameter of (1,0,1) magnetic peak. e Temperature dependence of the anomalous Hall resistivity. f Anomalous Hall resistivity compared fit to the expected contributions from intrinsic and extrinsic scattering mechanisms. Deviations at low temperature in the x = 0.12 sample (shaded in blue) indicate a possible topological Hall contribution due to non-zero spin chirality.
Inelastic neutron scattering
Having determined the magnetic structure of Co3Sn2-xInxS2, we now consider the effect of spin dynamics to the AHE39,40,41. In previous work on Weyl semimetal candidate SrRuO3, the observed non-monotonic temperature dependence of the AHC \(\sigma _{xy}\left( T \right)\), induced by Berry curvatures near Weyl points, is associated with temperature dependence of the spin gap \(E_g\left( T \right)\) in FM spin waves via:
where M(T) and M0 are the magnetization at temperature T and saturation moment, respectively; ag and b are nearly temperature independent constants, and \(\sigma _0\) is a normalization factor which can be related to lattice parameter of the system41. Similarly, the spin wave stiffness \(D_H\left( T \right)\) has a large temperature dependence that follows:
where \(a_D\) is a near temperature independent constant. The same temperature dependence of the AHE (b) is used to describe the stiffness softening, consistent with previous analyses in9,41.
For Co3Sn2S2, inelastic neutron scattering experiments confirm the strong interplay between spin dynamics and AHC9,10. To test what happens in Co3Sn2-xInxS2, we measured the in-plane spin wave dispersion around (0,0,3) in x = 0.12 sample. Inelastic neutron scattering measurements were performed on single crystals with x = 0.12 using the IN-8 and Thales triple-axis spectrometers at the Institut Laue-Langevin (ILL) in Grenoble, France42,43. We used doubly focusing pyrolytic graphite monochromator and analyzer with PG(0,0,2) reflection. Several scans were performed with a Cu(200)/PG(004) configuration. About 40 individual single crystals were co-aligned on an aluminum plate to form an assembly with a mosaic spread of 2 deg. The crystal assembly oriented in the [H, 0, L] horizontal scattering plane.
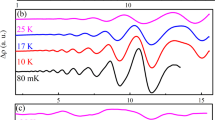
Figure 4a shows several constant-Q scans at (0,0,3), revealing clear spin gap at different temperatures. The spin gap was determined by fitting each curve to an ex-Gaussian function (detailed in the Methods Section). The resulting temperature dependence of the spin gap is shown in Fig. 4b where the blue dashed line represents the fit of Eq. (1) with \(a_g = 3.65\) meV and b = 0.60 compared to the black dashed line with \(a_g = 2.36\) meV and b = 0.0 whose fitting is worse than with non-zero b. Therefore, like in the parent compound, the temperature dependence of the AHE and therefore non-zero b must be included to best fit the data. We compare the magnitude of b to that reported for the parent compound where b=0.39, indicating a strong interplay between the Weyl topology and spin dynamics with increased In doping9.
a Select energy dependence of the spin excitations at T = 35, 110, 155, and 165 K (see supplementary information for fit details). b Temperature dependence of the spin wave gap and fitting results with different parameters with TC = 165 K. c Dispersion curve of the spin wave excitations along [H,0,3] at 5 and 200 K fit to a q2-dependence and compared to x = 0 data from9 as shown in square points. After data analysis9, claims a gapless spectrum at 200 K. d Temperature dependence of the in-plane spin-wave stiffness DH and fitting results with different parameters and TC = 165 K. DH was determined using fixed Eg determined from energy scans (Fig. 4a) and then fitting the dispersions along H (Fig. 4c). The vertical error bars in (a) are statistical errors of 1 standard deviation. The horizontal and vertical error bars in (b–d) represent the estimated uncertainty obtained in fitting procedures.
Figure 4c shows the in-plane spin wave dispersions at 5 K and 200 K compared to the parent compound results of ref. 9. The temperature dependences of spin wave stiffness were obtained by fitting the spin wave dispersion with \(E \approx E_g\left( T \right) + D_H\left( T \right)q^2\) where E is energy of spin waves, Eg was fixed based on the ex-Gaussian fit results, and q the momentum transfer away from the zone center. The resulting temperature dependence is shown in Fig. 4d. The black and blue dashed lines are fits of the \(D_H\left( T \right)\) by Eq. (2) with zero and finite b, respectively. Although finite b fits the data slightly better, the differences with zero b is not large.
Discussion
In a recent μSR study, the temperature and In-doping dependent magnetic phase diagram of Co3Sn2-xInxS2 was reported29. The FM ground state at x=0.0 transitions into mixed FM+AFM state around 5 and 15% of In-doping, and then becomes FM+helimagnetic (HM) state for doping between 15 to 30%, and finally changes to HM state for x≥0.30. The outcome from our neutron diffraction results indicates that the phase diagram of Co3Sn2-xInxS2 is much simpler, showing only the FM+AFM phase with \(\psi _2\) magnetic structure. The effect of In-doping is to transform c axis FM order into in-plane AFM order. The fact that x = 0.12 sample has AFM order appearing well below the FM ordering temperature provided a natural interpretation of the temperature dependent AHE, suggesting the presence of THE from noncollinear spin structure contribution. These results, together with inelastic scattering measurements, clarified the phase diagram of the system, and provided the basis to understand the interplay between magnetism and topological magnetic properties.
In summary, we have used neutron diffraction to map out the In-doping evolution of the magnetic structures of Co3Sn2-xInxS2. We show that the parent compound is a pure ferromagnet with moment along the c axis and \(T_C = 177\) K. Around \(x = 0.12\), the system is still a ferromagnet below 165 K, but an in-plane AFM order with \(\psi _2\) magnetic structure sets in at \(T_N = 50\) K, forming a FM+AFM (\(\psi _2 + \psi _3\)) magnetic structure that induced a THE effect consistent with transport measurements. Finally, on moving to \(x = 0.3\), AFM component increases at the expense of FM component, but the magnetic structure is still FM+AFM with \(\psi _2 + \psi _3\) structure. Our inelastic neutron scattering experiments on \(x = 0.12\) reveal that spin dynamics in the doped compound behave similarly as the undoped Co3Sn2S2 where the magnon gap due to SOC and in-plane spin stiffness are renormalized by the same factor consistent with the AHE. The appearance of AFM order with noncollinear structure clearly affects the observed AHE. These results thus established the magnetic structures of the system from which a future microscopic theory for the AHE and THE can be established.
Methods
Sample synthesis
Single crystals of Co3Sn2-xInxS2 (\(0 \le x \le 0.3\)) were grown by an Sn/In self flux method21. Initial compositions with the molar ratio Co:S:Sn/In = 8:6:86 were used. Co, Sn, S, and In powders were mixed together and placed in the bottom of an Al2O3 crucible. The top of the crucible was filled with quartz wool. The crucible was sealed in an evacuated quartz tube and placed in a box furnace. The mixture was heated to 400 °C over 2 h, held for 2 h, heated to 1050 °C over 6 h, held for 6 h, and them cooled slowly to 700 °C over 100–150 h. The tube was removed from the furnace and spun in a centrifuge to remove flux. Plate-like crystals with hexagonal shape were obtained.
Chemical composition
The chemical composition of synthesized crystals was measured by X-ray diffraction (XRD) and Inductively Coupled Plasma Optical Emission Spectroscopy chemical analysis both at Rice University. Powder XRD measurements were performed on crushed single using a Rigaku Smartlab II X-ray Diffractometer to confirm the 322-phase. The In composition was determined using a Perkin Elmer Optima 8300 Inductively Coupled Plasma Optical Emission Spectrometer (ICP-OES) at Rice University. By comparing the ratio of Co:In in dissolved samples, an average doping level of x = 0.12. was found over four samples from four different batches with xnom = 0.15. Similar analysis found x = 0.3 for batches with xnom = 0.4.
Magnetization measurements
The field-cooled (FC) temperature dependent magnetization data was fit to a power law function to extract the value of TC excluding the low temperature data in x = 0.12 data. Then including all data, an additional fit to a polynomial function was used to fully capture the measured temperature dependence and compared to the temperature dependence of energy gap and in-plane dispersion (Figs. 4b and 4d in the main text). An example of temperature dependent magnetization is shown in Supplementary Fig. 1 for x = 0.3 sample. Here we compare zero-field cooled (ZFC) and FC data and clearly see the domain size transition TD near 120 K.
Measurements were done to confirm the In-doping level by comparing to previous studies of the doping dependence of \(T_C\) by19. Based on those previous results, \(T_C\) follows a doping dependence approximately described by the function \(T_C = - 59.51 \ast x^2 - 134.1 \ast x + 182.1\) as shown in Supplementary Fig. 2. Using this function to compare \(T_C\) in our samples indicated doping levels of x = 0.12 and x = 0.3. These levels are consistent with our ICP-OES results. Additionally, the magnitude of the anomalous Hall conductivity observed in19 are consistent with our results.
Transport measurements
Transport measurements were performed on samples polished and cut to a bar shape. Silver paste and gold wires were used to make resistivity measurements in a Hall bar geometry as shown in Supplementary Fig. 3a-b. Temperature dependent resistivity measurements are shown in Supplementary Fig. 4 as a function of temperature. The temperature dependences of anomalous Hall resistivity and conductivity were fit to a polynomial function and compared to the temperature dependence of energy gap, in-plane dispersion, and anomalous Hall resistivity. Temperature dependence of the percent deviation between the fit and measured anomalous Hall resistivity is shown in Supplementary Fig. 5.
Elastic neutron scattering
Our elastic neutron scattering experiments were carried out at CORELLI at the Spallation Neutron Source (SNS) and WAND2 at the High Flux Isotope Reactor (HFIR) at Oak Ridge National Laboratory (ORNL), Oak Ridge, TN, USA25,41. For each experiment and sample doping level, a single crystal of 10-50 mg was mounted in the [H,0,L] scattering plane at CORELLI and [H,-H,0] scattering plane at WAND2. The crystals were put in a closed cycle refrigerator and rotated 360 degrees to collect large reciprocal space maps as a function of temperature. The Mantid package was used for data reduction and analysis. Jana2006 software was used for structure refinement. Nuclear refinements were done using peak intensities from the 165 K, x = 0.12 and 160 K, x = 0.3. A total of 304 and 150 reflections, respectively, were used in the refinement and resulted in good fits with R values of 3.02 and 4.55%. These nuclear refinements were used as inputs for the magnetic refinements at 6 and 60 K for x = 0.12 and 6 K for x = 0.3. For x = 0.12 6 K, 408 reflections were used and resulted in an R value of 3.80%. For x = 0.12 60 K, 369 reflections were used and resulted in an R value of 3.63%. For x = 0.3 6 K, 168 reflections were used and resulted in an R value of 4.04%.
Representation analysis
Based on the magnetic Co sublattice and the k = 0 propagation vector, there are nine possible magnetic configurations as shown in Table 1. The nine basis vectors, \(\psi _{1 - 9}\), are categorized into three irreducible representations (irreps) labeled by \({{\Gamma }}_{1 - 3}^ +\). The moment direction are relative magnitude are M(x,y,z).
Inelastic neutron scattering
Inelastic neutron scattering measurements were performed on single crystals with \(x = 0.12\) using the IN-8 and Thales spectrometers at the Institut Laue-Langevin (ILL) in Grenoble, France. We used doubly focusing pyrolytic graphite monochromator and analyzer with PG(0,0,2) reflection. Several scans have been performed with a Cu(200)/PG(004) configuration. For these experiments, ~1 g of x = 0.12 crystals were coaligned in the [H,0,L] scattering plane and fixed to an Al plate as shown in Supplementary Fig. 6.
The temperature dependence of the energy gap was measured by performing constant-Q cuts from 0 to 5 meV. To extract the energy gap, each leading-edge peak was fit to an exponentially modified Gaussian distribution, a convolution of a Gaussian and exponential distribution, where the exponential distribution accounts for the asymmetric tail that results from finite resolution. The exponentially modified Gaussian distribution can be written as, \(f\left( x \right) = \frac{\lambda }{2}e^{\frac{\lambda }{2}(2\mu + \lambda \sigma ^2 - 2x)}erfc^{\frac{{\mu + \lambda \sigma ^2 - x}}{{\sqrt 2 \sigma }}}\), with parameters (\(\lambda ,\sigma ,\mu\)) where \(\lambda\) is a constant, \(\sigma\) is the standard deviation of the Gaussian, and \(\mu\) is the mean of the Gaussian. For each temperature (See Supplementary Fig. 7a), this function was fit to the data (See Supplementary Fig. 7b) and the peak position was extracted as the energy gap (Eg) as summarized in Table 2.
Constant energy scans were performed along [0,0,L] and [H,0,3] as a function of temperature. Several scans are shown in Supplementary Fig. 8. For each scan, data were fit to a double Gaussian function including two slightly asymmetric peaks as
for H-scans and
for L-scans after subtracting a linear background. At each temperature, energy versus \(\pm \delta\) was fit to the function \(E = E_g + Dq^2\) using the measured values of \(E_g\) to determine the spin stiffness D.
Data availability
The data supporting the findings of this study are available within the paper and in the Supplementary Information. The raw data are available from the corresponding authors upon reasonable request. The raw data obtained on IN8 and Thales at ILL are available at https://doi.org/10.5291/ILL-DATA.4-01-1630. The raw data from CORELLI and the WAND2 diffractometers are available upon request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Wang, Q. H. et al. The magnetic genome of two-dimensional van der Waals materials. ACS Nano 16, 6960–7079 (2022).
Lv, B. Q., Qian, T. & Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 93, 025002 (2021).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).
Ghimire, M. P. et al. Creating Weyl nodes and controlling their energy by magnetization rotation. Phys. Rev. Res. 1, 032044 (2019).
Yang, R. et al. Magnetization-induced band shift in ferromagnetic Weyl semimetal Co3Sn2S2. Phys. Rev. Lett. 124, 077403 (2020).
Liu, C. et al. Spin excitations and spin wave gap in the ferromagnetic Weyl semimetal Co3Sn2S2. Sci. China.: Phys. Mech. Astron. 64, 217062 (2021).
Zhang, Q. et al. Unusual exchange couplings and intermediate temperature Weyl state in Co3Sn2S2. Phys. Rev. Lett. 127, 117201 (2021).
Guguchia, Z. et al. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 11, 559 (2020).
Soh, J.-R. et al. Magnetic structure of the topological semimetal Co3Sn2S2. Phys. Rev. B 105, 094435 (2022).
Xu, Y. et al. Electronic correlations and flattened band in magnetic Weyl semimetal candidate Co3Sn2S2. Nat. Commun. 11, 3985 (2020).
Liu, D. F. et al. Direct observation of the spin–orbit coupling effect in magnetic Weyl semimetal Co3Sn2S2. npj Quantum Mater. 7, 11 (2022).
Okamura, Y. et al. Giant magneto-optical responses in magnetic Weyl semimetal Co3Sn2S2. Nat. Commun. 11, 4619 (2020).
Xu, Q. et al. Topological surface Fermi arcs in the magnetic Weyl semimetal Co3Sn2S2. Phys. Rev. B 97, 235416 (2018).
Schnelle, W. et al. Ferromagnetic ordering and half-metallic state of Sn2Co3S2 with the shandite-type structure. Phys. Rev. B 88, 144404 (2013).
Corps, J. et al. Interplay of metal-atom ordering, Fermi level tuning, and thermoelectric properties in cobalt shandites Co3M2S2 (M = Sn, In). Chem. Mater. 27, 3946–3956 (2015).
Zhou, H. et al. Enhanced anomalous Hall effect in the magnetic topological semimetal Co3Sn2-xInxS2. Phys. Rev. B 101, 125121 (2020).
Lachman, E. et al. Exchange biased anomalous Hall effect driven by frustration in a magnetic kagome lattice. Nat. Commun. 11, 560 (2020).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Denisov, K. S., Rozhansky, I. V., Averkiev, N. S. & Lähderanta, A. General theory of the topological Hall effect in systems with chiral spin textures. Phys. Rev. B 98, 195439 (2018).
Kassem, M. A., Tabata, Y., Waki, T. & Nakamura, H. Single crystal growth and characterization of kagomé-lattice shandites Co3Sn2−xInxS2. J. Cryst. Growth 426, 208–213 (2015).
Ye, F., Liu, Y., Whitfield, R., Osborn, R. & Rosenkranz, S. Implementation of cross correlation for energy discrimination on the time-of-flight spectrometer CORELLI. J. Appl. Cryst. 51, 315–322 (2018).
Frontzek, M. D. et al. WAND2—A versatile wide angle neutron powder/single crystal diffractometer. Rev. Sci. Instrum. 89, 092801 (2018).
Arnold, O. et al. Mantid—Data analysis and visualization package for neutron scattering and μ SR experiments”. Nucl. Instrum. Methods Phys. Res. A. 764, 156–166 (2014).
Petříček, V., Dušek, M. & Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallog. 229, 345–352 (2014).
Guguchia, Z. et al. Multiple quantum phase transitions of different nature in the topological kagome magnet Co3Sn2−xInxS2. npj Quantum Mater. 6, 50 (2021).
Ueda, K. et al. Topological Hall effect in pyrochlore lattice with varying density of spin chirality. Phys. Rev. Lett. 108, 156601 (2012).
Ueland, B. G. et al. Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal. Nat. Commun. 3, 1067 (2012).
Bruno, P., Dugaev, V. K. & Taillefumier, M. Topological Hall effect and Berry phase in magnetic nanostructures”. Phys. Rev. Lett. 93, 096806 (2004).
Metalidis, G. & Bruno, P. Topological Hall effect studied in simple models. Phys. Rev. B 74, 045327 (2006).
Wang, Q. et al. Field-induced topological Hall effect and double-fan spin structure with a c-axis component in the metallic kagome antiferromagnetic compound YMn6Sn6. Phys. Rev. B 103, 014416 (2021).
Ghimire, N. J. et al. Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6. Sci. Adv. 6, eabe2680 (2020).
Dally, R. L. et al. Chiral properties of the zero-field spiral state and field-induced magnetic phases of the itinerant kagome metal YMn6Sn6. Phys. Rev. B 103, 094413 (2021).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N. & Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 291, 2573–2576 (2001).
Onoda, M., Mishchenko, A. S. & Nagaosa, N. Left-handed spin wave excitation in ferromagnet. J. Phys. Soc. Jpn. 77, 013702 (2008).
Itoh, S. et al. Weyl fermions and spin dynamics of metallic ferromagnet SrRuO3. Nat. Commun. 7, 11788 (2016).
Jenni, K. et al. Interplay of electronic and spin degrees in ferromagnetic SrRuO3: Anomalous softening of the magnon gap and stiffness. Phys. Rev. Lett. 123, 017202 (2019).
Boehm, M. et al. ThALES—Three axis low energy spectroscopy for highly correlated electron systems. Neutron N. 26, 18–21 (2015).
Hiess, A. et al. ILL’s renewed thermal three-axis spectrometer IN8: A review of its first three years on duty. Phys. B: Condens. Matter 385-386, 1077–1079 (2006).
Acknowledgements
We wish to thank Ursula Bengaard Hansen and Paul Steffens for help and assistance for the Thales experiment. The neutron scattering and single crystal synthesis work at Rice is supported by US NSF-DMR-2100741 and by the Robert A. Welch Foundation under Grant No. C-1839, respectively (P.D.). The transport measurements at UW were supported by the Air Force Office of Scientific Research (AFOSR) under Award No. FA2386-21-1-4060 and the David Lucile Packard Foundation (J.H.C). A portion of this research used resources at the Spallation Neutron Source and the High Flux Isotope Reactor, a DOE Office of Science User Facility operated by ORNL.
Author information
Authors and Affiliations
Contributions
P.D. and J.-H.C. conceived and managed the project. The single-crystal Co3Sn2-xInxS2 samples were grown by K.J.N. and B.G. Neutron diffraction experiments at CORELLI and the WAND2 diffractometers were performed by K.J.N., F.Y. and K.M.T. Neutron refinements were carried out by K.J.N. in discussion with F.Y. Inelastic neutron scattering experiments at IN-8 and Thales spectrometers were performed by P.B. and A.I. in discussion with P.D. and K.J.N. Magnetic susceptibility measurements were performed by K.J.N. Transport measurements were carried out by Y.S., P.M. and J.-H.C. The paper is written by K.J.N., P.D., J.-H.C., and all co-authors made comments on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neubauer, K.J., Ye, F., Shi, Y. et al. Spin structure and dynamics of the topological semimetal Co3Sn2-xInxS2. npj Quantum Mater. 7, 112 (2022). https://doi.org/10.1038/s41535-022-00523-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00523-w
This article is cited by
-
Weyl metallic state induced by helical magnetic order
npj Quantum Materials (2024)