Introduction

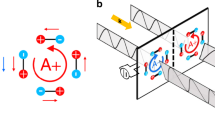
Ferroics are defined as materials possessing some sort of switchable ordering that comes about spontaneously1,2. The ferroaxial order, which is characterized by a rotational structural distortion in a crystal, has been proposed as a new class of ferroic order in recent years3,4,5. Such a rotational distortion is regarded as a vortex of electric dipole moments, an example of which is illustrated in Fig. 1a. The order parameter of the ferroaxial order is the so-called ferroaxial moment \({{{\mathbf{A}}}}\) (or sometimes called electric toroidal moment) defined as \({{{\mathbf{A}}}} \propto \mathop {\sum}\nolimits_i {{{{\mathbf{r}}}}_i \times {{{\mathbf{p}}}}_i}\) where \({{{\mathbf{r}}}}_i\) is a position vector of an electric dipole \({{{\mathbf{p}}}}_i\) at i site from a symmetrical center of the rotation6,7,8. Though \({{{\mathbf{A}}}}\) is symmetric under both time reversal and space inversion, it breaks the mirror symmetry whose mirror plane includes the rotation axis. Thus, ferroaxial order results in the formation of two domain states with the opposite signs of \({{{\mathbf{A}}}}\) (Fig. 1a, b). Note that a mirror symmetry with the mirror plane perpendicular to the rotation axis is not necessarily broken in ferroaxial order, which is distinct from chirality.

Fig. 1: Circular intensity difference (CID) in second harmonic generation (SHG) from ferroaxial materials.
figure 1

a, b Schematic illustrations of a pair of ferroaxial domain states with the opposite sign of ferroaxial moment A defined as \({{{\mathbf{A}}}} \propto \mathop {\sum}\nolimits_i {{{{\mathbf{r}}}}_i \times {{{\mathbf{p}}}}_i}\). Here ri denotes a position vector of electric dipole pi from the symmetrical center of a structural unit. c, d Simplified c-axis views of a pair of ferroaxial domain states (A+ and A− domains) in NiTiO3. e, f Conceptual diagram of CID-SHG from A+ and A− domain states. The red and light green arrows denote fundamental circularly polarized light and SHG, respectively. The size of the light green arrows represents the intensity of SHG. Thus, the intensity of SHG from a ferroaxial material depends on both the circular polarization of fundamental light and the sign of A.

Full size image

Until recently, ways to identify the sign of \({{{\mathbf{A}}}}\) or ferroaxial domain states have not been common as those of chirality with the use of symmetry-dependent physical phenomena, such as optical activity. In these few years, however, domain states of ferroaxial order were experimentally demonstrated by using rotational anisotropy second harmonic generation (SHG)9,10 and electrogyration (EG)11,12. Motivated by the experimental progress, ferroaxial order has attracted growing interest because of its potential for unconventional physical phenomena and new functionalities. For example, it is expected that ferroaxial order causes transverse responses in which input external fields (magnetic field, electric field, and current) induce output conjugate physical quantities (magnetic, electric, and toroidal dipoles, respectively) along the direction perpendicular to both \({{{\mathbf{A}}}}\) and the applied field13,14. As another example, it is theoretically proposed that the application of thermal gradient to ferroaxial insulator induces electric polarization perpendicular to the thermal gradient15.

In this study, we propose an experimental method for three-dimensional imaging of ferroaxial domains, which is based on the circular intensity difference in the optical SHG signal (CID-SHG) from a ferroaxial crystal. SHG is a phenomenon in which coherent light with a frequency twice of a fundamental wave is generated through the second-order nonlinear interaction between light and material16. Due to its sensitivity to symmetry breaking of either spatial or time-reversal operation, it has been widely used to observe the phase transition and visualize the domain structure in ferroics17. Typically, the electric-dipole (ED) contribution is dominant in SHG, and the ED-induced SHG is strictly forbidden in systems with inversion symmetry. Therefore, SHG is usually applied to non-centrosymmetric materials or the surface or interface where the discontinuity breaks the inversion symmetry. Furthermore, SHG using circularly polarized light offers a highly sensitive probe of molecular systems, biomaterials, and surfaces with chiral structures18,19,20. In centrosymmetric systems, however, SHG is allowed if higher-order multipole contributions such as magnetic-dipole (MD) or electric-quadrupole (EQ) contributions are involved. Additionally, the enhancement of SHG has been reported near an optical resonance and is used to observe the domain structure in the case of d-d transition in magnetics17,21. Previous studies on the investigation of ferroaxial order in some ferroaxial materials utilized rotational anisotropy SHG which is ascribed to the EQ contribution9,10.

Here we adopt CID-SHG to identify the sign of ferroaxial moment and to visualize ferroaxial domains in an order-disorder type ferroaxial crystal, NiTiO3, belonging to a centrosymmetric structure with the space group of \(R\bar 3\) (Supplementary Note 1). The idea is inspired by a report on the observation of SHG dependent on circular polarization of fundamental light in the paramagnetic phase of another ilmenite-type compound, MnTiO322. The CID-SHG of MnTiO3 is interpreted in the framework of the MD contribution. We apply this effect to examine ferroaxial order in NiTiO3 and achieve three-dimensional imaging of its ferroaxial domain structures from the surface into the material depth with a sub-micrometer resolution.

Results and discussion

Formulation of circular intensity difference in second harmonic generation

At room temperature, the crystal structure of NiTiO3 is the ilmenite-type with the ferroaxial point group \(\bar 3\) in which Ni and Ti layers are stacked alternately along the hexagonal c axis23. Depending on the ordered sequence (Ni-Ti-Ni-Ti or Ti-Ni-Ti-Ni), two ferroaxial domain states (A+ and A− domains) are formed11, as schematically illustrated in Fig. 1c, d. In the following, we derive CID-SHG of the system with the ferroaxial point group \(\bar 3\). Though this point group is centrosymmetric and forbids the ED-induced SHG, it allows the MD- and EQ-induced SHG. MD and EQ contributions can be represented by the axial tensor of rank 3 and the polar tensor of rank 4, respectively. The equations for SHG in the point group \(\bar 3\) for MD and EQ contributions have been derived in ref. 22. These two contributions provide the same expressions of SHG and calculating both contributions gives us more terms without any quantitative differences (Supplementary Note 2). Therefore, for simplicity, we omit the EQ contribution and take only the MD contribution in the following discussion.

We set the orthogonal axes xyz with z along the light propagation direction. The nonlinear magnetization M induced by MD is described by

$$\begin{array}{*{20}{c}} {M_i^{{{{\mathrm{MD}}}}}\left( {2\omega } \right) \propto \chi _{ijk}^{{{{\mathrm{MD}}}}}E_j\left( \omega \right)E_k\left( \omega \right),} \end{array}$$
(1)

where \(\chi _{ijk}^{{{{\mathrm{MD}}}}}\) is the third-rank nonlinear optical susceptibility tensor and E is an electric field. In the wave equation for the electric field, the MD contribution leads to a source term μ0\(\nabla\)×∂MMD/∂t for SHG. When the light propagation direction (|| z) is parallel to the c axis (hexagonal setting), there are only two independent components to be considered χ(1) = χxxx = −χxyy = −χyxy = −χyyx and χ(2) = χyyy = −χxxy = −χxyx = −χyxx24. The total source term obtained under the present geometry can be described as

$${{{\mathbf{S}}}} \propto \left\{ {\chi ^{\left( 2 \right)}\left( {E_x^2 - E_y^2} \right) + 2\chi ^{\left( 1 \right)}E_xE_y} \right\}{{{\mathbf{e}}}}_x + \left\{ {\chi ^{\left( 1 \right)}\left( {E_x^2 - E_y^2} \right) - 2\chi ^{\left( 2 \right)}E_xE_y} \right\}{{{\mathbf{e}}}}_y,$$
(2)

where ex(y) denotes the unit vector along x(y). When the fundamental light is close to the absorption edge, we need to consider the resonance SHG having the complex susceptibility tensors (\(\chi = \chi ^\prime + i\chi ^{\prime\prime}\)). In this case, the second harmonic (SH) intensity obtained under circularly polarized light can be calculated as follows:

$$I \propto \left( {|\chi ^{\left( 1 \right)}|^2 + |\chi ^{\left( 2 \right)}|^2} \right)\left( {E_ + ^4 + E_ - ^4} \right) + 2\left( {\chi ^{\left( 2 \right)\prime\prime }\chi ^{\left( 1 \right)\prime } - \chi ^{\left( 2 \right)\prime }\chi ^{\left( 1 \right)\prime\prime }} \right)\left( {E_ + ^4 - E_ - ^4} \right),$$
(3)

where E± represents the two components of circular polarization. The second term of Eq. (3) depends on the circular polarization of the fundamental light. This means that the SH intensity obtained by right-handed circularly polarized (RCP) fundamental light differs from that by left-handed circularly polarized (LCP) one in the system with the point group \(\bar 3\).

Furthermore, let us consider the effect of ferroaxial domains on the SH intensity I. A+ and A− domains are converted with each other by the mirror operation with the mirror plane parallel to (110). This mirror operation leads to the sign change of χ(2) but not χ(1) (Supplementary Note 3). Therefore, the sign of the second term of Eq. (3) in the A+ domain is opposite to that of the A− domain. Thus, we can identify the ferroaxial domain state through CID-SHG. Furthermore, spatially resolved measurements such as SHG microscopy using circularly polarized fundamental light allow the visualization of ferroaxial domain structures. The conceptual diagrams of CID-SHG from ferroaxial domains are illustrated in Fig. 1e, f. Under RCP fundamental light, one domain (A+ domain state) exhibits weaker SHG while the other one (A− domain state) exhibits stronger SHG. The situation becomes the opposite when LCP fundamental light is irradiated.

Visualization of ferroaxial domains

We apply the discussion above, namely, CID-SHG between A+ and A− domains, to the visualization of ferroaxial domain structures in NiTiO3. We measured spatial distributions of SH intensity in single crystals of NiTiO3 by SHG microscopy using circularly polarized fundamental light irradiated along the c axis (see “Methods” and ref. 25). For this measurement, we prepared samples with multi-domain states by a proper annealing procedure (see “Methods” and ref. 12). Figure 2c shows the optical transmission microscope image of the (001) face of a sample. In the image, branch-like patterns are seen and correspond to TiO2 impurities. Except for these impurities, the sample is homogeneous, and it is impossible to distinguish ferroaxial domain states in the microscope image. Figure 2a, b shows the two-dimensional SHG images obtained by RCP and LCP fundamental light with a wavelength of 1200 nm, respectively. These images were collected from the same area as that in Fig. 2c. Bright and dark correspond to high- and low-intensity counts, respectively. The magnitude of the normalized CID-SHG in each area, defined as \(|{{\Delta }}I/I_{{{{\mathrm{AVE}}}}}|\) where \({{\Delta }}I = (I_{{{{\mathrm{RCP}}}}} - I_{{{{\mathrm{LCP}}}}})\) and \(I_{{{{\mathrm{AVE}}}}} = \left( {I_{{{{\mathrm{RCP}}}}} + I_{{{{\mathrm{LCP}}}}}} \right)/2\), is 0.6–1.3, meaning that SHG signals from NiTiO3 strongly depend on circular polarization of incident light. In Supplementary Fig. 2, we show \({{\Delta }}I/I_{{{{\mathrm{AVE}}}}}\) as a function of wavelength of fundamental light in an area where \(I_{{{{\mathrm{RCP}}}}}\) is larger than \(I_{{{{\mathrm{LCP}}}}}\). \({{\Delta }}I/I_{{{{\mathrm{AVE}}}}}\) gradually decreases with increasing the wavelength from 1200 to 1380 nm. This wavelength range corresponds to the Ni2+ d–d transition from the 3A2g ground state to the 3T2g state26,27. The color contrast is reversed from the image of Fig. 2a to Fig. 2b except in the impurity regions. Considering the discussion above, the bright and the dark regions correspond to a pair of ferroaxial domains with the opposite sign of ferroaxial moment. The observed domains are irregular in shape with size on a submillimeter scale.

Fig. 2: SHG imaging of ferroaxial domains in NiTiO3 using circularly polarized fundamental light.
figure 2

a, b Two-dimensional maps of SH intensity obtained with (a) right-handed circularly polarized (RCP) and (b) left-handed circularly polarized (LCP) light. Bright and dark regions correspond to either A+ or A− ferroaxial domains. c Transmission optical microscopy image of the area corresponding to the SHG images of (a) and (b). Branch-like patterns in (c) correspond to TiO2 impurities. d Three-dimensional image of SH intensity at the same area as (a) and (b).

Full size image

To further confirm that spatial distributions of the color contrast in Fig. 2a, b reflect ferroaxial domain structures, we compared a CID-SHG image and a ferroaxial domain pattern obtained by an EG measurement11,12 (see also Supplementary Note 4). Supplementary Fig. 3a, b show CID-SHG images of another sample by using RCP and LCP fundamental light, respectively. The contrast reversal is also observed in this sample. Comparing the CID-SHG images (Supplementary Fig. 3a, b) with that obtained by the EG measurement (Supplementary Fig. 3c), their domain patterns well match up with each other. This supports that the area with bright and dark colors in CID-SHG images corresponds to different ferroaxial domain (A+ and A−) states. Thus, we confirm that CID-SHG is effective to visualize ferroaxial domain structures. Compared with other experimental techniques such as measurements of rotational anisotropy SHG and EG, the present CID-SHG measurement has the benefit of a large difference in its signals between A+ and A− domains, \(\left[ {I_{{{{\mathrm{RCP}}}}}({{{\mathrm{A}}}} + ) - I_{{{{\mathrm{RCP}}}}}({{{\mathrm{A}}}} - )} \right]/\left\{ {\left[ {I_{{{{\mathrm{RCP}}}}}({{{\mathrm{A}}}} + ) + I_{{{{\mathrm{RCP}}}}}({{{\mathrm{A}}}} - )} \right]/2} \right\}\) = 32 %. This is large enough to easily distinguish A+ and A− domains. In addition, another merit of CID-SHG is the availability to construct three-dimensional images without any destruction of the specimen. Figure 2d shows a three-dimensional image of SH wave distribution under an RCP fundamental light. The magnitude of SH intensity is nearly constant as a function of sample depth, which means the SH activity remains inside the sample and is not ascribed to the surface effect.

Next, to clarify SHG signals around a domain boundary (DB), we closely looked at the area near the DB. Figure 3a–c display magnified views of two-dimensional SHG images obtained with different polarization of fundamental light in the same area. On the right side of each panel, a cross-sectional profile along a white dashed line is attached. In the images with RCP and LCP fundamental light (Fig. 3a, b), in addition to CID-SHG between A+ and A− domains, a remarkable enhancement of SH intensity at DB is evident. Such an enhancement of SHG at DB is also seen for a measurement using linearly polarized fundamental light, which is displayed in Fig. 3c. The SH intensity is weak in both upper and lower domains, but the SH intensity at DB is around 3–10 times stronger than those from domains. Thus, the enhancement of SHG at DB is observed regardless of the polarization state of fundamental light. We also measured a depth profile of SH intensity using linearly polarized light in the area corresponding to Fig. 3c. Figure 3d shows a three-dimensional image of SH intensity, and its cross sectional cut at the position of the white dashed line is displayed in Fig. 3e. This result shows that the DB is almost perpendicular to the sample surface with keeping almost the same SH intensity. Thus, the enhancement of SH intensity at DB is not the surface effect but the bulk effect.

Fig. 3: Polarization dependence of circular intensity difference in second harmonic generation (SHG) around a ferroaxial domain boundary.
figure 3

a, b Two-dimensional maps of SH intensity obtained with (a) RCP, (b) LCP, and (c) linearly polarized fundamental light. Right panels of (a–c) show the profiles of SH intensity along the white dashed lines of the respective images. In (a), the crystallographic axes are indicated as white arrows. The white arrow embedded in (c) corresponds to the polarization directions of fundamental light and SHG. The upper and the lower areas with different SH intensities by measurements using circularly polarized light correspond to either A+ or A− ferroaxial domains. Regardless of the light polarization, the SH intensity is enhanced at the domain boundary. d Three-dimensional image of SH intensity at the same area as (a–c). e Depth profile in a plane cut at the white dashed line in (d). The bright line represents the depth profile of the domain boundary.

Full size image

Although the materials themselves possess centro-symmetry and are non-polar, the emergence of polar nature at DBs has been observed in various ferroelastic materials such as CaTiO328,29 and LaAlO330. In these materials, flexoelectric effect would play a major role to induce the polarization at DBs. Compared with the results of ferroelastics, the signal to noise ratio of SH intensity from ferroaxial DBs in NiTiO3 is rather weak. It is not surprising since ferroaxial domain itself also produces SH intensity through MD or EQ contribution which is not the case for ferroelastic materials. If ferroaxial DB also possessed finite electric polarization which contributes to the ED-induced SHG, we could observe the drastic intensity difference between domain and DB since the ED contribution is typically much larger than other ones. Therefore, we do not claim that DBs of NiTiO3 is polar. As a possible explanation of the enhancement of SHG at DBs, nonlinear Čerenkov SHG can be considered. Čerenkov SHG normally appears in a planner waveguide, and is recently used to visualize ferroelastic domain boundaries31,32. Furthermore, at some DBs, characteristic fringe-like patterns are observed (see Supplementary Fig. 3d). By comparing the SHG image (Supplementary Fig. 3d) and the EG image (Supplementary Fig. 3c), we find that the fringe-like patterns in the SHG image often appear at green colored areas in the EG image. The green colored areas in the EG image are considered to correspond to thick DBs which are not parallel to the c axis but considerably tilted from the c axis11. Furthermore, a period of the fringe monotonically increases with increasing the wavelength of incident light (not shown). These results suggest that the interference of SHG produced in neighboring ferroaxial domains with tilted angles also contributes to SHG signals at DBs. However, more detailed experiments and analyses will be required to confirm the origin of the enhancement of SHG at DBs.

In summary, we investigated ferroaxial order in an order-disorder type ferroaxial material, NiTiO3, by SHG microscopy using circularly polarized fundamental light. Remarkable CID-SHG with the relative difference of SH intensity more than 60 % was observed between ferroaxial domains with the opposite sign of the ferroaxial moment. The results are well explained qualitatively by considering the transition process of higher-order multipoles such as magnetic-dipole and electric-quadrupole. With the large value of CID-SHG, we succeeded in the three-dimensional visualization of ferroaxial domains. Furthermore, we confirmed that spatial distributions of CID-SHG are nothing other than ferroaxial domains in comparison with the results of EG in the same sample. Compared with other techniques such as rotational anisotropy SHG and EG measurements, the CID-SHG method has the advantage in terms of three-dimensional spatial resolution and electrode-free method, and so on. Thus, the application of CID-SHG beyond the ED approach offers a powerful technique for the investigation of ferroaxial order and three-dimensionally visualizing its domain states.

Methods

Sample preparation

Single crystals of NiTiO3 were grown by the flux method. Details of the growth procedures are described in ref. 12. The obtained crystals were plate-shaped with typical dimensions of 3 × 3 × 0.1 mm3 and were confirmed to be ilmenite-type NiTiO3 by X-ray diffraction measurements. The widest faces of the crystals were perpendicular to the c-axis (hexagonal setting). The as-grown crystals are usually composed of a single ferroaxial domain state. To form multi-domain states, the as-grown crystals were annealed in air from 1623 K at a cooling rate of 1 K h−1. The annealed crystals were polished down to the thickness of 20–60 μm for SHG measurements.

Second harmonic generation microscopy

CID-SHG measurements were performed at room temperature by a scanning transmission microscope. The fundamental light was provided by a femtosecond optical parametric oscillator TOPOL (Avesta) which can produce wavelengths of 680–1000 nm and 1100–2300 nm. In the present study, we mainly used a wavelength of 1200 nm with a repetition frequency of 80 MHz and a pulse width of 125 fs. The power of fundamental light was adjusted by an attenuator, which was composed of a combination of a half-wave plate and a Gran-Taylor prism. The circularly polarized light was produced by a quarter-wave plate and its degree of circular polarization was confirmed to be about 90 %. A pair of objectives with a numerical aperture of 0.65 and a pinhole were used to make a confocal system. The SH intensity was collected by a point detector using a photon counting method. Two-dimensional images of the SH intensity were obtained by scanning an incident wave using a galvanometer scanner. A scanning motor was used to collect two-dimensional images with different depths and constructed three-dimensional images. The spatial resolutions of our system are around 0.56 μm for lateral direction and 3 μm for depth direction.