Introduction

The pseudogap state in high-Tc cuprate superconductors has been a central issue in condensed matter physics1,2,3,4,5,6,7,8,9,10,11. Sr2IrO4 is a pseudospin-1/2 Mott insulator that can be described by the same minimal model as the cuprates, and the appearance of the mysterious pseudogap phase in this non-cuprate system has been the subject of much recent attention12,13,14,15,16,17,18,19,20,21,22,23. Significance of the pseudogap in the electron-doped Sr2IrO4, however, depends on the nature of this gapped state and the extent to which it drives a generic ordering tendency rooted in the shared minimal model, and provides the basis for a wealth of emergent phenomena, including high-Tc superconductivity14,15,16,17,18,19,20,21,22,23,24,25.

Results

Spectroscopic characteristics of the pseudogap state

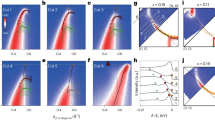
Insight into the character of the pseudogap state can be obtained by scrutinizing the form of gap opening in the electronic band dispersion3,4,5,6,7,8,9,10,11. Accordingly, we have carried out photoemission measurements along the antinodal high-symmetry direction of an electron-doped Sr2IrO4 crystal (Fig. 1, Supplementary Fig. 1), where the pseudogap effect was observed to reach its maximum in the momentum space12,13. The electron doping is realized by potassium surface deposition on a La-doped Sr2IrO4 sample (Supplementary Fig. 2). At high temperature (150 K), when the pseudogap is absent, we see a single band crossing the Fermi level (EF) at two different momentum points (Fig. 1a, d). This is consistent with our tight-binding calculations of the band structure (Fig. 1i and Supplementary Fig. 3) which provide a gapless starting point for investigating the pseudogap state. But, at low temperature (30 K), the dispersion bends back without crossing the Fermi level and gives rise to the pseudogap (Fig. 1e–h). A careful examination of the spectra reveals the following characteristics: (1) the top of the band is not at (π,0) in the gapped state (compare Fig. 1a, b with Fig. 1e, f). (2) The back-bending behavior of the dispersion is clear, but it displays a small curvature (Fig. 1e, f, j), such that the absolute value of the electron velocity in the back-bending region is much smaller than that in the original band. (3) The back-bending momenta in the gapped state [marked by the dark red energy distribution curves (EDCs) in Fig. 1e] are aligned with the Fermi momenta (KF1 and KF2) defined in the gapless normal state (dark red EDCs in Fig. 1a). The preceding points can also be quantitatively visualized by tracing the energy positions of the EDC intensity maxima as a function of momentum at different temperatures. Results are shown in Fig. 1j, where the low-temperature gap minimum (~30 meV) is identified at the high-temperature Fermi momenta (marked by the dashed lines). This energy gap gradually decreases with increasing temperature and disappears between 120 K and 150 K (Fig. 1j and Fig. 2a–c).

Fig. 1: Temperature dependence of the antinodal band dispersion in electron-doped Sr2IrO4.
figure 1

a Raw EDCs of the photoemission spectrum along the antinodal cut divided by the Fermi–Dirac function at 150 K. EDC peak positions are marked by the red circles. The two EDCs at the Fermi momenta are shown in dark red and labeled as KF1 and KF2. b Second derivative image with respect to the energy of the antinodal dispersion at 150 K. c, d The Fermi–Dirac-function-divided (c) and symmetrized (d) EDCs at KF1 and KF2, shown on an expanded scale. e–h, Same as a–d, but measured at 30 K. i Calculated band dispersions along the high-symmetry directions. The color bar represents the relative weight of J = 1/2 to J = 3/2 states. j Dispersion of the intensity maximum as a function of temperature. The energy error bars represent uncertainties in the determination of the EDC peak positions. The momentum error bars are smaller than the size of the symbol. The curvature of the back-bending behavior at low temperature is small, which also gives rise to some uncertainty in the determination of the exact back-bending position. With this error bar, the back-bending momenta measured at several low temperatures are aligned with the Fermi momenta measured at high temperature. The location of the antinodal momentum cut is shown in the inset. Potassium surface deposition was applied to the La-doped sample (Sr1−xLax)2IrO4 (x ~ 0.048) to achieve a high electron doping level (Supplementary Fig. 2), where the appearance of low-temperature quasiparticles enables a quantitative determination of the dispersion in the pseudogap state. An undistorted Brillouin zone is used to make a direct comparison with the cuprates.

Full size image
Fig. 2: Temperature evolution of the EDC at the Fermi momentum.
figure 2

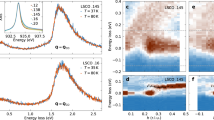
a, b The symmetrized (a) and Fermi–Dirac-function-divided (b) EDC at the Fermi momentum KF1 (defined in Fig. 1), measured at selected temperatures. Fitting results are shown as black lines. The observed quasiparticle peaks at low temperature enable a quantitative determination of the gap. c Gap magnitude as a function of temperature. The gray shading is a guide to the eye. d Extracted FWHM of the EDC peak (red triangles) and the single-particle scattering rate (Γ) from the fits (green rectangles) are presented as a function of temperature. The same quantities for Bi2201 are extracted from ref. 10 and shown here (black circles and blue diamonds) for comparison. Note that the fitting parameter Γ is only used as an independent but empirical estimation of the EDC peak width; this phenomenological model might not be sufficient to describe the experimental spectra and the results of ref. 10. The error bars represent the uncertainty in extracting the FWHM of the EDC peak and in the fitting process.

Full size image

Besides the distinctive band dispersion associated with the pseudogap state, the nature of the pseudogap is also encoded in the spectral line shape10,26. For this purpose, the temperature evolution of the EDC at the Fermi momentum (KF1) is shown in Fig. 2a, b. While the opening of the pseudogap initially depletes the spectral weight at the Fermi level, a sharp quasiparticle peak starts to emerge in the vicinity of the gap at low temperatures (e.g. at 30 K, see Fig. 2a, b). The full-width-at-half-maximum (FWHM) of the peak is extracted and shown in Fig. 2d. It decreases monotonically with decreasing temperature, indicating a reduced scattering rate in the low-temperature regime. The effective single-particle scattering rate (Γ) can also be obtained by fitting the data to a phenomenological model27, which shows a similar temperature evolution as that of the extracted FWHM (Fig. 2d).

Discussion

After establishing the spectroscopic characteristics of the pseudogap state of electron-doped Sr2IrO4 (also see Supplementary Fig. 4), we now compare them with the cuprates and the results of some model calculations to gain insight into their origin. Density-wave orders have been proposed to account for the pseudogap in cupates6,7,8,9,10. With finite scattering wave vectors, these orders would break the particle–hole symmetry and typically compete with superconductivity10,11. Photoemission measurements on Bi2201 (Pb0.55Bi1.5Sr1.6La0.4CuO6+δ) have revealed such particle–hole symmetry breaking as well as spectral broadening with decreasing temperature in its pseudogap phase, supporting the density-wave scenario10. Various density-wave orders have also been reported in electron-doped Sr2IrO418,19,21,22, making them natural candidates for the observed pseudogap. However, for a typical density-wave order, the finite scattering wave vector would push the back-bending momenta away from the Fermi momenta10 (e.g., see Fig. 3b for the simulated photoemission spectrum for a [π,π] density-wave order, also see Supplementary Fig. 5), which is inconsistent with our data (Fig. 3a). One exception is a stripe order with a special wave vector Q that connects the two Fermi momenta in the normal state (Fig. 3c). In this case, although the particle–hole symmetry is broken, the back-bending momenta in the gapped state are roughly the same as the Fermi momenta (Fig. 3c). This scenario seems to be compatible with the momentum-alignment observed in our measurements (Fig. 3a). However, there are key differences as follows. First, the calculated gap near EF (Fig. 3c) is due to hybridization between the main band and the Umklapp bands (main band shifted by ±Q). But such Umklapp bands are absent in our experiments, see Supplementary Fig. 6 for details. This result is repeatable on different ARPES systems with different experimental geometry, photon energy and light polarization. Therefore, the absence of the Umklapp bands is intrinsic and not associated with ARPES matrix element effects. Second, due to the scattering process with the wave vector Q, the slope of the back-bending region near (π,0) should roughly follow that of the main band (Fig. 3c and Supplementary Fig. 7), which is much steeper than the experimental observation (Fig. 3a). Third, besides the gap at EF, the hybridization will also produce several energy gaps below EF (Fig. 3c), which are not seen in our experiments. In addition to the discrepancies in the band dispersion, the temperature evolution of the spectral line width in electron-doped Sr2IrO4 is also different from that observed in the cuprate Bi2201 (ref. 10). As shown in Fig. 2d, the observed sharpening of the quasiparticle peak with decreasing temperature in our experiment is distinct from the competing-order-induced spectral broadening in Bi2201, so that it will be hard to use the same density-wave order to explain the pseudogap state of electron-doped Sr2IrO4.

Fig. 3: Comparison of different electronic orders.
figure 3

a Experimental dispersion in the normal and gapped states. b–d, Simulated spectra for commensurate [π, π] density-wave order (b), stripe order with a wave vector connecting KF1 and KF2 (c) and superconducting order (d). Red curves represent the bare band in the simulation. Black dashed lines mark the back-bending momenta in the gapped states.

Full size image

Since the experimental observations cannot be explained by the simple density-wave scenarios with a finite Q, we next consider an electronic order with zero scattering wave vector (Q = 0). The existence of such an order requires an order parameter not commuting with the Hamiltonian when all sites are summed over. Therefore, neither charge nor spin can form an order with Q = 0 in the single-band model. An excitonic order with Q = 0 may exist, but it requires the particle and hole to reside in two different bands, which is not the case in Sr2IrO4. The textbook example of an order with Q = 0 is the BCS superconductivity in which the Bogoliubov quasiparticle exhibits particle–hole symmetry. As shown in Fig. 3d, the back-bending momenta in the superconducting state are perfectly aligned with the Fermi momenta in the normal state. The slope of the back-bending region near (π,0) is very gentle, mimicking that in the experiment. However, the superconducting scenario also has problems. First, no transport evidence for superconductivity has ever been reported in doped Sr2IrO4, although spectroscopic indications have been reported on surface-doped samples, possibly due to a higher doping level than the bulk doping limit16,17,21. Second, the gap-closing temperature in our experiment is between 120 and 150 K, which is comparable to the highest Tc in the cuprates. However, possible superconductivity in electron-doped Sr2IrO4, if any, is predicted to appear at a much lower temperature than that in the cuprates due to a smaller on-site Coulomb repulsion14,15. Third, although the energy gap starts to appear at 120 K, the quasiparticle peak remains very weak until a much lower temperature is reached (Fig. 2). This is distinct from the superconducting state, where the apparent Bogoliubov quasiparticles should appear with the superconducting gap.

A model considering the Q = 0 order with a limited correlation length might better capture the experimental results. In the example of superconductivity, this would refer to the picture of preformed Cooper pairs. In Fig. 4, we show the simulated spectra for preformed Cooper pairs as a function of the correlation length, see Supplementary Methods for details. While the subtle back-bending behavior and its momentum alignment with KF are satisfied for all correlation lengths (Fig. 4a), a smaller magnitude of the gap and a weaker quasiparticle peak are clearly associated with a shorter correlation length (Fig. 4b). The fully gapped spectrum with a sharp quasiparticle peak appears when the correlation length becomes much longer. If we assume that the correlation length in the real material becomes longer at lower temperatures, then the above simulation would also be qualitatively consistent with the temperature evolution of the spectra observed in our experiment (Fig. 2). We note that the simple simulation might not fully capture the complexity of the strongly correlated system, but the overall agreement suggests the preformed Cooper pairs as a viable mechanism for the observed pseudogap state of electron-doped Sr2IrO4.

Fig. 4: Simulation of preformed Cooper pairs as a function of the correlation length.
figure 4

a Simulated spectra with selected correlation lengths (ξ = 8000, 3500, 2500, 1500 and 500 lattice parameter). The dashed black curves represent the bare band in the simulations. b EDC at the Fermi momentum, as a function of correlation length. c Gap magnitude as a function of correlation length, extracted from the simulated EDC at the Fermi momentum. Note that the absolute value of the correlation length in the simplified model cannot be directly compared with that in the real material, see Supplementary Methods for details.

Full size image

However, a key question of whether the electron-doped Sr2IrO4 becomes superconducting at low temperature remains unresolved. Since the highest bulk electron doping level in Sr2IrO4 is still limited, potassium surface doping has been used to significantly enhance the electron doping level. However, transport measurements on potassium surface-doped samples remain a technical challenge. An earlier study reported a d-wave gap on potassium surface-doped Sr2IrO4 samples16, where the gap near the node closes at ~30 K. In our measurements, the pseudogap in the antinodal region closes between 120 and 150 K. These results seem to be analogous to those in the underdoped cuprates28. In this sense, it would also be interesting to explore whether other special electronic orders may play a role. Notably, an incommensurate spin density wave with a relatively high transition temperature has been reported in electron-doped Sr2IrO4 samples18. It has been reported that an incommensurate charge density wave order in transition-metal dichalcogenides induces little change on the band dispersion but significantly contributes to the pseudogap29,30. In this sense, some incommensurate density wave orders are very difficult to identify by ARPES. Whether such a phenomenon would take place in electron-doped Sr2IrO4 remains to be understood. Also, preformed Cooper pairs and competing orders may coexist in the cuprates, but dominate in different regions of the phase diagram31. The extent to which similar phenomena may be at play in the iridates remains to be explored.

Finally, we comment on the gapless normal state of electron-doped Sr2IrO4. While the band dispersion shows clear Fermi crossings at high temperature (Fig. 1a, c), the quasiparticle peak near EF is very weak (Fig. 1a, c; Supplementary Fig. 8). Notably, a similar phenomenon has been observed in iron-based superconductors, where the energy gap closes at high temperature but no quasiparticle peak is present in the normal state32. A transition from the coherent quasiparticle to an incoherent strange metal has also been reported in the normal state of cuprates31. While the mechanism is still under debate, the disappearance of a well-defined quasiparticle points to a non-Fermi liquid behavior of the normal state.

Our study shows that the pseudogap state of the electron-doped Sr2IrO4 is consistent with the appearance of a short-range order with zero scattering wave vector. For such an order, the particle–hole symmetric preformed Cooper pairs represent a viable mechanism that has been identified over a wide doping range in the cuprates3,4,5,11,31. If these incoherent Cooper pairs underlie the pseudogap state of electron-doped Sr2IrO4 then superconductivity will likely be driven by the appearance of phase coherence in the system. It will also be interesting to explore whether other unknown orders could be at play with the experimentally identified properties. Further investigation of such an order and its relationship with the incoherent gapless normal state and superconductivity will help unravel the generic physics of doped spin-1/2 Heisenberg antiferromagnetic Mott insulators beyond the material-specific properties of the cuprates.

Methods

Sample growth

Single crystals of (Sr1−xLax)2IrO4 were grown via a platinum (Pt) crucible-based flux growth method as described in earlier studies18. The electron doping was realized by in situ surface potassium deposition on the La-doped sample (Sr1−xLax)2IrO4 with x~0.048.

ARPES measurement

The bulk La-doped sample was used as the starting point for the surface doping in order to avoid the possible charging effect of the bulk material during ARPES measurements. The sample was cleaved in situ at 150 K, with a base pressure of better than 3 × 10−11 Torr. ARPES measurements were carried out at Beamline 5-4 of the Stanford Synchrotron Radiation Lightsource (SSRL) of SLAC National Accelerator Laboratory using 25 eV photons with a total energy resolution of ∼9 meV. The Fermi level was referenced to that of polycrystalline Au in electrical contact with the sample. Details of theoretical calculations are described in the Supplementary Methods.