Introduction

Frustrated magnets provide an ideal playground for exotic emergent phenomena1,2. In many cases, gauge structures can emerge due to local constraints imposed by competing interactions, giving rise to exotic states of matter like quantum spin liquid with fractionalised excitations and long-range entanglement3,4,5,6,7,8,9. Excitations violating such local constraints are frequently referred to as spinons, which are the gauge charges in the emergent gauge theory10,11,12. Spinons are point-like topological defects since a single spinon cannot be created/annihilated locally and such processes must be involved in pairs. Meanwhile, gauge theories also support string-like excitations, which connect a pair of spinons with opposite charges and mediate the effective interaction between them. While the spinon pair is annihilated along a non-contractible closed trajectory, such string becomes topological in nature, which we dub as ‘topological string’13,14.

In contrast to spinon excitations that are typically located at higher energies, quantum strings are basic degrees of freedom participating in low-energy physics. Their dynamics reflects the fluctuations of the background gauge field15,16. Quantum strings are 1d objects in space that can be described as two-dimensional worldsheets in spacetime17. As emergent topological defects with finite dimensions, strings have much more internal degrees of freedom (corresponding to their vibration) and are thus expected to bring much richer physics. Strings appear in broad contexts in condensed matter physics, such as in high-temperature superconductors18,19,20,21,22, quantum spin ice23,24,25 and incommensurability18,26,27. They can even be directly observed via the ultra-cold atoms in the optical lattice28,29. However, in contrast to well-studied point-like excitations, strings are paid much less attention.

The quest for exploring string dynamics is also motivated by the rapid progress on frustrated rare-earth materials. Recently, a number of rare-earth pyroclore, Kagomé and triangular lattice magnets have been evidenced to be described by frustrated quantum Ising models30,31,32,33,34,35 which exhibit emergent gauge structures. For the triangular lattice, a large class of materials are described by the transverse field Ising model (TFIM)31,34, a typical model that can be understood from the perspective of topological strings15,16,29: String picture can be utilised to understand its phase diagram15,16 as well as to depict the quantum fluctuations therein36,37,38,39. Among these materials, a typical one is TmMgGaO4 (TMGO). The spin excitation spectra was recently discovered in the neutron scattering experiment31, and the so-called ‘roton’ excitation was claimed to relate to the BKT physics33,40,41. However, direct signatures of string excitations are absent from the neutron spectrum.

In this manuscript, we study a generic antiferromagnetic TFIM on the triangular lattice relevant to triangular lattice rare-earth compounds. Through large-scale quantum Monte Carlo (QMC) simulations42, we focus on the dynamical signatures of quantum string excitations. At weak transverse field, we find continuum excitations at low energies that accords with the internal vibration and mutual interactions of quantum strings. In particular, the internal vibration matches well with the continuous spectrum of spin-1/2 XY chain, while the string interactions induce excitations exhibiting features of Luttinger liquid43. It should be noted that these continuum spectroscopic properties go beyond the effective field theory, where for the latter only coherent spin waves were predicted at low energies. Our work provides insight into understanding the dynamical properties of triangular quantum Ising antiferromagnet such as TMGO.

Results

Starting from rare-earth compounds

We begin with the nearest-neighbour spin-1/2 TFIM relevant to triangular rare-earth compounds

$$H = J\mathop {\sum}\limits_{\langle ij\rangle } {S_i^zS_j^z} - \Delta \mathop {\sum}\limits_i {S_i^x}$$
(1)

Here S is the effective spin-1/2 moment acting on the lowest two crystal field levels of the non-Kramers ion. J denotes the nearest neighbour antiferromagnet coupling and the Δ is the energy splitting between the lowest crystal-field levels. The origin of the crystal field splitting term Δ depends on the nature of crystal field levels. For non-Kramers doublet systems, the crystal field degeneracy is protected by the C3 on-site point group symmetry, therefore Δ is induced by breaking such symmetry, e.g., by applying in-plane uniaxial pressure. For TMGO and some other Tm-based materials, the lowest two crystal field levels form a nondegenerate dipole-multipole doublet. The lowest crystal fields exhibit intrinsic splitting Δ since they carry the singlet representation of the point group. To quantitatively compare with the TMGO experiment, we also introduce a next-nearest-neighbour interaction \(H_{{\it{J}}^\prime } = {\it{J}}^\prime \mathop {\sum}\nolimits_{\langle \langle ij\rangle \rangle } {S_i^zS_j^z}\) perturbation term to the Hamiltonian34. The effective model is illustrated in Fig. 2c inset.

The best-fit parameters for TMGO were found in the former work33 to be J = 0.99 meV, j′ = 0.05 meV and Δ = 0.54 meV. Hereafter we set the NN coupling as the energy unit J = 1. We carry out a QMC simulation42,44,45 combined with SAC technique46,47,48 to measure the spin excitation spectrum. The simulation is performed on L × L lattice (L = 24) with periodic boundary conditions. The temperature is set T = 1/4L = 1/96 to mimic the ground state result. In inelastic neutron scattering experiments, what is measured is the dynamical Sz -Sz correlator given by

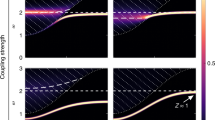
$${{{\mathcal{S}}}}^{zz}({{{\mathbf{q}}}},\omega ) = \frac{1}{{2\pi L^2}}\mathop {\sum}\limits_{ij} {{\int}_{ - \infty }^{ + \infty } {dt\,e^{i{{{\mathbf{q}}}} \cdot ({{{\mathbf{r}}}}_i - {{{\mathbf{r}}}}_j) - i\omega t}\langle {S_i^z(0)S_j^z(t)} \rangle } }$$
(2)

Our measured excitation spectrum is presented in Fig. 1a.

Fig. 1: The spectra at different transverse field Δ.
figure 1

a The parameter Δ = 0.54 and J′ = 0.05 corresponds to the material TMGO. b Δ = 0.35, J′ = 0.35 and (c) Δ = 0.20, J′ = 0.020 are for lower energy splitting. The circled areas in (c) demonstrate the splitting of two branches. The path taken in the Brillouin zone is specified in the inset of (a). The spectra are plotted in logarithmic scale to accommodate more details. For the plots in linear scale, see Supplementary Fig. 2.

Full size image

At the parameters for TMGO, the simulated result agrees well with the previous inelastic neutron scattering experiment31 and the previous QMC work33 (See Supplementary Fig. 1). Notice that for TMGO, Δ is large where the system has been close to the clock-paramagnetic transition point (Fig. 2f). To gain a better understanding of the physics deep in the clock phase, we also measure the excitation spectra with decreased Δ. We find that with decreasing Δ, the spectrum splits into two branches. The higher-lying and lower-lying branches lie at the energy scale of J and Δ, respectively, see Fig. 1b, c.

Fig. 2: An illustration of the emergent strings in frustrated TFIM.
figure 2

a An example of string mapping of a spin configuration. Strings 1, 2 and 3 don’t involve triangle-rule-breaking configurations and are thus directional. The l and r vectors on string 1 denote the two directions of the segments. The spin chain labelled τ on the left illustrates the effective spin-1/2 configuration mapped from string 1. The orange and cyan shaded angles on string 1 denote a kink-antikink pair. The pink shaded area illustrates that two nearby strings induce repulsion. String 4 is a closed non-topological string connecting two spinons denoted by red and blue points. b The elementary flipping process brought by the transverse field \(|{{{\mathbf{lr}}}}\rangle \leftrightarrow |{{{\mathbf{rl}}}}\rangle\). The transverse field acts upon the shaded spin. c The ground state string density as a function of anisotropy λ and NNN coupling J′, obtained from large scale QMC simulation. Inset: an illustration of the lattice setup. d, e Configuration and string correspondence of two specific phases: stripe phase (d) with average string density \(\langle \rho _{{{\mathrm{s}}}}\rangle = 0\) and clock phase (e) with \(\langle \rho _{{{\mathrm{s}}}}\rangle = 2/3\). The collapsed arrows denote the superposition of spin-up and down. Correspondingly, the strings are superpositions of configurations denoted by the solid and dashed lines. f The phase diagram at λ = 1 and J′ = 0, at different transverse field Δ.

Full size image

The string description

To better understand the two branches of excitations, we first consider the classical Ising limit Δ = 0. In this case, the ground state is macroscopically degenerate, consisting all the configurations that satisfy the ‘2-up-1-down’ or ‘1-up-2-down’ triangle-rule within each elementary triangle. Such local constraints give rise to emergent U(1) gauge structures at low energies which further lead to emergent topological strings and topological sectors. Instead of understanding strings from dimers and gauge theories, here we present a more intuitive way from an alternative domain wall perspective49,50,51. We choose the stripe state (Fig. 2d) as the reference configuration. The reason we choose the stripe state as the reference state is that any local operation acting upon this state violates the local constraint, hence there are no low-energy excitations within the stripe bulk. With this setup, all spin configurations which obey the triangle-rule can be expressed as domains of stripe state, where domain walls form closed directed strings (Fig. 2a, strings 1–3). In other words, one selects out the bonds in x-direction connecting anti-parallel spins, and connects their mid-points into strings. The strings can be visualised in measurements (See Supplementary Fig. 4). Under periodic boundary conditions, strings wrapping around non-contractible loops cannot be created or annihilated within finite steps of operation, which strongly reflects its topological feature in nature. Therefore the number of topological strings Ns can be used to label different topological sectors. On the other hand, breaking of triangle-rule corresponds to spinon excitations at the energy scale of J15,16 (Fig. 2a, string 4). This is related to the high energy excitations.

Once the transverse field Δ is turned on, quantum dynamics are present. When Δ ≪ J, the low energy excitations do not mix up with the spinon excitations at a higher energy level. As shown above, the low energy quantum excitations are completely provided by the quantum strings. Here we first consider the excitations where only one string is involved, i.e., the internal vibration of a single string. The shape of a string is specified by its segments \(\{ {{{\mathbf{s}}}}_1, \ldots ,{{{\mathbf{s}}}}_{L_y}\}\), which take on the values r and l (shown in Fig. 2a). Upon the action of the transverse field, a pair of antiparallel nearest-neighbour spins are flipped, i.e., \(\left| { \ldots {{{\mathbf{rl}}}} \ldots } \right\rangle \leftrightarrow \left| { \ldots {{{\mathbf{lr}}}} \ldots } \right\rangle\) (Fig. 2b). According to the first-order perturbation theory, these fluctuations can be mapped onto a spin-1/2 XY chain, with spin values τz = ±1/2 represents r and l segments

$$H_{{{{\mathrm{eff}}}}} = - \frac{{\Delta }}{2}\mathop {\sum }\limits_{i = 1}^{L_y} \left( {\tau _i^ + \tau _{i + 1}^ - + \tau _i^ - \tau _{i + 1}^ + } \right)$$
(3)

The effective model is exactly solvable under Jordan-Wigner transformation. Therefore, one can predict a continuous spectrum due to effective Jordan-Wigner fermions excitations corresponding to kink-antikink pairs in the language of strings. This vibration also brings an energy favour Ek = −ΔLy/π to each string, stablizing it energetically against perturbations.

When multiple strings are considered, their interaction becomes significant to the quantum excitations. The non-crossing condition first imposes a hard-core repulsion on strings. The vibration of strings then turns this hard-core repulsion into a dynamic one49. Specifically, when two strings come close to each other (e.g., the string 2 and 3 in Fig. 2a), their vibration will be constrained, reducing the energy gain from internal vibration (See Supplementary Note 1). This loss of vibration energy can be equivalently regarded as the repulsion interaction between them. As former work27 has identified, the dynamic repulsion can be described by a power-law long-range potential. In other words, the internal vibration of strings can also generate mutual dynamic interaction among them.

Dilute string limit

The vibration inside the strings, together with the repulsion interaction between them, determines the low energy excitations of TFIM. To study these two kinds of excitations separately, we turn to the dilute string limit where the strings are far apart and the interaction between them is weak, so that the internal string vibration is not affected by string interaction. This can be parametrised by a quantity called the string density ρs = Ns/Lx. The string density is determined by measuring the nearest-neighbor correlation \(\left\langle {\rho _{{{\mathrm{s}}}}} \right\rangle = \frac{1}{2}\left( {1 - 4\left\langle {S_{{{\mathbf{r}}}}^zS_{{{{\mathbf{r}}}} + {{{\hat{\mathbf x}}}}}^z} \right\rangle } \right)\). In particular, the stripe phase and clock phase, whose configurations and string correspondence are depicted in Fig. 2d, e, have averaged string density \(\left\langle {\rho _{{{\mathrm{s}}}}} \right\rangle _{{{{\mathrm{stripe}}}}} = 0\) and \(\left\langle {\rho _{{{\mathrm{s}}}}} \right\rangle _{{{{\mathrm{clock}}}}} = 2/3\). The string density can be tuned through introducing various perturbations, like the nearest-neighbour exchange anisotropy \(H_\lambda = (\lambda - 1)J\mathop {\sum}\nolimits_{\langle ij\rangle _x} {S_i^zS_j^z}\)27. Here \(\left\langle {ij} \right\rangle _x\) denote the NN bonds in x-direction (Fig. 2c inset). The string density ρs(λ, J′) as a function of exchange anisotropy λ and NNN interaction J′ are measured through a Monte Carlo simulation, shown in Fig. 2c (See Supplementary Note 2). By increasing J′, the system enters the stripe phase from the clock phase through a first-order transition; by decreasing λ, the string density ρs decreases from 2/3 to 0 continuously.

We take J′ = 0 and tune 0 < λ < 1 to fine-tune the string density to a comparatively low lever \(\left\langle {\rho _{{{\mathrm{s}}}}} \right\rangle = 1/3\) and 1/2. The energy hierarchy in the spectrum persists (Fig. 3a). The spinon branch and the string branch stay at the energy scale of J and Δ, respectively. To look more carefully into the string excitations, we scrutinise the low energy spectrum along ΓM and ΓKM lines (Fig. 3b–e).

Fig. 3: The spectra at low string density.
figure 3

a The spectra at string density ρs = 1/3 measured at λ = 0.895, Δ = 0.2, system size L = 24 and temperature T = 1/96 in the unit of J. The path taken in the Brillouin zone is specified in the inset. b, c The zoom-in of low energy region are dived into parallel to the strings (b) along ΓM line and perpendicular to the strings (c) along ΓKM line respectively. d, e The low energy excitation spectra measured at λ = 0.91 and ρs = 1/2 includes parallel to the strings (d) along ΓM line and perpendicular to the strings (e) along ΓKM line respectively. The dashed lines denote the anticipated results in spin-1/2 XY chain (b, d) and Luttinger liquid (c, e). The gray italic momentum labels ‘0’ and ‘2kF’ are the momenta measured from the Fermi point of the projected 1d system.

Full size image

The spectrum along the ΓM line corresponds to the internal string vibration. In the case of nearly independent strings at ρs = 1/3 (Fig. 3b), the spectrum is continuous and enveloped by two dome-like curves, most extensive at Γ point and shrinking when moving towards M point. We find these features in good agreement quantitatively with the continuous spectrum of spin-1/2 XY chain (Fig. 3b, grey dashed lines) (See Supplementary Note 5), where Γ and M points correspond to k = π and 0 momenta of the effective XY chain, respectively. On the other hand, when increasing the string density, the effective repulsion affects the internal vibration of strings, rendering the excitation gapped (Fig. 3d).

The spectrum along the ΓKM line corresponds to the dynamics that come from string interaction. The spectrum exhibits continuous features. Two nearly gapless points locate at \(k_x = \pi (2 - \langle \rho _{{{\mathrm{s}}}}\rangle )\) and \(\pi (2 - 3\langle \rho _{{{\mathrm{s}}}}\rangle )\) (Fig. 3c, e). Whether these points are truly gapless depends on the commensuracy of the string density. At commensurate string density (such as \(\langle \rho _{{{\mathrm{s}}}}\rangle = 2/3\) in clock phase), the high order scattering process will open a gap in the excitation. However, such gap lies at a much lower energy level than our string description. The dispersions in the vicinity of the nearly gapless points are linear. These features hint at the spectroscopic similarity to Luttinger liquid43 (See Supplementary Note 3). In fact, projecting onto the perpendicular direction, the strings can be described with spinless fermions with long-range repulsion moving in 1 d. The two nearly gapless points correspond to the momentum points 0 and 2kF measured from the Fermi point, with the Fermi momentum of the strings \(k_{{{\mathrm{F}}}} = \pi \langle \rho _{{{\mathrm{s}}}}\rangle\), in accordance with the spectroscopic features of ‘Luttinger string liquid’ (Fig. 3c, e, dashed lines).

String and spinon spectra

Having figured out the relation between different string-related excitations and their features in the spectrum, we now return to the isotropic case (i.e., the exchange anisotropy is tuned to λ = 1). To locate the excitations of different topological defects in the spectrum, we try to isolate the contributions from string and spinon excitations. We define a kink operator, which singles out the flippable spins at the kinks of the strings (See Supplementary Note 4), and a spinon operator, which singles out the spins on triangles with the same spin polarization. As the kink operator is only sensitive to string excitations, and the spinon operator only to spinon excitations, their dynamic correlations isolate the contribution of two respective excitations – At low field Δ = 0.2 (Fig. 4a, d), the string spectrum has only low energy part and the spinon spectrum have only high energy part; while for higher Δ (Fig. 4c, f), the energy scales of two excitations nearly coincide, and they mix up into what we see in the spin spectrum measured by neutron scattering.

Fig. 4: The separated spectra of string excitations and spinon excitations.
figure 4

String spectra (a–c) and spinon spectra (d–f) with L = 24 and T = 1/96 at Δ = 0.20, J′ = 0.020 (a, d), Δ = 0.35, J′ = 0.035 (b, e) and Δ = 0.050, J′ = 0.050 (c, f).

Full size image

Discussion

Our work focuses on the dynamical signature of quantum string excitations. We simulate the spectrum of frustrated TFIM on the triangular lattice, which is relevant to a large class of rare-earth magnets including the recently discovered TMGO. At low transverse field, we find continuum excitations at low energies. We show that the features of this continuum are in good agreement with the internal vibration and mutual interactions of quantum strings. In particular, the internal vibration (spectrum along ΓM line) matches well with the continuous spectrum of spin-1/2 XY chain, and the string interaction (spectrum along ΓKM line) induces excitations which exhibit the features of Luttinger liquid. Several trials can be considered in the experiment to observe the string-related excitations in the excitation spectra. If we can find materials with appropriate Δ/J, we expect well separation of string-related excitations from spinons in excitation spectrum31,33,52,53. In experiments, we can also study anisotropic models by applying in-plane uniaxial pressure. On the one hand, for non-Kramers doublet systems, the crystal field splitting Δ is generated and can be tuned by the applied pressure. This enables discovering string related excitations with appropriate Δ. On the other hand, the applied pressure also produces exchange anisotropy λ, which tunes the string density ρs. With sufficiently large λ one would access the dilute string region where the intra-string excitations may be observed. Besides rare-earth magnets, similar phenomena are also expected in other systems such as antiferroelectric materials54, cold atoms55 and quantum computer 56.

Our work not only provides insight into understanding the dynamical properties of triangular quantum Ising antiferromagnet such as TMGO, but also provides iconic features in the spectrum for the experimental search for emergent strings, as well as deepening the understanding of emergent quantum strings in general.

Methods

Stochastic series expansion (SSE)

We use SSE algorithm for the quantum Monte Carlo simulation of the transverse field Ising model42,44,45. In SSE, the evaluation of partition function Z is done by a Taylor expansion, and the trace is taken by summing over a complete set of suitably chosen basis.

$$Z = \mathop {\sum}\limits_\alpha {\mathop {\sum}\limits_{n = 0}^\infty {\frac{{\beta ^n}}{{n!}}\left\langle \alpha |\left( { - H} \right)^n|\alpha \right\rangle } }$$
(4)

By writing the Hamiltonian as the sum of a set of operators whose matrix elements are easy to calculate \(H = - \mathop {\sum}\nolimits_i {H_i}\) and truncating the Taylor expansion at a sufficiently large cutoff M, we can further obtain

$$Z = \mathop {\sum}\limits_\alpha {\mathop {\sum}\limits_{\{ i_p\} } {\beta ^n\frac{{(M - n)!}}{{M!}}\left\langle \alpha \left|\mathop {\prod }\limits_{p = 1}^n H_{i_p}\right| \alpha \right\rangle } }$$
(5)

To carry out the summation, a Markov chain Monte Carlo procedure can be used to sample the operator sequence {ip} and the trial state α. Diagonal update, where diagonal operators are inserted into and removed from the operator sequence, and cluster update, where diagonal and off-diagonal operates convert into each other, are adopted in the update strategy. For more details, see Supplementary Method 1.

Stochastic analytical continuation (SAC)

We adopted the SAC method to obtain the spectral function S(ω) from the imaginary time correlation G(τ) measured from QMC46,47,48. The spectral function S(ω) is connected to the imaginary time Green’s function G(τ) through an integral \(G(\tau ) = {\int}_{ - \infty }^\infty {{{{\mathrm{d}}}}\omega S(\omega )K(\tau ,\omega )}\) where K(τ,ω) is the kernal function. For spin systems, \(K(\tau ,\omega ) = (e^{ - \tau \omega } + e^{ - (\beta - \tau )\omega })/\pi\). To ensure the normalization of spectral function, we further modify the transformation,

$$G(\tau ) = \mathop {\int}\limits_0^\infty {\frac{{{{{\mathrm{d}}}}\omega }}{\pi }} \frac{{e^{ - \tau \omega } + e^{ - (\beta - \tau )\omega }}}{{1 + e^{ - \beta \omega }}}B(\omega )$$
(6)

where \(B(\omega ) = S(\omega )(1 + e^{ - \beta \omega })\) is the renormalised spectral function.

In practice, G(τ) for a set of imaginary time \(\tau _i(i = 1,\, \ldots N_\tau )\) is measured in QMC simulation together with the statistical errors. The renormalised spectral function is parametrised into large number of δ-functions \(B({\it{\omega }}) = \mathop {\sum}\nolimits_{i = 0}^{N_{\it{\omega }}} {a_i\delta ({\it{\omega }} - {\it{\omega }}_i)}\) whose positions are sampled. Then the fitted Green’s functions \(\tilde G_i\) from Eq. (6) and the measured Greens functions \(\bar G_i\) are compared by the fitting goodness \(\chi ^2 = \mathop {\sum}\nolimits_{i,j = 1}^{N_\tau } {\left( {\tilde G_i - \bar G_i} \right)\left( {C^{ - 1}} \right)_{ij}\left( {\tilde G_j - \bar G_j} \right)}\) where Cij is the covariance matrix. A Metropolis process is utilised to update the series in sampling. The weight for a given spectrum is taken to follow a Boltzmann distribution \(W(\{ a_i,\omega _i\} )\sim {{{\mathrm{exp}}}}\left( { - \chi ^2/2{{\Theta }}} \right)\) with \({{\Theta }}\) a virtue temperature. All the sampled spectral functions are then averaged to obtain the final result. For more details, see the Supplementary Method 2. As an evidence of the validity of SAC, we also compare the spectral function obtained from SAC with the lowest excitation frequency extracted directly from the imaginary time correlations (see the Supplementary Fig. 3).