Abstract
High pressure is an effective tool to induce exotic quantum phenomena in magnetic topological insulators by controlling the interplay of magnetic order and topological state. This work presents a comprehensive high-pressure study of the crystal structure and magnetic ground state up to 62 GPa in an intrinsic topological magnet EuSn2P2. With a combination of high resolution X-ray diffraction, 151Eu synchrotron Mössbauer spectroscopy, X-ray absorption spectroscopy, molecular orbital calculations, and electronic band structure calculations, it has been revealed that pressure drives EuSn2P2 from a rhombohedral crystal to an amorphous phase at 36 GPa accompanied by a fourfold enhancement of magnetic ordering temperature. In the pressure-induced amorphous phase, Eu ions take an intermediate valence state. The drastic enhancement of magnetic ordering temperature from 30 K at ambient pressure to 130 K at 41.2 GPa resulting from Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions likely attributes to the stronger Eu–Sn interaction at high pressure. These rich results demonstrate that EuSn2P2 is an ideal platform to study the correlation of the enhanced RKKY interactions, disordered lattice, intermediate valence, and topological state.
Similar content being viewed by others
Introduction
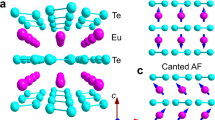
Topological materials have recently emerged as a frontier of condensed matter physics and materials research due to their rich quantum phases and potential applications in future dissipationless topological electronics and quantum computations (for reviews see refs. 1,2). Among them, intrinsic magnetic topological systems are particularly interesting due to the potential applications in spintronic devices. Compared to dilute magnetic topological insulators, intrinsic magnetic materials are stoichiometric magnetic compounds that provide an easily synthesized, tunable, and clean platform to study magnetic topological materials with new intriguing quantum states. Such intrinsic magnetic topological materials are generally narrow-gap semiconductors that combine nontrivial band topology and intrinsic magnetic order3. The intriguing interplay between magnetic ordering and topological states can generate exotic topological quantum phenomena, such as the quantum Hall effect4,5,6, axion electrodynamics7,8,9,10, and Majorana states11. Efforts in the study of emergent phenomena in intrinsic magnetic topological systems are mostly focused on MnBi2Te46,9,12,13,14 due to the very few available candidate materials. Very recently, a series of Eu-based compounds have been demonstrated experimentally, or proposed theoretically, to be intrinsic topological semimetals5,15,16,17,18. Among them, EuSn2P2 has been shown to be a magnetic topological system with type-A antiferromagnetic (AFM) order below 30 K15. EuSn2P2 crystallizes in a layered rhombohedral structure with space group of \({\mathrm{R}}\bar{3}m\), similar to the A2B3 family of topological insulators19. It is comprised of strongly magnetic Eu layers sandwiched between Sn-P layers. Traditionally, Eu-based intermetallic materials have achieved considerable interest for their rich properties including magnetic phases from the strong local moment, valence transition, superconductivity, heavy-Fermion states, and Kondo physics20. Despite of the rich quantum phenomena, much work is needed to understand the intriguing properties. In this work pressure is employed to control the crystal structure, magnetic, and valence states. Pressure has been proven to be a clean and effective way to tune the atomic distances and therefore electronic interactions to induce interesting quantum phenomena in materials, such as superconductivity, magnetism, or electronic topological transitions. For example, pressure-induced suppression of Néel temperature and the emergence of superconductivity have been observed in magnetic compounds including heavy Fermions and iron-based superconductors21,22.
Here we report the systematic high-pressure investigation in EuSn2P2 using a combined experimental approach including angular-dispersive X-ray diffraction (XRD), time-domain synchrotron Mössbauer spectroscopy (SMS), partial fluorescence-yield X-ray absorption spectroscopy (PFY-XAS), and molecular orbital and electronic band structure calculations. In EuSn2P2 the rhombohedral crystal structure remains stable up to 33 GPa before transforming to an amorphous phase. Surprisingly, an impressive over fourfold enhancement in magnetic ordering temperature (To) from 30 K at ambient pressure to 130 K at 41.2 GPa has been observed, despite of an increased mean valence above 20 GPa. The enhancement of magnetic exchange interaction is likely attributed to the stronger Eu–Sn interaction under pressure. This comprehensive study presents intriguing interplay of crystal structure, magnetic ground state, and the associated valence state tuned by high pressure.
Results
Pressure-induced crystalline to amorphous transition
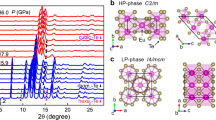
The evolution of structural properties of EuSn2P2 under hydrostatic pressure has been investigated by high resolution XRD experiments. The XRD data reveal that the ambient rhombohedral structure is maintained under pressure up to 33 GPa. At higher pressure the sample loses the long range crystalline order and becomes amorphous at 36 GPa, evidenced by the loss of sharp crystalline diffraction peaks (see Fig. 1). With further compression the amorphous phase persists up to 62 GPa, the highest pressure measured in this study. The observed pressure-induced amorphization (PIA) contrasts with the rhombohedral-to-monoclinic transition reported in EuSn2As223. The lattice parameters, interatomic distances, and unit cell volume of EuSn2P2 in the crystalline phase obtained from the Rietveld refinements from both XRD runs are plotted as a function of pressure (Fig. 2). Parameters from run 1 with helium as hydrostatic pressure medium and run 2 with neon as quasihydrostatic pressure medium agree reasonably well. Using the third-order Birch-Murnaghan equation24 a fit to the volume versus pressure data gives bulk modulus B0 = 58 (2) GPa, its pressure derivative B′0 = 3.6 (1) and volume at zero pressure V0 = 375.1 (9) Å3.
XRD data taken at room temperature in run 2 under pressure up to 62 GPa. Bragg peaks based on the refinement with space group \({\mathrm{R}} \bar{3}{m}\) for 1 GPa data are shown in the tick marks. EuSn2P2 starts transforming into amorphous phase at 34.4 GPa and is in a fully amorphous phase at 36 GPa. Diffraction peaks from Au are identified by asterisks.
PIA has been documented in a wide variety of systems such as ice25, AlPO426,27, SnI428, VO229, and EuIn2As230. The PIA may be related to structural instability violating Born stability criteria28 or related to density/entropy-driven liquid phase25,31. However, the operative mechanism remains an open question in many cases. Additional experimental and computational investigation of variables (charge, orbital, elastic stability) could potentially help to gain a comprehensive understanding of the driving mechanism of PIA in EuSn2P2.
Drastic enhancement of T o
Typical SMS spectra at selected pressures across To are presented in Fig. 3. The SMS spectra were analyzed using CONUSS32 by modeling the data with two sets of hyperfine parameters, magnetic hyperfine field (Hhf) and quadrupole splitting along with sample thickness. In the presence of magnetic ordering, quantum oscillations emerge in the time-domain SMS spectrum due to nuclear Zeeman splitting. The analysis shows that the direction of magnetic hyperfine field is perpendicular to the X-ray propagation direction and lies in the ab-plane at ambient pressure, consistent with the results from neutron diffraction experiments at ambient pressure15. And this direction remains up to 42.7 GPa, the highest pressure reached, indicating Eu spins remain in-plane. When EuSn2P2 is warmed above To, Hhf drops to zero. The periodic oscillations in the data at 16.4 GPa and 96 K indicate a minor oxide impurity phase present in the sample used in run 2, which shows absence of magnetic hyperfine field and can be modeled with two paramagnetic sites with different isomer shift values, one from the sample and another from the impurity phase. In the magnetic phase a small quadrupole splitting of 1–5 mm/s has been included to fit the spectra. The temperature dependence of the extracted magnetic hyperfine field at various pressures is shown in Fig. 4. With increasing pressure, To increases monotonically. It is remarkable that a moderate pressure of 41.2 GPa drives To to 130 K from 30 K at ambient pressure, a more than fourfold enhancement.
Valence state of Eu ions
To provide information on the valence state of Eu ions based on the isomer shift of 151Eu, additional SMS spectra were taken simultaneously from the sample in the diamond anvil cell located inside the cryostat and the Eu2O3 reference placed outside of the cryostat and downstream of sample. The isomer shift is proportional to the electron density (dominated by s electrons) at the nucleus. The large separation of isomer shift values for Eu2+ and Eu3+, resulting from different shielding effect of the closed-shell s-electrons by the 4f 7 and 4f 6 configurations, makes it useful to probe the valence based on the isomer shift value. Figure 5 displays such SMS spectra at various pressures and temperatures as well as corresponding simulated energy-domain spectra showing the changes of the isomer shift values of the sample with increasing pressure and the fixed isomer shift of reference sample Eu2O3. A monotonic increase of isomer shift from −10.3 mm/s at 1.0 GPa, 300 K to −5.39 mm/s at 41.2 GPa, 160 K has been observed (see Table 1). Caution needs to be taken when interpreting the change of isomer shift as change in valence state by simply assuming the contribution solely originating from the change in 4f electrons. For example, in pure Eu metal significant change in isomer shift was observed without obvious change in 4f electron occupancy33.
(Left) Representative SMS spectra of 151Eu from EuSn2P2 in the paramagnetic phase at indicated pressure and temperatures. Eu2O3 is used as reference material to determine the absolute value of the isomer shift and its change with applied pressure. (right) Simulated energy-domain Mössbauer spectra based on the fitting results from each corresponding SMS spectrum. Red shaded lines indicate the isomer shift from the sample and blue lines show the isomer shift of Eu2O3.
To probe the valence state directly, PFY-XAS experiments at Eu’s L3 edge (2p3/2 → 5d transition) were carried out up to 47 GPa. The normalized high-pressure PFY-XAS data are shown in Fig. 6. Eu ions in EuSn2P2 remain mostly divalent up to 19.8 GPa, indicating that the change in isomer shift at lower pressure is largely due to compression effect without involving the 4f electrons. At 19.8 GPa a second absorption peak emerges at ∼8 eV higher in energy and grows with increasing pressure, indicating a transition toward Eu3+. The 8 eV shift corresponds to the excitation energy difference for Eu3+(4f 65d1) and for Eu2+(4f 75d0). Due to the decrease of absorption peak intensity under pressure, it is difficult to estimate the mean valence based on the ratio of the peak intensities. However, combining the PFY-XAS and change in the isomer shift value, it is safe to conclude that Eu take an intermediate valence state above 20 GPa. An accurate evaluation of the valence would require detailed electronic calculations under pressure.
Pressure-enhanced RKKY interaction
The magnetic order in EuSn2P2 at ambient pressure is driven by indirect Ruderman–Kittel–Kasuya–Yosida (RKKY) exchange coupling through spin-polarized conduction band. To provide insight to the enhanced To, we have performed molecular orbital calculations to illustrate the chemical bonding evolution at high pressure. The generated molecular orbitals diagrams containing the degenerated highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) of EuSn2P2 at ambient pressure and 23.3 GPa are shown in Fig. 7. The HOMOs and LUMOs diagrams reflect the orbital interactions just below and above Fermi level, respectively. The blue and red colors indicate the contrast of the orbital symmetry, i.e., antibonding interactions. At both ambient and high pressure, the antibonding characters from Eu-4f orbitals are dominant among intralayer Eu atoms in HOMOs. EuSn2P2 can be viewed as Eu2+ cation packed with (SnP)22− anion along c-axis primarily by ionic bonding interactions from a charge balance view. Specifically, in chemistry Eu and P atoms are bonded ionically, Sn and P atoms are bonded covalently, and Eu and Sn atoms are bonded metallically. Near Fermi level the bonding interaction features can be observed between Eu–Sn and Eu–P at ambient pressure. When pressurized, EuSn2P2 exhibits stronger metallic Eu–Sn bonding interaction and a weaker covalent Sn–Sn bonding feature. Moreover, the distance between Eu–P atoms decreases, likely due to the 3p electronic localization on P induced by pressure. It suggests that pressure-enhanced Eu–Sn bonding interaction contributes to the increasing RKKY interaction and therefore enhanced To. This is consistent with the monotonic decrease of distances of Eu–Sn and Eu–P shown in Fig. 2c. Due to the much shorter intralayer Eu–Eu distance than interlayer Eu–Eu distance which leads to stronger intralayer magnetic exchange interaction than interlayer interaction, it is expected that the enhanced intralayer exchange interaction play a more important role in the increase of To, as concluded in the case of EuIn2As230. In addition, the pressure-induced weakening of the ionic and covalent bonding and enhancement of metallic properties in EuSn2P2 may drive the crystal structure into amorphous phase, similar to amorphous magnets where the magnetic order is maintained in the amorphous phase34.
Band structure calculations
The surface states and spin texture of EuSn2P2 from Eu termination were calculated using the Generalized Gradient approximation (GGA) plus correlation parameter (U = 6 eV) with spin–orbit coupling. According to the calculation, as the pressure is increased, the decreasing atomic distance along ab-plane may influence the topological properties if the in-plane magnetic spin orientation is maintained under pressure (Supplementary Fig. 1). On the other hand, slightly spin canting along c-axis from the Eu layers may change the topological properties completely, consistent with the recent experimental and computational study in EuSn2P235.
Pressure phase diagram
Figure 8 presents the phase diagram constructed by combining the XRD, SMS, and PFY-XAS studies under pressure. The boundary between paramagnetic and magnetic phases is deduced from Fig. 4. To shows a monotonic increase with pressure application with more than four times of the value at ambient pressure. Above 20 GPa a clear slope change in dTo/dP coincides with transition from Eu2+ toward Eu3+ in Eu’s valence based on the PFY-XAS data. Strikingly, magnetic order is found to persist in the amorphous phase at 42.7 GPa. In another topological magnetic material, EuIn2As2, pressure-induced hexagonal-to-amorphous transition has been observed above 17 GPa with absence of magnetic order in the amorphous phase based on electrical resistivity measurements30. The PIA observed in both systems may suggest a similar origin of crystal structure instability. Furthermore, in the crystalline phase of EuIn2As2 a large enhancement of To is attributed to the increase of intraplane exchange interaction, consistent with the enhanced Eu–Sn bond in EuSn2P2.
P–T phase diagram summarizing the pressure-induced amorphous phase transition above 33 GPa, paramagnetic (PM) to magnetic (M) transition, and pressure-induced valence transition from divalent (Eu2+) to intermediate valence state (Eu2 + δ). Solid circles are data points taken in the magnetic phase and open circles are data in the paramagnetic phase.
Discussion
In summary, we have conducted comprehensive studies of crystal structure, magnetic order, and valence state on the magnetic topological semimetal EuSn2P2 under pressure up to 62 GPa. XRD data reveals a rhombohedral-to-amorphous transition at 36 GPa and the amorphous phase remains up to 62 GPa. Pressure enhances the magnetic ordering temperature remarkably with an over fourfold increase from ambient pressure, attributed to the enhancement of RKKY interactions through stronger Eu–Sn bond under pressure. Eu ions remain mostly divalent until 20 GPa and enters an intermediate valence state at higher pressure up to 47 GPa. Band structure calculations in EuSn2P2 show that both change in lattice parameter and change in magnetic configuration from in-plane to out-of-plane will impact the topological properties, with the latter playing a dominant role. The experimentally observed in-plane spin orientation of Eu ions in the measured pressure range suggests that the any possible change of topological properties will be attributed to the change in lattice parameters. Our work establishes that pressure is an effective tuning parameter to elevate the magnetic ordering temperature, a critical parameter to realize novel quantum phases. These rich results pave the way for further experimental and theoretical efforts to explore the pressure-tuning of magnetism, possible superconductivity, and their interplay with crystal structure and topological electronic states.
Methods
XRD
Single crystals of EuSn2P2 were grown by the Sn-flux method reported previously15. High-pressure XRD experiments were carried out at the 13BM-C (PX2) Beamline at the Advanced Photon Source (APS), Argonne National Laboratory (ANL). Two runs of powder XRD experiments at high pressure and room temperature were conducted. X-rays with a wavelength of 0.434 Å were focused to 15 µm (v) × 15 µm (h) size. A piece of single crystalline sample was ground into powder and loaded in the diamond anvil cell. In run 1 a BX90 diamond anvil cell (DAC) equipped with one pair of Boehler-Almax anvils of 500 µm diameter culet to allow large diffraction angles was used36. Helium was used as the pressure-transmitting medium up to 23.3 GPa. Ruby was used to determine pressure37. In run 2 a symmetric cell was used up to 62 GPa with cubic boron nitride seats and anvils of 300 µm diameter culet. Neon pressure-transmitting medium was used. Initial pressure was determined from ruby during neon gas loading and subsequent pressures were determined in situ from the equation of state of Au38 at the same position where XRD data was taken on the sample. In both runs rhenium (Re) gaskets were used to contain the samples between the diamond anvils. The 2-D diffraction images were integrated using DIOPTAS software39 and Rietveld refinements on the XRD data were performed in GSAS-II40.
SMS under pressure
High-pressure 151Eu SMS experiments were carried out at 3ID Beamline of the APS, ANL to investigate the evolution of the magnetism of EuSn2P2. SMS, also known as nuclear forward scattering, utilizes the pulsed synchrotron X-ray to probe the nuclear spin transition in time domain. SMS is a sensitive probe to study magnetic state down to the atomic level and is one of the few techniques compatible with extreme sample environments. The SMS experiments were performed during the standard 24-bunch timing mode of the APS with 153 ns separation between two successive electron bunches for data collection. The magnetism is probed through M1 transition 7/2–5/2 in 151Eu at the nuclear resonant energy of 21.54 keV with high resolution monochromators41. X-rays were focused to 15 µm(v) × 15 µm(h) (FWHM). Low temperatures were achieved in a specially designed helium-flow cryostat42. High pressures were generated using a membrane-driven miniature panoramic DAC. Re gaskets were prepared and EDM-drilled to form the sample chamber.
Three experimental runs were performed with different sample loadings, run 1 up to 10.4 GPa, run 2 up to 22.7 GPa, and run 3 up to 42.7 GPa. A single crystalline sample was loaded in each run such that the incident X-ray is along the c-axis of the crystal. In run 1 and 2 helium was used as pressure medium to ensure hydrostatic pressure environment at low temperatures. In run 3 a neon pressure medium was used. After gas loading at room temperature, all subsequent pressures were applied through gas membrane at low temperature between 100 and 150 K. Pressures were determined from ruby scale37. At each pressure the SMS spectra were collected at various temperatures across the magnetic order. Possible valence transition of Eu ions in the sample can be detected by the change of the isomer shift. The isomer shift values were obtained in situ by placing a reference sample with a known isomer shift value in the X-ray beam33,43,44,45. For divalent Eu ions in EuSn2P2, a trivalent reference sample Eu2O3 with an isomer shift of 1.024 mm/s (relative to EuF3) was placed in the beam. SMS data together with the reference sample were collected in the paramagnetic phase of EuSn2P2 which simplifies the spectra due to the absence of magnetic hyperfine field.
High-pressure PFY-XAS
PFY-XAS experiments were carried out at the 16ID-D Beamline to provide direct information on Eu’s valent state and confirm any possible changes suggested by the isomer shift measurements, XAS experiment was carried out at Eu’s L L3 edge (6.97 keV) up to 47 GPa. A single crystal sample was loaded in a symmetric-type DAC with beryllium gasket and an insert from cubic boron nitride and epoxy. Pressures were measured in situ from ruby fluorescence. To avoid heavy absorption by diamond anvil at this energy, XAS was taken with the incident X-ray beam going through the Be gasket and absorption signal being taken in the fluorescence geometry using a Pilatus detector. The X-rays were focused to 5 µm (FWHM). The sample position at each pressure was carefully determined by scanning the sample position to minimize self-absorption. Ruby was used to determine the pressure in situ37.
Molecular orbital calculations
To provide insight to the enhanced To, we have performed molecular orbital calculations in EuSn2P2 at ambient and high pressure employing semiempirical extended-Hückel-tight-binding methods and CAESAR packages46. The basis sets used in the calculations of molecular orbitals of EuSn2P2 at ambient and high pressure are: 6s: Hii = −7.42 eV, ζ 1 = 1.400, coefficient1 = 1.0000; 6p: Hii = −4.65 eV, ζ 1 = 1.400, coefficient1 = 1.000; 5d: Hii = −8.08 eV, ζ 1 = 2.753, coefficient1 = 0.7187, ζ 1 = 1.267, coefficient2 = 0.4449; 4 f: Hii = −11.28 eV, ζ 1 = 6.907, coefficient1 = 0.7354, ζ 1 = 2.639, coefficient2 = 0.4597. For Sn: 5s: Hii = −16.16 eV, ζ 1 = 2.120, coefficient1 = 1.000; 5p: Hii = −8.32 eV, ζ 1 = 1.820, coefficient1 = 1.000. For P: 3s: Hii = −18.60 eV, ζ 1 = 1.750, coefficient1 = 1.000; 3p: Hii = −14.00 eV, ζ 1 = 1.300, coefficient1 = 1.000.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
He, M., Sun, H. & He, Q. L. Topological insulator: spintronics and quantum computations. Front. Phys. 14, 43401 (2019).
Tokura, Y., Yasuda, K. & Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 1, 126–143 (2019).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Masuda, H. et al. Quantum Hall effect in a bulk antiferromagnet EuMnBi2 with magnetically confined two-dimensional Dirac fermions. Sci. Adv. 2, e1501117 (2016).
Deng, Y. et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 367, 895–900 (2020).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B. 81, 245209 (2010).
Li, R., Wang, J., Qi, X.-L. & Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284–288 (2010).
Otrokov, M. M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416–422 (2019).
Zhang, D. et al. Topological Axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric. Phys. Rev. Lett. 122, 206401 (2019).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Chiral topological superconductor from the quantum Hall state. Phys. Rev. B 82, 184516 (2010).
Hao, Y.-J. et al. Gapless surface Dirac cone in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 9, 041038 (2019).
Li, J. et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 5, eaaw5685 (2019).
Chen, B. et al. Intrinsic magnetic topological insulator phases in the Sb doped MnBi2Te4 bulks and thin flakes. Nat. Commun. 10, 4469 (2019).
Gui, X. et al. A new magnetic topological quantum material candidate by design. ACS Cent. Sci. 5, 900–910 (2019).
Wang, L. L. et al. Single pair of Weyl fermions in the half-metallic semimetal EuCd2As2. Phys. Rev. B 99, 245147 (2019).
Li, H. et al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 9, 041039 (2019).
Xu, Y., Song, Z., Wang, Z., Weng, H. & Dai, X. Higher-order topology of the Axion insulator EuIn2As2. Phys. Rev. Lett. 122, 256402 (2019).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Ōnuki, Y. et al. Divalent, trivalent, and heavy fermion states in Eu compounds. Philos. Mag. 97, 3399–3414 (2017).
Rosa, P. F. S. et al. Competing magnetic orders in the superconducting state of heavy-fermion CeRhIn5. Proc. Natl Acad. Sci. U.S.A. 114, 5384–5388 (2017).
Wu, J. J. et al. Pressure-decoupled magnetic and structural transitions of the parent compound of iron-based 122 superconductors BaFe2As2. Proc. Natl Acad. Sci. U.S.A. 110, 17263–17266 (2013).
Zhao, L. et al. Monoclinic EuSn2As2: a novel high-pressure network structure. Phys. Rev. Lett. 126, 155701 (2021).
Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300°K. J. Geophys. Res. 83, 1257–1268 (1978).
Bauer, R., Tse, J. S., Komatsu, K., Machida, S. & Hattori, T. Slow compression of crystalline ice at low temperature. Nature 585, E9–E10 (2020).
Sankaran, H., Sharma, S. M., Sikka, S. K. & Chidambaram, R. Pressure induced amorphization of AlPO4. Pramana 35, 177–180 (1990).
Tse, J. S. & Klug, D. D. Structural memory in pressure-amorphized AlPO4. Science 255, 1559–1561 (1992).
Liu, H. et al. Mechanisms for pressure-induced crystal-crystal transition, amorphization, and devitrification of SnI4. J. Chem. Phys. 143, 164508 (2015).
Wang, Y. et al. Reversible switching between pressure-induced amorphization and thermal-driven recrystallization in VO2(B) nanosheets. Nat. Commun. 7, 12214 (2016).
Yu, F. H. et al. Elevating the magnetic exchange coupling in the compressed antiferromagnetic axion insulator candidate EuIn2As2. Phys. Rev. B 102, 180404 (2020).
Deb, S. K., Wilding, M., Somayazulu, M. & McMillan, P. F. Pressure-induced amorphization and an amorphous - amorphous transition in densified porous silicon. Nature 414, 528–530 (2001).
Sturhahn, W. CONUSS and PHOENIX: evaluation of nuclear resonant scattering data. Hyperfine Interact. 125, 149–172 (2000).
Bi, W. et al. Synchrotron x-ray spectroscopy studies of valence and magnetic state in europium metal to extreme pressures. Phys. Rev. B 85, 205134 (2012).
Coey, J. M. D. Amorphous magnetic order. J. Appl. Phys. 49, 1646–1652 (1978).
Pierantozzi, G. M. et al. Evidence of magnetism-induced topological protection in the axion insulator candidate EuSn2P2. Proc. Natl Acad. Sci. 119, e2116575119 (2022).
Kantor, I. et al. BX90: A new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 83, 125102 (2012).
Dewaele, A., Torrent, M., Loubeyre, P. & Mezouar, M. Compression curves of transition metals in the Mbar range: Experiments and projector augmented-wave calculations. Phys. Rev. B. 78, 104102 (2008).
Fei, Y. et al. Toward an internally consistent pressure scale. Proc. Natl Acad. Sci. 104, 9182–9186 (2007).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res. 35, 223–230 (2015).
Toby, B. H. & Von Dreele, R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 46, 544–549 (2013).
Leupold, O. et al. Nuclear resonance scattering of synchrotron radiation at the 21.5 keV resonance of 151Eu. Europhys. Lett. 35, 671–676 (1996).
Zhao, J. Y. et al. A compact membrane-driven diamond anvil cell and cryostat system for nuclear resonant scattering at high pressure and low temperature. Rev. Sci. Instrum. 88, 125109 (2017).
Wortmann, G., Ponkratz, U., Bielemeier, B. & Rupprecht, K. Phonon density-of-states in bcc and hcp Eu metal under high pressure measured by 151Eu nuclear inelastic scattering of synchrotron radiation. High. Press. Res. 28, 545–551 (2008).
Souza-Neto, N. M. et al. Reentrant valence transition in EuO at high pressures: beyond the bond-valence model. Phys. Rev. Lett. 109, 026403 (2012).
Bi, W. et al. Microscopic phase diagram of Eu(Fe1-xNix)As2 (x = 0,0.04) under pressure. Phys. Rev. B 103, 195135 (2021).
Hoffmann, R. An extended hückel theory. I. Hydrocarbons. J. Chem. Phys. 39, 1397–1412 (1963).
Acknowledgements
We thank G. Fabbris for critical reading of the manuscript and helpful discussion. This work is supported by the National Science Foundation (NSF) through Grant No. OIA-2033131. T.C. acknowledges the support provided by the National Aeronautics and Space Administration (NASA)-Alabama Space Grant Consortium, Research Experiences for Undergraduates (REU) award to University of Alabama at Birmingham. Z.N. acknowledges the support from the Department of Education-Graduate Assistantship in Areas of National Need (GAANN) Grant No. P200A180001. W.X. is supported by Department of Energy under the contract of DE-SC0022156. This research used resources of the Advanced Photon Source (APS), Argonne National Laboratory (ANL), a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE- AC02-06CH11357. Portions of this work were performed at HPCAT (Sector 16), APS, ANL. HPCAT operations are supported by DOE-NNSA’s Office of Experimental Sciences. B.L., COMPRES-GSECARS gas loading system, and the PX2 program are supported by COMPRES under NSF Cooperative Agreement EAR-1606856. We are grateful to S. Tkachev for help with the gas loading of the DACs at the APS.
Author information
Authors and Affiliations
Contributions
W.B. designed this research project. W.B., T.C., Z.N., J.Z., B.L., E.E.A, D.Z, J.X., Y.X., and Y.K.V. performed the experiments. W.X. synthesize the EuSn2P2 sample and performed the molecular orbital calculations. H.-J.T. and T.-R.C. conducted the GGA calculations. W.B., T.C., and U.D. analyzed the data. W.B. and W.X. wrote the paper with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bi, W., Culverhouse, T., Nix, Z. et al. Drastic enhancement of magnetic critical temperature and amorphization in topological magnet EuSn2P2 under pressure. npj Quantum Mater. 7, 43 (2022). https://doi.org/10.1038/s41535-022-00451-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00451-9
This article is cited by
-
Origin of the exotic electronic states in antiferromagnetic NdSb
npj Quantum Materials (2023)