Introduction

The link between quantum criticality and the emergence of unconventional superconducting (SC) states is ubiquitous among several families of materials including heavy fermion, cuprates, and iron-based (Fe SC) superconductors1,2,3. The presence of divergent critical fluctuations associated to a nearby order are thought to provide a pairing glue and significantly enhance the SC transition temperature4,5. Dating from the seminal work of Berk and Schrieffer6, most studies have been devoted to fluctuations near a magnetic instability, and in particular antiferromagnetic (AF) ones which give rise to non s-wave pairing states such as d-wave in the cuprates, and possibly in heavy fermion and organic SC7.

In many Fe SC, SC emerges on the border of an AF state that is, however, also accompanied, or even preceded, by an electron nematic phase whereby the electron fluid spontaneously breaks the fourfold rotational symmetry of the underlying tetragonal lattice8,9. The initial focus was on the proximity of the AF phase which is expected to lead a sign changing s± SC pairing state10,11, but recently the role of nematic fluctuations and criticality on the SC state has come under scrutiny12,13,14,15,16,17,18,19,20. Several theoretical works have argued that the SC pairing is generically enhanced near a nematic quantum critical point (QCP)5,21,22,23,24, even if it is not the leading pairing glue. On the experimental side, disentangling the role of AF and nematic QCP has proved challenging because the associated orders are essentially concomitant in most Fe SC. An exception is FeSe, where at ambient pressure SC emerges at about 8 K out of a nonmagnetic nematic state that sets in at much higher temperature ~90 K25,26. The origin of the nematic state in FeSe is currently under debate, with both orbital and spin degrees of freedom possibly playing a role27,28,29,30,31. Weakening the nematic order in order to reach a putative QCP can in principle be achieved by either physical or chemical pressure. In the case of hydrostatic pressure, a magnetic order sets in before the end point of the nematic phase precluding a nematic QCP32,33,34,35. By substituting selenium (Se) with isovalent sulfur (S), however, the nematic order can be continuously suppressed without any magnetic order15,36,37 (see Fig. 1a), providing a model system to study the impact of a nematic QCP on SC and normal state properties.

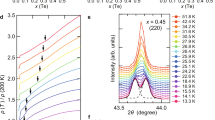
Fig. 1: Raman spectra in the B1g nematic channel of FeSe1−xSx.
figure 1

a Phase diagram of FeSe1−xSx. The arrows indicate the compositions whose Raman spectra are shown in (b). b Raman response as a function of temperature in B1g symmetry channel for five different sulfur compositions. The energy is shown on a logarithmic scale. The quasi-elastic peak (QEP) and high-energy peak (HE) are indicated by arrows in the x = 0 spectra.

Full size image

Several studies indicate a significant impact of the nematic order on the SC pairing state38,39,40,41. However, intriguingly the evolution of Tc in FeSe1−xSx indicates a marginal role for nematic quantum critical fluctuations in boosting SC. In fact coming from the tetragonal, non-nematic side of the FeSe1−xSx phase diagram, Tc is essentially flat upon approaching the nematic QCP at xc ~ 0.17 showing only a mild maximum well-inside the nematic ordered phase42,43 (Fig. 1a). This apparent contradiction with theoretical expectations was recently argued to arise from the coupling between electronic nematic degrees of freedom and the lattice, which cuts off nematic quantum criticality at low temperature. This effect may suppress the expected enhancement of Tc found in electronic-only models24. The lattice may also play a significant role in restoring Fermi liquid behavior of the normal state near the QCP44,45,46. In general, the effect of the lattice appears to have been overlooked in several previous studies of the nematic QCP FeSe1−xSx15,47, calling for an experimental clarification of its potential role in the properties of FeSe1−xSx near the nematic end point.

Here we use the ability of Raman scattering to probe symmetry resolved electronic fluctuations in the long wavelength limit (q = 0)48,49,50,51,52,53,54,55 to investigate the evolution of nematic fluctuations in FeSe1−xSx as a function of doping and temperature. Our study spans a significant portion of the phase diagram of FeSe1−xSx, from x = 0 to x = 0.27. This allows us to assess the evolution of critical nematic fluctuations across the nematic QCP, located at xc ~ 0.1739,42. The dynamical nematic fluctuations spectrum consists of two main components, but only one of them shows a clear critical behavior upon approaching the nematic phase transition. A Curie–Weiss analysis of the critical component reveals a significant shift between the bare electron-only nematic QCP that is captured by Raman scattering, and the thermodynamic one. We attribute this shift to electron–lattice coupling, whose energy scale is found to be a sizable fraction of the typical Fermi energy of S–FeSe, and may explain the absence of Tc enhancement at the nematic QCP. Our study highlights the important role of electron–lattice coupling effects in both SC and normal state properties of FeSe, and more generally of Fe SC.

Results

Sulfur doping dependence of symmetry-resolved Raman spectrum

In our study, seven different sulfur (S) compositions x were studied. The S content of the studied single crystals, which usually differs significantly from the nominal one, was determined by element-specific energy dispersive X-ray spectroscopy (EDS) and single-crystal X-Ray Diffraction (XRD) measurements (see “Methods”). The structural/nematic transition Ts was determined by transport measurements on crystals from the same batch, and also in situ via the observation of the onset of elastic light scattering by nematic domain formation below Ts (see Supplementary Fig. 1). Tc was determined by the onset of diamagnetic signal in SQUID magnetometry. The phase diagram in Fig. 1 summarizes the properties (x, Ts, Tc) of the crystals studied. Details on the Raman scattering measurements can be found in the “Methods” section.

In Fig. 1b, we show the temperature dependence of the electronic Raman scattering spectrum for five different dopings (x = 0, x = 0.07(2), x = 0.14(2), x = 0.22 (2) and x = 0.27 (2)) over a relatively wide energy range (0–2000 cm−1, corresponding to 0–250 meV). Data for x = 0 (FeSe) were already reported in52. Incoming and outgoing photon polarizations were oriented so as to probe the B1g symmetry channel (using the 1 Fe unit cell notation), which transforms as x2 − y2 and thus corresponds to the nematic order parameter symmetry (see “Methods”). For all compositions, two main features, marked by arrows in the x = 0 spectra, can be distinguished: a relatively broad peak at high energy (hereafter labeled HE peak) located at around 400 cm−1 (50 meV), and a narrower feature, a quasi-elastic peak (QEP), located at much lower energy, below 100 cm−1 (~12 meV) at low temperatures. The low x content data are consistent with a previous Raman study which reported data in a more limited spectral and doping range56 (see Supplementary Discussion for a comparison between the present work and ref. 56). The HE peak intensity decreases with doping (see also Fig. 2) and is only mildly affected by Ts. The QEP by contrast is strongly affected by Ts and displays a significant doping and temperature dependence: its intensity is maximum close to Ts for lower x compositions, and continuously increases down to the lowest measured temperature (17 K) for x = 0.22. The enhancement and collapse of the QEP across the nematic/structural transition temperature is consistent with previous studies in various Fe SC49,51,52,55 and is ascribed to critical nematic fluctuations near Ts. The QEP intensity is significantly reduced for x = 0.27 (see Figs. 1b and 2) indicating a reduction of nematic fluctuations for high x content. Figure 2 shows the symmetry dependence of the QEP and HE peak: consistent with the nematic fluctuations interpretation, the QEP is absent in both B2g and A1g channels throughout the compositional range studied. Interestingly, the HE peak displays a robust symmetry dependence: it is observed only in the B1g channel for all x.

Fig. 2: Symmetry dependence of the Raman spectra.
figure 2

a Low energy part (on a linear scale) of the Raman spectra for two different symmetry channels B1g (full lines) and A1g + B2g (dotted lines) and for x = 0.07, x = 0.14, x = 0.22, and x = 0.27. b symmetry channel dependence of the spectra over a wide energy range on a linear scale for x = 0, x = 0.07, and x = 0.27.

Full size image

Extracting critical nematic fluctuations

In order to analyze in more details the two main components of the nematic fluctuation spectrum, we performed a two component fit of the Raman spectra, where the QEP and HE peaks are fitted by an overdamped Lorentzian and a damped oscillator, respectively. \(\chi ^{\prime\prime} (\omega )=A\frac{\omega {{{\Gamma }}}_{{\rm{QEP}}}}{{\omega }^{2}+{{{\Gamma }}}_{{\rm{QEP}}}^{2}}+B\frac{\omega {\omega }_{{\rm{HE}}}^{2}{{{\Gamma }}}_{{\rm{HE}}}}{{(\omega {{{\Gamma }}}_{{\rm{HE}}})}^{2}+{({\omega }^{2}-{\omega }_{{\rm{HE}}}^{2})}^{2}}\). A small linear background was added to model the high energy part of the spectra. We discuss the possible origin the HE peak below. The overdamped functional form taken for the QEP can be linked to a Drude-like Raman response of itinerant carriers that is renormalized near a nematic instability. In this framework, ΓQEP is an effective quasiparticle scattering rate where the impurity scattering rate Γ0 in the B1g channel is renormalized by the nematic correlation length ξn: ΓQEP = \({{{\Gamma }}}_{0}{(\frac{a}{{\xi }_{n}})}^{2}\) where a is the lattice parameter of the Fe plane50,57,58. We note that an alternative description in terms of coupling of itinerant carriers to finite momentum stripe-like spin-nematic fluctuations via Aslamasov–Larkin processes yields essentially the same functional lineshape for the QEP, making it difficult to conclude on the exact mechanism of the QEP59,60,61. The two approaches differ in the way the Raman probe couples to nematic degrees of freedom, but they both associate the QEP to the response to itinerant carriers near a nematic instability. On the other hand, the QEP lineshape cannot be accounted by theories of the Raman response based on local spin physics alone62.

As shown in Fig. 3a (see Supplementary Fig. 3 for more doping and temperatures), all the spectra below ~ 150 K could be reproduced with this decomposition. At higher temperatures, the QEP and HE essentially merge, making it difficult to unambiguously separate them via the fitting procedure. The HE peak energy was found to be weakly dependent of doping and temperature, but its width ΓHE displays a marked decrease below Ts (see Supplementary Fig. 5). From the decomposition, we can extract the behavior of the static nematic susceptibility χ0 associated to each component (Fig. 3b). Indeed using Kramers–Kronig relations, we have: \({\chi }_{0}^{{\rm{QEP}}}=\mathop{\int}\nolimits_{0}^{\infty }\frac{\chi ^{\prime\prime} }{\omega }d\omega\) = A and equivalently \({\chi }_{0}^{{\rm{HE}}}\) = B. For all dopings the QEP component is the dominant contribution to the nematic susceptibility. Besides, as shown in Fig. 3b, the QEP component is significantly more critical than the HE component (see also Supplementary Fig. 7). An exception is x = 0.27 where both contributions display a similar mild temperature dependence. This points to two distinct sources of nematic fluctuations in FeSe, with one displaying a more critical behavior near the nematic QCP.

Fig. 3: Two component analysis of the nematic fluctuation spectrum.
figure 3

a Decomposition of the B1g Raman response illustrated at three different compositions: x = 0, x = 0.14, and x = 0.27 (see equation in the main text). The QEP peak component is highlighted via shading. b Temperature dependence of the two main contributions (QEP and HE) to the static nematic susceptibility χ0. Standard errors of the fits are shown but are usually smaller than the symbols.

Full size image

We note that a different decomposition of the Raman response of FeSe was proposed in56, where a gap-like suppression was added in order to reproduce the loss of intensity of the spectra at low energy in B1g symmetry below Ts. The gap opening was interpreted as the consequence of a modulated orbital order. In our case, we found that the spectra across Ts could be well reproduced without invoking a gap. Rather the apparent spectral gap below Ts results in our case from a combination of the collapse of the QEP contribution in the nematic phase and a sizable reduction of the width of the HE peak. The HE peak being present at all doping and temperatures we do not believe it is associated to the modulated orbital order conjectured in56. A suppression of the nematic fluctuations, and thus the QEP, is qualitatively expected in the nematic ordered phase. Still the strong suppression of the QEP observed could also be reinforced by an orbital transmutation effect below Ts, whereby the hole pocket becomes essentially single component in orbital space inducing strong vertex corrections that further suppress the B1g Raman response in the nematic phase57.

Focusing now on the critical behavior of the QEP component, we display in Fig. 4a \(\frac{1}{{\chi }_{0}^{{\rm{QEP}}}}\) as a function of x and T. We have added two additional compositions where spectra were taken in a more limited spectral range, allowing only the extraction of the QEP component (see Supplementary Fig. 4). Assuming a mean-field Curie–Weiss temperature dependence, we can extract the corresponding nematic Curie–Weiss temperature T0 whose x dependence is shown in Fig. 4b. We note that a Curie–Weiss temperature dependence does not necessarily imply that local nematic degrees of freedom are assumed. Indeed, it has been shown both in the context of itinerant magnetism and electronic nematicity that susceptibilities following Curie–Weiss law can be obtained even in purely itinerant but interacting electron models30,63. The evolution of T0 extracted directly from the raw data using Kramer–Kronig relations restricted to energies below 400 cm−1 (labeled \({T}_{0}^{400{\rm{cm}}^{-1}}\)) is also shown for comparison (see Supplementary Fig. 6). While less transparent, this determination has the advantage of not relying on any assumption about the functional form of the low energy part of the spectrum. Consistently with low energy QEP part of the B1g spectrum being more critical, \({T}_{0}^{400{\rm{cm}}^{-1}}\) tend to be lower than \({T}_{0}^{{\rm{QEP}}}\) determined from the QEP part only. Note also that even lower T0 are obtained if the full temperature dependent part of the spectra, thus including both QEP and HE contributions to χ0, is integrated from 0 to 2000 cm−1 (see Supplementary Figs. 6 and 8). Since our focus is on the impact of nematic criticality on low energy physics which governs both SC and transport, we believe that it is the behavior of the low energy critical QEP that is the most relevant for the present discussion. Therefore we restrict our discussion to \({T}_{0}^{{\rm{QEP}}}\) and \({T}_{0}^{400{\rm{cm}}^{-1}}\) below.

Fig. 4: Curie–Weiss analysis of the critical nematic susceptibility.
figure 4

a Curie–Weiss analysis of the critical inverse nematic susceptibility component \({\chi }_{0}^{{\rm{QEP}}}\). Note that only data above Ts are shown for low x compositions. b Phase diagram x − T of FeSe1−xSx showing the evolution of the Curie–Weiss nematic transition temperature T0 extracted from the analysis in (a) (full square). The error bars for T0 correspond to standard errors of the Curie–Weiss fits. Also shown in open squares are the T0 values extracted from a Curie–Weiss analysis of the χ0 extracted without any fitting by performing a Kramers–Kronig integration of the raw data restricted to energies below 400 cm−1 (see Supplementary Fig. 6). The lines are linear fits of T0 (x) values.

Full size image

For both determinations, T0 decreases with x tracking Ts but stays significantly below it (Fig. 4b). The difference between Ts and T0 is a consequence of the finite electron–lattice coupling as first discussed by Kontani and Yamakawa64. Because the nematic susceptibility χ0 extracted from Raman spectra is in the dynamical limit (k = 0 and then ω = 0, while the opposite is required for a thermodynamical susceptibility), the symmetry allowed coupling between electronic nematic fluctuations and the soft orthorhombic acoustical phonon vanishes, leaving only the contribution from the bare electronic-only nematic susceptibility50. In this picture, T0 represents the mean-field nematic transition temperature in the absence of the lattice. By contrast in the opposite thermodynamical or static limit, the electron–lattice comes into play and stabilizes the nematic transition at Ts > T0. We note that such a picture was validated by comparing the temperature dependence of the Raman nematic susceptibility and the shear modulus in both Ba(Fe1−xCox)2As2 and FeSe1−xSx50,52. In FeSe1−xSx, the difference between Ts and T0 is significant for the four compositions showing nematic order, ranging from 45 to 75 K, depending on the method used to extract T0. An unavoidable consequence of this large difference is a significant difference in the location of the associated critical points: the bare electronic nematic QCP extrapolates at \({x}_{{\rm{QCP}}}^{0} \sim 0.07(\!\pm 0.04)\), but the thermodynamical QCP is located at xQCP ~ 0.17 (±0.02). We stress that the bare nematic QCP is only fictitious. Still, its location is paramount since as we discuss below, it ultimately governs the impact of the critical nematic fluctuations on low energy properties such as SC pairing and transport lifetime.

Discussion

As stated above, the x evolution of T0 points to a significant impact of lattice effects on nematic QCP physics. In order to quantify it, we introduce the ratio r0 = \(\frac{{k}_{{B}}({T}_{{s}}-{T}_{0})}{{E}_{{F}}}\) where EF is the Fermi energy44. r0 = 0 signifies the absence of shift of the QCP. On the other hand, r0 ~ 1 indicates a strong impact of the lattice on the QCP that can manifest itself by, e.g., a restoration of Fermi liquid behavior above the QCP44,46. For pure FeSe, the hole and electron pocket are small, resulting in small EF of about 20 meV for each xz/yz-derived electron pockets according to ARPES42. Adding S only results in the appearance of a small inner-hole pocket above EF, but does not change appreciably the size of the other pockets, at least below x ~ 0.17. Taking 20 meV as an upper bound for EF for all FeSe1−xSx, we plot r0 versus Ts as shown in Fig. 5. Despite some scatter in the values of r0, the plot suggests a significant value of r0 extrapolated at the thermodynamic QCP where Ts = 0: from r0 = 0.35 ± 0.15. Also shown in Fig. 5 are values for Ba122 which are reduced compared to FeSe1−xSx, but still significant (~0.2).

Fig. 5: Lattice-shifted nematic quantum criticality.
figure 5

Dimensionless nemato-electron–lattice coupling r0 = \(\frac{{k}_{{B}}({T}_{s}-{T}_{0})}{{E}_{{F}}}\) as a function of Ts for FeSe1−xSx and Ba(Fe1−xCox)2As250. The Fermi energy EF was taken to be 20 and 40 meV for FeSe1−xSx and Ba(Fe1−xCox)2As2, respectively. For FeSe, full (empty) circles correspond to r0 values deduced from \({T}_{0}^{\rm{QEP}}\) (\({T}_{0}^{400{\rm{cm}}^{-1}}\)). By definition the origin of the graph corresponds to the location of the QCP in the absence of any coupling to the lattice (Ts = T0), the arrows illustrate the effect of the lattice on the QCP. The line is linear fit of r0 (Ts) used to deduced r0 (Ts = 0), and the filled ovals illustrate their associated uncertainties.

Full size image

Next, we discuss the consequences of our findings for the SC near the nematic QCP of FeSe1−xSx. Theoretical works that ignored nemato-elastic coupling have argued that near a nematic QCP, the critical nematic fluctuations can lead to a boost in the SC Tc. On the other hand, once this coupling is taken into account it leads to a crossover Fermi liquid temperature scale TFL = \({r}_{0}^{3/2}{E}_{{F}}\) below which the critical nematic fluctuations are suppressed44. In the case of S–FeSe, we estimate TFL ~ 55 (±25) K. Since TFL > Tc ~ 10 K in this system, it is unlikely that the critical nematic fluctuations play a role in the pairing in FeSe1−xSx. For such a situation Labat et al.24 found that significant Tc enhancement at the QCP occurs only if the nemato-elastic coupling is weak enough such that r0 < (U/V)2, where U is an effective interaction in the nematic channel and V is an effective SC pairing attraction due to, e.g., spin fluctuations. For Fe SC, we expect V > U since pairing is dominated by spin fluctuations away from QCP. While there is currently no realistic theoretical evaluation of V and U for FeSe, since in practice no Tc boost has been noted in S–FeSe, we conclude that the nemato-elastic coupling is significantly large with r0 > (U/V)2.

The same analysis applied to Ba(Fe1−xCox)2As2 gives TFL ~ 40 (±10) K, much closer to the actual Tc observed in these systems. The above estimate suggests that Ba122 systems may be more promising candidates for a significant effect of the nematic QCP on Tc. While the presence of a nearby magnetic QCP in most Ba122 complicates the matter, we note the recent observation of a significant enhancement of Tc near a nematic QCP in Ba1−xSrxNi2As2 in the absence of any magnetic order19. Interestingly, band structure calculations predict a much larger Fermi surface and therefore a larger EF with respect to BaFe2As265. This may possibly lead to a significantly reduced r0, and thus much weaker lattice effects on the QCP of Ba1−xSrxNi2Fe2. Further investigations, in particular nematic susceptibility measurements, are needed to assess the electron–lattice coupling in this system and confirm this scenario.

Finally, we address the origin the noncritical HE peak component observed in the B1g spectrum. As discussed above, it only appears in the B1g nematic channel and its energy, around 400 cm−1 (50 meV), is only mildly temperature and x dependent. A first possible interpretation is that it comes from interband transitions between the two hole bands centered at the Γ point which are split by spin-orbit coupling57. In that case, however, we would expect the energy of the HE peak to be very close to the spin-orbit induced energy splitting57, which is estimated from ARPES measurements to be 20 meV36, significantly below 50 meV. In addition, simple calculations of the interband Raman spectrum indicate that it should appear in both B1g and B2g symmetries with comparable intensity, again in disagreement with experiments (see Supplementary Note for Raman calculations of the contribution of interband transitions in the presence of spin-orbit coupling). This leads us to conclude that the HE peak is unlikely of interband origin.

As first argued by Baum et al.62 (see also66), the HE peak more likely arises from spin fluctuations associated to local moments. Local moments have been argued to be relevant for Fe SC due to Hund’s coupling physics67,68,69,70, where electrons have both itinerant and localized, or “Janus face,” character. Numerical calculations of the Raman response within a spin-1 Heisenberg localized spin model with bi-quadratic interactions with exchange parameters believed to be adequate for FeSe have indeed shown the presence of a paramagnon peak in the B1g symmetry channel. Compared to two magnon excitations of ordered antiferromagnets, in FeSe the paramagnon is pushed below typical exchange energies due to magnetic frustration and the presence of both stripe-like and Néél-like AF fluctuations71. The presence of low-lying paramagnon excitations in FeSe has been confirmed by resonant inelastic X-ray scattering (RIXS) measurements, where a dispersive collective mode was observed, and interpreted as a paramagnon excitation72. The energy of the RIXS paramagnon peak near the zone center is close to 50 meV, similar to the Raman HE peak, further enforcing the interpretation of the HE peak in terms of local spin physics. We note that within the Fleury–Loudon formalism of Raman scattering in insulating magnets with nearest neighbors exchange, the B1g Raman scattering operator for spin 1/2 is equivalent to the spin-nematic order parameter written in real space \({O}_{{B}_{\rm{1g}}}\) = Px − Py where Pα = ∑rSr. Sr+α73. For spin 1 systems with bi-quadratic couplings, higher-order terms such as spin quadrupole will also come into play, and may contribute to the B1g HE peak too74,75. If interpreted along these lines, the nematic susceptibility extracted from the HE component can be interpreted as the local spin-nematic component of the nematic susceptibility.

In conclusion, the picture emerging from these considerations is that of two distinct component in the nematic fluctuations spectrum in FeSe: one associated with itinerant carrier and displaying clear critical behavior as embodied by \({\chi }_{\rm{QEP}}^{0}\), and the other associated more correlated electrons and local moment physics which, while sizable, is less critical as observed for \({\chi }_{\rm{HE}}^{0}\). This suggests that the nematic instability is driven mainly by itinerant carriers. However, as we have shown the coupling of these fluctuations to the lattice most likely prevent them from playing a role in enhancing Tc near the nematic QCP of FeSe1−xSx. Other Fe SC systems with weaker nemato-elastic coupling, but ideally no other ordering, may provide a better platform to demonstrate this effect. Another open question is whether the local spin component has a role in the SC instability in FeSe. Our work suggests that this “Janus face” aspect of nematicity might be a generic feature of Hund’s metals like FeSe.

Methods

Raman experiments

Raman experiments have been carried out using a triple grating JY-T64000 spectrometer. Spectra below 500 cm−1 were obtained using subtractive mode and 1800 grooves/mm gratings. High-energy spectra between 50 and 2500 cm−1 were obtained using a single stage spectrometer with a 600 grooves/mm grating and long-pass edge filter to block the stray light. The spectrometer were equipped with a nitrogen cooled back illuminated CCD detector. All measurements were performed using the 532 nm excitation line from a diode pump solid-state laser. Measurement in B1g symmetry channels was obtained using cross-incoming and -outgoing linear polarization oriented at 45 degrees of the Fe–Fe bonds, while A1g + B2g channel was obtained using parallel polarization at 45 degrees of the Fe–Fe bonds. For several x complimentary, measurements were performed in the B2g symmetry channel using cross polarization along the Fe–Fe bonds. The laser heating was estimated in situ by tracking the onset of elastic light scattering by orthorhombic domains across Ts at different laser powers for x = 0, x = 0.05, and x = 0.14 single crystals, yielding 1 K/mW (±0.2) for all samples52. This value was taken for all the other samples. All the raw spectra have been corrected for the Bose factor and the instrumental spectral response. They are thus proportional to the imaginary part of the Raman response function χ″ (ω, T) in the corresponding symmetry channel. In order to compute the nematic susceptibility using Kramers–Kronig relation, the Raman susceptibility was interpolated from the lowest wavenumber measured (10 cm−1) to 0 using the QEP lineshape described in the main text.

Samples

The x = 0 crystal was grown in Grenoble using the chemical vapor transport method based on the use of an eutectic mixture of AlCl3/KCl as described in76. The x = 0.05, x = 0.07, x = 0.14, x = 0.17, and x = 0.22 single crystals were grown in Tohoku University by the molten salt flux methods77. Polycrystalline FeSe1−xSx for the single-crystal growth precursors were synthesized by the solid-state reaction methods78. Polycrystalline FeSe1−xSx and KCl/AlCl3 were mixed up inside the Ar grove box with the molar ratio of 1:12 and were sealed in the quartz tube under the vacuum condition of 10−2 Pa. The quartz ampoule was heated using the tube furnace. The temperature of hot and cold positions was kept at 390 °C and 240 °C, respectively. After ~10 days, single crystals were grown around the cold part of the quartz tube. The x = 0.27 crystal was grown in Ames out of an eutectic mix of KCl/AlCl3 salts as described in79. Details about the growth and characterization of x = 0.27 single crystals from the same batch can also be found in43. Single crystals from the same batch were characterized by transport measurements yielding first estimates of Ts and Tc. The measured crystals were further characterized by SQUID magnetometry to obtain their Tc, by EDS and XRD to obtain their sulfur content x.

XRD data on FeSe1−xSx single crystals were collected at 295 K on a STOE imaging plate diffraction system (IPDS-2T) using Mo Kα radiation. All accessible symmetry-equivalent reflections (≈4500) were measured up to a maximum angle of 2Θ = 65 deg. The data were corrected for Lorentz, polarization, extinction, and absorption effects. Using SHELXL80 and JANA200681, around 101 averaged symmetry-independent reflections (I > 2σ) have been included for the refinements in space group P4/nmm. The refinements converged quite well and the somewhat increased reliability factors (see GOF, R1, and wR2 in the Table) and uncertainties for the atomic positions and the ADPs result from the significant mosaic spread often observed for FeSe1−xSx samples. Results for x = 0.12, 0.22, and 0.27 are shown in Supplementary Table 1 as representatives.

In general, both EDS and X-ray yielded consistent results within 20% for x except for the highest S content x = 0.27. We note that EDS is only a semi-quantitative measure of x unless the element-specific X-ray yield is quantitatively calibrated for the given instrument. Therefore XRD data were trusted in most case, except for x = 0.14 where the value of Ts under the laser spot (25 K) indicates a slightly higher S content than the XRD value (x = 0.12 (3)).

In addition, Ts was estimated in situ on the same single crystals by monitoring the onset for elastic light scattering by orthorhombic domains at very small powers (0.1 mW) for x = 0, x = 0.05, and x = 0.14. Except for x = 0.07, Ts value quoted in the text were extracted from this method. For x = 0.07, transport value from samples from the same batch was taken (see Supplementary Fig. 1).