Abstract
The spin dynamics of {Cr8Y8}, a rare example of ferromagnetic molecular rings, has been studied by inelastic neutron scattering (INS) and heat capacity (HC) methods. Clear evidence of low-lying magnetic excitation has been found. Magnetic Schottky anomalies are observed in low-temperature (low-T) HC curves measured under various fields and can be well fitted with a multi-level Schottky term, giving important information on the energy gaps between spin levels. The INS results obtained on TOFTOF and NEAT time-of-flight spectrometers show INS peaks corresponding to the transitions within S = 12 ground states and between the S = 12 ground state and the S = 11 excited state. The single-J model with a unique exchange constant J = 0.151 meV can well reproduce the low-lying energy levels and their Zeeman splitting upon applied magnetic fields. This work shows that the single-J model can be a good approach for the low-T spin dynamics of {Cr8Y8} and may have general significance for other weak ferromagnetic molecular rings. Determination of the Cr3+-Cr3+ exchange constant in {Cr8Y8} will benefit the study on the complicated magnetic interactions in chromium lanthanide complexes. The zero-field splitting which is suggested by HC data still calls for EPR or high-resolution INS technique to verify.
Similar content being viewed by others
Introduction
Magnetic molecules are promising candidates holding much potential in magnetic storage, spintronics, and quantum information processing1,2,3,4,5,6,7. Being neither simple paramagnets nor traditional bulk magnets, molecular magnets consist of a macroscopic number of identical uncorrelated magnetic clusters in the form of crystals with high quality. Each magnetic cluster is constructed from cooperatively-coupled paramagnetic metal ions, leading to novel macroscopic quantum behaviors such as quantum tunneling effect, etc8,9. Owing to the advances in inorganic chemistry, the structure of magnetic centers and the topology of exchange interactions in molecular magnets can be controlled at the synthesis level. By the cyclisation of short magnetic chains, molecular rings are forged and show remarkable spin dynamic properties at the crossover between classical and quantum regimes10,11,12,13,14. Such cyclic molecules provide finite model systems for 1D Heisenberg spin chains, as their periodic boundary conditions link their magnetic properties to those of infinite spin arrays.
One of the best characterized groups of cyclic molecules is the chromium rings family, e.g., the homometallic {Cr8}10,11,15,16, {Cr9}12 and {Cr10}17 rings, the heterometallic {Cr7M}18,19,20, {Cr8M}21,22,23, and {Cr9M}24 rings, and the bonded dimers {(Cr7Ni)2M}24,25, etc. Remarkable quantum properties such as quantum oscillations18 of total spins and quantum coherence26,27 have been observed. The deployment of chromium rings in quantum information applications has been explored and discussed6,26,27,28. As a crucial aspect for the understanding of the magnetic properties, the spin dynamics of chromium rings has been exclusively investigated by means of various experimental methods, such as magnetic property measurement, inelastic neutron scattering (INS), heat capacity (HC), nuclear magnetic resonance and electron paramagnetic resonance (EPR)10,11,12,16,17,18,19,20,21,22,29,30.
However, most of the magnetic molecular rings discovered so far are antiferromagnetic or ferrimagnetic. To the best of our knowledge, only a few ferromagnetic (FM) cyclic clusters have been reported to date and FM chromium rings are even rarer17,31,32,33. Recent research by us in the heterometallic 3d–4f rings {Cr8Ln8}34 (Ln = Gd, Dy, and Y) shows that a rich variety of magnetic properties is achievable by hosting different 4f ions. However, understanding to the mechanism of magnetic couplings in these large 3d–4f molecular rings is challenging due to the large Hilbert space and the complicated magnetic interactions. Besides the nearest-neighbor (NN) 3d–4f interactions, the next-nearest-neighbor (NNN) 3d–3d or 4f–4f interactions can be comparable to the NN interaction and thus play an important role in the determination of the ground state. It is difficult to determine the sign and the magnitude of the NNN interactions because this might cause over parameterization. Thus, the NNN interactions are generally ignored. To address this problem, diamagnetic substitution is a valuable approach, where insight into the 3d–3d (or 4f–4f) interactions can be achieved by substituting the magnetic 4f (or 3d) ions with nonmagnetic ones. But this approach has not been used often owing to the complexity in synthesizing the diamagnetic analogs.
By substituting magnetic Ln3+ ions with diamagnetic Y3+, we have isolated the largest Cr3+–Y3+ heterometallic molecular ring, [Cr8Y8(mdea)16(CH3COO)8(NO3)8]·3CH3CN (mdeaH2 = N-methyldiethanolamine), {Cr8Y8} for short, which is an isostructural diamagnetic analog of other reported {Cr8Ln8} complexes34. As a brief summary of its magnetic property, the χT product of 15.1 cm3 mol−1 K measured at 300 K is in accordance with the calculated value (15.0 cm3 mol−1 K) for eight Cr3+ spin-only ions with SCr = 3/2, gCr = 234. The Curie–Weiss fit to the χ−1 vs. T plot yields a positive Curie-Weiss temperature (Θ) of 2.19 K, indicative of weak FM coupling between Cr3+ moments in {Cr8Y8}. Since Y3+ is diamagnetic, the FM exchange interaction between Cr3+ NNs should be transmitted through a long –O–C–C–N–C–C–O– pathway justifying a weak coupling. {Cr8Y8} stands out in the {Cr8Ln8} family not only because it provides a rare example of FM chromium wheels, but more importantly because it allows a straightforward characterization of the Cr3+–Cr3+ magnetic interaction. The study on the complicated magnetic interactions in {Cr8Ln8} complexes can be greatly simplified with the knowledge of the Cr3+–Cr3+ magnetic interaction. In this paper, we exploit INS and HC methods to probe directly the low-lying energy states of {Cr8Y8} and quantitatively analyze the FM interaction between the Cr3+ moments.
Results
Heat capacity data
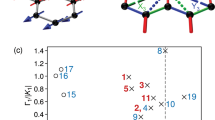
The HC of {Cr8Y8} was measured to get information on the low-lying energy levels. The temperature dependence of the molar specific heat C(T) at various external magnetic fields is plotted in Fig. 1. At fields below 0.5 T, the most striking features are two Schottky anomalies originating from the entropy change caused by the thermal population of low-lying discrete spin levels. As the field increases, the two Schottky anomalies shift towards higher temperature due to Zeeman effect and merge into one big hump at fields above 0.5 T. The significant dependence of C(T) on external magnetic fields indicates that the magnetic contribution dominates the total HC in this low-T region (T < 4 K), giving clear evidence of the existence of low-lying magnetic excitation.
Lacking a non-magnetic reference, the analysis of the HC data is restricted in the low-T range of 0.06–4 K, where the magnetic contribution dominates35,36. The lattice specific heat Clatt within this temperature range can be safely approximated to exhibit a cubic dependence on temperature, as given below37
where R is the gas constant, ΘD is the Debye temperature, rD = 408 is the number of atoms per {Cr8Y8} molecule. The magnetic specific heat Cmag is fitted with the Schottky model for a multi-level system, which can be expressed by37,38
where εi is the energy of spin level i. We define Δi as (εi – ε0), namely the energy gap between the energy level εi and the ground state ε0. The total specific heat is fitted with the sum of Eqs. (1) and (2). The solid lines in Fig. 1 represent the best fit to the data for 0, 0.1, 0.2, 0.5, 0.75, 1, 2, and 4 T. The dashed line stands for the fitted lattice contribution Clatt. The Debye temperature estimated from the fit is 170 ± 12 K, which cannot be determined precisely from the low-T HC only. Two energy gaps, Δ1 and Δ2, are considered and lead to a good fit to all specific heat data, although involving more energy gaps can result in a better fit. Below 0.2 K, the zero-field C(T) curve shows a sharp increase with decreasing T, which is assigned to the high-T tail of a Schottky anomaly. This Schottky anomaly corresponds to a very small energy gap of 0.009(9) meV and is tentatively attributed to the zero-field splitting (ZFS) of the S = 12 ground state of {Cr8Y8}. S is the total spin of a {Cr8Y8} molecule. The energy gaps resolved from the HC evaluation are summarized in Table 1.
Inelastic neutron scattering data
Time-of-flight INS technique provides direct information on low-lying magnetic states of molecular magnets by measuring the time of flight of scattered neutrons to determine their energy change during the scattering process39,40,41,42,43,44. The zero-field INS spectra of {Cr8Y8} were collected on the TOFTOF spectrometer at 0.5 and 20 K with a resolution of 10 μeV. Distinct excitations were observed on both the neutron-energy gain and loss sides. As expected for non-interacting magnetic molecules, the excitations are dispersionless. The neutron-energy loss (designated positive) spectra are shown in Fig. 2. The scattering intensity was obtained by integration over the scattering vector (Q) range between 0.27 and 0.45 Å−1. The INS intensity versus energy transfer spectra are best fitted with a Gaussian function to describe the strong central elastic line due to instrumental resolution and incoherent scattering, a quasielastic term (purple dash-dot line), a linear background (green dashed line), and a Gaussian term (blue dotted line) to describe the inelastic peak at 0.133(13) meV. The red solid line represents the total fit. The ZFS of Δ1 = 0.009 meV as obtained in HC data corresponds to a minor INS contribution denoted as INSZFS, which is very close to the strong elastic line and cannot be separated due to the limited instrumental resolution. Thus, in the fit of the TOFTOF spectra we fix the energy of INSZFS at 0.009 meV. We include INSZFS in the quasielastic term, which therefore consists of a minor Gaussian-shaped INSZFS and a Lorentzian function to account for the static disorder. The strong cold transition, denoted as INS2 in Fig. 2, is clearly observed at 0.133(13) meV, in good agreement with the energy gap Δ2 obtained from the evaluation of HC data. This cold transition can be attributed to the transition between the S = 12 ground state and the S = 11 excited state. In order to obtain reliable parameters of the quasielastic term, it is necessary to apply external magnetic field, given the fact that magnetic INS signal shall shift to higher energy transfer due to the Zeeman effect.
a, b Neutron-energy loss spectra of {Cr8Y8} measured on TOFTOF with an incident neutron wavelength of 10 Å at 0.5 and 20 K with inclusion of least-squares fits as red solid lines. A linear background (green dashed line) is assumed. The INS transition (blue dotted line) is described by a Gaussian function. The quasielastic term (purple dash-dot line) consists of a minor Gaussian function representing the INS contribution of zero-field splitting, and a Lorentzian function due to the static disorder. The error bars represent the standard deviation of the intensity.
We have investigated the response of INS spectra to the applied magnetic field from 0 to 4 T at 5 K on the NEAT spectrometer to achieve a comprehensive picture of the low-lying magnetic excitations of {Cr8Y8}. The integrated INS intensity vs. neutron-energy transfer plots for both the energy loss and the energy gain sides of the INS spectra collected at various fields are shown in Supplementary Fig. 1. Strong background intensity at low energy transfer range on the neutron-energy loss side can be observed and is difficult to be subtracted properly. Hence, we have taken only the neutron-energy gain spectra for further analysis, because the strong background intensity hinders the weak magnetic signal. The integrated INS intensities on the neutron-energy gain side are plotted in Fig. 3 as a function of neutron energy transfer. Employing similar fitting procedures for the TOFTOF data, we have analyzed the spectra collected on NEAT with varying magnetic fields. At 0 T, INS2 centers at 0.134(14) meV, consistent with the TOFTOF result. Another INS peak, denoted as INS1, is included in the fit to the data for nonzero external fields. INS1 originates from the Zeeman splitting of the S = 12 ground-state levels. As the field increases, both INS1 and INS2 shift to high neutron-energy transfer range owing to the Zeeman effect, justifying that they are magnetic in origin. In addition to this blue shift of neutron energy with increasing magnetic fields, we also observe the corresponding red shift as shown in Supplementary Fig. 1. The quasielastic component can be well separated from the inelastic magnetic signal at 4 T and thus be well fitted. Because the field dependence of this quasielastic component is subtle, it has been refined using the same values of parameters for all the spectra collected on NEAT. And again, the energy transfer for INSZFS is set as 0.009 meV because of the resolution limitation of NEAT. Note that the INS signal from ZFS is included in the quasielastic component (purple dash-dot line in Fig. 3) as in the fit to the TOFTOF data. Therefore, the magnetic INS peaks can be well extracted even for low fields, where they overlap with the quasielastic component. Both INS1 and INS2 are fitted with Gaussian functions. The total fitting results are shown in Fig. 3 as the red solid lines. The energy gaps obtained from INS transitions are summarized in Table 1.
a–f Neutron-energy gain INS spectra of {Cr8Y8} measured at 5 K on NEAT with an incident neutron wavelength of 8 Å and various magnetic fields from 0 to 4 T. Red solid lines are the best least-squares fits. A linear background (green dashed line) is assumed. The INS transitions (blue dotted lines) are described by Gaussian functions. The quasielastic contribution is shown as the purple dash-dot line. The error bars represent the standard deviation of the intensity.
Discussion
To understand the HC and INS results, it is necessary to explicitly consider the magnetic nature and the energies of the low-lying spin states. The Heisenberg spin Hamiltonian of {Cr8Y8} clusters can be given by the Eq. (3),
We propose a single-J model as an approach to the low-T spin dynamics of {Cr8Y8} to avoid over-parameterization. The single-J model we considered is shown in the inset of Fig. 4, where eight Cr3+ moments form a wheel-like structure and couple with NNs through a single FM exchange constant J. The calculation of energy multiplets has been carried out by using FIT-MART software package45 and the low-lying levels for the total cluster spin S = 12, 11, and 10 are plotted in Fig. 4. The energies of the spin levels are in units of |J|. The calculation yields an S = 12 ground state and two degenerate S = 11 excited states with a gap of ~0.879|J| above the ground state. This energy gap should correspond to the magnetic excitation marked as INS2 in Figs. 2 and 3. Since at 0 T the energy of INS2 is 0.133(13) meV, |J| is therefore determined to be 0.151(15) meV.
The single-J model is further examined by calculating the Zeeman splitting of the magnetic quantum states M for J = 0.151 meV and g = 2. As shown in Fig. 5, the black solid line represents the calculated splitting of the adjacent M levels of S = 12 ground state as a function of the magnetic field, while the red solid line is the calculated splitting between the lowest M levels of S = 12 ground state and S = 11 excited state. The green dashed line stands for the ZFS energy of 0.009 meV, which is negligible as compared to the energy gaps between the ground state and the excited state and the Zeeman splitting of the M levels for the investigated fields. Thus, the ZFS is not considered in the spin model and the calculation. The energies of INS1 and INS2 obtained from INS spectra are plotted as the squares in Fig. 5 as a function of the applied field, together with the energy gaps ∆1 and ∆2 determined from HC data. As shown in Fig. 5, the field dependence of INS1 and ∆1 agrees well with the Zeeman splitting of the adjacent M levels of the S = 12 ground state. Although the change of INS2 with fields is consistent with the Zeeman splitting between the S = 12 ground state and the S = 11 excited state, ∆2 shows large deviations at fields higher than 2 T. This suggests that it is inadequate to use only two energy gaps, ∆1 and ∆2, when fitting HC data. ∆1 and ∆2 can be considered as averaged energy gaps over the populated spin levels. More energy levels should be involved in the fitting procedure because for HC no selection rule needs to be followed. On the contrary, INS transitions are governed by the selection rules, ∆S = 0, ±1 and ∆M = 0, ±1. Hence in our case INS proves to be a rather unique tool for a direct characterization of the magnetic excitation, while HC serves as a complementary method for this purpose. The agreement of INS transitions with the calculation shows that the single-J model can be a good approach to the low-T spin dynamics of {Cr8Y8}. However, the HC of {Cr8Y8} suggests a ZFS of the ground state, which cannot be confirmed in our INS data due to the limited resolution. Before making possible adjustments to the single-J model, it will be necessary to validate the ZFS by means of EPR spectroscopy or high-energy-resolution INS methods (e.g., backscattering spectrometers) at lower temperatures (<1 K) using fully-deuterated samples.
The energy gaps obtained from INS and HC data are shown as the black squares and the blue circles, respectively. The Zeeman effect of the low-lying states is evaluated for the single-J model with J = 0.151 meV, as shown as the black and the red lines, which correspond to the splitting of the M levels of the S = 12 ground state and the energy gap between the M = − 12, S = 12 ground state and the M = − 11, S = 11 excited state, respectively. The green dashed line represents the zero-field splitting energy obtained from HC data. The error bars are obtained from the fit with 95% confidence intervals.
As reported in ref. 34, quantum Monte Carlo simulations reveal antiferromagnetic Cr3+–Gd3+ NN coupling constants with an average of 0.181 meV in {Cr8Gd8} without taking the ferromagnetic Cr3+–Cr3+ coupling into consideration. Since {Cr8Y8} and {Cr8Gd8} are isostructural, we presume that their Cr3+–Cr3+ coupling constants are very close. The comparable Cr3+–Gd3+ and Cr3+–Cr3+ coupling constants suggest that it is inadequate considering only the Cr3+–Gd3+ NN interactions for {Cr8Gd8}. The nature of the sign and magnitude of the complicated magnetic couplings in {Cr8Ln8} complexes certainly deserves a thorough investigation from both experimental and theoretical points of view. The study on the spin dynamics in {Cr8Y8} presented in this paper will serve as an important stepping stone of the way to achieve this goal. Further study on this issue is underway.
To summarize, the time-of-flight INS and HC measurements yield comprehensive magnetic spectra that provide the necessary benchmark for the low-lying magnetic excitations and thus the understanding to the low-T spin dynamics of {Cr8Y8} spin clusters. We have observed distinct features in both INS and HC spectra originating from magnetic excitations, which have been attributed to the low-lying spin levels of {Cr8Y8}. Despite the complexity of the system (complex structure, large matrix size, possible intercluster interaction and/or intracluster interaction beyond NNs), the low-T spin dynamics can be well described by the single-J model, where only the ferromagnetic exchange coupling between NN Cr3+ ions is considered. The exchange constant J is determined to be 0.151(15) meV. There is no evidence that {Cr8Y8} behaves like a single molecule magnet at temperatures down to 2 K34, possibly because the small zero-field splitting of the ground state and/or the small exchange interaction make the ground states difficult to be populated exclusively even at low temperatures of a few K. To this end, it would be interesting to synthesize {Cr8} rings with stronger ferromagnetic exchange coupling. Although the ZFS is yet to be confirmed by high-resolution techniques, the present INS data clearly reveal the low-T spin dynamics and support the single-J model as a reasonable approach, which may have general significance for the understanding to the spin dynamics of weak ferromagnetic rings. Knowledge of the Cr3+–Cr3+ magnetic coupling constant is crucial for the study on other {Cr8Ln8} complexes with more complicated magnetic interactions.
Methods
Sample description
The {Cr8Y8} crystals were synthesized by heating a mixture of Y(NO3)3·5H2O (365 mg, 1 mmol), Cr(acac)3 (349 mg, 1 mmol), N-methyldiethanolamine (357 mg, 3 mmol), triethylamine (303 mg, 3 mmol) and acetonitrile (8 mL) at 130 °C with autogenerous pressure for three days. Powder samples used in INS measurements were obtained by grinding polycrystal samples. Single-crystal x-ray diffraction shows that the sample crystalizes in orthorhombic space group Fddd. Please see ref. 34 for more details about the synthesis and the crystal structure characterization.
Heat capacity experiment
The field-dependent HC measurement was carried out on a Quantum Design physical property measurement system PPMS equipped with a liquid-helium cryostat and a 3He–4He dilution insert device. A small {Cr8Y8} crystal with a mass of 0.2 mg was used. The HC at constant pressure was determined with thermal relaxation technique46.
Inelastic neutron scattering experiment
INS experiment was done on two time-of-flight spectrometers, TOFTOF47 (Heinz Maier-Leibnitz Zentrum, Germany) and NEAT48 (Helmholtz Zentrum Berlin, Germany) with incident neutron wavelengths of 10 Å and 8 Å, respectively. About 3 g of non-deuterated powder sample was sealed under helium atmosphere in a hollow-cylinder copper container for both measurements. The background spectra were measured from the empty containers and subtracted during the data reduction. The detectors were calibrated by means of spectra from vanadium standards. We used an electromagnet to provide external magnetic fields up to 4 T on NEAT. The time-of-flight energy conversion and the data reduction were performed with the program Mantid49.
Data availability
All relevant data that support the findings of this study are available from the corresponding authors on request.
References
Bogani, L. & Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 7, 179–186 (2008).
Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 40, 3336–3355 (2011).
Affronte, M. Molecular nanomagnets for information technologies. J. Mater. Chem. 19, 1731–1737 (2009).
Candini, A. et al. Graphene spintronic devices with molecular nanomagnets. Nano Lett. 11, 2634–2639 (2011).
Leuenberger, M. N. & Loss, D. Quantum computing in molecular magnets. Nature 410, 789–793 (2001).
Troiani, F. et al. Molecular engineering of antiferromagnetic rings for quantum computation. Phys. Rev. Lett. 94, 207208 (2005).
Gatteschi, D., Caneschi, A., Pardi, L. & Sessoli, R. Large clusters of metal ions: the transition from molecular to bulk magnets. Science 265, 1054–1058 (1994).
Thomas, L. et al. Macroscopic quantum tunnelling of magnetization in a single crystal of nanomagnets. Nature 383, 145–147 (1996).
Gatteschi, D. & Sessoli, R. Quantum tunneling of magnetization and related phenomena in molecular materials. Angew. Chem. Int. Ed. 42, 268–297 (2003).
Baker, M. L. et al. Spin dynamics of molecular nanomagnets unravelled at atomic scale by four-dimensional inelastic neutron scattering. Nat. Phys. 8, 906–911 (2012).
Waldmann, O. et al. Elementary excitations in the cyclic molecular nanomagnet Cr8. Phys. Rev. Lett. 91, 237202 (2003).
Baker, M. L. et al. A classification of spin frustration in molecular magnets from a physical study of large odd-numbered-metal, odd electron rings. PNAS 109, 19113–19118 (2012).
Taft, K. L. et al. [Fe(OMe)2(O2CCH2Cl)]10, a molecular ferric wheel. J. Am. Chem. Soc. 116, 823–832 (1994).
Baniodeh, A. et al. High spin cycles: topping the spin record for a single molecule verging on quantum criticality. npj Quant. Mater. 3, 10 (2018).
Carretta, S. et al. Microscopic spin Hamiltonian of a Cr8 antiferromagnetic ring from inelastic neutron scattering. Phys. Rev. B 67, 094405 (2003).
van Slageren, J. et al. Magnetic anisotropy of the antiferromagnetic ring [Cr8F8Piv16]. Chem. Eur. J. 8, 277–285 (2002).
Low, D. M. et al. A family of ferro- and antiferromagnetically coupled decametallic chromium(III) wheels. Chem. Eur. J. 12, 1385–1396 (2006).
Carretta, S. et al. Quantum oscillations of the total spin in a heterometallic antiferromagnetic ring: evidence from neutron spectroscopy. Phys. Rev. Lett. 98, 167401 (2007).
Timco, G. A. et al. Heterometallic rings made from chromium stick together easily. Angew. Chem. Int. Ed. 47, 9681–9684 (2008).
Timco, G. A., McInnes, E. J. L. & Winpenny, R. E. P. Physical studies of heterometallic rings: an ideal system for studying magnetically-coupled systems. Chem. Soc. Rev. 42, 1796–1806 (2013).
Furukawa, Y. et al. Evidence of spin singlet ground state in the frustrated antiferromagnetic ring Cr8Ni. Phys. Rev. B 79, 134416 (2009).
Baker, M. L. et al. Inelastic neutron scattering studies on the odd-membered antiferromagnetic wheel Cr8Ni. Phys. Rev. B 86, 064405 (2012).
Baker, M. L. et al. Studies of a large odd-numbered odd-electron metal ring: inelastic neutron scattering and muon spin relaxation spectroscopy of Cr8Mn. Chem. Eur. J. 22, 1779–1788 (2016).
Affronte, M. et al. Molecular routes for spin cluster qubits. Dalton Trans. 23, 2810–2817 (2006).
Affronte, M. et al. Linking rings through diamines and clusters: exploring synthetic methods for making magnetic quantum gates. Angew. Chem. Int. Ed. 44, 6496–6500 (2005).
Ardavan, A. et al. Will spin-relaxation times in molecular magnets permit quantum information processing? Phys. Rev. Lett. 98, 057201 (2007).
Wedge, C. J. et al. Chemical engineering of molecular qubits. Phys. Rev. Lett. 108, 107204 (2012).
Ghirri, A. et al. Self-assembled monolayer of Cr7Ni molecular nanomagnets by sublimation. ACS Nano 5, 7090–7099 (2011).
Micotti, E. et al. Local spin moment distribution in antiferromagnetic molecular rings probed by NMR. Phys. Rev. Lett. 97, 267204 (2006).
Garlatti, E. et al. A detailed study of the magnetism of chiral {Cr7M} rings: an investigation into parametrization and transferability of parameters. J. Am. Chem. Soc. 136, 9763–9772 (2014).
Abbati, G. L. et al. A ferromagnetic ring of six manganese(III) ions with a S=12 ground state. Inorg. Chem. 37, 1430–1431 (1998).
Brechin, E. K. et al. Synthetic and magnetic studies of a dodecanuclear cobalt wheel. Chem. Commun. 17, 1860–1861 (2002).
Andres, H. et al. Studies of a nickel-based single-molecule magnet. Chem. Eur. J. 8, 4867–4876 (2002).
Qin, L. et al. Quantum Monte Carlo simulations and high-field magnetization studies of antiferromagnetic interactions in a giant hetero-spin ring. Angew. Chem. Int. Ed. 56, 16571–16574 (2017).
Fu, Z. et al. An approach to the magnetic ground state of the molecular magnet {Mo72Fe30}. N. J. Phys. 12, 083044 (2010).
Fu, Z. et al. Low-lying magnetic excitations and magnetocaloric effect of molecular magnet K6[V15As6O42(H2O)]·8H2O. EPL 112, 27003 (2015).
Evangelisti, M., Luis, F., de Jongh, L. J. & Affronte, M. Magnetothermal properties of molecule-based materials. J. Mater. Chem. 16, 2534–2549 (2006).
Tari, A. The Specific Heat of Matter at Low Temperatures. (Imperial College Press, London, 2003).
Basler, R. et al. Molecular spin clusters: new synthetic approaches and neutron scattering studies. ChemPhysChem 4, 910–926 (2003).
Furrer, A. & Waldmann, O. Magnetic cluster excitations. Rev. Mod. Phys. 85, 367–420 (2013).
Waldmann, O. Q dependence of the inelastic neutron scattering cross section for molecular spin clusters with high molecular symmetry. Phys. Rev. B 68, 174406 (2003).
Xue, Z.-L. et al. Neutron instruments for research in coordination chemistry. Eur. J. Inorg. Chem. 2019, 1065–1089 (2019).
Dunstan, M. A., Mole, R. A. & Boskovic, C. Inelastic neutron scattering of lanthanoid complexes and single-molecule magnets. Eur. J. Inorg. Chem. 2019, 1090–1105 (2019).
Moseley, D. H. et al. Inter-Kramers transitions and spin−phonon couplings in a lanthanide-based single-molecule magnet. Inorg. Chem. 59, 5218–5230 (2020).
Engelhardt, L., Garland, S., Rainey, C. & Freeman, R. FIT-MART: quantum magnetism with a gentle learning curve. Phys. Procedia 53, 39–43 (2014).
Hwang, J. S., Lin, K. J. & Tien, C. Measurement of heat capacity by fitting the whole temperature response of a heat-pulse calorimeter. Rev. Sci. Instrum. 68, 94 (1997).
Heinz Maier-Leibnitz, Z. et al. TOFTOF: cold neutron time-of-flight spectrometer. J. Large-scale Res. Facilities 1, A15 (2015).
Russina, M. et al. Upgrade project NEAT′2016 at Helmholtz Zentrum Berlin–What can be done on the medium power neutron source. Phys. B Condens. Matter 551, 506–511 (2018).
Arnold, O. et al. Mantid—data analysis and visualization package for neutron scattering and μSR experiments. Nucl. Instrum. Methods Phys. Res. Sect. A 764, 156–166 (2014).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11875325) and China Institute of Atomic Energy (Grant No. 16YZ201809).
Author information
Authors and Affiliations
Contributions
Z.F. and Y.Z. initiated and designed the project. L.Q. grew the crystals. K.S., Y.L. and D.C. supervised the project. Z.F., Y.X. and W.J. measured and analyzed HC data. Z.F., W.L., L.H., G.G. and M.R. collected and analyzed INS data on TOFTOF and NEAT spectrometers. All authors contributed to the interpretation of the data and the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fu, Z., Qin, L., Sun, K. et al. Low-temperature spin dynamics of ferromagnetic molecular ring {Cr8Y8}. npj Quantum Mater. 5, 32 (2020). https://doi.org/10.1038/s41535-020-0234-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0234-4