Resonant inelastic x-ray scattering study of vector chiral ordered kagome antiferromagnet

Abstract

We study the resonant inelastic x-ray scattering (RIXS) features of vector chiral ordered kagome antiferromagnets. Utilizing a group theoretical formalism that respects lattice site symmetry, we calculated the L-edge magnon contribution for the vesignieite compound BaCu₃V₂O₈(OH)₂. We show that polarization dependence of the L-edge RIXS spectrum can be used to track magnon branches. We predict a non-zero L-edge signal in the non-cross π−π polarization channel. At the K-edge, we derived the two-site effective RIXS and Raman scattering operator for two-magnon excitation in vesignieite using the Shastry–Shraiman formalism. Our derivation considers spin-orbit coupling effects in virtual hopping processes. We find vector chiral correlation (four-spin) contribution that is proportional to the RIXS spectrum. Our scattering operator formalism can be applied to a host of non-collinear non-coplanar magnetic materials at both the L and K-edge. We demonstrate that vector chiral correlations can be accessed by RIXS experiments.

Introduction

Chirality and magnetism can have an intimate relationship^1,2,3,4. In geometrically frustrated spin systems⁵, magnetic materials can harbor degenerate ground states⁶. The ordered magnetic phase on such a lattice can be characterized by a composite order parameter such as sublattice magnetization and vector chirality⁷. Vector spin chirality, which can act as an order parameter, is defined as κ_ij = S_i × S_j where S_i and S_j denote spins on lattice sites i and j. It signifies the rotational (clockwise or counterclockwise) sense of the non-collinear spin arrangement around a plaquette on the lattice. A vector chiral ordered state could induce the Dzyaloshinskii-Moriya (DM) interaction by the inverse DM mechanism^8,9,10. Thus, to have a deeper understanding of the fundamental physics of frustrated magnetic phases of matter, it is necessary to study and understand the tell-tale signatures of chirality³ and its associated chiral correlation functions. It is also worth noting that the chiral universality class has been proposed to characterize the nature of magnetic phase transition in a geometrically frustrated material¹¹. The recommended phase transition classification scheme is different from an unfrustrated magnet, which is known to be in the O(n) universality class.

DM interaction exists in magnetic bonds without inversion center¹². This favors a canted spin arrangement, which can give rise to the vector and the scalar chiral order. A vector chiral ordered phase, characterized by 〈κ_ij〉 ≠ 0, can exist in the chiral state. Moreover, the concept of scalar spin chirality χ_ijk = S_i ⋅ (S_j × S_k), where S_k is a spin, can be introduced to encompass the case of a non-coplanar spin arrangement. A non-coplanar arrangement is particularly important for our work that focuses on the q = 0 umbrella ordered state of a kagome lattice. In this magnetic pattern, the spins cant out of the kagome plane with an angle η. Such a q = 0 umbrella ordered state in the kagome lattice has been observed in jarosite KFe₃(OH)₆(SO₄)₂^7,13, vesignieite BaCu₃V₂O₈(OH)₂^14,15, Sr-vesignieite Cu₃SrV₂O₈(OH)₂^16,17, edwardsite Cd₂Cu₃(SO₄)₂(OH)₆.4H₂O¹⁸, and some variants of them. In Table 1, we list a collection of spin-1/2 copper-based kagome materials. Recently, kagome materials have attracted attention owing to correlation and topological effects also^19,20,21,22.

Table 1 Copper-based spin-1/2 kagome antiferromagnetic materials.

We consider the dynamical vector (scalar) chiral correlation, which is described by a four (six) -spin correlation function. Virtual hopping processes are the key to accessing the multi-spin correlation channel. It was suggested that the dynamical vector chirality response, ∫dte^iωt〈S_q(t) × S_−q(0)〉²³, which is a two-spin correlation function could be detected by polarized inelastic neutron scattering (INS)²⁴. But, this method is limited in its scope of applicability. The technique requires an unequal number of positive and negative vector chirality domains. This makes the approach invalid for a uniform vector chirality phase, such as in jarosite KFe₃(OH)₆(SO₄)₂. A theoretical proposal to study chirality has been made on the basis of the spin-charge-current effect^25,26, without any possible experimental realization, yet. In addition, multi-spin correlation functions are difficult to access unambiguously in an INS experiment^23,24. There have been several theoretical proposals to detect scalar chirality, too. These include Raman scattering^27,28, INS²⁹, and pre-edge resonant inelastic x-ray scattering (RIXS)³⁰. In all the above theoretical approaches, scalar spin chirality does not contribute to x-ray scattering intensity in the leading order. Thus, we focus on the dominant contribution arising from the vector chirality term.

In recent years, RIXS has rapidly developed as a useful experimental technique to probe correlated and frustrated states of matter^31,32,33. It has been successfully utilized to study electronic, magnetic, orbital, and lattice excitations^34,35,36,37. RIXS is a photon–in photon–out process, where the energy of the incoming photons are tuned to match the atomic absorption edge of specific elements in the material. Information on elementary excitations are measured by the differences between energy, momentum, and polarization of the incoming and outgoing photons. The dominant contribution of the RIXS spectra at the K-edge (corresponding to a 1s → 4p transition) of a Mott insulator originates from a four-spin correlation function³⁸. Thus, RIXS provides an opportunity to access vector chirality. Although, Raman scattering can be used to detect four-spin correlation, it has a very limited scope, being restricted to q ≈ 0.

It is known that DM interaction can induce long-range magnetic order in kagome antiferromagnets. There is a quantum critical point at D/J = 0.1, where J(D) is the exchange (out-of-plane DM) interaction strength in the Heisenberg model on a kagome lattice³⁹. When the in-plane DM interaction is also taken into account, there are two magnetic ordered phases with a q = 0 structure⁴⁰. The positive vector chiral phase where the spins cant out of the kagome plane is called the umbrella ordered state⁷. The other is the negative vector chiral phase where the spins are still coplanar. Later, in the discussion section we will put our results in the broader context of the classical phase diagram. Among the antiferromagnetically ordered insulating materials, the positive vector chiral ordered phase is observed more abundantly. However, there are very few negative chiral ordered phases. Two of them are CdCu₃(OH)₆(NO₃)₂.H₂O⁴¹ and YCu₃(OH)₆Cl₃⁴². The spectrum for the negative chiral phase is shown in Supplementary Fig. 8.

In this article, we develop a site symmetry respected theoretical formalism to compute the RIXS spectrum. The one-site effective scattering operator was constructed from group theoretical arguments. Our approach, valid for a wide range of realistic materials, was applied to the case of an umbrella ordered vector chiral kagome material vesignieite BaCu₃V₂O₈(OH)₂. We calculated the L and the K-edge magnon and two-magnon RIXS spectrum of vesignieite BaCu₃V₂O₈(OH)₂ arising out of the one- and two-site RIXS operator, respectively. Based on our calculations, we show that the L-edge RIXS polarization channels are sensitive to the magnon branches. Interestingly, we find a non-zero RIXS signal in the non-cross π−π polarization channel. The polarization dependence of the RIXS spectrum can be used to trace magnon branches. At the K-edge, we explicitly considered spin-orbit coupling in the Shastry–Shraiman formalism to derive the two-site effective RIXS-scattering operator for the two-magnon excitation. We found that a term proportional to vector spin chirality correlation can occur in the RIXS spectrum. Thus, in contrast to INS a four-spin vector chiral correlation function in the two-site contribution can be detected by RIXS. We also compare our results to Raman to showcase the relative advantage of RIXS. Based on our calculations, we propose that the vector chiral correlation functions can be accessed by current L and K-edge RIXS experiments (within current resolution limits).

Results

Model

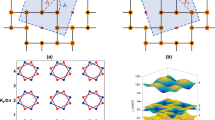
In an umbrella ordered state the spins cant out of the plane, which manifests as a weak out-of-plane ferromagnetic moment, see Fig. 1a. Broken mirror symmetry of the kagome plane⁴³, which is very common in these materials, see Fig. 1b, results in an in-plane DM interaction component D_p. Th umbrella ordering pattern is a consequence of the in-plane interaction. The ligand atoms surrounding the magnetic atom usually form a tilted crystal field. The presence of D_p, which breaks the rotational symmetry around the c -axis, is necessary to explain the spin wave gaps at the high-symmetry points⁴³. The degeneracy of positive and negative vector chirality in q = 0 type order is lifted by the out-of-plane DM interaction component D_z. The sign of D_z selects one of the chiral patterns. The phase diagram of J−D_z is symmetric for positive and negative chirality phase, but it is asymmetric once D_p is taken into account⁴⁰. In this article, we consider positive chirality that is common for a q = 0 type order in a kagome antiferromagnet such as jarosite and vesignieite.

Fig. 1: Kagome lattice with umbrella ordered spin arrangement.

The global kagome plane coordinate system (x⁰, y⁰, z⁰) and the crystal field coordinate system (x^c, y^c, z^c) are shown. The 2D kagome plane is set to x⁰−y⁰. Blue spheres denote copper atoms. Yellow and green spheres denote inequivalent oxygen atoms due to the compression of bond length along the local z axis. a Umbrella order where the spins align out of the kagome plane with a canting angle. b Sublattice indices are denoted by 1, 2, and 3. Out-of-plane component and the in-plane component of the DM interaction are indicated by the circles and the arrows on the bonds, respectively. The order of i and j in the DM interaction is clockwise in every triangular plaquette. c Crystal structure of β−vesignieite BaCu₃V₂O₈(OH)₂ created from atomic coordinate data⁵³.

We consider the following Heisenberg Hamiltonian

$$H={J}_{1}\sum _{\langle i,j\rangle }{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}+{J}_{2}\sum _{\langle \langle i,j\rangle \rangle }{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}+\sum _{\langle i,j\rangle }{{\bf{D}}}_{ij}\cdot \left({{\bf{S}}}_{i}\times {{\bf{S}}}_{j}\right),$$

(1)

on the kagome lattice. Here J₁ (J₂) denotes nearest-neighbor (next nearest-neighbor) antiferromagnetic super-exchange interaction, respectively. The DM interaction term D_ij can be written as D_ij = −D_p(n_i + n_j) + D_zz⁰, where ${{\bf{n}}}_{i}=\sin {\alpha }_{i}{{\bf{x}}}^{0}+\cos {\alpha }_{i}{{\bf{y}}}^{0}$, where (x⁰, y⁰, z⁰) is the global coordinate frame, see Fig. 1c. The sublattice dependent angles α_i are given by α₁ = 2π/3, α₂ = 0, and α₃ = 4π/3. The order of sites i and j in the DM term is specified in Fig. 1b, that is clockwise in every triangular plaquette. Our choice of the model is motivated by the fact that it is general enough to encompass a host of kagome materials^{43,44,45,46,47}, see Table 1. We solve this model using the approach outlined in Supplementary Note 1 and Supplementary Note 2 where we constructed the rotated linear spin wave Hamiltonian. In Supplementary Note 3 we perform the Bogoliubov diagonalization and supply the definition of the correlation function. In Supplementary Fig. 1 we show the spin ordering. In Supplementary Fig. 2 we show the actual crystal structure of vesignieite.

Vesignieite RIXS

The RIXS cross-section is computed using the Kramers–Heisenberg equation given by^34,38

$$\frac{{d}^{2}\sigma }{d\omega d\Omega }\propto \sum _{f}| {A}_{fi}{| }^{2}\delta (\omega -{\omega }_{fi}).$$

(2)

The transition amplitude

$${A}_{fi}=\left\langle f\left|{\hat{D}}_{out}\frac{1}{{\omega }_{in}-\hat{H}-i\Gamma }{\hat{D}}_{in}\right|i\right\rangle ,$$

(3)

contains the dipole transition operator ${\hat{D}}_{in}$ (${\hat{D}}_{out}$), which depend on the incoming (outgoing) momentum q_in (q_out) and the incoming (outgoing) photon polarization ε (${\varepsilon }^{\prime}$), respectively. The dynamics of the scattering operator ${\hat{D}}_{out}\frac{1}{{\omega }_{in}-\hat{H}-i\Gamma }{\hat{D}}_{in}$ is complicated. To consider core-hole effects in the intermediate state, the RIXS transition operator in the transition amplitude is typically replaced with an effective scattering operator. Thus, we have ${A}_{fi}=\langle f| {\hat{O}}_{{\boldsymbol{q}}}| i\rangle$, where q = q_in − q_out is the transfer momentum. The effective operator provides a tractable analytical approach, which captures the essential physics within a suitable approximation formalism. In this paper, we use group theory and the Shastry–Shraiman formalism²⁷ to compute the RIXS intensity. The derivation details are outlined in Supplementary Notes 4–8. We also observe that the energy scale of the chiral correlation is governed by exchange, but the intensity is governed by the DM interaction.

In general, the effective RIXS-scattering operator can be written as⁴⁸

$${\hat{O}}_{q}=\sum {e}^{i{\bf{q}}\cdot {{\bf{R}}}_{i}}({\hat{O}}_{i}+{\hat{O}}_{ij}+\cdots \ ),$$

(4)

where the summation is performed over site indices i, j,…, etc. The operators are classified according to the number of sites involved in the x-ray scattering process. These operators must be constructed to respect the local site symmetry, the lattice symmetry, and also reflect the core-hole effect to describe elementary excitations in different cases, such as magnon^36,49, two-magnon^38,50, orbiton⁴⁸, and spin-orbital excitation⁵¹. At zero temperature, the RIXS intensity is computed as

$$I({\bf{q}},\omega )=-\frac{1}{\pi }{\rm{Im}}{\int\nolimits_{-\infty }^{\infty }}dt\ {e}^{i\omega t}(-i)\langle T\ {\hat{O}}_{{\bf{q}}}^{\dagger }(t){\hat{O}}_{{\bf{q}}}(0)\rangle ,$$

(5)

where ${\hat{O}}_{{\bf{q}}}=\frac{1}{\sqrt{N}}{\sum }_{i}{e}^{i{\bf{q}}\cdot {{\bf{r}}}_{i}}{\hat{O}}_{i}$ and N is the total number of sites.

L-edge single spin excitation RIXS intensity

The one-site process is the main contribution at the L-edge, where the dominant virtual processes originate from photon-induced intrasite electron hops^30,34. As ${\hat{O}}_{i}$ is a local operator, it should be invariant under site symmetry operations^48,51,52. In general, for a (pseudo) spin system, which includes pure spins, an orbital system, and also spin-orbital coupled variables, the single-site operator ${\hat{O}}_{i}$ can be written as^36,48,51

$${\hat{O}}_{i}=\sum _{{\Gamma }_{n}}\sum _{j}{\alpha }_{i,{\Gamma }_{n},j}{P}_{i}^{{\Gamma }_{n},j}{T}_{i}^{{\Gamma }_{n},j}.$$

(6)

In the above, Γ_n denotes an irreducible representation, j denotes the component of group representation, and ${\alpha }_{i,{\Gamma }_{n},j}$ is a material-dependent coefficient, which carries the dipole transition information. ${P}_{i}^{{\Gamma }_{n},j}$ is the polarization factor. ${T}_{i}^{{\Gamma }_{n},j}$ is a combination of symmetry respected angular momentum operators. Both ${P}^{{\Gamma }_{n},j}$ and ${T}^{{\Gamma }_{n},j}$ form the basis for Γ_n representation.

The one-site operator is material dependent. Thus, we adopt a specific material to proceed further with our analysis. From Table 1, we choose vesignieite BaCu₃V₂O₈(OH)₂ whose copper atoms form a nearly perfect kagome lattice. The bond length difference between two inequivalent Cu²⁺ site is small^14,15. Moreover, it has been suggested that β−vesignieite BaCu₃V₂O₈(OH)₂ has a perfect kagome structure⁵³. In our calculations, we use the D_p and D_z parameters from ref. ¹⁴. of vesignieite and the atomic coordinate data of β−vesignieite from ref. ⁵³. Henceforth, we just call the compound vesignieite.

In vesignieite, the octahedron surrounding the Cu²⁺ ion is compressed along the local z axis of the crystal field. The octahedra tilt from the local z axis making an angle γ = 26^∘ with the kagome plane¹⁵. Atomic coordinate data from ref. ⁵³. suggests that the crystal field belongs to the D_4h point group. The hole occupies the ${d}_{{z}^{2}}$ orbital^14,15, which makes the compressed D_4h octahedral crystal field approximation self-consistent. Thus, using Eq. (6), we can write the RIXS-scattering operator ${\hat{O}}_{i}$ in the local D_4h site symmetry as

$$\begin{array}{lll}{\hat{O}}_{i}\,=\,{\alpha }_{{A}_{2u}}({\varepsilon }_{{x}^{c}}^{^{\prime} * }{\varepsilon }_{{y}^{c}}-{\varepsilon }_{{y}^{c}}^{^{\prime} * }{\varepsilon }_{{x}^{c}}){J}_{i,{z}^{c}}+{\alpha }_{{E}_{u},1}({\varepsilon }_{{z}^{c}}^{^{\prime} * }{\varepsilon }_{{x}^{c}}-{\varepsilon }_{{x}^{c}}^{^{\prime} * }{\varepsilon }_{{z}^{c}}){J}_{i,{y}^{c}}\\\qquad +\,{\alpha }_{{E}_{u},2}({\varepsilon }_{{y}^{c}}^{^{\prime} * }{\varepsilon }_{{z}^{c}}-{\varepsilon }_{{z}^{c}}^{^{\prime} * }{\varepsilon }_{{y}^{c}}){J}_{i,{x}^{c}},\end{array}$$

(7)

with terms linear in angular momentum operators. We ignore the constant terms as they do not contribute to the inelastic scattering. In the above expression ${\varepsilon }^{\prime}$ (ε) represents the outgoing (incoming) photon polarization variables. The superscript c implies an operator written in the crystal field coordinate system. It is possible to rewrite Eq. (7) as ${c}_{i}{({\varepsilon }^{^{\prime} * c}\times {\varepsilon }^{c})}_{i}{J}_{i}^{c}$, i denotes x, y, z. Hence, this operator vanishes when ${\varepsilon }^{^{\prime} * c}$ and ε^c are parallel to each other. For the material that we have considered, or other materials, in which spin-orbit coupling is small, we can replace J with S. Next, we calculate the transition matrix elements in the dipole approximation with the initial ${d}_{{z}^{2}}$ (hole) state wavefunction to determine the coefficients ${\alpha }_{{\Gamma }_{n},j}$. Based on the above considerations, the L₃-edge one-site operator is then given by

$$\begin{array}{lll}{\hat{O}}_{i}\,=\,\frac{4i}{3}({\varepsilon }_{{y}^{c}}^{^{\prime} * }{\varepsilon }_{{z}^{c}}-{\varepsilon }_{{z}^{c}}^{^{\prime} * }{\varepsilon }_{{y}^{c}}){S}_{i,{x}^{c}}+\frac{4i}{3}({\varepsilon }_{{x}^{c}}^{^{\prime} * }{\varepsilon }_{{z}^{c}}-{\varepsilon }_{{z}^{c}}^{^{\prime} * }{\varepsilon }_{{x}^{c}}){S}_{i,{y}^{c}}\\ \qquad-\frac{2i}{3}({\varepsilon }_{{x}^{c}}^{^{\prime} * }{\varepsilon }_{{y}^{c}}-{\varepsilon }_{{y}^{c}}^{^{\prime} * }{\varepsilon }_{{x}^{c}}){S}_{i,{z}^{c}}.\end{array}$$

(8)

It is vital to note that the effective one-site RIXS-scattering operator was constructed purely based on local site symmetry. The geometry of the lattice and the magnetic order was not important in constructing it. This implies that this operator can be applied to study other materials with the same local symmetry and different magnetic phases.

The linear photon polarization σ(π) is perpendicular (parallel) to the scattering plane for the RIXS experimental geometry setup, see Supplementary Fig. 3. The polarization and transferred momentum can be tuned by varying the angle of incidence. We set the scattering angle between the incoming photon and outgoing photon to 130^∘. For vesignieite, it can be shown that the entire first Brillouin zone can be comprehensively covered in a RIXS experiment using our proposed experimental setup as outlined in the Supplementary Note 4.

In Fig. 2, we show the one-site contribution results at the L₃-edge. As the σ polarization is perpendicular to the scattering plane, we can infer from Eq. (8) that the contribution from the σ_in–σ_out channel is zero. The π_in –π_out description is in the next paragraph. In the total dynamical structure factor (DSF) plot, Fig. 2a, the middle (blue) band in the inset of Fig. 2a and the highest (red) band almost merge together when ω > 0.8J₁S. However, it should be noted that these three bands do not actually touch each other. A detailed close up view of the dispersions, along with descriptions is provided in Supplementary Figs. 4 through 7. Furthermore, the spectral weight is small around the Γ point. These features make it hard to extract the complete dispersion from INS¹³. From the L₃-edge RIXS spectra with different polarization combination, Fig. 2b–d, it is clear that the x-ray polarization channels are sensitive to a varying degree. The σ_in –π_out channel is most sensitive to the middle (blue) band with a very small spectral weight for the lowest (green) band. However, the spectral weight in the green band is enhanced in the π_in–σ_out channel, and the π_in−π_out channel mainly detects the red band. We also compute the DSF using parameters for vesignieite¹⁴ to compare to our L-edge spectrum using D_p/J₁ = 0.19, D_z/J₁ = 0.07, and J₂ = 0. We define the DSF as ${\sum }_{\alpha ,\beta }({\delta }_{\alpha \beta }-{\hat{q}}_{\alpha }{\hat{q}}_{\beta }){S}^{\alpha \beta }({\bf{q}},\omega )$, where ${S}^{\alpha \beta }({\bf{q}},\omega )=\mathop{\int}\nolimits_{-\infty }^{\infty }\frac{dt}{2\pi }\langle {S}_{q}^{\alpha }(t){S}_{-q}^{\beta }(0)\rangle {e}^{i\omega t}$ and α, β refers to x, y, and z. The unit vector component in the direction of q is denoted by $\hat{q}$. To be consistent with INS we have projected out the longitudinal momentum component.

Fig. 2: Magnon excitation in S = 1/2 kagome vesignieite BaCu₃V₂O₈(OH)₂.

a Inelastic neutron scattering (INS) spectrum. Magnon dispersion is shown in the inset. b–c show in-out polarization dependence of one-site Cu L₃ edge resonant inelastic x-ray scattering spectrum. b σ_in−π_out polarization. c π_in−σ_out polarization. d π_in−π_out polarization. ω represents energy transfer in meV. J₁ represents nearest-neighbor exchange energy in meV.

The three magnon branches in a kagome antiferromagnet have a real space interpretation. There is one in-plane mode and two out-of-plane modes^43,44,54. The nearly flat band is one of the out-of-plane modes. Naively, from the perspective of angular momentum conservation, one may infer that in a specific polarization combination the photon will primarily couple to a rotation mode of the magnon. In Fig. 2, the σ_in−π_out channel couples to the in-plane magnon mode (blue branch), the π_in−σ_out couples both to the out-of-plane magnon mode (green branch) and to the in-plane magnon mode (blue branch). The π_in−π_out couples to the other out-of-plane mode (red branch). So the specific polarization combinations do selectively couple to specific rotation modes in the positive vector chiral phase. But, as explained in the Supplementary Note 5, it does not follow a solitary dispersion. Analysis of the negative chiral phase that exists in a coplanar state suggests that the polarization dependence does depend on the vector chiral ordering.

A non-zero RIXS intensity signal is expected in the cross polarization channels σ_in−π_out or π_in−σ_out. However, the appearance of a non-zero L-edge signal in the non-cross polarization channel π_in –π_out is counterintuitive^36,49. In general, the one-site RIXS operator has the form ${c}_{i}{({\varepsilon }^{^{\prime} * c}\times {\varepsilon }^{c})}_{i}{S}_{i}^{c}$. Owing to local site symmetry, the operators are defined in the local crystal coordinate system. The coefficients c_i are restricted by the selection rule of the dipole transition. In the case of a hole in a ${d}_{{x}^{2}-{y}^{2}}$ orbital (as in a cuprate), using selection rules, only the S^z component survives in the RIXS operator. However, for a hole in the ${d}_{{z}^{2}}$ orbital (as in a vesignieite) all the spin components S_x, S_y, S_z are allowed. In fact, we can show that for the Γ–K path considered in our case with ϕ = 0, the coefficient of S_x in the one-site RIXS operator after rotation becomes $-2(\cos 2\beta \sin \alpha +\cos \alpha \sin 2\beta \sin \gamma )\sin \varphi$. So, the spin-flip intensity is non-zero in this case.

In high-symmetry crystals such as a cuprate, the local crystal coordinate system is aligned with the global lattice frame. Thus, when considering a RIXS signal in the π_in−π_out channel, ${\varepsilon }^{^{\prime} * c}\times {\varepsilon }^{c}$ gives only the x−y component. Furthermore, based on selection rule analysis we have c_x = c_y = 0, as the hole is in the ${d}_{{x}^{2}-{y}^{2}}$ orbital. Thus, the scattering operator does not give rise to spin-flip terms. But if the hole is in a ${d}_{{z}^{2}}$ orbital (as in our compound) the c_x and c_y coefficients are non-zero and the spin-flip intensity can be non-zero in general. In addition, for vesignieite that has a lower crystal symmetry than a cuprate, the π polarization can be decomposed into σ^c and π^c components in the local crystal coordinate system. This lower symmetry makes it possible to have a non-zero spin-flip intensity in the π_in–π_out channel. Our theoretical finding of a non-zero signal in the non-cross polarization channel has been recently experimentally observed in thin films of NBCO by Fumagalli et al.⁵⁵.

K-edge two-magnon RIXS intensity

The two-site term in Eq. (4) is the leading contribution at the Cu K-edge RIXS, as spin-orbital coupling is absent for 1s electrons. Thus, a one-site single spin-flip excitation is forbidden in this case. We use the dipole transition operator in D_4h crystal field symmetry given by ${\hat{D}}_{in}={\varepsilon }_{x}{p}_{x}^{\dagger }s+{\varepsilon }_{y}{p}_{y}^{\dagger }s$ in the Kramers–Heisenberg amplitude Eq. (3). The most important feature of the intermediate state core hole is the modification of the super-exchange process^38,50,56. Hence, it is necessary to carefully consider for a Mott insulator how the virtual hopping processes are modified by the core hole. Thus, we use the Shastry–Shraiman formalism ^27,30.

We can generalize the RIXS formalism to include material intrinsic spin-orbit coupling effect at the K-edge during the virtual hopping process. The full intermediate state Hamiltonian is given by $\hat{H}={\hat{H}}_{t}+{\hat{H}}_{U}+{\hat{H}}_{pho}$, where ${\hat{H}}_{t}$ is the electron hopping part, ${\hat{H}}_{U}$ is the Hubbard interaction, and ${\hat{H}}_{pho}$ is the pure photon part^57,58. The presence of spin-orbital coupling introduces a non-abelian phase in the hopping amplitude. Thus, we have ${\hat{H}}_{t}={\sum }_{i,j,\sigma }{b}_{ij}{c}_{i\sigma }^{\dagger }{c}_{j\sigma }+{\sum }_{i,j,\sigma ,\sigma ^{\prime} }{c}_{i\sigma }^{\dagger }{[{{\boldsymbol{C}}}_{ij}\cdot {\boldsymbol{\sigma }}]}_{\sigma \sigma ^{\prime} }{c}_{j\sigma ^{\prime} }$, where σ is the Pauli matrix vector. C_ij is purely imaginary since spin-orbital coupling is time reversal invariant. We set C_ij = in_ij∣C_ij∣, where n_ij is a unit vector related to spin-orbit coupling. The hopping part can then be recasted as ${\hat{H}}_{t}={\sum }_{ij}{t}_{ij}{{\boldsymbol{c}}}_{i}^{\dagger }{A}_{ij}{{\boldsymbol{c}}}_{j}$, where ${{\boldsymbol{c}}}_{j}={({c}_{j\uparrow },{c}_{j,\downarrow })}^{T}$ with ${t}_{ij}\cos {\theta }_{ij}={b}_{ij}$, ${t}_{ij}\sin {\theta }_{ij}=| {C}_{ij}|$, and ${A}_{ij}={e}^{i{\theta }_{ij}{{\boldsymbol{n}}}_{ij}\cdot {\boldsymbol{\sigma }}}$ (a 2 × 2 matrix). As we are considering a Mott insulator case where t ≪ U, we can regard H_t as a perturbation^27,30. Thus, the leading inelastic x-ray scattering term can be written as

$${\hat{O}}_{{\boldsymbol{q}}}={\eta }_{c}\sum _{i,j}{e}^{i{\boldsymbol{q}}\cdot {{\boldsymbol{r}}}_{i}}\left[{J}_{ij}{{\boldsymbol{S}}}_{i}\cdot {{\boldsymbol{S}}}_{j}+{{\boldsymbol{D}}}_{ij}\cdot ({{\boldsymbol{S}}}_{i}\times {{\boldsymbol{S}}}_{j})\right],$$

(9)

with the polarization factor ${\varepsilon }_{x}^{^{\prime} * }{\varepsilon }_{x}+{\varepsilon }_{y}^{^{\prime} * }{\varepsilon }_{y}^{^{\prime} * }$, which is an overall multiplicative factor to the RIXS operator. The exchange and DM interaction modification factor η_c is a function of the core-hole potential U_c and U. We used Eq. (9) to calculate the results in Fig. 3. Note, we outline the transformation to the local moment coordinate system in Supplementary Note 6.

Fig. 3: Two-site RIXS spectra in vesignieite.

The total spectrum consist of the exchange I^J part, the Dzyaloshinskii-Moriya I^D part, which is proportional to vector chiral correlation, and the mixed I^m part. a I^J, b I^D, c the total spectrum I = I^D + I^D, and d the two-magnon density of states, D(q, ω).

For a comprehensive understanding, we also show the ultrashort core-hole lifetime (UCL) approximation derivation^38,50 of the RIXS operator Eq. (9) in Supplementary Note 7. In general, for a Mott insulator the condition H_t ≪ ω_in − H_U − H_pho − iΓ needs to be obeyed. Thus, the Shastry–Shraiman formalism, which is based on the above condition, is a more natural expansion scheme compared with UCL. The UCL approximation is a sufficient but not necessary condition. The Shastry–Shraiman approach is the more general scheme. Note, in our formalism, the one-site RIXS operator corresponds to the n = 0 term³⁰. The group theory inspired one-site RIXS operator construction is general enough to allow higher order terms beyond the linear spin operator dipole transition level. But, due to practical calculation reasons, the Shastry–Shraiman formalism is restricted to the dipole approximation implicitly. It is challenging to calculate a multipole contribution in the Shastry–Shraiman formalism.

The kagome lattice belongs to the D_3d point group. Thus, an effective two-site scattering operator Eq. (9) corresponds to the A_1g irreducible representation. Using the Shastry–Shraiman formalism, we can derive the Raman scattering operator (which corresponds to a two-site term) expression as

$${\hat{O}}_{{\rm{Raman}}}\propto \sum _{ij}\frac{({{\boldsymbol{\epsilon }}}^{^{\prime} * }\cdot {\boldsymbol{\delta }})({\boldsymbol{\epsilon }}\cdot {\boldsymbol{\delta }})}{{\omega }_{i}-U}\left[{J}_{ij}{{\boldsymbol{S}}}_{i}\cdot {{\boldsymbol{S}}}_{j}+{{\boldsymbol{D}}}_{ij}\cdot ({{\boldsymbol{S}}}_{i}\times {{\boldsymbol{S}}}_{j})\right],$$

(10)

which has three channels A_1g, (E_g, 1), and (E_g, 2). The contribution to the elastic channel comes from A_1g. In Supplementary Note 8 we provide the details of this derivation.

Both the RIXS and the Raman processes measure a four-spin correlation function. Whereas Raman is restricted mainly to q ≈ 0, RIXS has the ability to comprehensively explore the Brillouin zone for all energy scales (resolution and scattering geometry permitting). The two-site RIXS intensity can be divided into three parts. First, the exchange part I^J is ~ 〈(JS_k ⋅ S_l), (JS_i ⋅ S_j)〉. The second chiral DM part I^D contribution is ~ 〈D ⋅ (S_k × S_l), D ⋅ (S_i × S_j)〉. Finally, we have a mixed contribution I^m coming from the overlap of the exchange and the chiral DM part. The chiral contribution measures the projection of the vector chirality correlation function, which is currently inaccessible via a direct measurement^23,24. Moreover, in the umbrella ordered state, the scalar chirality is proportional to vector chirality²⁶ since 〈S_i ⋅ (S_j × S_k)〉 ≈ 〈S_i〉 ⋅ 〈S_j × S_k〉. Thus, the I^D part carries information related to the six-spin scalar chiral correlation function.

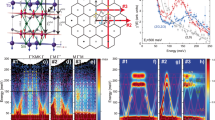
The two-site RIXS intensity is shown in Fig. 3. It can be proved that all physically meaningful RIXS intensities are non-negative (see Supplementary Note 6). The mixed part is real but with both positive and negative intensity contribution. According to the definition of RIXS intensity Eq. (5), only the correlation functions, which have the form $\langle T\hat{b}(t)\hat{b}(t){\hat{b}}^{\dagger }(0){\hat{b}}^{\dagger }(0)\rangle$ contribute at zero temperature, where $\hat{b}$ is the Bogoliubov quasiparticle operator. This implies, we only require the ${\hat{b}}^{\dagger }{\hat{b}}^{\dagger }$ terms in ${\hat{O}}_{{\bf{q}}}$. Thus, at the Γ point where q = 0, the two-site operator Eq. (9) reduces to the Hamiltonian. As Bogoliubov transformation eliminates the $\hat{b}\hat{b}$ and ${\hat{b}}^{\dagger }{\hat{b}}^{\dagger }$ terms in the Hamiltonian, the two-site intensity is identically zero at q = 0, see Fig. 3(c). This argument provides a simple proof for an exact zero intensity signal at the Γ point for a two-site contribution. Our argument is valid in other cases also^50,59,60. Thus, at this point the intensity I^J + I^D = −I^m. Although the RIXS intensity is zero at the Γ point, information on the two-magnon excitation at zero wave vector can be extracted from two-magnon Raman scattering. Here, as we calculate the non-interacting case, the spectra of the two-site contribution has the same shape as the two-magnon density of states D(q, ω) = ∑_k,m,nM δ(ω−ω_m,k−ω_n,q-k).

Discussion

Our calculations suggest that the cross-section at the L-edge RIXS is not simply proportional to DSF^35,61. It is obvious that the spectral weight distribution in DSF and in RIXS are different in Fig. 2. The spin operator in the effective one-site RIXS operator Eq. (8) is determined from the local symmetry. This implies that in the local crystal field coordinate system such spin operators can have x or y components. So, the single magnon can be detected in Cu L-edge RIXS^36,49. After rotation of the spin operator and the polarization, the effective operator can be written as ${\hat{O}}_{i}=A({\bf{q}},{\alpha }_{i}){S}_{i,x}+B({\bf{q}},{\alpha }_{i}){S}_{i,y}+C({\bf{q}},{\alpha }_{i}){S}_{i,z}$ with momentum-dependent coefficients A, B, and C. These relationships are too complicated to be listed in the main text. We describe the procedure to obtain them in Supplementary Note 4.

In the magnetic ordered phase, the leading RIXS contribution is I_RIXS ~ ∑_nM(q)δ(ω − ω_nq) where n is the band index, ω_nq is the magnon dispersion, and M(q) is the RIXS matrix element. So, the overall shape of the spectrum are along the dispersion. In a tetragonal system with a collinear magnetic order such as a cuprate, the local z axis of the crystal field coincides with the global z axis. The spins lie in the x−y plane. So, the rotation of the spin operator in the effective one-site RIXS operator is the same as in DSF³⁶. Thus, RIXS can have very similar spectral weight as in DSF^36,49. But in the kagome material with a non-collinear magnetic order studied here, these rotations make RIXS totally different from DSF. L-edge RIXS relies on spin-orbit coupling of the core states that makes RIXS different from DSF. One can consider magnon–magnon interaction which is known to have significant renormalization effect on the frustrated kagome antiferromagnet⁴⁴. In this case, one can replace the free magnon propagator by the renormalized one in Eq. (5) to consider this effect. This modification and considering any potential magnon decay effects will not change the main conclusions of this article, however.

We discuss the vector chiral RIXS correlation contribution I^D. We derived Eq. (9) by considering virtual hopping in the core-hole modified super-exchange process. The antisymmetric exchange term is always allowed by symmetry in the lattice without bond inversion center. So, it is natural to include this term in the general kagome material, even with weak spin-orbital coupling. For other lattice configurations, such as the triangular lattice, the honeycomb lattice, and even the square lattice, this antisymmetric exchange can exist for some materials. The polarization sensitivity is introduced in the photon absorbing and emitting process at the core-hole site. Hence, the exchange and the DM term has the same polarization dependence factor.

The degeneracy of the positive and negative vector chiral state is lifted by DM interaction, which is intrinsic to the material. Here, we discuss the difference between the spectrum of the positive and the negative vector chiral state. In Fig. 4a, we show our computed classical phase diagram of the J₁−D_z−D_p model⁴⁰. The negative vector chiral phase is always coplanar. But, the positive vector chiral phase is coplanar only when D_p = 0. Since there are very few insulating negative vector chiral kagome materials^41,42 and parameters are unavailable (presently), we choose D_p = 0.19J₁ and D_z = −0.07J₁ for the negative vector chiral vesignieite. These two parameter sets are denoted by the black points in the Fig. 4a. The INS spectrum, the two-site RIXS intensity, and two-magnon density of state of this negative vector chiral phase are shown in Fig. 4b–d. In contrast to positive chiral materials (Fig. 2a), the spin wave dispersion of this phase is gapless. So when D_p ≠ 0, which is a common feature in broken mirror symmetry kagome planes, the negative vector chiral phase is gapless. When D_p = 0, both chiral phase are coplanar (η = 0) and gapless, they correspond to ±D_z. We can identify the difference between the positive and the negative vector chiral state using $\sin ({\alpha }_{i}-{\alpha }_{j})$ (even though at the linear spin wave level this distinction is not apparent).

Fig. 4: Phase diagram and resonant inelastic x-ray scattering response of negative vector chiral phase.

a Classical phase diagram. The blue (red) region indicates the positive (negative) vector chiral phases. The spins in the positive vector chiral phase cant out of the kagome plane when D_p ≠ 0. The red dashed line represents coplanar positive vector chiral phase with D_p = 0. The spins in the negative vector chiral phase is coplanar. The parameters of the black points are D_p = 0.19J₁ and D_z = ±0.07J₁. Vesignieite is the point with positive D_z. b INS spectrum. Magnon dispersion is shown in the inset, c two-site RIXS spectrum, and d two-magnon density of state of the negative vector chiral phase with D_p = 0.19J₁, D_z = −0.07J₁.

The exchange and chiral part of our RIXS contribution could potentially be separated experimentally. Here, we consider two proposals to study vector chiral correlation in RIXS. Chiral correlation can have higher critical temperature than the spin correlation^11,62,63,64. Thus, chiral correlations could be studied around the magnetic critical ordering temperature where spin correlation is suppressed, but chiral correlation survives. Another proposal is based on the spin current interpretation of vector chirality^8,25,26. It has been pointed out that electric polarization is proportional to vector chirality. Thus, vector chirality can be tuned by an external electric field.

Our predicted RIXS intensity features can be verified experimentally within the current state-of-the-art RIXS resolution, which is of the same order of magnitude^3,65. For example, consider the magnetically ordered kagome materials outlined in Table 1, and jarosite^13,46, which have J~5 meV. Thus, the one-site RIXS spectrum has an energy of the order of ~2J₁S~10 S meV, see Fig. 2. This energy is ~5 meV for a S = 1/2 material and 25 meV for S = 5/2 material. In the magnetic ordered phase, the vector chiral correlation is a two-magnon (four-spin) correlation function. So, the two-site RIXS spectrum is ~3J₁S~15 S meV. Thus, the energy is ~7.5 meV for S = 1/2 and 37.5 meV for S = 5/2. We hope these resolution estimates and the results in our current paper will encourage RIXS experimentalists to study the kagome materials family.

In this article, we studied the L- and K-edge RIXS features of an umbrella ordered kagome antiferromagnet. Considering the one- and two-site RIXS contribution we have evaluated the magnon and two-magnon contributions, respectively. We have used a general site symmetry respected method to construct the one-site effective RIXS operator, which can be used to study spin, orbital, and spin-orbital excitations. We revealed that the one-site contribution in the L-edge RIXS can be entirely different from the DSF. Considering vesignieite as an example, we showed that the magnon dispersion of vesignieite has a non-zero L-edge RIXS intensity in the non-cross polarization channel of incoming and outgoing x-ray photons. We also derived the two-site effective RIXS operator at the K-edge in the presence of DM interaction (considering spin-orbit interaction). Utilizing a Shastry–Shraiman formalism that incorporates spin-orbit coupling, we calculated the vector chiral correlation contributions at K-edge RIXS. We compare and contrast our RIXS findings with those of INS and Raman. We provide two proposals to separate the vector chiral correlation in the total RIXS spectrum. Finally, we note that our RIXS operator construction formalism should apply to non-coplanar non-collinear magnetic ordering on lattices beyond the kagome case ⁶⁶.

Methods

Linear spin wave theory

We use spin wave theory to study the dynamical vector chirality of the magnetically ordered q = 0 phase of antiferromagnetic kagome materials. To carry out the calculation, it is necessary to express the spin operators in the local moment coordinate system as

$$\begin{array}{lll}{S}_{i,{x}^{0}}\,=\,{S}_{i,x}\cos {\alpha }_{i}+{S}_{i,y}\sin {\alpha }_{i}\sin \eta +{S}_{i,z}\sin {\alpha }_{i}\cos \eta ,\\ {S}_{i,{y}^{0}}\,=\,-{S}_{i,x}\sin {\alpha }_{i}+{S}_{i,y}\cos {\alpha }_{i}\sin \eta +{S}_{i,z}\cos {\alpha }_{i}\cos \eta ,\\ {S}_{i,{z}^{0}}\,=\,-{S}_{i,y}\cos \eta +{S}_{i,z}\sin \eta ,\end{array}$$

(11)

where α_i are sublattice dependent angles α₁ = 2π/3, α₂ = 0, and α₃ = 4π/3 for the three sublattices respectively, see Fig. 1; α₁ = 4π/3, α₂ = 0, and α₃ = 2π/3 for the negative vector chiral phase, see Fig. 4a. The canting angle is η, where η = 0 corresponds to spins in the kagome basal plane. Next, we perform Holstein-Primakoff transformations at the linear spin wave level using ${S}_{i,z}=S-{a}_{i}^{\dagger }{a}_{i},\ {S}_{i}^{-}\approx \sqrt{2S}{a}_{i}^{\dagger },\ {S}_{i}^{+}\approx \sqrt{2S}{a}_{i}$. The Fourier transformed spin wave Hamiltonian can be obtained using the transformation ${a}_{\alpha ,l}=\frac{1}{\sqrt{N}}{\sum }_{{\bf{k}}}{a}_{\alpha ,{\bf{k}}}{e}^{i{\bf{k}}\cdot ({{\bf{R}}}_{l}+{{\boldsymbol{\rho }}}_{a})}$, where ρ_a is the displacement of the α atom in the l-th unit cell. N represents the total number of unit cells (the details of the spin wave Hamiltonian is given in the Supplementary Note 1 and Supplementary Note 2). It should be noted that there is no analytical solution even at the linear spin wave level when the canting angle η ≠ 0. Thus, we have performed a numerical Bogoliubov diagonalization transformation of the Hamiltonian. A comprehensive and detailed procedure for diagonalizing the quadratic Hamiltonian is given in the Supplementary Note 3.

RIXS and Raman operator derivation

RIXS and Raman are both photon–in photon–out process. The transition amplitude A_fi can be written as

$${A}_{fi}=\left\langle f\left|{\hat{H}}_{coup}\frac{1}{{\omega }_{in}-\hat{H}-i\eta }{\hat{H}}_{coup}\right|i\right\rangle ,$$

(12)

where ${\hat{H}}_{coup}$ is the light-matter coupling Hamiltonian. In RIXS, the incoming beam is tuned to match the absorption edge of the specific elements to cause the 1s → 4p transition. In this case, ${\hat{H}}_{coup}$ can be simplified to a dipole transition operator $\hat{D}$. In Raman, the incoming beam is visible light with several eV energy and close to the Hubbard gap. Thus, ${\hat{H}}_{coup}$ describes the intersite electron hops coupled to the electromagnetic field of photon. This can be introduced by a Peierls substitution ${\hat{H}}_{coup}={\sum }_{ij}{t}_{ij}{e}^{i\frac{e}{\hslash c}\mathop{\int}\nolimits_{j}^{i}{\boldsymbol{A}}({\boldsymbol{r}})\cdot d{\boldsymbol{l}}}{{\boldsymbol{c}}}_{i}^{\dagger }{A}_{ij}{{\boldsymbol{c}}}_{j}$. Once ${\hat{H}}_{coup}$ is determined, the transition amplitude (or the effective scattering operator) can be calculated using perturbation expansion. The electron hopping part in the Hamiltonian $\hat{H}$ is regarded as a perturbation in the Shastry–Shraiman formalism²⁷. Then, the intermediate state propagator ${({\omega }_{in}-\hat{H}-i\eta )}^{-1}$ can be expanded as stated in the main text. We are interested in the low-energy excitations of our model. So, we insert a complete set of wave functions of one hole and one double occupied state. Then the electron operator c and c^† can be represented by spin operators and we find the spin Hamiltonian. Full details of the calculation is supplied in Supplementary Note 4 through Supplementary Note 8.