Introduction

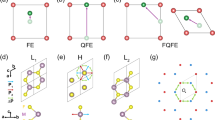
Ferrielectricity, the equivalent of ferrimagnetism, can be termed as antiferroelectric order but with a switchable polarization, as sketched in Fig. 1a. The first proposed ferrielectric system was a composition of two antiferroelectric compounds NaVO3 and NaNbO31, but subsequent experiments did not support this claim2. Despite a long history, the existence of ferrielectricity in solid crystals remains rare, except in liquid crystals3. Recently, some solids were claimed to be ferrielectric. For example, in the layered-structure CuInP2S6, the positions of Cu and In are always opposite within each unit cell (u.c.), which can be recognized as two uncompensated polar sub-lattices with antiparallel alignment4,5. In geometric ferroelectrics, such as Ca3Ti2O7 and some perovskite superlattices, the displacements of ions are opposite between layers, which can also been recognized as two uncompensated dipole moments6,7. Despite the macroscopic and phenomenological analogy as shown in Fig. 1a, it should be noted that there is a key difference between the ferrimagnetic and ferrielectric systems in the microscopic level. Different from the spin moment which can be defined on a single ion, the definition of a charge dipole involves more than one ion and thus may have multiple choices in ionic crystals. By choosing different ions as a dipole unit, multiple dipole values for a sub-lattice can be obtained8. In this sense, the Cu-In pair in CuInP2S6 or bilayer in Ca3Ti2O7 can be treated as a dipole unit, which are indeed entangled simultaneously4,6. Therefore, these systems are indistinguishable from ferroelectrics, i.e., ‘reducible’ ferrielectrics, as qualitatively sketched in Fig. 1a. Indeed, CuInP2S6 only shows one paraelectric-ferroelectric transition temperature, and in most cases those geometric ferroelectrics are coined as ‘ferroelectrics’ rather than ‘ferrielectrics’5,9. Similar situations also exist for other ferrielectrics like Pb2MnWO610. Conceptually different to these ‘reducible’ ferrielectrics, in this article, we provide proof of an ‘irreducible’ ferrielectricity (see Fig. 1a for its conceptual definition of ‘irreducible’ ferrielectricity) in BaFe2Se3. We will show unique ferri-characteristics clearly distinguishable from ferroelectricity.

Fig. 1: Concept of ferrielectricity and candidate material BaFe2Se3.
figure 1

a Polarization (P) vs. temperature (T) of ferroelectricity (FE), antiferroelectricity (AFE), reducible-ferrielectricity (r-FiE) and irreducible-ferrielectricity (ir-FiE), respectively. In r-FiE, two polar sub-lattices (A and B) develop synchronously, with one unique critical temperature. This type of ferrielectricity is macroscopically equivalent to ferroelectricity. In ir-FiE, the evolution of sub-lattices A and B is out-of-sync, with two critical temperatures (a higher TC1 and a lower TC2). A compensation point (T0) may appear in some ir-FiE systems. Note that any information on the order of the phase transition is not represented in these qualitative cartoons. b Crystal structure of BaFe2Se3. Each unit is composed of two iron-ladders. c Room temperature structure with a tiny tilting angle between the ladders A and B. d High temperature structure without tilting. The in-situ selected area electron diffraction patterns are shown. The lattice periodicity along the [100] direction changes from 11.90 Å to 5.96 Å as the temperature rises from 298 K to 623 K. e DSC curves indicate two transitions at ~610 K and ~420 K. The ~610 K transition is a second-order one with a step-like behavior, while the ~420 K transition is a first-order one with a peak.

Full size image

Results

BaFe2Se3: ferrielectric material at room temperature

BaFe2Se3 belongs to the iron-based superconductor family11,12,13 but predicted to be multiferroic under ambient conditions14. As shown in Fig. 1b, a BaFe2Se3 u.c. contains two iron ladders (labeled as A and B). Long-range block-type antiferromagnetism (block-AFM) appears below the Néel temperature TN ~ 240–256 K15,16,17,18,19. The structural tetramerization due to the block-AFM leads to charge dipoles along the a-axis and the alignment of dipoles is almost antiparallel but with a tiny canting angle (~5.78° at room temperature) between ladders A and B (schematic displacements are shown in Fig. 1c)14. It should be noted that all other members of the 123-series iron selenides (e.g., BaFe2S3) also own a similar (quasi-) one-dimensional (1D) ladder structure, but only BaFe2Se3 has the canting ladder characteristic. According to theory14, a residual polarization along the c-axis (Pc) is expected in BaFe2Se3, as a characteristic of a ‘reducible’ ferrielectric material.

The tilting of the iron ladders gradually disappears with increasing temperature up to ~600 K, leading to a high symmetric Bbmm phase, according to X-ray diffraction16. Our in-situ selected area electron diffraction (SAED) results give distinctive patterns (Fig. 1c vs. Fig. 1d), confirming the disappearance of the ladder canting at high temperature. Differential Scanning Calorimetry (DSC) measurements (Fig. 1e) confirm the phase transition occurring at ~610 K as a second-order one. Besides, there is a first-order phase transition at ~420 K, which was also evidenced in ref. 16. but its real origin remains a puzzle. In addition, the resistivity behavior also supports this first-order transition (Supplementary Fig. 1). Since our neutron powder diffraction (NPD) data confirm that only one block-AFM transition appears at 250 K, obviously, the transition at ~420 K can be excluded as a magnetic-ordering behavior (Supplementary Fig. 2a).

Using a spherical aberration-corrected scanning transmission electron microscope (Cs-STEM), we were able to determine the subtle structure evolution of the 1D Fe chains, as well as the associated Se’s. Then the structure of BaFe2Se3 can be directly measured atom column by atom column, which reveals an unexpected irreducible ferrielectricity going beyond the theoretical expectations. The STEM image of BaFe2Se3 along b-axis and c-axis was shown in Supplementary Fig. 3. The STEM results at room temperature are summarized in Fig. 2. Interestingly the structural tetramerization already exists at room temperature and, unexpectedly, the intensities for ladders A and B are not equivalent, creating a strong ladder and a weak ladder within a unit cell. The inequivalent features in strong ladders and weak ladders are embodied in magnitude of displacements, as shown schematically in Fig. 2a and in the high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images along the b (Fig. 2b, d) and c axis (Fig. 2c, e). The line profiles along these two ladders are shown in Supplementary Fig. 4. A displacement vector-mapping algorithm was implemented on the cross-sectional HAADF-STEM images to measure the local displacement of the atoms. Based on the statistics of about 300 data for each length, the Fe atoms displacement in the strong ladders are stronger than that in the weak ladders (see Supplementary Fig. 5 for an example). Considering that the Fe-block tetramerization could induce Se ions displacement along the a-axis14 (as clearly indicated in Fig. 2b, d), such inequivalence of Fe displacements will lead to a residual polarization along the a-axis (Pa), which is larger than the expected Pc. The arrow is added to make it more visible. The uncovered zoom-in images (raw data) have been shown in Fig. 2(b, c). Therefore, BaFe2Se3 is a room temperature ferrielectric with polarization mainly along the a-axis, rather than the expected low temperature ferrielectric with polarization along the c-axis14.

Fig. 2: Atomic displacements in the ladders.
figure 2

a Schematic displacements of Fe and Se ions indicated by arrows and amplified in magnitude. Light blue: strong ladder with larger polar bias of Se ions; Dark blue: weak ladder. b, c Color-enhanced HAADF-STEM images of BaFe2Se3 along b-axis and c-axis. The strong and weak ladders are distributed in an alternating order. Scale bar, 1 Å. d, e Superposition of the HAADF image and the polar map of Se atoms along b-axis and Fe atoms along c-axis. The yellow and green arrows there represent the atoms displacements in strong and weak ladders, respectively. Scale bar, 1 nm. f The EELS line scan is across the white line in e. EELS measurements indicate the charge ordering pattern. The averaged Fe L2,3 edge spectrum from neighboring Fe chains is presented. A Fe-L3 peak shift of approximately 0.4 eV between neighboring Fe chain is observed.

Full size image

To explore the origin of this unbalanced ladders, monochromated electron energy loss spectra (mono-EELS) were acquired to demonstrate the underlying charge modulation as shown in Fig. 2f. Using the monochromatror we reach an energy resolution of 0.3 eV, which is enough to detect subtle changes in the fine structure of the EELS excitation edges. The averaged Fe-L3 edges in strong chains and in weak chains show significant differences in their ELNES. Comparing with Fe reference spectra20, the valence states of the strong and the weak chains in BaFe2Se3 are different, and the Fe-L3 peak shift between them is approximately 0.4 eV (shown as the distance between two dashed line in Fig. 2f). Note that the EELS have an ability to reflect a valance change, but the absolute valance identification is still challenging, since the absolute energy position always has several hundred meV uncertainty. Such charge disproportion is not unusual in correlated electron systems, especially in Fe-based oxides and fluorides, e.g., Fe3O4 and LiFe2F621,22, although it has not been reported in selenides before. Nominally, the valences of Fe can become +(2 + δ) and +(2 − δ) for the two sublattices, and a proper δ (around 0.15 according to our fitting results) can lead to the structural tetramerization following the idea of Peierls transition14. It should be noted that the non-integer valences are possible in iron selenides, e.g., in KFe2Se3 and KFe2Se223,24,25. Therefore, charge-ordering, i.e., difference of local electron density, can be the key ingredient for the unbalanced structural tetramerization and affiliated polarization, which needs deeper investigation in future.

Variation of the BaFe2Se3 structure with various temperature

Then it is interesting to know its ferrielectric TC. To characterize the structural tetramerization, the difference (δ) of nearest-neighbor Fe–Fe bond length (d) along the ladder direction is measured as a function of temperature (Fig. 3a). An in-situ heating experiment was performed using a DENSsolutions SH30 system to be able to measure over a wide temperature range. A lamella of BaFe2Se3 was transferred onto specialized chips using a probe-assistance method (Supplementary Fig. 6), then the sample was heated to the set temperature by resistance heating. The displacement vector-mapping algorithm was implemented on the STEM images, and each δ is obtained by averaging around 300 measurements. The difference of Fe–Fe bond length, as well as the tilting angle between the ladders at high temperature vanishes ~600 K, and the in-ladder tetramerization almost drops to zero, implying a high symmetric nonpolar phase (in agreement with the DSC curve shown in Fig. 1e and the X-ray data in ref. 16). The discrepancy between strong and weak ladders disappears in this high symmetric phase, as also demonstrated by above SAED result (Fig. 1d). With decreasing temperature (e.g., at 473 K), unexpectedly, tetramerization emerges in one sublattice of ladders but not in the other, which is a unique characteristic of irreducible ferrielectricity, leading to an emergence of Pa (Fig. 3b) [calculated by density functional theory (DFT)]26. Meanwhile, the ladders become tilting (Fig. 3c compared with Fig. 3d). With further decreasing temperature (e.g., at 423 K), tetramerization emerges in both ladders with different intensities and slopes, implying that the first-order transition occurring at ~420 K corresponds to the starting of tetramerization of the weak ladders. At ~373 K, the intensities of tetramerization are close to identical between both ladders, resulting in an (almost) canceled Pa, i.e., the unique compensation point (T0) of irreducible ferrielectricity. Below T0, the difference between the two ladders increases with decreasing temperature, leading to a reentrance of Pa. It is worth to emphasize that the direction of polarization (i.e., the roles of strong and weak ladders) may be probably reversed across T0 according the tendency (see the last panel of Fig. 1a), although our variable temperature measurements can not continuously track the evolution of individual ladder over so large temperature range. If so, the strong ladder A (weak ladder B) becomes the weak ladder A (strong ladder B) when temperature crossing T0. More color-enhanced HAADF-STEM images acquired at different temperatures along the c-axis are shown in Supplementary Fig. 7. Statistics of the deviation of Fe–Fe bond length in the strong and weak chain at different temperatures could be seen in Supplementary Table 1.

Fig. 3: Temperature-dependent evolution of BaFe2Se3.
figure 3

a The measured structural tetramerization. The light blue and dark blue lines correspond to the strong and weak ladders, respectively. The affiliated arrows denote the corresponding dipoles. b Left axis: the polarization along the a-axis (DFT calculated using the STEM structural data). Right axis: the SHG signal, which mainly reflects the evolution of Pa. The overall evolutions of the polarization and SHG signal qualitatively match. More SHG data and explanation can be found in Supplementary Figs. 8, Fig. 10. c, d Color-enhanced HAADF-STEM images acquired at 298 K and 473 K along the b-axis. The Se atoms displacement in the strong chain is larger than that in the weak chain at 298 K; this is consistent with the difference of the Fe chain evolution magnitude at 298 K. Also, the tilt angle between ladders varies from 5.78° to 1.17° at high temperature. Scale bar, 5 Å. e Simulated evolution of order parameters with a most simplified Landau-type free energy formula. Inserts: the magnified views near the phase transitions, which indicate a second-order transition at TC1 and a first-order transition at TC2.

Full size image

Since the ferrielectric polarization can not be directly measured using electrical methods (and even pizeoelectric force microscopy) in the current stage due to the high leakage of the samples (considering the very small band gap ~0.13–0.178 eV17,18), an optical second harmonic generation (SHG) experiment is employed to characterize the polarity of the materials (see “Methods” section for experimental details). Our SHG signal (Fig. 3b) demonstrates its polarity below ~600 K. Most importantly, the non-monotonic evolution of the SHG signal unambiguously matches the DFT calculated polarization, including the possible compensation point at ~380–400 K, which provides a very strong evidence to support our STEM data.

The irreducible ferrielectricity of BaFe2Se3 can be qualitatively described by Landau theory with a coupling between two ladders (PA and PB). The most simplified free energy formula can be written as:

$$\begin{array}{*{20}{l}}F = a_{\mathrm{A}}\left( {T - T_{\mathrm{A}}} \right)P_{\mathrm{A}}^2 + \beta _{\mathrm{A}}P_{\mathrm{A}}^4 + \gamma _{\mathrm{A}}P_{\mathrm{A}}^6 \\+\,a_{\mathrm{B}}\left( {T - T_{\mathrm{B}}} \right)P_{\mathrm{B}}^2 + \beta _{\mathrm{B}}P_{\mathrm{B}}^4 + \gamma _{\mathrm{B}}P_{\mathrm{B}}^6 + a_{{\mathrm{AB}}}P_{\mathrm{A}}\cdot P_{\mathrm{B}},\end{array}$$
(1)

where the first to six items are the standard Laudau-Ginzburg-Devonshire type energy expression up to the sixth power for sub-lattices A and B, while the last item is the antiferroelectric coupling between two sub-lattices. All coefficients except β2 are positive and the small canting angle between PA and PB is neglected. Without fine tuning of the coefficients (see “Methods” section for details), the simulated evolution of the polarization (Fig. 3e) is qualitatively reproducing the non-monotonic experimental behavior, implying the correct main physics captured in the model. Consistent with the DSC data, the high temperature transition is a second-order one, while the low temperature transition is a first-order one due to the negative β2.

Manipulation of BaFe2Se3 by an external electric field

As a polar material, electric field tuning of the polarization is a fundamental function. However a direct measurement of the electric hysteresis loop is technically challenging in the current stage due to serious leakage, but we have successfully developed an inspiring in-situ technique to manipulate the polar structure at an atomic scale by applying an electric field. An electrical bias was applied between a tungsten tip, which acts as a mobile electrode, and the lamella of BaFe2Se3, which is connected to ground (as schematically shown in Fig. 4a). To capture the changing of atoms positions, the real-time crystal structure with atomic-scale spatial resolution was characterized in STEM mode; the access to dynamic structural information provide a clear picture of the evolution under an external electric field. As shown in Fig. 4b, c and Supplementary Fig. 9, the tetramerization is significantly enhanced by applying an electric field along the a-axis. This implies a significant enhancement of polarization under the electric field. However, the reversal of Pa has not been achieved, implying a large coercive field.

Fig. 4: Manipulation of the ferrielectric polarization in BaFe2Se3.
figure 4

a Schematic diagram of the electric field experiment. The in-situ biasing experiment was performed with an input voltage VDC = 5 V. To capture the structural changes, a real-time analysis is performed in STEM mode. b, c Comparison of the local dipoles with/without applied voltage. The arrows denote the displacements of 50% of the Fe ions, while the rest of the Fe ions are treated as reference points. The difference between the strong/weak ladders is further enhanced by the electric field. Arrows are added to make the displacements more visible. The uncovered zoom-in image (raw data) can be found in Fig. S9. Scale bar, 5 Å.

Full size image

Previous experiments reported the space group Pnma for BaFe2Se3 at room temperature15,16,17, which is nonpolar and does not allow the tetramerization. A recent work reported the space group Pmn21 (a subgroup of Pnma) at room temperature, allowing the tetramerization and polarization27. Another recent X-ray diffraction work reported the space group Pmn21 at 300 K but Pm (a subgroup of Pmn21 allowing the inequivalent ladders) at 150 K28. In fact, the patterns of NPD (or X-ray) are very subtle among these space groups (see Supplementary Fig. 10 and Supplementary Fig. 11), which thus can not distinguish these structures precisely. Instead, our STEM technique is more suitable to monitor these subtle distortions of inner coordinates. According to our studies, below TC1 the accurate space group should already be Pm, allowing the asymmetry between two ladders. The transition from Bbmm to Pm at TC1 is a second-order one while the first-order transition at TC2 does not change the symmetry. Other high-resolution technique, such as synchrotron X-ray diffraction, may be helpful to verify our STEM results in future.

Discussion

Finally, it should be noted that the irreducible ferrielectrics is not limited to BaFe2Se3 but with broader interests. For example, as an important branch of multiferroics, TbMn2O5 and other 125-type manganites showed strange ‘ferroelectric’ behavior of polarization as a function of temperature or magnetic field29,30, including the compensation point of polarization. The real mechanism is that the ferroelectric contributions in TbMn2O5 are from three out-of-sync sources according to the SHG measurement30.

Even though, our current work on BaFe2Se3 is not a marginal extension of TbMn2O5. The polarity in TbMn2O5 is magnetism-driven, i.e., it is a so-called type-II multiferroic material, instead of a proper ferroelectric material. It is not rare for a magnetic system to have sequential magnetic phase transitions. In this sense, the nontrivial evolution of polarization in TbMn2O5 is just a secondary effect of magnetic evolution, which occurs at very low temperature (<40 K) and gives a very weak signal of polarization (~<0.04 μC/cm2 and ~<0.15 μC/cm2)29,30. In our case, the ferrielectricity is not magnetism-driven but a primary polar property, which occurs above room-temperature (15 times of TbMn2O5) and with a much larger polarization (5–15 times of TbMn2O5). In addition, limited by its very weak polarization signal, the experimental measurements of TbMn2O5 can only rely on the pyroelectric method, which can lead to a net polarization but the microscopic facts of different contributions were mostly by suspecting or indirect derivation from SHG signals. Instead, our current work, powered by the advanced in-situ STEM techniques and thanks to the strong signal of BaFe2Se3, the microscopic evolution of two contributions can be visualized directly, leading to a more decisive conclusion. In fact, although the nontrivial polarization of TbMn2O5 has been known for decades, it is more likely to be recognized as a type-II multiferroics with strange ferroelectric behavior. Our work will lead to a re-look at the irreducible ferrielectricity, including that in TbMn2O5.

The irreducible ferrielectricity combines both characteristics of ferroelectricity and antiferroelectricity, making these systems having more degrees of freedom to be controlled. For example, by tuning the amplitudes of sub-lattice polarizations near the compensation point, the macroscopic polarization can be easily switched, without the reversal process of dipole moments as required in ferroelectric cases. Moreover, complex ferroelectric+antiferroelectric domain structures may be expected in ferrielectrics31, which deserve further studies.

In summary, employing spherical aberration-corrected STEM with sub-angstrom resolution, the structural evolution of BaFe2Se3 has been characterized in detail. Highly interesting phenomena, beyond previous experimental observations and theoretical predictions, have been detected and analyzed. First, BaFe2Se3 is a room temperature polar material. Second, combined with EELS analysis, the origin of its structural tetramerization is demonstrated to be driven by the local electron density, not the previously expected block-type antiferromagnetism. Third, most importantly, the evolution of the two ladders in BaFe2Se3 does not behave synchronously, leading to irreducible ferrielectricity. The compensation point, a unique fingerprint of irreducible ferrielectricity, is observed. The irreducible ferrielectricity reported here is conceptually different from previously reported reducible ferrielectricity which is actually equal to ferroelectricity. The irreducible ferrielectricity in BaFe2Se3 acts as the primary effect, leading to a stronger impact to the community to re-investigate this independent branch of polarity. More functionalities are promisingly expected in future based on irreducible ferrielectricity, e.g., the magnetic-field-tunable polarization as demonstrated in TbMn2O5.

Methods

Material synthesis

High-quality BaFe2Se3 single crystals were grown by the self-flux technique starting from an intimate mixture of Ba pieces, Fe granules, and Se powders with an atomic ratio of 1:2:3. Then the starting materials were put in a carbon crucible and sealed in the quartz tube with partial pressure of argon. The quartz tube was first heated to 420 °C at a rate of 1 °C/min, held for 12 h, and then annealed at 1150 °C for another 24 h. After that, the quartz tube was slowly cooled down to 750 °C at a rate of 3 °C/h. Finally, the quartz tube was cooled down to room temperature naturally and the strip-like BaFe2Se3 single crystals with a typical size of 3.0 × 1.0 × 0.5 mm3 and shiny surfaces can be obtained.

Macroscopic properties measurements

Differential scanning calorimetry (DSC) experiments were performed with Maia DSC 200 F3. Measurements were performed on heating and cooling with a rate of 10 K·min−1. The sample is encapsulated in a standard Al crucible using argon stream as the protecting gas. XRD measurements were performed on Rigaku Smartlab3 with Cu Kα radiation. In the SHG measurements, the incident laser with a wave length of 800 nm is perpendicular to the cleavage (100) plane and the reflected light at 400 nm is collected. The polarization of the incident laser is controlled by a half wavelength plate. Then the canting polarization along the c-axis can be monitored, which is in proportional to the main component of polarization along the a-axis. The SHG signal in Fig. 3b was measured with the polarization of the incident laser (i.e., the electric field component E) in the bc cleavage surface (Fig. S10c) of the BaFe2Se3 crystal, while the angular-dependent results with rotating E can be found in Fig. S8. Magnetic measurements were carried out in a vibrating sample magnetometer (VSM) integrated in a Physical Property Measurement System (PPMS-9, Quantum Design) up to 600 K. Neutron Powder Diffraction (NPD) data were collected on a High-intensity Powder Diffractometer Wombat at Australian Nuclear Science and Technology Organization (ANSTO) with λ = 2.41 Å, between 10 K and 500 K. Resistivity was measured using Keithley 4200A-5CS.

Conventional and scanning transmission electron microscopy

Samples was cut into lamellas by Focused Ion Beam (FEI Quanta 3D FEG) for the observation of electron microscope. We use spherical aberration correction electron microscopy (FEI Titan G2 80–200 ChemiSTEM, 30 mrad convergence angle, 0.8 Å spatial resolution) to acquire atomic resolution HAADF-STEM images of BaFe2Se3’s cross section from different directions and the image noise was corrected using Digital Micrograph. All STEM images in this work are filtered in Fourier space using a grid mask to select for the lattice frequencies and by low and high pass annular filters to remove the zero frequency and high frequency noise above the information transfer limit. Electron Energy Loss Spectroscopy (EELS) test was also performed on BaFe2Se3 to verify whether there are changes in the valence state of iron. SAED patterns (selected area electron diffraction) obtained on FEI Tecnai G2 F20 S-TWIN are used to verify the analysis on the local evolution in the statistical sense. Some additional details should be mentioned: (1) As to exclude the influence of microscope artifacts, some steps have been taken. To minimize the influence of sample drift, most of the microscopy data for quantitative analysis are acquired under the condition of drift below 1 Å min−1. (2) The STEM image were acquired from the mutually perpendicular directions, and the analysis results of bond length show no obvious difference between them. Thus, the possibility of STEM scanning direction as the main origination of the observed phenomenon can be excluded. (3) High frequency vibration of imaging would be another potential influence factor. Therefore, a technique of ultra-fast acquirement was employed. Tens of images were quickly acquired in the same local region, and most HAADF images shown in this article are overlaid based on such image series, the effect of the specimen drift and beam vibration were significantly reduced and the signal-to-noise ratio of the HAADF images was improved, simultaneously. (4) Aiming at avoiding oxidation, experiments were performed as soon as BaFe2Se3 was taken out of glove box which offer protecting gas. (5) In consideration of that potential slight damage caused by ion beam in FIB, we minished parameters including voltage and electric current of ion beam down to 2 kV/27 pA to minimize the negative and unnecessary surface damage. For BaFe2Se3, the antiferromagnetic ordering temperature is 250 K (Supplementary Fig. 2), while most of STEM data are measured far above this temperature. Thus, the magnetic fields (from Cs-STEM) effect to polar distortion is negligible in the high temperature paramagnetic region.

In-situ study

The in-situ heating experiment was done on DENS solutions SH30 system in order to carry out the experiment in a wide temperature range. The Nano-Chip we used could control the temperature environment locally on the device via the 4-point-probe. Its highest temperature accuracy and stability is 0.001 °C. The experimental data at low temperature was obtained by a demo low-temperature sample holder made by DENS. The in-situ biasing was done on Hysitron PI-95 TEM Picolndenter, the input voltage VDC = 5 V was applied between the sharp conductive tip and the sample using a function generator. To capture the changing of atoms positions, the real-time crystal structure is characterized in STEM. The atomic-scale spatial resolution of STEM and the access to structural information provide a clear picture of the evolution under external electric field.

Specimen transfer onto biasing chips

To measure the performance of BaFe2Se3, as shown in Supplementary Fig. 6. After conventional FIB process of welding the lamella onto needle and transfer it near the surface of chips, additional confined Pt pad was deposited to contact the lamella onto the chip surface. The lamella thickness was to about 2 μm. Low current down to 10 pA was used to polish the surface of chips after detaching the needle to reduce the amount of redeposited material resulting from the previous contacting process.

DFT calculation

The DFT calculation was performed based on the projector augmented-wave (PAW) potentials and Perdew-Burke-Ernzerhof exchange function as implemented in Vienna ab initio simulation package (VASP)32,33,34. The plane-wave energy was 500 eV. The experimental structures at different temperatures were used and the Cx-type antiferromagnetism is adopted for simplify (since here the polarization is not driven by magnetism). Brillouin zone integration was obtained using a 6 × 3 × 4 k-point mesh. The standard Berry phase method is adopted to estimate the ferroelectric polarization35, while the intuitive point-charge-model provides similar results.

Laudau-Ginzburg-Devonshire model

To fit the experimental phase transitions, TA = 610 K and TB = 420 K, are used. Noting TC1 = TA for the second order phase transition, and TC2 is close but slightly higher than TB for the first order transition. To simulate Fig. 3e, α1 = 1 as the unit, and β1 = 5, α2 = 4.5, β2 = −5, γ1 = γ2 = 40. The negative β2 is essential for the first-order transition around TC2 and the differences between α1/α2, β1/β2 originate from the charge disproportion. α12 can be a small quantity, e.g., 0.001.

Determining the position of atoms

Polarization mapping here was performed by calculating ion displacements in HAADF-STEM images. On account of the fact that the bright area of every atom in HAADF image is actually too large for us to determine where the center of atom is, a mathematical method involving Gaussian Fitting based on Matlab is essential to ascertain the accurate position of every atom. Gaussian Fitting could give an accurate position of atom according to the brightness of every atom.

Determining atomic positions by fitting each atom site using a spherical Gaussian algorithm in Matlab is a common method. For double-check of our conclusions, we used two different softwares: CalAtom36,37 and StatSTEM38 and compare their calculating results. The average value distribution of data using these two softwares are keeping an exact consistency. For example, for the Fe–Fe bond length of strong ladder at room temperature, CalAtom reveals that they are 2.71 Å and 2.55 Å; the StatSTEM reveals that they are 2.72 Å and 2.54 Å Besides, each bond length acquired from atoms-position-determination software are based on the statistics value of about 300 data, thus they are statistically meaningful. Furthermore, multiple images were recorded for most of the data we exhibit. The multiple images were averaged in order to reduce noise and artifacts induced by possible random drifts of the sample. In the average procedure, the aliment of these images was done by minimizing the shift of an individual image relative to the averaged image using an iterative rigid alignment method. Another methods to measure the artifacts in STEM images is to determine the displacements of atoms in which no off-center displacements would happen39. On the basis of this method, Lu, L. et al. measured the STO layers39 with rms = 4.8 pm, we observed the STO layers with rms = 3.2 pm using CalAtom software.