Dynamical and thermal magnetic properties of the Kitaev spin liquid candidate α-RuCl₃

Abstract

What is the correct low-energy spin Hamiltonian description of $\alpha$-RuCl$_{3}$? The material is a promising Kitaev spin liquid candidate, but is also known to order magnetically, the description of which necessitates additional interaction terms. The nature of these interactions, their magnitudes and even signs, remain an open question. In this work we systematically investigate dynamical and thermodynamic magnetic properties of proposed effective Hamiltonians. We calculate zero-temperature inelastic neutron scattering (INS) intensities using exact diagonalization, and magnetic specific heat using a thermal pure quantum states method. We find that no single current model satisfactorily explains all observed phenomena of $\alpha$-RuCl$_{3}$. In particular, we find that Hamiltonians derived from first principles can capture the experimentally observed high-temperature peak in the magnetic specific heat, while overestimating the magnon energy at the zone center. In contrast, other models reproduce important features of the INS data, but do not adequately describe the magnetic specific heat. To address this discrepancy we propose a modified ab initio model that is consistent with both magnetic specific heat and low-energy features of INS data.

Introduction

Quantum spin liquids (QSL) are long-sought-after states of matter without magnetic order, but with nontrivial topological and potentially exotic properties.^1,2 Much of the search has been focused on frustrated lattice systems,^3,4 but in an important development in 2006 Kitaev⁵ introduced a novel exactly solvable paradigmatic QSL with bond-directional Ising terms on the bipartite honeycomb lattice. Importantly, this Kitaev model hosts anyonic excitations,⁶ which are of interest both for fundamental reasons and for their proposed application in topological quantum computing.^7,8 It was realized that such interaction terms naturally appear⁹—and can be large—in Mott-insulating transition-metal systems with edge-sharing octahedra and strong spin-orbit coupling, such as in A$_{2}$IrO$_{3}$ (A = Na, Li),^10,11$\alpha$-RuCl$_{3}$¹² and other materials.^13,14

However, the three mentioned materials are all found to order magnetically at low temperatures, and hence cannot be perfect realizations of the Kitaev model. Na$_{2}$IrO$_{3}$^15,16,17 and $\alpha$-RuCl$_{3}$^18,19,20,21 both develop a zigzag order, as illustrated in Fig. 1a, while Li$_{2}$IrO$_{3}$ displays an incommensurate spiral order.²²

Fig. 1: $\alpha$-RuCl$_{3}$.

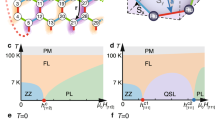
a The zigzag magnetic order. b The honeycomb lattice and its different bonds. Solid, dotted and dashed lines represent nearest, second-nearest and third-nearest-neighbor bonds, respectively. c The variability in two nearest-neighbor (NN) parameters between various proposed spin Hamiltonians for $\alpha$-RuCl$_{3}$. The Hamiltonians marked by red, bold numbers (blue, roman) are discussed in the main text (Supplementary Information). Here ${K}_{1}$ and ${J}_{1}$ are the NN Kitaev and Heisenberg couplings, respectively, and ${\Gamma }_{1}$ is an NN symmetric off-diagonal interaction. Models with ferromagnetic (antiferromagnetic) ${K}_{1}$ are marked with crosses (open circles). Bond-averaged values were used for anisotropic models.

Despite the zigzag order, $\alpha$-RuCl$_{3}$ has emerged as a particularly promising Kitaev QSL candidate. Initial strong evidence came in the form of a strong and unusually stable scattering continuum at the zone center as observed in inelastic neutron scattering experiments (INS),^23,24,25,26 which has been interpreted as evidence for the presence of fractional Majorana excitations. However, in an alternative picture it has been proposed that the continuum may consist of incoherent excitations due to spontaneous magnon decays.²⁷ More recently, half-integer quantization of the thermal Hall conductivity was reported,²⁸ also consistent with Majorana excitations. The quantization occurs in a narrow range of in-plane magnetic fields, where the magnetic order is melted, possibly uncovering an intermediate QSL state.^{24,29,30,31,32} Further evidence for Kitaev physics has been found in experiments reporting magnetic specific heat,^25,33,34 NMR,^30,35 microwave absorption,³⁶ Raman scattering,^37,38,39 and THz spectroscopy results.^40,41,42,43

Altogether, these experiments strongly suggest that $\alpha$-RuCl$_{3}$ can be described by a generalized Kitaev-Heisenberg Hamiltonian,^13,14 including off-diagonal and further-range interactions. Theoretical work leads to the same picture, whether the model is deduced from ab initio methods,^{12,44,45,46,47,48,49,50} or from more phenomenological or ab initio-inspired approaches.^27,51,52,53 Unfortunately, these different works, as well as experimental fits,^26,40 have led to a veritable zoo of proposed realistic spin Hamiltonian descriptions for $\alpha$-RuCl$_{3}$, and it is not currently clear which description is most accurate. Moreover, the proposed models disagree in terms of included spin–spin interaction terms, magnitudes of interaction parameters, and even signs. We illustrate this situation in Fig. 1c by a scatter plot of the values for just two relevant interaction terms, and in Table 1.

Table 1 The spin Hamiltonians for $\alpha$-RuCl$_{3}$ considered in this work.

In this work, we adopt a systematic approach to address this uncertainty. We calculate static spin structure factors (SSFs) $S\left({\bf{q}}\right)$ and INS intensities $I\left({\bf{q}},\omega \right)$ for all models listed in Table 1 using Lanczos exact diagonalization (ED)⁵⁴ on 24-site clusters. We also use ED to explore the evolution of the INS spectra away from the ferromagnetic Kitaev limit as new perturbations are introduced in a generalized Kitaev-Heisenberg model. We then calculate the magnetic specific heat ${C}_{{\rm{mag}}}$ for the models using the thermal pure quantum state (TPQ) method⁵⁵ on the 24- and 32-site clusters shown in Fig. 2. A few of the models considered here have previously been studied using similar methods in refs. ^27,53,56. For clarity we will restrict the discussion in the main text to six particularly relevant models. These models all have a ferromagnetic Kitaev coupling (${K}_{1}\,<\,0$), which is expected in $\alpha$-RuCl$_{3}$.^13,14 Results for the other models are included in the Supplementary Information.

Fig. 2: Clusters.

a, b Finite size clusters with periodic boundary conditions, and c the first and second Brillouin zones for the honeycomb lattice. Arrows indicate the high-symmetry path used for $I\left({\bf{q}},\omega \right)$ spectra.

Our key finding is that none of the studied models manages to fully capture the salient features of both the INS and magnetic specific heat data. The energy scales obtained in first principles approaches appear to be needed to reproduce a high-temperature peak in ${C}_{{\rm{mag}}}$, but the parameters proposed in the literature push the INS intensity at the $\Gamma$ point to higher energies. On the other hand, models obtained by fits to INS data run the risk of missing significant off-diagonal interactions, and fail to reproduce the experimentally observed temperature dependence of ${C}_{{\rm{mag}}}$. By modifying one of the ab initio models, we are able to find results consistent with both ${C}_{{\rm{mag}}}$ and low-energy features of the INS spectrum. Our results thus provide important clues for an accurate and realistic description of of $\alpha$-RuCl$_{3}$.

Results

Several of the Hamiltonians listed in Table 1 are special cases of a proposed minimal model^13,47 for $\alpha$-RuCl$_{3}$,

$${H}_{{J}_{1}-{K}_{1}-{\Gamma }_{1}-{J}_{3}}=\sum _{\langle i,j\rangle }\left[{J}_{1}{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}+{K}_{1}{S}_{i}^{\gamma }{S}_{j}^{\gamma }+{\Gamma }_{1}\left({S}_{i}^{\alpha }{S}_{j}^{\beta }+{S}_{i}^{\beta }{S}_{j}^{\alpha }\right)\right]+{J}_{3}\sum _{\langle \langle \langle i,j\rangle \rangle \rangle }{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j},$$

(1)

where $\langle \ldots \rangle$ and $\langle \langle \langle \ldots \rangle \rangle \rangle$ denote nearest and third-nearest neighbors, respectively. $\gamma =$X, Y, Z is the bond index shown in Fig. 1b, and $\alpha ,\beta$ are the two other bonds. The ${\Gamma }_{1}$ term is required to explain the moment direction, and ${J}_{3}\,>\,0$ helps stabilize the zigzag order. Ab initio and DFT studies also tend to report a sizable symmetric off-diagonal ${\Gamma }_{1}^{^{\prime} }$ interaction,

$${H}_{{\Gamma }_{1}^{^{\prime} }}={\Gamma }_{1}^{^{\prime} }\sum _{\langle i,j\rangle }\sum _{\alpha \ne \gamma }\left[{S}_{i}^{\gamma }{S}_{j}^{\alpha }+{S}_{i}^{\alpha }{S}_{j}^{\gamma }\right],$$

(2)

which originates from trigonal distortion.^57,58 Since the crystal structure of $\alpha$-RuCl$_{3}$ features trigonal compression^13,19,20,25 perturbative calculations^47,58 would predict that ${\Gamma }_{1}^{^{\prime} }\,<\,0$, which provides an additional mechanism to stabilize the zigzag order.^58,59 In the absence of other crystal distortions, the most general nearest-neighbor Hamiltonian would thus be the ${J}_{1}-{K}_{1}-{\Gamma }_{1}-{\Gamma }_{1}^{^{\prime} }$ model. Combining these two proposed minimal models results in the ${J}_{1}-{K}_{1}-{\Gamma }_{1}-{\Gamma }_{1}^{^{\prime} }-{J}_{3}$ model.

Further proposed extensions include second-nearest-neighbor Kitaev and Heisenberg terms, third-nearest-neighbor Kitaev terms, and additional symmetry-allowed anisotropies.^44,47 In particular, $\alpha$-RuCl$_{3}$ does not have a perfect honeycomb lattice, which allows the parameters for the Z bond to deviate from those on the X, Y bonds. In Table 1 we have bond averaged such anisotropies for the sake of clarity, but we will use the full parameter sets in our calculations when appropriate.

Spin structure factors and neutron scattering intensities

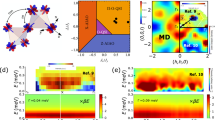
Figure 3 shows predicted zero-temperature neutron scattering intensity spectra, $I\left({\bf{q}},\omega \right)$, for the six central models. All models feature sharp low-frequency peaks at the M points, indicating the zigzag order. The intensity at the M points is significantly higher than the intensity at the $\Gamma$ point, which is inconsistent with experimental observations.²⁴ However, the M peaks could potentially be suppressed at finite temperatures.⁵¹ The models in Fig. 3b–e all show clear signs of the scattering continuum at the $\Gamma$ point at frequencies comparable to the position of the M peak, whereas the two ab initio models in (a) and (f) display a sizable gap up to any noticeable scattering at the $\Gamma$ point.

Fig. 3: INS spectra.

Inelastic neutron scattering intensities $I\left({\bf{q}},\omega \right)$ for the chosen models calculated at zero temperature using the $N=24$ site cluster. The model shown in (f) was bond averaged.

In the top row of Fig. 4 we have plotted the static spin structure factors $S\left({\bf{q}}\right)$. As shown, all six models are consistent with a zigzag ordering with some weight at the zone center. The model shown in Fig. 4d showcases how different interaction strengths for the Z bond results in weakly broken ${C}_{3}$ symmetry in the structure factors. The bottom three rows of Fig. 4 shows integrated INS intensities for three different energy windows. Experimentally, a star-like pattern with strong weight at $\Gamma$ and arms extending to the M points was observed in the $\omega \in [4.5,7.5]$ meV energy window.²³ We dub this pattern the M star. The only model displaying this pattern in the right energy window is the one due Yadav et al.⁴⁸, in Fig. 4e. In contrast, (b), (c), and (d) have star-like patterns where the arms extend towards the K points—K star shapes. The two ab initio models in (a) and (f) do not capture the weight at $\Gamma$ at all, instead forming a flower-like shape that we would expect to see for lower frequencies, since the peak at $\Gamma$ is observed to be higher energy than the M point peak (2.69 ± 0.11 meV vs. 2.2 ± 0.2 meV from INS data.²⁴) The high-energy window $\omega \in [10.5,20.0]$ meV is expected to be dominated by the continuum at $\Gamma$, which is consistent with (b), (c), (d), (e), but not the “lotus root-like” shapes in (a), and (f).

Fig. 4: Additional inelastic neutron scattering intensity results obtained on the $N=24$ site cluster.

The top row shows the static spin structure factors as a heatmap over $k$-space. The dashed white hexagon marks the first Brillouin zone, and the outer red hexagon shows the second Brillouin zone. The three lower rows show the neutron scattering intensities $I\left({\bf{q}},\omega \right)$ integrated over representative energy windows (i) [1.3, 2.3] meV, (ii) [4.5, 7.5] meV, and (iii) [10.5, 20.0] meV. Note that each heatmap is normalized separately, in order to showcase patterns in momentum space. Intensities in different heatmaps should not be compared.

We summarize our computed neutron scattering intensity results in Table 2, which also includes results for the models discussed in the Supplementary Information. The ab initio-inspired approach of Winter et al.²⁷ was constructed to reproduce certain features in the INS spectrum, and thus does particularly well. It reproduces the $\Gamma$ point intensity profile well (see Supplementary Fig. 3), and has an M star shape in the [5.5, 8.5] meV window, but not in [4.5, 7.5] meV. It is thus natural to use this model as a starting point for INS data-compatible effective Hamiltonians, as done in the THz spectroscopy fit of ref. ⁴⁰, and an analysis of the magnon thermal Hall conductivity in ref. ⁵². The latter work (for results see the Supplementary Note 3) proposes a particularly minor change—only reducing the magnitude of ${J}_{3}$ from 0.5 meV to 0.1125 meV while keeping other parameters fixed—which actually leads to an M star shape in the relevant window, but also significantly alters the intensity profile at the $\Gamma$ point. We mention this fact explicitly as an example of a more general observation: for these models even small changes to the parameters can result in significantly different spectra, while even significantly different models can produce very similar SSFs and the same magnetic order. This difficulty calls for other methods to constrain the possible effective Hamiltonians, which is why we will later study the magnetic specific heat.

Table 2 Summary of results, highlighting important features in the INS and magnetic specific heat predictions on the 24-site cluster.

Evolution of INS spectra

Above we have provided results for spin Hamiltonians with multiple interaction parameters. To untangle the roles and effects of different interaction terms, we now focus on a minimal ${J}_{1}-{K}_{1}-{\Gamma }_{1}-{\Gamma }_{1}^{^{\prime} }-{J}_{3}$ model. We fix the energy scale $1=\sqrt{{J}_{1}^{2}+{K}_{1}^{2}+{\Gamma }_{1}^{2}+{\left({\Gamma }_{1}^{^{\prime} }\right)}^{2}+{J}_{3}^{2}}$, and use a hyperspherical parametrization where

$${\Gamma }_{1}=\cos \theta ,$$

(3)

$${J}_{1}=\sin \theta \cos \phi ,$$

(4)

$${K}_{1}=\sin \theta \sin \phi \cos \chi ,$$

(5)

$${\Gamma }_{1}^{^{\prime} }=\sin \theta \sin \phi \sin \chi \cos \psi ,$$

(6)

$${J}_{3}=\sin \theta \sin \phi \sin \chi \sin \psi$$

(7)

When $\chi =0$ this reduces to the notation used in ref. ⁵⁷. Following the typical hierarchy of interaction strengths in Table 1 ($| {K}_{1}| \ge | {\Gamma }_{1}| \ge | {J}_{1}| \sim | {\Gamma }_{1}^{^{\prime} }| \sim | {J}_{3}|$) we begin by assuming a dominant FM Kitaev interaction, and introduce other terms one by one. A representative selection of the resulting spectra is shown in Fig. 5. Additional parameter values are studied in Supplementary Note 5.

Fig. 5: Evolution of the INS intensity $I\left({\bf{q}},\omega \right)$ away from the ferromagnetic Kitaev limit.

The limit is shown in a. In b, c a ${\Gamma }_{1}\,>\,0$ term is added. The cases of AFM ${J}_{1}$ and FM ${J}_{1}$ are considered in d, e, respectively. Finally ${\Gamma }_{1}^{^{\prime} }\,<\,0$ and ${J}_{3}\,>\,0$ are introduced in f, g. These results were obtained using the 24-site cluster.

As Fig. 5a shows, the FM Kitaev limit has a flat spectrum with intensity peaked at the $\Gamma$ point, consistent with the exact theoretical result.⁶⁰ The spectral evolution away from this point can be qualitatively understood using previously obtained phase diagrams.^57,58 For ${\Gamma }_{1}/{K}_{1}=-1/2$ shown in Fig. 5b, a sharp low-energy peak develops at the center point between $\Gamma$ and K$_{1}$, “K$_{1}/2$”, signaling a tendency toward spiral order. The peak at the $\Gamma$ point remains strong, however, preventing a clear signal of the spiral phase in the static spin structure factor. We also note that the resolution of the spiral phase ordering vector is limited by the finite cluster size, and that some zigzag correlations remain at the M points. As ${\Gamma }_{1}$ is increased to ${\Gamma }_{1}/{K}_{1}=-1.0$ in Fig. 5c the intensities at K$_{1}/2$ and the M points become comparable in strength. As can be seen by comparison with the Kitaev limit, the presence of ${\Gamma }_{1}\,>\,0$ in (b) and (c) tends to produce a stronger excitation continuum, that stretches to higher frequencies.

We next introduce the nearest-neighbor Heisenberg exchange ${J}_{1}$. Figure 5d, e show the effect of adding antiferromagnetic and ferromagnetic ${J}_{1}$, respectively (${J}_{1}/{K}_{1}=\mp 0.1$). In this case ${J}_{1}\,>\,0$ produces a stronger peak at K$_{1}/2$ and weaker intensity at the $\Gamma$ point, signaling a stabilized spiral order phase. This is consistent with the classical phase diagram of ref. ⁵⁷ and cluster mean field theory results of ref. ⁵⁹. In contrast, ${J}_{1}\,<\,0$ sees the peaks at the $\Gamma$ point move down in frequency, a strengthening of the M peaks and significant reduction in intensity at K$_{1}/2$. These observations are consistent with moving into the regime of ferromagnetic ordering. We note that a strong continuum remains at the zone center. In the case of ${\Gamma }_{1}/{K}_{1}=0$ we would have had a weaker continuum, and a stronger low-energy peak at the zone center. Finally we also introduce ${\Gamma }_{1}^{^{\prime} }\,<\,0$ and ${J}_{3}\,>\,0$ in Fig. 5f, g. These interactions both stabilize the zigzag order, while pushing the $\Gamma$ point peaks to higher frequency, and generally weakening the continuum nature of the excitation spectra. This suggests that the unrealistically large gaps at the $\Gamma$ points in Fig. 3a, f may be due to an overestimation of the ${\Gamma }_{1}^{^{\prime} }$ and ${J}_{3}$ parameters.

Magnetic specific heat

As shown in Fig. 6a, the magnetic specific heat of the pure Kitaev model features two characteristic, well-separated peaks at ${T}_{{\rm{l}}}$ and ${T}_{{\rm{h}}}$, where the low-$T$ one is due to thermal fluctuations of localized Majorana fermions, and the high-$T$ peak is related to itinerant Majoranas.^61,62 This two-peak structure appears to be stable to small perturbations away from the Kitaev point.^6,63,64 Note that the presence of two peaks is not itself a unique signature of Kitaev physics^63,65 and occurs also for e.g., the $\Gamma$ model,^64,66 see Fig. 6a.

Fig. 6: Magnetic specific heat calculated using the TPQ method and the $N=24$ site cluster.

The solid lines show the average value over $15$ initial vectors (100 vectors were used for the $\Gamma$ model), and the shaded areas show the standard deviation. a shows ${C}_{{\rm{mag}}}$ for the ferromagnetic Kitaev (${K}_{1}=-1$), ferromagnetic Heisenberg (${J}_{1}=-1$), and “antiferromagnetic” Gamma (${\Gamma }_{1}=+1$) models. b, c show ${C}_{{\rm{mag}}}$ for the six chosen models for $\alpha$-RuCl$_{3}$. For comparison, the experimentally determined excess heat capacity from ref. ³⁴ is plotted using black dots. The peak in the experimental data near 6.5 K signals the magnetic ordering, and the strong peak at 170 K is a structural transition, unrelated to the magnetic specific heat. Finally, the peak near 70 K may correspond to itinerant Majorana quasiparticles.^34,61,62 The peak position is inconsistent with the models plotted in b, but consistent with the ab initio models plotted in c, with higher interaction strengths.

A similar two-peak structure has been found in $\alpha$-RuCl$_{3}$ experiments, using both RhCl$_{3}$³⁴ and ScCl$_{3}$^25,67,68 as nonmagnetic analogue compounds. In clean samples, a sharp low-$T$ peak representing the magnetic ordering occurs at ${T}_{{\rm{l}}}\approx 6.5$ K,^30,34 and then a broader peak occurs at a higher temperature ${T}_{{\rm{h}}}$, followed by a (nonmagnetic) structural transition of $\alpha$-RuCl$_{3}$ near 165–170 K.^25,34 So far, there is no clear consensus for the precise value of ${T}_{{\rm{h}}}$ (Widmann et al. report ${T}_{{\rm{h}}}\approx 70$ K,³⁴ Do et al. find ${T}_{{\rm{h}}}\simeq 100$ K,²⁵ while Hirobe et al.⁶⁷ and Kubota et al.⁶⁸ find a broad maximum around 80–100 K), but it appears to be an order of magnitude larger than ${T}_{{\rm{l}}}$. Whether or not the ${T}_{{\rm{h}}}$ peak can be attributed to fractionalized excitations due to a proximate Kitaev QSL, the feature appears to be real and ought to be captured by a realistic spin Hamiltonian. Two additional comments are in order. First, accurately determining the magnetic specific heat at higher temperatures is challenging, and sensitive to details of the analysis. This may partly explain the range of ${T}_{{\rm{h}}}$ values mentioned above. Second, an optical spectroscopy study⁶⁹ extracted a crossover temperature for magnetic correlations, ${T}^{\star } \sim 35$ K, which, in an analysis relying on the pure Kitaev model, was equated to ${T}_{{\rm{h}}}$. In the following we will rely mainly on data from Widmann et al.,³⁴ but there is clearly some uncertainty to the value of ${T}_{{\rm{h}}}$.

In Fig. 6b, c we plot the magnetic specific heat, ${C}_{{\rm{mag}}}(T)$, for the six considered models on 24-site clusters, along with the excess heat capacity determined in ref. ³⁴. We note that the finite-size clusters are far from the thermodynamic limit, so we cannot expect to numerically observe a sharp magnetic transition, but the location of the peaks can provide useful information. We see that the models plotted in (b) are clearly inconsistent with the experimental data. However, the two ab initio models in (c) (which did not capture the INS data) actually have peak positions that are consistent with the data. In fact, the model fully determined from first-principles in Eichstaedt et al.⁴⁴ has a peak at ${T}_{{\rm{h}}}\approx 66$ K, while the experimental data are centered around 70 K, with a peak at 68 K.

In Fig. 7 we provide 32-site cluster TPQ results for a subset of the models, and show the finite-size scaling tendencies. The two cluster sizes have different symmetry properties, which could explain part of the differences. Unfortunately, going to even larger cluster sizes (for better scaling or to preserve symmetries) using the TPQ method becomes computationally prohibitive. We find that the position of the high-temperature peak changes only marginally (see Supplementary Note 2 for details), while the low-temperature behavior is much less well-converged. We thus conclude that the two ab initio models describe the magnetic specific heat better than the other models.

Fig. 7: Finite size scaling of specific heat for four select Hamiltonians (models 1, 2, 3, and 11).

The data are averaged over 15 initial TPQ vectors, and the shaded regions show the standard deviations. We generically observe a two-peak structure, the high-$T$ peak of which appears to be well converged. The lower temperature peak corresponds to magnetic ordering, and may be quite sensitive to finite-size effects, or to the difference in symmetry between the 24- and 32-site clusters.

Modified ab initio model

Having established that the two ab initio models are consistent with the experimental specific heat, we now ask whether they can be modified to better describe the INS data. As discussed in the section on evolution of INS spectra, the large gaps at the zone centers in Fig. 3a, f may be due to overestimated ${\Gamma }_{1}^{^{\prime} }$ or ${J}_{3}$ values. Since ${\Gamma }_{1}^{^{\prime} }$ is sensitive to the degree of trigonal distortion, it can be expected to vary between crystal samples. It is thus likely the parameter with the highest degree of uncertainty. For these reasons, we consider the effect of reducing $| {\Gamma }_{1}^{^{\prime} }|$ in the model of ref. ⁴⁴, while leaving other parameters (${J}_{3}$ included) unchanged. We use bond-averaged interaction parameters.

We again find that the spin wave gap at the $\Gamma$ point depends strongly on the value of ${\Gamma }_{1}^{^{\prime} }$, and that the low-energy features of the INS spectrum can be well explained when $| {\Gamma }_{1}^{^{\prime} }|$ is significantly reduced but still finite. Specifically, we take ${\Gamma }_{1}^{^{\prime} }\to 0.05{\Gamma }_{1}^{^{\prime} }$. (The full parameter set is given in Supplementary Table 2.) The spectrum for this case is shown in Fig. 8a. In this case, we find ${\omega }_{\Gamma }=2.5$ meV, ${\omega }_{{\rm{M}}}=2$ meV, close to the values obtained in ref. ²⁴: ${\omega }_{\Gamma }$ = 2.69 ± 0.11 meV, ${\omega }_{{\rm{M}}}$ = 2.2 ± 0.2 meV. We note that our value for ${\omega }_{\Gamma }$ is consistent with the the low-energy magnon energy of 2.5 meV observed using THz spectroscopy.^40,41 As we noted earlier, the relative intensity of the $\Gamma$ point peak may be enhanced at finite temperature.⁵¹

Fig. 8: The modified ab initio model.

Shown in a is the $I({\bf{q}},\omega )$ spectrum for the modified ab initio model, calculated using ED. We find low-energy peaks at the M and $\Gamma$ points consistent with peaks in experimental INS data. The SSF is shown in the top panel of b, clearly consistent with a zigzag order. The bottom panel of b shows $I({\bf{q}},\omega )$ integrated over [4.5, 7.5] meV, with less intensity at the zone center than is experimentally observed. c shows the magnetic specific heat calculated using TPQ and 15 random initial vectors compared with the experimental data from ref. ³⁴. The shaded region shows the standard deviation. The calculations were all done using the 24-site cluster.

Figure 8b shows the SSF, which remains consistent with zigzag order, and $I({\bf{q}},\omega )$ integrated over the [4.5, 7.5] meV range. From this integrated intensity and Fig. 8a we see that there is a lack of intensity at the zone center within the chosen energy range, unlike the notable star shape in ref. ²³. The source of this discrepancy is not clear, and calls for further study and parameter refinement. Finally, in (c) we show the magnetic specific heat calculated for this modified model. We do find ${T}_{{\rm{h}}}\approx 83$ K, which is higher than the $\approx \!70$ K reported in ref. ³⁴, yet consistent with the broader range of values proposed (70–100 K).

Discussion

We have found that there is a considerable qualitative difference between proposed spin Hamiltonians that describe the INS data well, and realistic models derived using ab initio methods, which are consistent with the reported magnetic specific heat observations. This difference is accompanied by a significant discrepancy in overall energy scales. The specific heat measurements probe the energy density of states, and should represent a good guide to the energy scale, provided the phonon background is handled adequately. In light of our results we thus expect the Kitaev and off-diagonal couplings strengths to be larger, and that $\alpha$-RuCl$_{3}$ may be closer to the QSL regime than previously believed. (We note that recent anisotropic susceptibility⁷⁰ and THz spectroscopy experiments⁴¹ are also consistent with higher Kitaev strengths than in Model 2.) In contrast, the calculated dynamical spin structure factors and INS intensities are much more sensitive to the relative strengths of different interaction terms. They are particularly useful probes for models with fewer degrees of freedom, such as the ${J}_{1}-{K}_{1}-{\Gamma }_{1}-{\Gamma }_{1}^{^{\prime} }-{J}_{3}$ model we study. At the same time, static properties such as magnetic order or SSFs, are clearly insufficient to fully constrain the $\alpha$-RuCl$_{3}$ spin Hamiltonians. In this respect, properties in the presence of magnetic fields, such as phase transitions and the magnon thermal Hall effect,⁵² present a particularly promising direction for both theory and experiment.

By using one of the ab initio models (Eichstaedt et al.⁴⁴) as a starting point and reducing the magnitude of ${\Gamma }_{1}^{^{\prime} }$, we are able to identify a set of parameters (full values are given in Supplementary Table 2) that partly resolve the discrepancy between the two classes of models mentioned above. We find low-energy peaks in the INS spectrum and a high-temperature peak in the magnetic specific heat that are consistent with experiment. However, this should not yet be considered a fully accurate model, as there is an unexplained lack of intensity at the zone center at intermediate frequencies. Instead, we consider it a new starting point.

With these results in mind, we now return to the question we posed in the abstract, about the nature of the correct spin Hamiltonian for $\alpha$-RuCl$_{3}$. From a variety of ab initio and DFT calculations, we expect a minimal model to include ferromagnetic nearest-neighbor Kitaev and Heisenberg couplings, ${\Gamma }_{1}\,>\,0$, a ${\Gamma }_{1}^{^{\prime} }\,<\,0$ term, and a small ${J}_{3}\,>\,0$. Our results for the modified ab initio model further suggest that ${\Gamma }_{1}^{^{\prime} }$ should be small, but finite. Since both ${\Gamma }_{1}^{^{\prime} }$ and ${J}_{3}$ act to stabilize the zigzag order, small values are consistent with the fact that a relatively weak in-plane magnetic field can take $\alpha$-RuCl$_{3}$ out of the ordered phase. Alternatively, $\alpha$-RuCl$_{3}$ might be close to a quantum critical point,^32,33,51 which would be a very exciting scenario. Anisotropic susceptibility measurements⁷⁰ point towards significant off-diagonal ${\Gamma }_{1}$ and ${\Gamma }_{1}^{^{\prime} }$ terms, which may also help stabilize the purported spin liquid phase at finite magnetic fields.^64,71,72 At this point it is not clear whether anisotropies between bonds or the interlayer coupling play a qualitative role, but they are also expected in a full model.

We hope that our results can help guide further theory development and interpretation of experimental results going forward, both for $\alpha$-RuCl$_{3}$ and other Kitaev spin liquid candidate materials. Since we found the INS predictions to be particularly sensitive to small parameter changes, it would be very useful to consider additional modeling techniques and additional observables. For example, machine learning methods may be a promising way to efficiently handle the high-dimensional parameter space. In addition, further experiments in applied magnetic fields can help constrain the Hamiltonian by suppressing fluctuations.

Methods

We use the ${\mathcal{H}}\Phi$⁷³ library for numerical calculations on finite-size systems. We employ a 24-site cluster with ${C}_{3}$ symmetry, and a rhombic 32-site cluster, see Fig. 2. The momenta compatible with the finite-size clusters are shown in Supplementary Note 1. Finite-temperature specific heat is computed using the microcanonical thermal pure quantum state (TPQ) method,^55,63,74 and averaged over ${\ge} \!15$ random initial vectors. The key idea behind the TPQ method is that a quantum system at thermal equilibrium can be reliably described by a single, iteratively constructed state. Utilizing this fact allows for a significant reduction in computational cost compared with finite-temperature exact diagonalization methods.

Zero-temperature properties are calculated using the Lanczos exact diagonalization method, and the continued fraction expansion (CFE)⁵⁴ is used to compute the dynamical quantities. A total of 500 Lanczos steps are used to calculate the CFE. We take 1 meV as a representative value for the experimental energy resolution at full-width/half-maximum,^23,24 and emulate it in the exact diagonalization calculations by using a Lorentzian broadening of 0.5 meV. For the INS spectral evolution calculations we used a Lorentzian broadening of 0.05 in the fixed energy scale. The neutron scattering intensity $I\left({\bf{q}},\omega \right)$ is defined^27,51

$$I\left({\bf{q}},\omega \right)\propto {f}^{2}(q)\sum _{\mu ,\nu }\left[{\delta }_{\mu \nu }-\frac{{q}_{\mu }{q}_{\nu }}{{q}^{2}}\right]{S}^{\mu \nu }\left({\bf{q}},\omega \right),$$

(8)

where $f(q)$ is the magnetic form factor, ${q}^{a}$ is the projection of the momentum vector onto the spin components in the local cubic coordinate system also used for the spin Hamiltonian, and ${S}^{\mu \nu }\left({\bf{q}},\omega \right)$ is the dynamical spin structure factor at momentum ${\bf{q}}$ and frequency $\omega$,

$${S}^{\mu \nu }\left({\bf{q}},\omega \right)=\int \sum _{i,j}\left\langle {S}_{i}^{\mu }\left(t\right){S}_{j}^{\nu }\left(0\right)\right\rangle {{\rm{e}}}^{-i{\bf{q}}\cdot \left({{\bf{r}}}_{i}-{{\bf{r}}}_{j}\right)}{{\rm{e}}}^{-i\omega t}\ {\rm{d}}t$$

(9)

Note that the off-diagonal elements of ${S}^{\mu \nu }\left({\bf{q}},\omega \right)$ contribute significantly for most models studied here, due to the presence of ${\Gamma }_{1}$ and ${\Gamma }_{1}^{^{\prime} }$ interactions. The static spin structure factor, $S\left({\bf{q}}\right)=\int S\,\left({\bf{q}},\omega \right)\ {\rm{d}}\omega$, is evaluated separately. We note that neutron scattering experiments probe the magnetization ${\bf{M}}$, while the Hamiltonians in Eqs. (1) and (2) are expressed in terms of the pseudospin ${\bf{S}}$. Hence the form of Eq. (9) amounts to an assumption that ${\bf{M}}$ and ${\bf{S}}$ are approximately parallel. However, trigonal distortion can induce an angle between the two vectors, and a resulting $g$-factor anisotropy.⁷⁵ While there have been conflicting reports about the degree of anisotropy,^48,68,76 a more recent X-ray absorption spectroscopy study⁷⁷ found $\alpha$-RuCl$_{3}$ to have only weak trigonal distortion and a nearly isotropic $g$-factor. In light of this result and the relatively weak ${\Gamma }_{1}^{^{\prime} }$ interactions in Table 1 we assume that ${\bf{M}}$ and ${\bf{S}}$ are indeed approximately parallel in $\alpha$-RuCl$_{3}$.

$f(q)$ is assumed to be isotropic, which is justified for small scattering wave numbers.²³ The magnetic form factor for Ru$^{3+}$ was calculated using DFT in the Supplementary Material of ref. ²⁵. By fitting their data to a Gaussian we have obtained the analytical approximation

$$f(q)=\exp \left(-\frac{{q}^{2}}{{\left(2\pi * 0.25\right)}^{2}}\right).$$

(10)

We integrate over the momentum direction perpendicular to the honeycomb plane, following the experiment.²³ Since the ED calculation is necessarily two-dimensional we assume that ${S}^{\mu \nu }\left({\bf{q}},\omega \right)$ is constant along the perpendicular direction during the integration step. We expect this to be a reasonable approximation due to the strong two-dimensionality of $\alpha$-RuCl$_{3}$,⁷⁸ and the relatively small interlayer coupling.³²