Abstract
Selectively modulating the sublattices in 3D transition metal oxides via strains could tailor the electronic configurations with emerging anomalous properties, which provides new platforms for fundamental researches as well as designs of devices. Here, we report tailoring the oxygen octahedral sublattices in vanadium dioxide (VO2) thin films by anisotropic in-plane strains, and the observation of in-plane orientation-dependent metal–insulator transition. Through multimodal characterizations based on high-resolution X-ray diffraction, electrical transport measurements, and polarization-dependent X-ray absorption spectroscopy at different temperatures, we demonstrate that nonequal strains were successfully induced along A and B oxygen octahedral chains in VO2 films via a special design of epitaxial growth on vicinal substrates. The V 3d1 orbital configurations are modulated in the two oxygen octahedral chains, resulting in in-plane orientation-dependent metal–insulator transition behaviors such as reduced hysteresis width and anisotropic phase transition temperature. This work provides new fundamental insights on metal–insulator transitions, and more importantly, opens up new opportunities for material and device developments
Similar content being viewed by others
Introduction
Exploring exotic physical properties in 3D transition metal oxide films by using epitaxial elastic strains is a popular way in materials science.1,2 Strain, as a tool of modifying the crystal lattice of the oxide films, can simultaneously modify the interaction between charge, orbital and spin degrees of freedom, which are strongly related to the physical properties of materials.2,3,4,5 For some 3D transition metal oxides, sublattices with different spatial symmetries often coexist in their crystal lattices, such as in Fe3O4, CoFe2O4, Vanadium dioxide (VO2), and some superconductor cuprates crystal lattices.3,6,7 These sublattices, including oxygen octahedral, oxygen tetrahedron, and oxygen dodecahedron, are fundamental functional unit cells of oxides. Although strain engineering techniques have been developed for decades,8 controllably manipulating the sublattices of the 3D transition metal oxides still needs deep and systematical investigations. Especially, knowledge on correlation between the spatial symmetries of the sublattice unit cells and the symmetries of the charge, orbital and spin degrees of freedom of the 3D electrons inhabited in them, can provide a knob to tailor the sublattice of the 3D transition metal oxides using strain and thus to explore novel physical properties for practical applications.
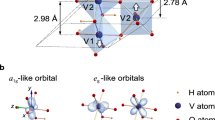
VO2, a classical strong-correlated oxide that has a sharp metal–insulator transition (MIT) near 341 K, is a typical 3D transition metal oxide consisting of two types of sublattices, i.e., two types of edge-shared oxygen octahedral chains.2,3,9,10 The MIT properties of VO2 mainly originate from the V–V dimers inhabited in these two distinguishable edge-shared oxygen octahedral sublattices, which are called A octahedral chain and B octahedral chain. The A octahedral chain and the B octahedral chain are arranged alternatively with a relative 90° rotation around cR axial, as seen in Fig. 1a, b (a simplify structure depicture can be accessed in Fig. S1). During the MIT, VO2 transfers from a rutile structure into a monoclinic structure, meanwhile the V ions shift and form the V–V dimers.2,3,9,10 More exact to say, there is a shifting component along the VO2[001]R direction for both V ions of the A octahedral chain and the B octahedral chain. Besides, they have different shifting components in the VO2 (001)R lattice plane. As shown in Fig. 1b, V ions of A octahedral chain shift along VO2 \([1\bar 10]_{\mathrm{R}}\) direction, while V ions of B octahedral chain shift along VO2 [110]R direction. Obviously, the deformation along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions would strongly impact the shifting components of V ions. Since the MIT properties of VO2 have been demonstrated very sensitive to the strains along the V–O bond,3,10 it is believed that the strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions would be one of the key factors affecting the MIT properties of VO2.
The schematic of lattice and electronic structures for VO2: a the VO2 lattice constructed with A and B oxygen octahedral chains which are edge-shared oxygen octahedral chains with V ions located inside the oxygen octahedral; b the details of A and B octahedral chains of VO2; c the definition of V–O apical bonds and equatorial bonds of oxygen octahedral in VO2; d the lattice of VO2 grown on a normal TiO2 (001) substrate, which undergoes symmetric biaxial strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions; e the lattice of VO2 grown on a vicinal TiO2 (001) substrate with asymmetric biaxial strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions, in which the VO2 [110]R direction is the vicinal direction and bares a smaller strain compared with VO2 \([1\bar 10]_{\mathrm{R}}\) direction; (f–h) the schematic of the dxy, dxz, and dyz molecular orbitals of VO2 observed from VO2 [001]R direction, respectively
The strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions can tailor the apical V–O bond length (defined in Fig. 1c) of VO2, which influences the overlap of V 3d and oxygen 2p orbitals, hence changes the electronic configuration of VO2 and its MIT properties.2,3 The V ions inhabit in the center of oxygen–octahedral cage and the crystal field of the oxygen octahedral splits the 3d orbital into twofold degenerate eg orbitals and triple fold degenerate t2g orbitals. The eg orbitals contain \({d}_{{\mathrm{x}}^2 + y^2}\) and \({d}_{{\mathrm{z}}^2}\) which directly point toward the oxygen ions, hence lifting up their energy levels relative to the t2g orbitals. In this case, the V d1 electron would occupy the t2g orbital rather than the eg orbital.5 For the t2g orbitals (dxy, dxz, and dyz), the structural distortion of VO2 further splits the orbitals into d∥ (dxy) and π* (dxz and dyz).2,4 The V 3d1 electron occupies d∥ orbital in the insulating state of VO2. However, in the metallic VO2, the electrons normally redistribute and occupy both the d∥ and π* orbitals (as shown in Fig. S2). The redistribution of V 3D electrons is very sensitive to the energy levels of d∥ and π* orbitals, which are strongly influenced by the apical V–O bond length.3 If we observe along the cR direction, the dxy, dxz, and dyz orbitals extend to different directions in VO2(001)R plane (as shown in Fig. 1f–h).4,5 The A octahedral chain and the B octahedral chain have a relative 90° rotation around cR axis, so their apical V–O bond and orbitals also rotate. Since the energy level of π* is sensitive to the apical V–O bond length, the energy levels of π* of 3d1 electrons in A octahedral chain and the B octahedral chain would be influenced by strains with a relative 90° rotation, respectively. When isotropic biaxial strains are loaded along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions(as the case of Fig. 1d), the apical V–O bond lengths of both the A octahedral chain and the B octahedral chain would be tuned to the same degree simultaneously, as reported by Aetukuri et.al.3 The isotropic biaxial strains loaded along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions can modulate the electronic configurations of V 3D electrons, consequently significantly tune the MIT temperature. Since the strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions can selectively influence the apical V–O bond lengths of the A octahedral chain and the B octahedral chain, their sublattices could be tuned separately with nonequal strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions. In other words, the orbital configurations of the A octahedral chain and the B octahedral chain can be tailored separately by the anisotropic strains(as the case of Fig. 1e). High-quality works on tailoring the MIT properties of VO2 in virtue of thickness effects on the epitaxial strain,11,12 thermal strain,13 and interface facet effect14 were reported. However, researches on the effect of anisotropic strains are still rare. Although the experiments of loading uniaxial strain along the [110]R direction have been demonstrated in VO2 nanowire system,10,15 the impact of the applied strain on the physical properties was hardly determined due to the dimension limitation. Furthermore, there is few data available on the anisotropic electron transport properties and the electronic configurations under the anisotropic strains. On the other hand, it has been demonstrated that substrates with small miscutting angles can induce designable strains in the films by virtue of the mismatching between the surface–step–terrace of the substrate and lattice unit cells of the films.16,17,18,19 For the substrates with miscutting angles, the surface–step–terrace can be formed after being annealed at a high temperature and its width can be adjusted by tuning the miscutting angles. When the films are grown on such substrates, the lattice unit cells of the films have to accommodate the width of surface–step–terrace, consequently strain is induced. (more details can be accessed in Supplementary Figs. S3 and S4). Herein, we induce nonequal strains in a VO2 film via high-quality epitaxial growth on a designed vicinal TiO2 (001) substrate with a small miscutting angle along VO2 [110]R direction and directly observe an in-plane orientation-dependent MIT behavior of the as-grown VO2 film.
It is found that by high-quality epitaxial growth through sophisticated experimental control, anisotropic biaxial in-plane strains are induced in A and B oxygen octahedral chains in the VO2 film, resulting in an in-plane orientation-dependent MIT in VO2 film, e.g., obvious anisotropy in conductivity, crystal-orientation dependency of phase transition temperature Tc, and reduction of phase transition hysteresis width.
Results
The VO2 films were grown using a polymer-assisted deposition technique.20 More details can be accessed in our previous reports.21,22 The epitaxial relationship between the films and the substrates is VO2 (001)R ∥ TiO2(001) and VO2 [110]R ∥ TiO2[110] (Supplementary Fig. S5). And the thickness of the films is about 17 nm. An ordinary TiO2 (001) substrate with no intentional miscut and a vicinal TiO2 (001) substrate with a 1° miscutting angle along TiO2 [110] direction were used for comparative study. The anisotropic in-plane strains were successfully induced in the VO2 film on the vicinal TiO2(001) substrate as manifested by the high-resolution reciprocal space mapping (RSM) (Fig. 2). For the film grown on the normal TiO2 (001) substrate, equal strain of σa was found along both VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions in the VO2 film (Fig. 1d). However, the case was found to be different for the VO2 film grown on the vicinal TiO2 (001) substrate. We denoted the strain in the film grown on the vicinal substrate along the VO2 [110]R direction as \(\sigma {\prime}_{\mathrm{a}}\) and along the VO2 \([1\bar 10]_{\mathrm{R}}\) direction as σb (Fig. 1e). It was found that the strain \(\sigma {\prime}_{\mathrm{a}}\) is very close to σa but the strain σb is different from the strain σa. Obviously, the strain along the VO2 [110]R direction was modulated by the surface–step–terraces on the vicinal substrate, as what it can be expected.
Figure 2 show the RSMs for the nonvicinal and vicinal samples in both the metallic and insulating states, measured at 298 and 373 K, respectively. Lattice parameters of the VO2 thin films are calculated based on the RSM data and listed in Table 1. It is clearly indicated that the anisotropic in-plane biaxial strains (\(\sigma^ {\prime}_{\mathrm{a}}\) and σb) have been induced along [110]R and \([1\bar 10]_{\mathrm{R}}\) directions in the VO2 film on the vicinal substrate. The most profound influence of the anisotropic in-plane strains on the VO2 lattice is the ability of tailoring the apical V–O bond length of the sublattices in the different octahedral chains separately. The A octahedral chain bares the σa' strain while the B octahedral chain bares the σb strain along the apical V–O bond direction. The anisotropic in-plane biaxial strains will result in different apical V–O bond lengths in the A and B octahedral chains. From the measured lattice parameter in Table 1, we can estimate the apical V–O bond lengths for both samples in the metallic states. For the nonvicinal sample, obviously, the apical V–O bond lengths can be considered as the same for both A octahedral chain and B octahedral chain, which are determined to be 1.9331 Å in the metallic state. However, for the vicinal sample, they become 1.9538 Å and 1.9208 Å for the A octahedral chain and the B octahedral chain in the metallic state, respectively. The nonequal apical V–O bonds in the A octahedral chain and the B octahedral chain for the vicinal sample are resulted from the nonequal biaxial strains.
The change of the apical V–O bond length by strain would affect the overlap of V 3d and O 2p orbitals. A shorter apical V–O bond length increases the overlap of V 3d and O 2p orbitals, which would increase the energy level of π* orbitals relative to those of the d∥ orbitals, hence decrease the electron occupancy of π* orbitals. Since the d∥ and π* orbitals are both partially occupied in the metallic state, as shown in Fig. S2, the electron occupancy of d∥ orbitals will increase correspondingly.3 In other words, the nonequal strains in the VO2 film along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions result in nonequal apical V–O bond lengths in A and B octahedral chains, leading to different energy levels of π* orbitals and different electronic configurations of the A and B octahedral chains.
To verify the electronic state configurations described above, synchrotron-based linear-polarization-dependent X-ray absorption spectroscopy (XAS) was tested at the V L2,3 edges of both VO2 thin films epitaxially grown on non-vicinal and vicinal substrates. The experiments were performed using total electron yield (TEY) detection with a typical probe depth of about 10 nm. Linearly polarized X-rays with the electric-field orientation parallel (E ⊥ cR) and perpendicular (E ⊥ cR) to the rutile VO2 c-axis are measured to probe the vacant d∥ and π* valence-electron states, respectively.3 To investigate the anisotropic in-plane strain effect, the measurements perpendicular to the rutile c-axis (E ⊥ cR) were performed along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions, respectively. Based on previous studies on the valence-electron states,3 we particularly focus on the excitonic features of the XAS spectra with 512–516 eV photon energies.
Figure 3 shows the polarization-dependent V L-edge XAS spectra in the metallic and insulating states of the nonvicinal and vicinal samples. The intensity differences I∥ − I⊥, which are respectively defined as \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) and \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\) along the VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions, are also plotted. In the insulating state, the dichroic signals \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) and \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\) (Fig. 3a, b) of both nonvicinal and vicinal samples show negligible difference. That is expected and consistent with the previous report,3 because the 3d1 electron occupies the d∥ orbitals while the π* orbitals located above the Fermi level are empty in the insulating state. However, the orbital occupancy in the metallic state, which is believed to set the energy scale for the MIT of VO2,3 shows remarkable distinctions between the two samples, as reflected by the XAS data. It is found that the XAS dichroic signals, \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) and \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\), of the nonvicinal sample in the energy region of 512–516 eV show negligible difference in the metallic state (Fig. 3c), which is as expected due to the equal strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions. On the other hand, the XAS dichroic signals \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) and \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\) of the vicinal sample in the metallic state (Fig. 3d), show obvious difference in this energy region, which should be attributed to the nonequal strains along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions. For the vicinal sample, the apical V–O bond length of the B octahedral chain (1.9208 Å) was shorter than the A octahedral chain (1.9538 Å), suggesting that the difference in the XAS dichroic signals \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) and \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\) is due to the redistribution of the orbital occupation. As mentioned ahead, the shorter apical V–O bond length increases the p–d overlap, hence raises the energy level of π* orbital and consequently reduces their orbital occupancy, resulting in the increase of the orbital occupancy of d∥ orbitals. Since the XAS data correspond to the unoccupied states of the orbitals, the increase of the occupancy of d∥ orbitals will reduce the signal \(I_{{\mathrm{C}}_{\mathrm{R}}}\). For the π* orbitals, the dyz orbitals extend to [100]R and [010]R directions (Fig. 1h). Thus, the related XAS signals display no difference with the X-ray electric field along either [110]R or \([1\bar 10]_{\mathrm{R}}\) directions. However, the dxz orbitals of B octahedral chain extend along [110]R direction (Fig. 1g) while the dxz orbitals of A octahedral chain extend along \([1\bar 10]_{\mathrm{R}}\) direction. The anisotropic in-plane strain effect, i.e., a shorter lattice parameter along the [110]R, would increase the energy level and decrease the orbital occupancy of the dxz orbitals in the B octahedral chain, compared with those in the A octahedral chain. Such an effect is directly shown in the XAS raw data plot in Fig. 3d, with stronger \(I_{[110]_{\mathrm{R}}}\) signals comparing with \(I_{[1\bar 10]_{\mathrm{R}}}\), leading to smaller \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[110]}\) than \(I_{{\mathrm{C}}_{\mathrm{R}}} - I_{[1\bar 10]}\). Therefore, the XAS data in the metallic states clearly prove that the anisotropic in-plane strains have effectively changed the orbital occupancy of the two sublattices.
Since the nonequal apical V–O bonds of the A octahedral chain and the B octahedral chain change the electronic configurations of the VO2 film on the vicinal substrate, it can significantly modulate the MIT behaviors of the film. Temperature-dependent resistances of both the nonvicinal and the vicinal samples were tested. In-plane orientation-dependent MIT behavior attributed to the anisotropic in-plane strains were observed in the vicinal sample.
The nonvicinal sample exhibits a normal MIT behavior (Fig. 4a, c). The resistance-temperature (R − T) curves tested along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions show weak directional dependency, as shown in the direction-dependent resistance in metallic state is shown in Fig. 4e. Its phase transition temperature (Tc) for heating was determined to be 324 K in both VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions (derived from the dlnR/dT-T curves in Fig. 4c), and the hysteresis width (ΔTc, defined as the difference of Tc for heating and cooling) is about 3.5 K. These results are very similar to previous reports.23,24 However, for the vicinal sample, the MIT behavior has been obviously altered (Fig. 4b, d).The R − T curves tested along VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions show obvious directional dependency. The film in the metallic state has a much larger resistance along the VO2 [110]R direction (vicinal direction) than that along the VO2 \([1\bar 10]_{\mathrm{R}}\) direction. The direction-dependent resistance in metallic state is shown in Fig. 4f, which can be fitted by:
where \(R_{[110]_{\mathrm{R}}}/R_{[1\bar 10]_{\mathrm{R}}} = 17.3\). The phase transition temperature exhibits anisotropy as well. The Tc values measured along [110]R and \([1\bar 10]_{\mathrm{R}}\) directions are determined to be 333 and 326 K, respectively. From Table 1, we observe that the vicinal sample undergoes a tensile strain along the \([1\bar 10]_{\mathrm{R}}\) direction, while it undergoes a compressive strain along the [110]R direction. The higher value of Tc along the [110]R direction should be attributed to the compressive strain along that direction.
The electrical properties. a Temperature-dependent resistance and c dlnR/dT-T curves of the nonvicinal sample, respectively; b temperature-dependent resistance and d dlnR/dT-T curves of the vicinal sample, respectively; e, f the experimental and fitting results of direction-dependent resistance for the nonvicinal and vicinal sample in metallic state, respectively
Discussion
A possible mechanism for the conductivity anisotropy is the strip-like phase domain structure generated by the phase separation during the phase transition in the film.25 Clearly, mixture of the metallic and insulating phases would occur in the temperature range near the phase transition temperature. This mixing phase domains would form anisotropic percolation hence lead to anisotropic carrier transport behavior. Anisotropy of the conductivity induced by this mechanism will disappear beyond the phase transition temperature range, since the phase transition has completed and the metallic and insulating domains no longer coexist. However, our vicinal sample shows obvious anisotropic conductivity even at a high (373 K) and a low (298 K) temperature beyond the phase transition temperature. Other mechanisms need to be proposed to understand the phenomenon. We suggest that the anisotropic in-plane strains play a key role. The shorter apical V–O bond in the B octahedral chain compared with the A octahedral chain increases the p–d overlap and the dxz energy level. Since the dyz orbitals of the B octahedral chain extend to [110]R direction while those of the A octahedral chain extend to \([1\bar 10]_{\mathrm{R}}\) direction, if we assume that the d∥ orbital levels are the same in the A and B octahedral chains, the electron hopping would be harder along [110]R than \([1\bar 10]_{\mathrm{R}}\). As a result, the resistance along [110]R is larger than that along \([1\bar 10]_{\mathrm{R}}\).
Moreover, the nonequal apical V–O bonds change the electronic configurations of the A octahedral chain and the B octahedral chain, leading to different energy scales for the MIT along \([1\bar 10]_{\mathrm{R}}\) and [110]R directions. Since the apical V–O bond length expands when VO2 transfers from a low temperature monoclinic phase to a rutile phase, a longer apical V–O bond length would make the phase transition easier, therefore yielding a lower transition Tc along \([1\bar 10]_{\mathrm{R}}\) than [110]R.
An anomalous change in the phase transition hysteresis width was also observed in the vicinal sample. As shown in Fig. 4, the hysteresis width ΔTc almost disappeared in the vicinal sample, i.e, the values of ΔTc are as small as 0.2 K along both VO2 [110]R and \([1\bar 10]_{\mathrm{R}}\) directions, which are much smaller than that of the nonvicinal sample (ΔTc = 3.5 K). The reason for the dramatically reduced hysteresis width ΔTc is not clear yet. It may be related to the modification of the shearing strain in the VO2 film during the MIT. In the previous reports,26,27 the hysteresis width can be expressed as:
where η is the domain shape parameter, G is the shear modulus, γ is the shearing strain, and ΔS is entropy change of the phase transition. The asymmetrical in-plane strains in the film may alter the shearing strain γ hence narrow the hysteresis loop.
By epitaxial growth of a high-quality VO2 thin film on a designed vicinal TiO2 substrate, we deliberately tailored the sublattices of VO2 crystal utilizing the nonequal biaxial in-plane strains. The anisotropic in-plane strain leads to different apical V–O bond lengths in A and B octahedral chains of the VO2, which modulates the orbital configurations of V 3d1 and induces in-plane orientation-dependent MIT behaviors in the VO2 film. Specifically, direction-dependent conductivity and phase transition temperature Tc, as well as the significant reduction of the hysteresis width ΔTc, have been observed. Our experimental results demonstrate the feasibility of tailoring the sublattices in the 3D transition metal oxides for modulating their electronic configure using anisotropic strains. This demonstration presents a unique platform in the material genetic design for exploring both fundamental physical properties and practical applications.
Methods
The vicinal TiO2 (001) substrate and the normal TiO2 (001) substrate were both ultrasonically cleaned in acetone and deionized water, then immersed in 5 vol% HCl solution for 5 min to remove the metal contamination on the surfaces of the substrates before being washed in deionized water. After that, the substrates were etched in 20 vol% HF solution for 2 min, and then ultrasonically cleaned in deionized water. Finally, the substrates were annealed in oxygen at 750 °C for 2 h to form a surface with clear step–terrace structures. The high-resolution reciprocal space maps were tested using PANalytical XPert MRD. The temperature dependence of resistance of the films was measured using an Agilent B2900A source meter with the four-point probes method in a high-vacuum system. The anisotropic resistance of the VO2 films was also measured with the four-point probes method by rotating the samples. The temperature-dependent polarization-dependent XAS was carried out with >99% linearly polarized X-ray beam, which was carefully aligned onto the samples mounted on an in-vacuum rotating goniometer with temperature controls. Sample current was collected as the TEY signals upon incident photons. The XAS spectra shown here have been normalized to the photon flux that was monitored by the photocurrent of a clean gold mesh simultaneously. Experimental resolution is better than 0.16 eV at V–L edges, not considering core-hole broadening.
Data availability
All data supporting the findings of this study are available from the corresponding authors Y.L. and M.G. upon request.
References
Schlom, D. G. et al. Elastic strain engineering of ferroic oxides. MRS Bull. 39, 118–130 (2014).
Aetukuri, N. B. et al. Control of the metal–insulator transition in vanadium dioxide by modifying orbital occupancy. Nat. Phys. 9, 661–666 (2013).
Eyert, V. The metal-insulator transitions of VO2: a band theoretical approach. Ann. Phys. 11, 650–704 (2010).
Morrison, V. R. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Haverkort, M. W. et al. Orbital-assisted metal-insulator transition in VO2. Phys. Rev. Lett. 95, 196404 (2005).
Mcqueeney, R. J. et al. Zener double exchange from local valence fluctuations in magnetite. Phys. Rev. Lett. 99, 246401 (2007).
Fritsch, D. & Ederer, C. First-principles calculation of magnetoelastic coefficients and magnetostriction in the spinel ferrites CoFe2O4 and NiFe2O4. Phys. Rev. B 86, 41–48 (2012).
Lin, Y. & Chen, C. L. Interface effects on highly epitaxial ferroelectric thin films. J. Mater. Sci. 44, 5274–5287 (2009).
Goodenough, J. B. The two components of the crystallographic transition in VO2. J. Solid State Chem. 3, 490–500 (2015).
Park, J. H. et al. Measurement of a solid-state triple point at the metal–insulator transition in VO2. Nature 500, 431–434 (2013).
Théry, V., Boulle, A., Crunteanu, A. & Orlianges, J. Combined strain and composition-induced effects in the metal-insulator transition of epitaxial VO2 films. Appl. Phys. Lett. 111, 251902 (2017).
Yang, Y. et al. Thickness effects on the epitaxial strain states and phase transformations in (001)-VO2/TiO2 thin films. J. Appl. Phys. 125, 082508 (2019).
Théry, V. et al. Role of thermal strain in the metal-insulator and structural phase transition of epitaxial VO2 films. Phys. Rev. B 93, 184106 (2016).
Corder, S. N. G. et al. Controlling phase separation in vanadium dioxide thin films via substrate engineering. Phys. Rev. B 96, 161110 (2017).
Wei, J., Wang, Z., Chen, W. & Cobden, D. New aspects of the metal-insulator transition in vanadium dioxide nanobeams. Nat. Nanotechnol. 4, 420–424 (2009).
Sánchez, F., Ocal, C. & Fontcuberta, J. Tailored surfaces of perovskite oxide substrates for conducted growth of thin films. Chem. Soc. Rev. 43, 2272–2285 (2014).
Perna, P. et al. Engineering large anisotropic magnetoresistance in La0.7Sr0.3MnO3 films at room temperature. Adv. Funct. Mater. 27, 1700664 (2017).
Lu, H. et al. Surface-step-terrace-induced anomalous transport properties in highly epitaxial La0.67Ca0.33MnO3 thin films. ACS Appl. Mater. Interfaces 2, 2496–2499 (2010).
Zou, Q. et al. Step terrace tuned anisotropic transport properties of highly epitaxial LaBaCo2O5.5+δ thin films on vicinal SrTiO3 substrates. ACS Appl. Mater. Interfaces 6, 6704–6708 (2014).
Jia, Q. X. et al. Polymer-assisted deposition of metal-oxide films. Nat. Mater. 3, 529–532 (2004).
Ji, Y. D. et al. Epitaxial growth and metal-insulator transition of vanadium oxide thin films with controllable phases. Appl. Phys. Lett. 101, 071902 (2012).
Ji, Y. et al. Role of microstructures on the m1-m2 phase transition in epitaxial VO2 thin films. Sci. Rep. 4, 4854 (2014).
Bayati, M. R. et al. Correlation between structure and semiconductor-to-metal transition characteristics of VO2/TiO2/sapphire thin film heterostructures. Acta Mater. 61, 7805–7815 (2013).
Li, D. et al. Joule heating-induced metal-insulator transition in epitaxial VO2/TiO2 devices. ACS Appl. Mater. Interfaces 8, 12908–12914 (2016).
Liu, M. K. et al. Anisotropic electronic state via spontaneous phase separation in strained vanadium dioxide films. Phys. Rev. Lett. 111, 096602 (2013).
Thompson, Z. J. et al. Terahertz-triggered phase transition and hysteresis narrowing in a nanoantenna patterned vanadium dioxide film. Nano Lett. 15, 5893–5898 (2015).
Gu, Y., Cao, J., Wu, J. & Chen, L. Q. Thermodynamics of strained vanadium dioxide single crystals. J. Appl. Phys. 108, 083517 (2010).
Acknowledgements
This work has been supported by the National Basic Research Program of China (973 Program) under Grant no. 2015CB351905 and the Natural Science Foundation of China (Nos. 61825102, 51872038 and 51602152).
Author information
Authors and Affiliations
Contributions
Y.L., C.C. and W.L. discussed and initiated the study and Y.L. supervised the project. W.L. conducted the fabrication experiments. Z.Z. conducted the XAS measurements. Y.J. and H.Y. performed the RSM measurements. C.L. and M.G. performed the electric measurement. W.L., Z.Z., Y.J., H.Y., M.G., C.C., F.P., and Y.L. analyzed the data and cowrote the manuscript. All authors reviewed and finalized the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liang, W., Zhuo, Z., Ji, Y. et al. In-plane orientation-dependent metal-insulator transition in vanadium dioxide induced by sublattice strain engineering. npj Quantum Mater. 4, 39 (2019). https://doi.org/10.1038/s41535-019-0176-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0176-x