Abstract
Magnetism is widely considered to be a key ingredient of unconventional superconductivity. In contrast to cuprate high-temperature superconductors, antiferromagnetism in most Fe-based superconductors (FeSCs) is characterized by a pair of magnetic propagation vectors, (π,0) and (0,π). Consequently, three different types of magnetic order are possible. Of these, only stripe-type spin-density wave (SSDW) and spin-charge-density wave (SCDW) orders have been observed. A realization of the proposed spin-vortex crystal (SVC) order is noticeably absent. We report a magnetic phase consistent with the hedgehog variation of SVC order in Ni-doped and Co-doped CaKFe4As4 based on thermodynamic, transport, structural and local magnetic probes combined with symmetry analysis. The exotic SVC phase is stabilized by the reduced symmetry of the CaKFe4As4 structure. Our results suggest that the possible magnetic ground states in FeSCs have very similar energies, providing an enlarged configuration space for magnetic fluctuations to promote high-temperature superconductivity.
Similar content being viewed by others
Introduction
The many families of Fe-based superconductors (FeSCs) provide a diverse platform for investigating the fundamental nature and applications of high-temperature superconductivity.1,2 In these compounds, magnetic order and superconductivity seem intertwined and the ground-state can be tuned by pressure and doping. The FeSCs share a common chemical motif; stacked Fe-pnictide or chalcogenide layers. Magnetism in most FeSCs [e.g., all AeFe2As2 (Ae = Ca, Sr, Ba)] is characterized by antiferromagnetic correlations with two symmetry-equivalent propagation vectors, Q 1 = (π, 0) and Q 2 = (0, π) (using the single-iron Brillouin zone notation).1,3 Magnetic order with these propagation vectors can be described by the spatial variation of the iron magnetic moments at positions R (refs. 4,5,6,7,8,9,10,11,12,13),
Three types of magnetic order (Fig. 1a–d) are defined by the relationship between the magnetic order parameters M 1 and M 2 (refs. 3,14,15). The orthorhombic stripe-type spin-density wave (SSDW) order (Fig. 1a) has only one nonzero M i . A spin-charge-density wave (SCDW) (Fig. 1b) is a superposition of the two contributions with M 1 = ±M 2 . Finally, tetragonal spin-vortex crystal (SVC) orders (Fig. 1c, d) are defined by \(\left| {{\boldsymbol{M}}_{\bf{1}}} \right|\) = \(\left| {{\boldsymbol{M}}_{\bf{2}}} \right|\) with non-collinear vectors M 1 ⊥ M 2 , both in the Fe-plane.
Schematics of possible magnetic order types in CaKFe4As4. a–d Sketches of four magnetic moment patterns on an Fe–As layer in the CaKFe4As4 structure associated with Q 1 = (π, 0), Q 2 = (0, π) magnetic propagation vectors. The upper yellow square in a, e represents the projection of the CaKFe4As4 unit cell. The magnetic unit cells are represented by the central yellow squares in a–d. The brown arrows represent the magnetic moments at the Fe sites and the blue and green arrows the hyperfine field (Hhf) at the inequivalent As1 and As2 sites. In the orthorhombic stripe spin-density wave (SSDW) in a all arsenic atoms experience Hhf normal to the plane. In the spin-charge-density wave (SCDW), “C4 phase15”, in b every other Fe site supports a moment normal to the plane and the As sites experience an in-plane Hhf. In the hedgehog spin-vortex crystal (SVC) phase in c, the Fe moments display an “all in” or “all out” arrangement centered around the As1 sites generating an out-of-plane Hhf ≠ 0 at these sites and Hhf = 0 at the As2 sites. In the loops SVC in d the magnetic moments form loops around As1 and neither As site experiences a Hhf. e The chemical structure of CaKFe4As4. Note the inequivalent As1 and As2 sites adjacent to K and Ca planes, respectively. f Section of the Fe–As sheet with a hedgehog SVC moment arrangement. Spin up currents between the iron atoms, Js (yellow arrows), generate an electric field, E (red arrows), which couples to asymmetric shifts of the two arsenic sites. Unlike in the CaFe2As2 structure, an asymmetric arrangement of arsenic atoms is imposed by the crystallographic symmetry in CaKFe4As4 providing a symmetry-breaking field that favors the SVC-type phases
The existence of two vector order parameters, M 1 and M 2 , potentially provides a large configuration space for magnetic fluctuations. They are maximized when different types of magnetic order are close in energy, which may be key to the high-temperature superconductivity in the FeSCs. This makes FeSCs exceptional, as most unconventional superconductors support only a single magnetic order parameter. Although the majority of iron-based superconductors exhibit only SSDW magnetic order, several hole-doped AeFe2As2 (Ae = Ca, Sr, Ba) compounds demonstrate a transition from SSDW to SCDW for compositions near optimal superconductivity.14,15,16,17,18 An experimental realization of SVC order would demonstrate the diversity of magnetic ground-states in FeSCs, but has not been reported to date.
Application of a suitable symmetry-breaking field may coax the system to condense into one of the three types of magnetic order as they break distinct symmetries.12 For example, in-plane uniaxial strain favors SSDW as it breaks tetragonal symmetry in the same way and has been widely employed to study this order.19,20 It is difficult to imagine appropriate, externally applicable, symmetry-breaking fields for SCDW or SVC orders. A SVC phase breaks the glide symmetry across the Fe planes,12 which is present in most FeSCs. Consequently, breaking this glide symmetry could favor SVC order.13 In the recently discovered stoichiometric AeAFe4As4 (Ae = Ca, Sr; A = K, Rb, Cs) superconductors,21 the alternating Ae and A atom planes inherently break this glide symmetry resulting in two inequivalent As sites (Fig. 1e). Consequently, these compounds could provide a unique opportunity to realize and study a SVC phase. Unfortunately, the parent AeAFe4As4 compounds do not order magnetically.21,22 However, recent nuclear magnetic resonance23 and inelastic neutron scattering24 on CaKFe4As4 revealed magnetic fluctuations near the (π, 0), (0, π) Q-vectors. Electron count and experimental properties suggests that CaKFe4As4 can be considered analogous to (Ba0.5K0.5)Fe2As2 (ref.22). In the latter compound, the SSDW is suppressed by hole doping1 (substituting K into BaFe2As2). Inspired by this analogy,25 magnetic order could be induced by electron doping CaKFe4As4. Here, we report that adding electrons via substitution of Co or Ni for Fe in CaKFe4As4 does induce antiferromagnetism consistent with the hedgehog variation of SVC. We stabilize this phase using the chemical structure as a symmetry-breaking field illustrating the multiple competing, nearly-degenerate magnetic phases in FeSCs. This competition may be an important contributor to high-temperature superconductivity as enhanced magnetic fluctuations can boost pairing.
Results
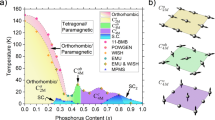
Figure 2a presents the electrical resistance of CaK(Fe1 − xNi x )4As4. With increasing nickel content, a kink at temperature TN appears and rises to ~55 K as the superconducting critical temperature, Tc, is suppressed. The resistance of CaK(Fe1 − yCo y )4As4 (Fig. 2b) exhibits a similar trend. The heat capacity of CaK(Fe0.951Ni0.049)4As4 (insets into Fig. 2a) reveals clear signatures of second-order phase transitions at TN and Tc. The transition temperatures inferred from these data are plotted in Fig. 3, demonstrating that the phase diagrams of Co-doped and Ni-doped CaKFe4As4 map onto each other if the Ni fraction is scaled by two. This is consistent with an electron doping picture where substituting Ni for Fe supplies twice as many electrons as Co (ref. 26). It should be noted that a recent study of RbEuFe4As4 also shows a new phase stabilized by Ni-substitution suggested to be a spin-density wave phase.27
Resistance, magnetic susceptibility, and heat capacity of Co-doped and Ni-doped CaKFe4As4. a Temperature dependence of normalized resistance, R/R300K, of CaK(Fe1 − xNi x )4As4 single crystals demonstrating the suppression of the superconducting transition temperature, Tc, and the emergence of a kink-like feature labeled TN with increasing Ni content, x. The anomaly at TN appears clearly as a step in the derivative of resistance, dR/dT, and specific-heat, Cp, of x = 0.049 (upper left insets). In the magnified portion in the specific-heat inset, data from a x = 0.017 sample was subtracted to accentuate the step-like anomaly characteristic of a bulk, second-order transition at TN. The zero-field cooled (ZFC) volume magnetic susceptibility, 4πχ, (bottom right inset) demonstrates the suppression of Tc with increasing x and full superconducting shielding for x ≤ 0.049. The upper right inset shows a magnified view of Cp/T of the x = 0.049 sample around Tc. b Evolution of resistance and ZFC magnetic susceptibility in CaK(Fe1 − yCo y )4As4. Tc is suppressed by Co substitution and the kink-like feature at TN emerges in the resistance data similar to the effect of Ni substitution
Common phase diagram of Co-doped and Ni-doped CaKFe4As4. Doping CaKFe4As4 with either Co or Ni suppresses the superconducting transition temperature, Tc, and stabilizes a hedgehog spin-vortex crystal below TN. \(T_{\mathrm{c}}^{\rm R}\) and \(T_{\mathrm{c}}^{\rm M}\) were determined by resistance and magnetization measurements, respectively. The Ni-concentration x, on the upper axis, is scaled by a factor of two with respect to the Co-concentration, y, which maps the transition temperatures of the two series onto each other. This scaling is consistent with an electron doping picture where Ni substitution adds twice as many electrons per atom as Co. Transition temperatures of CaK(Fe1 − xNi x )4As4 determined by heat capacity, Mössbauer spectroscopy, and nuclear magnetic resonance are consistent with this phase diagram. Horizontal error bars represent the standard deviation of 12 composition points for each sample. Vertical error bars indicate transition width
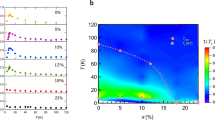
Consistent observation of a transition at TN in both doping series calls for investigation of its nature. Figure 4a–c shows high-energy x-ray diffraction results from CaK(Fe0.951Ni0.049)4As4. The peak shapes (Fig. 4c) are unchanged below TN = 53 K indicating an absence of lattice distortions. No superlattice peaks appear in the low-temperature diffraction patterns in the lower halves of Fig. 4a,b. These results suggest that the geometry and multiplicity of the chemical unit cell are unchanged. 57Fe Mössbauer spectroscopy on crystals of CaK(Fe0.951Ni0.049)4As4 in Fig. 4d reveals clear structure in the spectra below 55 K demonstrating a hyperfine field, Hhf, at the Fe-sites, i.e., magnetic order. A fit of the spectrum at base temperature suggests a Hhf distribution centered around 3 T (corresponding to ~0.2 μB ordered moment28) and in-plane orientation of the iron moments. The temperature dependence of Hhf (Fig. 4f) is characteristic of a second-order phase transition, consistent with heat capacity. 75As nuclear magnetic resonance (NMR) is employed to probe the Hhf at the inequivalent As1 and As2 sites of the CaKFe4As4 structure. Figure 4e reveals a finite Hhf || c at As1 (close to K) and Hhf = 0 at As2. The temperature dependence of Hhf at As1 mirrors that at the Fe site (Fig. 4f). The assignment of As1 and As2 is made following ref. 23. As Mössbauer and NMR measurements reveal the behavior of the majority of Fe-atoms, we associate the observed magnetism with the CaK(Fe, Ni)4As4 phase identified by high-energy x-ray diffraction.
Experimental insights into the nature of the magnetic phase of CaK(Fe0.951Ni0.049)4As4 below TN = 53 K. a, b Single crystal HHL and HK0 diffraction patterns at 300 K (upper halves) and 30 K (lower halves). No additional diffraction peaks appear at 30 K, counter-indicating a chemical superlattice. The Be sample enclosure produces diffraction rings. c 220 and 200 diffraction peaks (integrated azimuthally) vs. plane spacing d. The peak shapes remain unchanged below TN placing an upper relative limit of 4 × 10−4 on lattice distortions in either direction. d 57Fe Mössbauer spectra on a mosaic of 34 single crystals. Broadening of the absorption peak on cooling through TN indicates a hyperfine field, Hhf, produced by an ordered moment at the Fe-sites. The ratios of the peaks in the fitted sextet (solid lines) reveal that these ordered moments lie perpendicular to the crystallographic c-axis. e Field-swept 75As (gyromagnetic ratio, γ/2π = 7.2919 MHz/T) nuclear magnetic resonance (NMR) spectra obtained at f = 43.2 MHz with applied magnetic field, H, along the crystallographic c-axis (upper three spectra) and with H ⊥ c (bottom spectrum). Simulated peaks from the two inequivalent As1 and As2-sites are denoted by hues of blue and green, respectively. Above TN each As site produces a central peak (shaded area) and a pair of electric quadrupole satellites. With H || c, the As1 triplet splits into two triplets on cooling through TN indicating presence of a Hhf component parallel to c at half of the As1-sites and antiparallel to c at the other half. The As2 triplet remains un-split. With H ⊥ c, neither triplet is split at 11 K indicating an absence of in-plane hyperfine fields at either As site. f The temperature dependence of \(\left| {{\boldsymbol{H}}_{{\mathrm{hf}}}} \right|\) at the Fe (squares, from Mössbauer) and As1-sites (circles, from NMR), consistent with a second-order magnetic phase transition at TN. The error bars represent standard fitting error (57Fe) and estimated uncertainty (75As)
Discussion
Our experimental results are inconsistent with the previously observed magnetic phases in the FeSCs: SSDW and SCDW. First, the Mössbauer spectra cannot be described by the moment motif of the SCDW phase where half the Fe-sites would experience Hhf = 0 (Fig. 1b). In addition, the distribution and direction of Hhf at As-sites inferred from NMR spectra rules out the SSDW, SCDW, and “loops” SVC phases (see Fig. 1a, b, d and Supplemental Material). Furthermore, the diffraction data in Fig. 4 are inconsistent with an orthorhombic distortion. Of the possibilities depicted in Fig. 1, only SVC-type order remains (Fig. 1c). To systematically consider the possible magnetic phases of CaK(Fe0.951Ni0.049)4As4, a representation analysis of CaKFe4As4’s magnetic space group, P4/mmm1’, was performed, similar to ref. 29. There are 96 commensurate magnetic structures allowed for the chemical structure21 of CaKFe4As4. Possible incommensurate magnetic phases are discussed in Supplemental Information (see Supplemental Information). Only 24 structures retain the original tetragonal chemical unit cell as suggested by the diffraction results. All of these are accessible by a second-order phase transition (see Supplemental Information) and have one common magnitude for all iron moments. However, the ordered Fe moments in eight of these (including ferromagnetism and Néel order) are normal to the Fe-planes, inconsistent with the Mössbauer results. The remaining 16 structures are all modifications of SVC order. There are two motif variations,13 “hedgehog” with M i || Q i (Fig. 1c) and “loops” with M i ⊥ Q i (Fig. 1d). Each variation can be centered on either As1 or As2 and can have four different stacking patterns along the crystallographic c-axis (see Supplemental Information). Only the hedgehog SVC, with the centering depicted in Fig. 1c, is consistent with the Hhf at As1 observed by NMR.
We argue that this peculiar, non-collinear magnetic phase is stabilized by the specific crystal structure of CaKFe4As4. The inequivalence of the staggered As sites (Fig. 1e) generates a symmetry-breaking field that couples to the spin vorticity, M 1 × M 2 , characteristic of SVC order (see Supplemental Materials). One possible mechanism is the electrostatic coupling of the As atoms to spin current loops associated with the magnetic moment motif12 (Fig. 1f). These spin currents generate an electric field analogous to the magnetic field produced by an electric current.30 The resulting electrostatic force couples the asymmetric shifts of the As atoms to the spin currents. The preference for the hedgehog SVC variation over loops variation is likely a consequence of spin–orbit coupling, which generally favors M i || Q i , observed experimentally in the case of the SSDW order of the parent AeFe2As2 compounds,3 and theoretically in ref. 9.
Our identification of a hedgehog SVC order in Co-doped and Ni-doped CaKFe4As4 sheds new light on the curious landscape of magnetic phases in FeSCs arising from two magnetic propagation vectors. Previous results indicate that SSDW and SCDW phases have comparable energies in some hole-doped FeSCs.14,15,16,17 Our observation in effectively hole-doped CaKFe4As4 reveals that SVC order is competitive (with SSDW and SCDW) as well and demonstrates the sensitivity of magnetism in FeSCs. This phenomenon is confirmed by first-principle calculations, which can compare the energies of different magnetic configurations. Previous calculations needed to invoke a SVC-like order to reproduce the structural collapse of CaKFe4As4 under pressure.31 Our calculations reveal that SSDW and hedgehog SVC are nearly degenerate for pure CaKFe4As4 but the latter prevails upon electron doping (see Supplemental Information). The near-degeneracy of these magnetic phases provides an enlarged configuration space for magnetic fluctuations which may have profound implications for magnetically mediated superconducting pairing.32,33
Co-doped and Ni-doped CaKFe4As4, then, is the missing link in the evolution of magnetic order in the AeFe2As2 systems. Alternating cation layers in the CaKFe4As4 structure generate the appropriate symmetry breaking field to stabilize the predicted SVC phase. Therefore, this family of compounds is an ideal platform to probe the relative stability of SSDW and SVC states. Although the relation between the SVC magnetism and the superconducting state needs to be determined in detail, we note that the spin resonance observed by neutron scattering in pure CaKFe4As4 suggests similarities to other FeSCs.24
In conclusion, we confidently identified a hedgehog SVC in Co-doped and Ni-doped CaKFe4As4. The chemical structure of CaKFe4As4 and spin–orbit coupling conspire to stabilize this phase further exposing the complex magnetism in FeSCs. This first experimental realization of SVC order in a magnetic superconductor opens a new platform to study multi-component, non-collinear magnetic phases and their interplay with superconductivity.
Methods
Single crystals of Co-doped and Ni-doped CaKFe4As4 were grown out of a high-temperature solution rich in transition-metals and arsenic similar to the procedure used for the pure compound.22,34 Transition-metal arsenides precursors, M0.512As0.488 (M = Fe, Co, Ni), were synthesized from ground arsenic lumps (Alfa Aesar 99.9999%) and transition-metal powders [Fe (Alfa Aesar 99.9 + % metals basis), Co (Alfa Aesar 99.8% metals basis), Ni (Alfa Aesar 99.9% metals basis)] in a rotating fused-silica ampoule in a purpose-built tube furnace as described in ref. 35. The iron and cobalt reactions were held at 565 °C for 900 min then 900 °C for 600 min before the furnace was switched off. The nickel version was held at 720 °C for 600 min instead of 900 °C because nickel arsenides melt at lower temperatures. Ground transition-metal arsenide precursors M0.512As0.488, potassium metal globs (Alfa Aesar 99.95%), and distilled calcium metal pieces (Ames Laboratory, Materials Preparation Center 99.9%) were loaded into alumina Canfield Crucible Sets (LSP Industrial Ceramics, Inc.).36 Batches were about 2 g of material with a molar ratio of K: Ca: Fe0.512As0.488 : M0.512As0.488 = 1.2 : 0.8 : 20(1 − x) : 20x. This crucible set was sealed in a tantalum metal tube and then in an argon-filled, fused-silica ampoule. These ampoules were heated in a box furnace using the optimum profile described in ref. 34. The final temperature varied from 920 to 933 °C depending on how the transition metal ratio shifted the solidification temperature. After 1–2 h at this final temperature the growth assembly was removed from the furnace, inverted into a centrifuge, and spun to decant the remaining liquid off the crystals.36 The metallic plate-like crystals obtained were often smaller than those of undoped CaKFe4As4 and cleaved easily along the (001) planes.
Chemical analysis of freshly-cleaved crystal surfaces was performed by wavelength-dispersive x-ray spectroscopy on a JEOL JXA-8200 microprobe system. Twelve points were analyzed for each sample. CaWO4, KAlSi3O8, Co metal, Ni metal and FeAs were used as standards.
Electrical resistance was measured in a standard four-contact geometry with Pt-wires bonded to the samples with silver paint. A Lakeshore Model 370 AC resistance bridge was employed and the temperature environment was provided by a Janis Research SHI-950T 4 K closed-cycle refrigerator.
Magnetization measurements were performed in a Quantum Design, Magnetic Property Measurement System in a clear plastic straw. The samples were zero-field cooled before applying a magnetic field of 50 Oe parallel to the plate-shaped crystals.
The heat capacity data of the samples was measured using a hybrid adiabatic relaxation technique of the heat capacity option in a Quantum Design, Physical Properties Measurement System.
High-energy x-ray diffraction measurements were performed on the six-circle diffractometer at end station 6-ID-D at the Advanced Photon Source, Argonne National Laboratory, using an x-ray energy of E = 100.34 keV and a beam size of 100 × 100 μm2. The CaK(Fe0.951Ni0.049)4As4 single-crystal sample was mounted on the cold finger of a He closed-cycle refrigerator. The sample was enclosed by a Be dome and He exchange gas was used to ensure the thermal equilibrium. Diffraction patterns were recorded using a MAR345 image plate detector positioned at 1.474 m from the sample. The distance was determined from measurement of powder patterns of CeO2 standard from the National Institute of Standards and Technology. The detector was operated with a pixel size of 100 × 100 μm2, and patterns were recorded while rocking the sample through two independent angles up to ±2.8° about the axes perpendicular to the incident beam.
57Fe Mössbauer spectroscopy measurements were performed in a SEE Co. conventional, constant acceleration type spectrometer in transmission geometry. The 57Co in Rh source was maintained at room temperature. Thirty-four cleaved crystals of CaK(Fe0.951Ni0.049)4As4 were fixed to a paper disk with Apiezon N grease. An effort was made to keep gaps between crystals to a minimum and the part of the disk not covered by crystals was coated with tungsten powder (Alfa Aesar 99.9% metals basis). This mosaic was positioned so that the gamma ray beam was parallel to the crystallographic c-axis. The sample temperature was maintained using a Janis SHI-850-5 closed cycle refrigerator with vibration damping. The driver velocity was calibrated using an α-Fe foil. The Mössbauer spectra were fitted using the commercial software package MossWinn 4.0Pre.37 Below TN, the Mössbauer spectra can be modeled with a single value of hyperfine field (reported in Fig. 4f) and an increased linewidth with respect to the paramagnetic state. Alternatively, they may be described by a temperature independent linewidth and a distribution of hyperfine fields. Both approaches suggest that there is a distribution of H hf at the Fe sites in the magnetic phase.
NMR measurements of CaK(Fe0.951Ni0.049)4As4 (total mass ~5 mg) were carried out on 75As (I = \(\frac{3}{2}\), γ/2π = 7.2919 MHz/T, Q = 0.29 barns) by using a lab-built, phase-coherent, spin-echo pulse spectrometer. The spin echo was observed with a sequence of \(\frac{\pi }{2}\) pulse (2.2 μs) - 30 μs - π pulse (4.4 μs). The 75As-NMR spectra were obtained at a fixed frequency, f = 43.2 MHz, with sweeping the magnetic field up to 8.25 T. The magnetic field was applied parallel or perpendicular to the crystallographic c-axis. 75As NMR spectra was simulated with two (for H || c above TN and H ⊥ c) or three (H || c below TN) sets of peaks with distinct values of Hhf and quadrupole interaction, νQ. The ratio of the integrated area of As1 to As2 is 1:1 in all the spectra. The ratio of As1 with −Hhf to +Hhf is also 1:1 in the spectra for H || c below TN.
The symmetry analysis was performed used the ISOTROPY software suite38 to systematically analyze the possible magnetic orders of CaKFe4As4 with magnetic space group P4/mmm1’. A detailed description of the analysis is presented in Supplemental Material (see Supplemental Information).
In the first-principles calculations, the effect of electron doping on the magnetic properties of CaKFe4As4 was studied using the virtual crystal approximation (VCA) and the all-electron full-potential linearised augmented-plane wave basis (Elk FP-LAPW code) (URL http://elk.sourceforge.net/. ELK FP-LAPW code). The structure parameters were fixed at the measured room-temperature values for undoped samples.39
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Pallecchi, I., Eisterer, M., Malagoli, A. & Putti, M. Application potential of Fe-based superconductors. Supercond. Sci. Technol. 28, 114005 (2015).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Lorenzana, J., Seibold, G., Ortix, C. & Grilli, M. Competing orders in FeAs layers. Phys. Rev. Lett. 101, 186402 (2008).
Eremin, I. & Chubukov, A. V. Magnetic degeneracy and hidden metallicity of the spin-density-wave state in ferropnictides. Phys. Rev. B 81, 024511 (2010).
Brydon, P. M. R., Schmiedt, J. & Timm, C. Microscopically derived Ginzburg-Landau theory for magnetic order in the iron pnictides. Phys. Rev. B 84, 214510 (2011).
Cvetkovic, V. & Vafek, O. Space group symmetry, spin-orbit coupling, and the low-energy effective Hamiltonian for iron-based superconductors. Phys. Rev. B 88, 134510 (2013).
Wang, X., Kang, J. & Fernandes, R. M. Magnetic order without tetragonal-symmetry-breaking in iron arsenides: microscopic mechanism and spin-wave spectrum. Phys. Rev. B 91, 024401 (2015).
Christensen, M. H., Kang, J., Andersen, B. M., Eremin, I. & Fernandes, R. M. Spin reorientation driven by the interplay between spin-orbit coupling and Hund’s rule coupling in iron pnictides. Phys. Rev. B 92, 214509 (2015).
Gastiasoro, M. N. & Andersen, B. M. Competing magnetic double-Q phases and superconductivity-induced reentrance of C 2 magnetic stripe order in iron pnictides. Phys. Rev. B 92, 140506 (2015).
Hoyer, M., Fernandes, R. M., Levchenko, A. & Schmalian, J. Disorder-promoted C 4-symmetric magnetic order in iron-based superconductors. Phys. Rev. B 93, 144414 (2016).
Fernandes, R. M., Kivelson, S. A. & Berg, E. Vestigial chiral and charge orders from bidirectional spin-density waves: Application to the iron-based superconductors. Phys. Rev. B 93, 014511 (2016).
O’Halloran, J., Agterberg, D. F., Chen, M. X. & Weinert, M. Stabilizing the spin vortex crystal phase in two-dimensional iron-based superconductors. Phys. Rev. B 95, 075104 (2017).
Allred, J. M. et al. Double-Q spin-density wave in iron arsenide superconductors. Nat. Phys. 12, 493–498 (2016).
Avci, S. et al. Magnetically driven suppression of nematic order in an iron-based superconductor. Nat. Commun. 5, 3845 (2014).
Böhmer, A. E. et al. Superconductivity-induced re-entrance of the orthorhombic distortion in Ba1−xK x Fe2As2. Nat. Commun. 6, 7911 (2015).
Hassinger, E. et al. Expansion of the tetragonal magnetic phase with pressure in the iron arsenide superconductor Ba1−xK x Fe2As2. Phys. Rev. B 93, 144401 (2016).
Mallett, B. P. P., Pashkevich, Y. G., Gusev, A., Wolf, T. & Bernhard, C. Muon spin rotation study of the magnetic structure in the tetragonal antiferromagnetic state of weakly underdoped Ba1−xK x Fe2As2. EPL 111, 57001 (2015).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Blomberg, E. C. et al. In-plane anisotropy of electrical resistivity in strain-detwinned SrFe2As2. Phys. Rev. B 83, 134505 (2011).
Iyo, A. et al. New-structure-type Fe-based superconductors: CaAFe4As4 (A = K, Rb, Cs) and SrAFe4As4 (A = Rb, Cs). J. Am. Chem. Soc. 138, 3410–3415 (2016).
Meier, W. R. et al. Anisotropic thermodynamic and transport properties of single-crystalline CaKFe4As4. Phys. Rev. B 94, 064501 (2016).
Cui, J. et al. Magnetic fluctuations and superconducting properties of CaKFe4As4 studied by 75As NMR. Phys. Rev. B 96, 104512 (2017).
Iida, K. et al. Spin resonance in the new-structure-type iron-based superconductor CaKFe4As4. Journal. Phys. Soc. Jpn. 86, 093703 (2017).
Zinth, V., Dellmann, T., Klauss, H.-H. & Johrendt, D. Recovery of a parentlike state in Ba1−xK x Fe1.86Co0.14As2. Angew. Chem. Int. Ed. 50, 7919–7923 (2011).
Canfield, P. C. & Bud’ko, S. L. FeAs-based superconductivity: a case study of the effects of transition metal doping on BaFe2As2. Annu. Rev. Cond. Matt. Phys. 1, 27–50 (2010).
Liu, Y. et al. RbEu(Fe1−xNix)4As4: from ferromagnetic superconductor to superconducting ferromagnet. Phys. Rev. B 96, 224510 (2017).
Rotter, M. et al. Spin-density-wave anomaly at 140 K in the ternary iron arsenide BaFe2As2. Phys. Rev. B 78, 020503 (2008).
Khalyavin, D. D. et al. Symmetry of reentrant tetragonal phase in Ba1−xNa x Fe2As2: magnetic versus orbital ordering mechanism. Phys. Rev. B 90, 174511 (2014).
Sun, Q., Guo, H. & Wang, J. Spin-current-induced electric field. Phys. Rev. B 69, 054409 (2004).
Kaluarachchi, U. S. et al. Pressure-induced half-collapsed-tetragonal phase in CaKFe4As4. Phys. Rev. B 96, 140501 (2017).
Hirschfeld, P. J., Korshunov, M. M. & Mazin, I. I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 74, 124508 (2011).
Chubukov, A. Pairing mechanism in Fe-based superconductors. Annu. Rev. Condens. Matter Phys. 3, 57–92 (2012).
Meier, W. R., Kong, T., Bud’ko, S. L. & Canfield, P. C. Optimization of the crystal growth of the superconductor CaKFe4As4 from solution in the FeAs-CaFe2As2-Kfe2As2 system. Phys. Rev. Mater. 1, 013401 (2017).
Ran, S. Combined Effects of Post-growth Thermal Treatment and Chemical Substitution on Physical Properties of CaFe 2 As 2 . Ph.D. thesis, Iowa State University (2014).
Canfield, P. C., Kong, T., Kaluarachchi, U. S. & Jo, N. H. Use of frit-disc crucibles for routine and exploratory solution growth of single crystalline samples. Philos. Mag. 96, 84–92 (2016).
Klencsár, Z. MossWinn 4.0 Manual http://www.mosswinn.com/english/index.html (2016).
Campbell, B. J., Stokes, H. T., Tanner, D. E. & Hatch, D. M. ISODISPLACE: a web-based tool for exploring structural distortions. J. Appl. Cryst. 39, 607–614 (2006).
Mou, D. et al. Enhancement of the superconducting gap by nesting in CaKFe4As4: a new high temperature superconductor. Phys. Rev. Lett. 117, 277001 (2016).
Acknowledgements
The authors would like to acknowledge W. Straszheim for his expertise and assistance with chemical analysis, D. S. Robinson for experimental support of the x-ray scattering study, and T. Kong for assistance during early stages of sample preparation. We also acknowledge discussions with E. Berg, A. Chubukov, and S. Kivelson. Work at the Ames Laboratory was supported by the Department of Energy, Basic Energy Sciences, Division of Materials Sciences & Engineering, under Contract No. DE-AC02-07CH11358. WRM was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4411. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. VB and RV are supported by the Deutsche Forschungsgemeinschaft (DFG) under grant SFB/TRR49. RMF is supported by the Office of Basic Energy Sciences, U.S. Department of Energy, under award DE-SC0012336. PPO acknowledges support from Iowa State University Startup Funds.
Author information
Authors and Affiliations
Contributions
P.C.C., S.L.B. and W.R.M. initiated this work; W.R.M. grew the samples; W.R.M., Q.P.D., A.K., S.L.B., A.S., K.K., and A.E.B. performed measurements and analyzed the data; V.B., R.V., P.P.O., C.D.B., and R.M.F performed the theoretical interpretations and computational work; W.R.M. and A.K. performed the symmetry analysis; R.V., R.M.F., A.I.G., Y.F., A.E.B., and P.C.C. guided the work; W.R.M., A.K., R.M.F., and A.E.B. drafted the manuscript and all authors participated in the writing and review of the final draft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meier, W.R., Ding, QP., Kreyssig, A. et al. Hedgehog spin-vortex crystal stabilized in a hole-doped iron-based superconductor. npj Quant Mater 3, 5 (2018). https://doi.org/10.1038/s41535-017-0076-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0076-x
This article is cited by
-
Temperature Dependence of the Superconducting Order Parameter in Stoichiometric Alkali Metal-Based Pnictide EuCsFe\(_4\)As\(_4\)
Journal of Superconductivity and Novel Magnetism (2024)
-
Multiple magnetic orders in LaFeAs1-xPxO uncover universality of iron-pnictide superconductors
Communications Physics (2022)
-
Iron pnictides and chalcogenides: a new paradigm for superconductivity
Nature (2022)