Introduction

The tendency for the resistivity of metals to increase with temperature, T, is generally understood on the basis of Boltzmann transport theory. In turn, for the requisite distribution function to be consistent with quantum mechanics, it must be possible to construct electron wave-packets with well-defined velocities and positions. Consequently, at best, Boltzmann theory is applicable only so long as the mean-free-path, \(\ell\), is long compared to the Fermi wavelength, i.e. \(\ell \gg 2\pi /{k}_{{\rm{F}}}\). There are other conditions for the validity of Boltzmann theory, such as the Mott-Ioffe-Regel (MIR) condition \(\ell \gg a\), which allows one to ignore interband scattering. While there is no upper bound on the magnitude of a metallic resistivity, any time ρ ≳ ρ B/N (where N is the number of bands), and it cannot be interpreted in terms of freely propagating quasiparticles, which are occasionally scattered. Here, ρ B signifies a characteristic resistivity derived from Boltzmann theory extrapolated to the limit \(\ell \mathrm{=2}\pi /{k}_{{\rm{F}}}\), i.e. ρ B = ħ/e 2 in d = 2 and ρ B = (4/3)[h/e 2 k F] in d = 3, while the MIR limit1 corresponds to ρ MIR = had−2/e 2.

In practice, many simple metals melt before ρ gets to be as large as ρ B. Of those that reach this value, there are apparently two distinct classes: (a) Those that exhibit “resistivity saturation,” i.e. the resistivity becomes decreasingly T dependent as T gets large, with a value that appears to approach a finite asymptotic limit at large T. (b) Those “bad metals” (ref. 2) for which ρ B does not appear to be a relevant scale at all, in which the resistivity is still a strongly increasing function of T even when ρ > ρ B. Understanding bad metallic behavior, and its complement, resistivity saturation, remains one of the major open problems in the theory of metals.2,3,4 Transport regimes beyond the quasi-particle paradigm have attracted much interest in recent years.5,6,7,8,9,10,11,12,13,14,15,16,17

Since its discovery in the 1970s,18,19,20 several theories have been proposed to explain resistivity saturation;21,22,23,24,25,26,27,28,29,30,31 however, to this day, no consensus has emerged. In particular, several key theoretical issues have not been resolved; for example, in cases where 2π/k F and a are parametrically different from each other (as in a weakly doped semiconductor), it is not clear whether the saturation value of the resistivity corresponds to \(\ell \approx 2\pi /{k}_{{\rm{F}}}\), \(\ell \approx a\), or neither. Empirically, the resistivity of saturating metals is often well-described by the “parallel resistor” formula,32

$$\rho {(T)}^{-1}={\rho }_{{\rm{ideal}}}{(T)}^{-1}+{\rho }_{{\rm{sat}}}^{-1},$$
(1)

with ρ ideal(T) = ρ 0 + γT representing the semiclassical contribution of disorder and phonon scattering (where ρ 0 and γ are constants), and ρ sat the saturation resistivity. This formula suggests the existence of a parallel conduction channel, which is not affected by phonon scattering. Moreover, it is typically the case that ρ sat ~ ρ B ~ ρ MIR.

In this paper, we present a tractable microscopic electron–phonon model with a resistivity that saturates at a value ρ sat that is independent of the strength of the electron–phonon coupling, but that does depend on the electron density and the band structure; in that sense, while numerically it is not all that different from either ρ B or ρ MIR, conceptually it does not quite correspond to either. In addition, two distinct conductivity channels appear: one which continuously decreases with increasing temperature, and another which saturates at high temperatures. This is reminiscent of the parallel resistor formula, Eq. (1). In this model, the saturation of resistivity is not due to a bound on the quasiparticle lifetime or its mean free path, but on the existence of a T-independent phonon-assisted conduction channel.

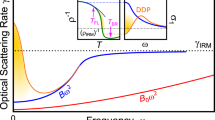
Our model consists of N identical electronic bands coupled to N 2 optical (Einstein) phonon modes. As in ref. 33, we consider the problem in the limit that the dimensionless electron–phonon coupling (defined in Eq. (7) below) is large, λ ≫ 1. This is a necessary condition to insure that Boltzman transport theory breaks down at a temperature, T B ~ E F/λ, that is small compared to the Fermi energy E F. We shall see that at low electron density, where the bandwidth Λ ≫ E F, it is possible to look separately at the crossover that occurs at T B and at T MIR ~ Λ/λ, while still maintaining T ≪ E F. There are generically many unwanted complications, including possible lattice instabilities, associated with large λ; however, the combination of the large N limit taken here, and the fact that we are studying phenomena at relatively high temperatures makes them irrelevant in the present study (In the electron–phonon coupling, we keep only linear order in the phonon displacement, and neglect higher-order terms. This is justified in the large-N limit, since the typical magnitude of the coupling term to any single phonon mode is α(T/(KN))1/2, which is smaller than other electronic scales (e.g., E F)). Representative results for the resistivity as a function of temperature are shown in Fig. 1.

Fig. 1
figure 1

Resistivity per flavor, in units of 1/e 2 N, as a function of λT/Λ in the N→∞ limit, where Λ is the bandwidth, for a two-dimensional square lattice. The blue and green curves are, respectively, for a density per site in each flavor, n = 1/3 and n = 1/8. At the lower density, the resistivity exceeds the saturating value and then approaches it with increasing temperature from above

Full size image

In order to verify that the behavior we find is not an artifact of the large N limit, we have performed numerical Monte-Carlo simulations of the model at finite values of N. The results (see Fig. 6) confirm that the qualitative behavior of the N→∞ solution are already apparent for N as small as four.

Results

Model

Our system is composed of N ≫ 1 electron bands, which interact with N 2 optical, dispersionless phonon modes, in d spatial dimensions. The phonons couple to the electron kinetic energy. In this type of large-N expansion, inspired by the work of Fitzpatrick et al.,34 the phonon modes act as a momentum and energy bath for the electrons; thus, it is particularly suitable for studying the effects of the phonons on the electrons, while neglecting the back action of the electrons on the phonons. (This is probably a reasonable assumption in the relevant temperature range even for “realistic” small values of N).

The action is given by

$$S={S}_{{\rm{el}}}+{S}_{{\rm{ph}}}+{S}_{{\rm{int}}},$$
(2)

where

$${S}_{{\rm{el}}}=\sum _{a\mathrm{=1}}^{N}\sum _{{\nu }_{n}}\int \frac{{d}^{d}k}{{(2\pi )}^{d}}{c}_{a}^{\dagger }({\bf{k}},\,{\nu }_{n})[i{\nu }_{n}-{\xi }_{{\bf{k}}}]{c}_{a}({\bf{k}},\,{\nu }_{n})$$
(3)

is the electronic part of the action,

$${S}_{{\rm{ph}}}=\sum _{a,b\mathrm{=1}}^{N}\sum _{{\omega }_{n},r}\int \frac{{d}^{d}q}{{(2\pi )}^{d}}\frac{1}{2}[M{\omega }_{0}^{2}+M{\omega }_{n}^{2}]{|{X}_{ab}^{r}({\bf{q}},{\omega }_{n})|}^{2}$$
(4)

is the phononic part, and

$${S}_{{\rm{int}}}=\frac{\alpha }{\sqrt{\beta N}}\sum _{a,b\mathrm{=1}}^{N}\sum _{{\nu }_{n},{\nu }_{m},r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi)}^{2d}}{g}_{r}({\bf{k}},{\bf{k}}^{\prime} )\times {X}_{ab}^{r}({\bf{k}}-{\bf{k}}{^{\boldsymbol{\prime} }},\,{\nu }_{n}-{\nu }_{m})[{c}_{a}^{\dagger }({\bf{k}},{\nu }_{n}){c}_{b}({\bf{k}}{^{\boldsymbol{\prime}}},\,{\nu }_{m})+a\leftrightarrow b]$$
(5)

is the electron–phonon interaction term. Here, \({c}_{a}^{\dagger }({\bf{k}},{\nu }_{n})\) creates an electron of wavevector k, Matsubara frequency ν n , and flavor 1 ≤ a ≤ N; the electronic dispersion is ξ k  = ϵ(k)−μ(T), with ϵ(k)∈[−Λ/2, Λ/2] (where Λ is the bandwidth). μ(T) is the chemical potential at temperature T, and β = 1/T. \({X}_{ab}^{r}({\bf{q}},{\omega }_{n})\) is the Fourier transform of the phonon displacement operator of flavor a,b and mode r; M is the ionic mass, and ω 0 is the phonon frequency. α is the electron–phonon coupling strength. The dimensionless form factor g r (k, k′) satisfies g r (k′, k) = g r (k, k′)*. Throughout the paper, we set k B , ħ and the lattice spacing a to 1.

For concreteness, we use a d = 2 tight binding model on a square lattice; we expect the results to be qualitatively insensitive to this particular choice. We consider a case, where the phonons couple to the electron bond density (as in the Su–Schrieffer–Heeger model35). There is one phonon mode centered on every bond; we label the phonon modes by the direction of the bond, r = x, y. The electron–phonon coupling term in the Hamiltonian has the form

$$\frac{\alpha }{\sqrt{4N}}\sum _{a,b,j,r}{X}_{ab,j}^{r}({c}_{a,j}^{\dagger }{c}_{b,j+r}+h\mathrm{.}c\mathrm{.}+a\leftrightarrow b),$$
(6)

where j labels lattice sites. This term describes coupling of the phonon modes to the electron bond density. The corresponding electron–phonon form factor in Eq. (5) is \({g}_{r}({\bf{k}},\,{\bf{k}}^{\prime} )={e}^{i{k}_{r}a}+{e}^{-i{k^{\prime} }_{r}a}\). This is in contrast to the models studied by Millis et al.30 and by us,33 where the phonons couple to the electron site density. The electronic dispersion is given by \(\varepsilon ({\bf{k}})=-2t{\sum }_{r}\,\cos ({k}_{r}).\)

As in ref. 33, we focus on the range of temperatures ω 0 ≪ T ≪ E F , where ω 0 is the mean optical phonon frequency and E F is the Fermi energy. The first inequality implies that the phonon variables can be treated as classical (our results are accurate to leading order in ω 0/T), and the second that the electron fluid is still highly quantum mechanical.

We define the dimensionless electron–phonon coupling constant as

$$\lambda =\frac{{\alpha }^{2}\nu }{M{\omega }_{0}^{2}},$$
(7)

with ν the density of states at the Fermi energy. We will be particularly interested in the case in which λ is large compared to unity, so that although T is small compared to E F , λT can be larger E F and even larger than the bandwidth Λ, i.e. there exists an interesting “high temperature” regime in which E F/λ ≪ T ≪ E F, where the quasiparticle scattering rate is larger than its energy, but the electrons are nevertheless quantum mechanically degenerate.33

The current operator of this system is given by

$${\bf{J}}(i{\omega }_{n})=e\sum _{a,{\nu }_{n}}\int \frac{{d}^{d}k}{{(2\pi )}^{d}}{{\bf{v}}}_{{\bf{k}}}{c}_{a}^{\dagger }({\bf{k}},\,{\nu }_{n}){c}_{a}({\bf{k}},\,{\nu }_{n}+{\omega }_{n})+\frac{e\alpha }{\sqrt{\beta N}}\sum _{a,b,{\nu }_{n},{\nu }_{m},r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{X}_{ab}^{r}({\bf{k}}-{\bf{k}}{^{\boldsymbol{\prime} }},\,{\nu _n}-{\nu _m}) \times (\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}^{\prime} })[{c}_{a}^{\dagger }({\bf{k}},\,{\nu }_{n}){c}_{b}({\bf{k}}{^{\boldsymbol{\prime} }},\,{\nu }_{m}+{\omega }_{n})+a\leftrightarrow b]\equiv {{\bf{J}}}^{0}+{{\bf{J}}}^{1};$$
(8)

here v k = (∂ϵ)/(∂k). This can be derived, for instance, by coupling the electrons to a vector potential A by replacing c a (k) → c a (k−e A) in Eq. (2), and differentiating the action with respect to A. J 0 derives directly from the non-interacting electrons’ kinetic energy, while J 1 represents a phonon-assisted conductivity channel.

Single electron properties

Taking the limit N→∞ allows us to solve the model (2) order by order in 1/N. Just as in ref. 34, the full set of rainbow diagrams contributes to the electron self-energy to lowest order in 1/N. This results in a self-consistent Dyson’s equation for the fermion self-energy:

$$\Sigma ({\bf{k}},\,\omega )=\frac{\lambda T}{\nu }\sum _{r}\int \frac{{d}^{d}k^{\prime} }{{(2\pi )}^{d}}\frac{{|{g}_{r}({\bf{k}},{\bf{k}}^{\prime} )|}^{2}}{\omega -{\xi }_{{\bf k}}^{\boldsymbol{{\prime} }}-\Sigma ({\bf{k}}^{\prime} ,\,\omega )}.$$
(9)

For solids with a constant density of electrons, this equation must be solved simultaneously with the equation for the density per flavor

$$n=\int \frac{{d}^{d}k}{{(2\pi )}^{d}}\langle {c}_{\alpha }^{\dagger }({\bf{k}}){c}_{\alpha }({\bf{k}})\rangle \approx \int \frac{{d}^{d}k}{{(2\pi )}^{2}}{\int _{-\infty }^{0}}\frac{d\omega }{2\pi }A({\bf{k}},\,\omega ),$$
(10)

which fixes the temperature dependent chemical potential μ. Here A(k,ω) = −2Im(1)/(ω−ξ k −Σ(k,ω)) is the spectral function. For details of the solution, see supplementary material; here, we state the results.

At low temperatures, λT ≪ E F , the chemical potential is approximately temperature-independent and the scattering rate on the Fermi surface, given by 1/τ(k) = −Im[Σ(k,ω = 0)] ≡ Σ′′(k,ω = 0), rises linearly with temperature: 1/τ(k) = πλT/ν∑ r ∫ k′ |g r (k,k')|2 δ(ξ k'), with ∫ k  ≡ ∫d d k/(2π)d; this is the famous semiclassical result.36

In the high temperature limit, λT ≫ Λ, the temperature dependence is given by (see details in the supplementary material)

$$\mu (T)={\tilde{\mu }}_{0}\sqrt{\lambda T/\nu },\sum ({\bf{k}},\,\omega ;\,T)=\sum ^{\sim }({\bf{k}},\,\tilde{\omega })\sqrt{\lambda T/\nu },$$
(11)

where \(\tilde{\omega }=\omega /\sqrt{\lambda T/\nu }\), and \({\tilde{\mu }}_{0},\tilde{\Sigma }({\bf{k}},\omega )\) are found by solving the coupled, temperature independent equations

$$\tilde{\Sigma }({\bf{k}},\,\tilde{\omega })=\sum _{r}\int \frac{{d}^{d}k^{\prime} }{{(2\pi )}^{d}}\frac{{|{g}_{r}({\bf{k}},{\bf{k}}')|}^{2}}{\tilde{\omega }+{\tilde{\mu }}_{0}-\tilde{\Sigma }({\bf{k}}',\,\tilde{\omega })},n=\int \frac{{d}^{d}k^{\prime} }{{(2\pi )}^{d}}{\int _{-\infty }^{{\tilde{\mu }}_{0}}}\frac{d\tilde{\omega }}{2\pi }{\rm{Im}}\left[\frac{1}{\tilde{\omega }-\tilde{\Sigma }({\bf{k}}',\,\tilde{\omega })}\right].$$
(12)

At high temperature, a crossover occurs to a square-root dependence of the self energy on the temperature. The crossover occurs around λT ≈ μ.

Conductivity

The D.C. conductivity is given by summing over three different channels (see Fig. 2):

$$\sigma ={\sigma }^{00}+2{\sigma }^{01}+{\sigma }^{11}\,\,,\,{\rm{where}}\kern-12pc{\sigma }^{ij}=-\mathop{\lim}\limits_{\omega \to 0}\frac{{\rm{Im}}{\Pi }^{ij}(\omega )}{\omega },{\Pi }^{ij}(\omega )={\langle {J}_{x}^{i}(i{\omega }_{n}){J}_{x}^{j}(-i{\omega }_{n})\rangle |}_{i{\omega }_{n}\to \omega +i\delta }\mathrm{.}$$
(13)
Fig. 2
figure 2

The four diagrams which contribute to the conductivity. Bold lines are renormalized electron propagators, dashed lines are phonon propagators, and the full and dashed wiggly lines correspond to J 0 and J 1, respectively. The green and blue areas represent the renormalized J 0 and J 1 vertex functions, respectively

Full size image

The full details of the calculation of the conductivity are given in the supplementary material; here, for simplicity, we will sketch the calculations without vertex corrections. Vertex corrections are included in the figures, and do not change the behavior qualitatively.

σ 00 has been calculated in ref. 33 neglecting vertex corrections, it is given by

$${\sigma }^{00}(T)=-\mathop{\lim}\limits_{\omega \to 0}\frac{{\rm{Im}}{\Pi }^{00}({i\omega }_{n}\to \omega +i\delta ,\,T)}{\omega }=-\mathop{\lim}\limits_{\omega \to 0}\frac{{e}^{2}N}{\beta \omega }{\rm{Im}}\sum _{{\nu }_{n}}\int \frac{{d}^{d}k}{{(2\pi )}^{d}}{v}_{{\bf{k}}}^{2}\times {\mathcal{G}}(i{\nu }_{n},\,{\bf{k}}){\mathcal{G}}(i{\nu }_{n}+i{\omega }_{n},\,{\bf{k}}){|}_{i{\omega }_{n}\to \omega +i\delta }\approx \frac{{e}^{2}N}{4\pi }\int \frac{{d}^{d}k}{{(2\pi )}^{d}}{v}_{{\bf{k}}}^{2}{[A({\bf{k}},\omega \mathrm{=0})]}^{2}\mathrm{.}$$
(14)

\({\mathcal{G}}(i{\nu }_{n},k)\) is the fully dressed electron Green’s function. In the last line of Eq. (14), we have inserted the spectral representation of the Green’s function, performed the Matsubara summation over ν n (see, e.g.,37), and used the fact that the Fermi function n F (ϵ) obeys (dn F (ϵ))/(dϵ) ≈ −δ(ϵ) in the regime T ≪ E F , assuming that A(k,ω) changes slowly on the scale of T (This is justified because, at low temperature, A(k,ω) varies on the scale of Σ′′(ω = 0,T ≪ E F /λ) ~ λT, assumed to be much larger than T. [Here we have assumed that the density of states, and hence Σ′′(ω), vary slowly around zero energy on the scale of T]. At high temperature the spectral function varies on the scale of Σ′′(ω = 0,T ≫ Λ/c)~((λT)/(ν))1/2 ≫ T [see Eq. (11)]).

σ 11 is the channel responsible for resistivity saturation. For simplicity, we present here only the contribution of the diagram (C) in Fig. 2, that does not contain vertex corrections to leading order in 1/N; diagram (D) is calculated in the supplementary material, and found to be negligible. To lowest order in 1/N, the Π11 correlation function is given by

$${\Pi }^{11}(i{\omega }_{n})={e}^{2}N{\alpha }^{2}\sum _{r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{\left|\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}^{\prime} }\right|}^{2}\kern-2.5pc \times \frac{1}{{\beta }^{2}}\sum _{n,m}G({\bf{k}},\,i{\nu }_{n})G({\bf{k}}^{\boldsymbol{\prime} },\,i{\nu }_{m}+i{\omega }_{n})D({\bf{k}}-{\bf{k}}^{\boldsymbol{\prime} },\,i{\nu }_{n}-i{\nu }_{m}),$$
(15)

with D(q,iωn) the phonon propagator, which is unrenormalized to lowest order in 1/N. To leading order in ω 0/T, this results in

$${\Pi }^{11}(i{\omega }_{n})={e}^{2}N\frac{\lambda T}{\nu }\sum _{r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{\left|\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}^{\prime} }\right|}^{2}\times \frac{1}{\beta }\sum _{n}G({\bf{k}},\,i{\nu }_{n})G({\bf{k}}^{\boldsymbol{\prime} },\,i{\nu }_{n}+i{\omega }_{n})={e}^{2}N\frac{\lambda T}{\nu }\sum _{r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{\left|\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}^{\prime} }\right|}^{2}\times \int \frac{d{\varepsilon }_{1}}{2\pi }\frac{d{\varepsilon }_{2}}{2\pi }A({\bf{k}},\,{\varepsilon }_{1})A({\bf{k}}^{\boldsymbol{\prime} },\,{\varepsilon }_{2})\frac{{n}_{F}({\varepsilon }_{1})-{n}_{F}({\varepsilon }_{2})}{i{\omega }_{n}+{\varepsilon }_{1}-{\varepsilon }_{2}},$$
(16)

where we have inserted the spectral representation and performed the Matsubara summation. Therefore, again using the fact that T ≪ E F ,

$${\sigma }^{11}=\frac{{e}^{2}N\lambda T}{4\pi \nu }\sum _{r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{\left|\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}'}\right|}^{2}\times A({\bf{k}},\,0)A({\bf{k}}^{\boldsymbol{\prime} },\,0)\mathrm{.}$$
(17)

At high temperatures it is possible to approximate \(A({\bf{k}},0)=-2\sqrt{\frac{\nu }{\lambda T}}{\rm{Im}}\frac{1}{{\tilde{\mu}}_{0}-\tilde{\Sigma}({\bf{k}},0)}\), with both \(\tilde{\Sigma }({\bf{k}},0)\) and \({\tilde{\mu }}_{0}\) temperature independent. Therefore, at high T, σ 11 saturates to a temperature and coupling strength-independent value.

A plot of σ 00 and σ 11, calculated for a two-dimensional tight binding model, is shown in Fig. 3. The contribution of the {01} channel, σ 01 (calculated in the supplementary material) is found to be negligible compared to max [σ 00,σ 11], both at low and high temperatures.

Fig. 3
figure 3

The σ 00 and σ 11 conductivities per band. σ 00 falls as 1/T (although with different proportionality constants) in both temperature ranges ω 0 ≪ T ≪ μ/λ and μ/λ ≪ T ≪ μ. σ 11 grows in the lower range of T, then saturates as it approaches the value e 2/2π in the higher. This is calculated for a two-dimensional tight binding model, in which the phonon displacement couples to the nearest-neighbor hopping amplitude of the electrons

Full size image

Resistivity

Adding the three conductivity channels, the resistivity ρ = 1/σ of the model is shown in Fig. 1. For ω 0 ≪ T ≪ E F/λ, the {00} channel dominates, and the resistivity rises linearly with temperature:

$$\rho (T\ll {E}_{{\rm{F}}}/\lambda )\approx 1/{\sigma }^{00}\approx \frac{2\pi }{{e}^{2}N}\frac{\lambda T}{{\bar{v}}_{{\rm{F}}}^{2}\nu },$$
(18)

where \({\bar{v}}_{F}^{2}=1/\pi {\int }_{{\bf{k}}}[{v}_{{\bf{k}}}^{2}\delta ({\xi }_{{\bf{k}}})/{\sum }_{r}{\int }_{{\bf{k}}^{\boldsymbol{\prime} }}{|{g}_{r}({\bf{k}},{\bf{k}}^{\boldsymbol{\prime}})|}^{2}\delta ({\xi }_{{\bf{k}}'})]\). This is the Bloch–Grüneisen formula for T > ω 0.

At high temperatures, however, the linear increase in 1/σ 00 is offset by the parallel addition of the saturating {11} channel, the rapid growth of the resistivity is checked, and the resistivity saturates at the value

$${\rho }_{{\rm{sat}}}=\frac{\pi \hbar }{{e}^{2}N}{\left[\sum _{r}\int \frac{{d}^{d}k{d}^{d}k^{\prime} }{{(2\pi )}^{2d}}{\left|\frac{\partial {g}_{r}}{\partial {\bf{k}}}+\frac{\partial {g}_{r}}{\partial {\bf{k}}'}\right|}^{2}\right.\left.\times {\rm{Im}}\frac{1}{{\tilde{\mu }}_{0}-\tilde{\Sigma }({\bf{k}},0)}{\rm{Im}}\frac{1}{{\tilde{\mu }}_{0}-\tilde{\Sigma }({\bf{k}}',0)}\right]}^{-1}$$
(19)

Here, we have reintroduced ħ for clarity. From Eq. (19), it is clear that ρ sat is independent of temperature and of the electron–phonon coupling strength, λ. It does, however, depend on the form factor g r (k, k′) and on the electron density n [through the dependence of \(\tilde{\mu }\) and \(\tilde{\Sigma }({\bf{k}},0)\) on n, Eq. (12)]. In Fig. 4 we show1/ρ sat as a function of n in our model. ρ sat reaches a minimum close to h/(Ne 2) at half filling. Near n = 0 and n = 1, ρ sat diverges. (Note that within our model, in order to access the saturation regime in the limit n→0 while keeping T ≪ E F , one has to take λ→∞ while keeping λE F fixed.)

Fig. 4
figure 4

Saturation resistivity, ρ sat, as a function of the density of electrons per site per flavor

Full size image

At low fillings, the rapid decrease of σ 00 causes the resistivity to overshoot the saturating value, and the parallel addition of the channels causes the resistivity to decrease with temperature. In that case, the high temperature saturation value is approached from above (see Fig. 1). Such behavior has been observed in certain heavy fermion compounds.38

Optical conductivity

The optical conductivity σ(ω) can give insights into the physics of saturating metals and of bad metals.3, 4 In conventional metals, the optical conductivity displays a pronounced Drude peak at all accessible temperatures, while materials which approach the MIR limit have been argued to lose this coherent contribution. To gain further insights into the mechanism of the saturation in our model, we now examine the optical conductivity.

It is straightforward to extend the calculations described above to σ(ω) (see supplementary material for details). The optical conductivity as a function of frequency for several temperatures is shown in Fig. 5. At low temperatures, where σ 00 dominates, the conductivity shows a Drude peak, whose width is proportional to T. At high temperatures (within the saturating regime), on the other hand, the optical conductivity consists of a broad peak whose height is nearly temperature independent, while its width increases with temperature. This can be understood from the fact that, at asymptotically high temperatures, σ(ω) has support over a frequency range that scales with an effective bandwidth (λT/ν)1/2.

Fig. 5
figure 5

The optical conductivity σ(ω) for several temperatures. (inset) For low temperatures ω 0 ≪ T ≪ E F /λ, a distinct Drude peak appears in the spectrum, of width λT, and the conductivity vanishes for ω > Λ. At high temperatures, the Drude peak is lost, but σ(ω) has a clear structure on the scale of (λT/ν)1/2; the optical conductivity has finite support over the effective bandwidth (λT/ν)1/2 ≫ Λ. In this model, resistivity saturation implies that the zeroth moment of the conductivity grows with temperature

Full size image

Interestingly, this implies that the total spectral weight, defined as

$${\mu }_{0}={\int }_{0}^{\infty }\sigma (\omega )$$
(20)

increases with temperature. This is consistent with the sum rules concerning σ(ω), which within our model is given by

$${\mu }_{0}=-\frac{\pi }{2}{e}^{2}(\langle {K}_{0}\rangle +\langle {K}_{1}\rangle ),$$
(21)

where

$${K}_{0}=\sum _{{\bf{k}},a}\frac{{\partial }^{2}{\xi }_{{\bf{k}}}}{\partial {k}_{x}^{2}}{c}_{a}^{\dagger }({\bf{k}}){c}_{a}({\bf{k}}),\,\kern-10pc{K}_{1}=\frac{4\alpha }{\sqrt{N}}\sum _{{\bf{k}},{\bf{k}}',a,b,r}{\gamma }_{r}({\bf{k}},\,{\bf{k}}'){X}_{a,b}^{r}({\bf{k}}-{\bf{k}}')\times [{c}_{a}^{\dagger }({\bf{k}}){c}_{b}({\bf{k}})+h.c.].$$
(22)

Here, \({\gamma }_{r}({\bf{k}},\,{\bf{k}}^{\boldsymbol{\prime} })\equiv [{\partial }_{{k}_{x}}^{2}+{\partial }_{{k}_{x^{\prime} }}^{2}+2{\partial }_{{k}_{x}}{\partial }_{{k}_{x^{\prime} }}]{g}_{r}({\bf{k}},\,{\bf{k}}^{\boldsymbol{\prime}})\). It is the second term in Eq. (21) that is responsible for the increase of the spectral weight, μ 0 ∝ (T)1/2, for λT ≫ Λ. This reflects the fact that in this regime, the phonon-assisted hopping channel dominates the transport. In real materials, however, this behavior might be hard to observe, as it could be masked by high-energy features in σ(ω) due to inter-band transitions.

Numerics

The analytical results described above are confined to the N → ∞ limit. One may then ask to what extent the physics of a system with a finite number of electronic bands and phonon modes is captured by the N → ∞ picture. To assess this, we have performed numerical simulations of the model in Eq. (2) for finite values of N. The simulations are done by treating the phonons as a classical static field with a distribution that corresponds to the free energy of the system with a fixed phonon configuration, while the electrons are treated quantum mechanically. (See supplementary material for additional details of the simulations). The only approximation in this approach is to neglect the phonon dynamics, by taking ω 0→0. The problem can be solved fully quantum mechanically using quantum Monte Carlo (QMC), since the model (2) does not suffer from a sign problem (although then, calculating the conductivity requires an analytic continuation to real time). Ref. 24 demonstrated that at high temperatures, QMC results for a similar elecron–phonon model agree with the “semiclassical” approximation that neglects the phonon dynamics.

In Fig. 6, the resistivity as a function of temperature is shown for systems with N = 2, 4, 6, 8, along with the analytical N → ∞ result. The numerical results approach the N → ∞ curve, showing that the approach to the N → ∞ limit is not singular. It is also clear that signatures of saturation appear already at small N, rendering our analysis pertinent for physical systems.

Fig. 6
figure 6

Numerical results for the resistivity as a funciton of temperature. These results were obtained using a Monte Carlo simulation, treating the phonons classically and the electrons quantum mechanically

Full size image

Discussion

It has been argued that saturation is connected with a limit quantum mechanics imposes on the maximal quasiparticle scattering rate, or equivalently on the minimal mean free path. In our model, the inverse electron lifetime increases without bound as Σ′′(k,0)∝(T)1/2; this is clearly not the mechanism for saturation. However, the origin of the saturation is quantum mechanical—it relies on the finite bandwidth Λ of the system, and the saturation value is proportional to Planck’s constant h [Eq. (19)].

We can also address the question of whether the correct criterion for saturation is \(\ell \approx a\) or \(\ell \approx 2\pi /{k}_{{\rm{F}}}\), by looking at the low density limit where E F ≪ Λ. In this regime, we find two distinct crossovers that occur when T becomes comparable to E F/λ and Λ/λ, respectively. In the first of these crossovers, where the Boltzman approach breaks down, the slope of the linear increase of ρ deviates from its low-T value;33 in the second crossover, where the extrapolated mean free path satisfies \(\ell \approx a\), the saturation occurs. If E F and Λ are parametrically different from each other (as in lightly doped semiconductors), the resistivity may rise beyond the saturation value and then approach it from above (see Fig. 1).

The value of the resistivity at saturation is ha d−2/e 2 times a numerical factor [Eq. (19)] that depends on the electron density and the electron–phonon coupling form factor. The saturation value is not universal, although it is independent of the overall electron–phonon coupling strength.

Relation to other works

The (T)1/2-dependence of the self-energy at high temperatures has been found by Millis et al. 30 for an N = 1 electron–phonon system, using DMFT. The importance of the coupling of the phonons to the electronic kinetic energy was recognized by Calandra et al. 24 They used QMC to compute the resistivity of a five-fold degenerate electron band coupled to optical phonons via the hopping matrix elements and observed resistivity saturation. In contrast, in a model in which the phonons couple to the site energies, the resistivity did not saturate. They also observed that the resistivity saturation depends on the number of degenerate electronic bands.

Our analysis clearly elucidates why coupling to the kinteic energy is important; it is the conductance channel which originates form this coupling that causes the saturation. This gives a natural physical interpretation of the phenomenological parallel resistor formula. We note that the mechanism described in this work for resistivity saturation is different from the interpretation given in ref. 39, which is based on the conductivity f-sum rule. In particular, within our model, the integral of σ(ω) increases with temperature. This is due to an increase of the effective bandwidth with temperature (see Fig. 5).

The present results have potential relevance in a broader context. Recently, it has been conjectured that there is an upper bound to the rate of “scrambling” in any quantum system, given by Γ ≤ Γmax ≡ 2πT.40 A similar bound has been proposed for the “dephasing” rate, \({\Gamma }_{\varphi }\le {\mathcal{C}}T\) with \({\mathcal{C}}\) of the order of unity.41 However, the relation of this rate—and consequently of the corresponding bound—to important equilibration rates in solids remains an open question. In particular, the system we consider here displays relaxation rates that exceed this bound for large λ; in the temperature range ω 0 ≪ T ≪ E F/λ, both the single particle scattering rate and the current relaxation rate (i.e. the width of the Drude peak) are given by λT, while for E F/λ ≪ T ≪ E F the inverse of the single particle lifetime is (λT/ν)1/2. It would be interesting to study the scrambling dynamics in our model, and examining its relation to the physical response functions.

Another issue concerns phonon-drag, processes in which the momentum that has been transferred to the phonon bath is coherently returned to the electron fluid are suppressed by a power of 1/N in the present problem, (Phonon drag effects are also suppressed in powers of ω 0.) but can be studied by keeping higher order terms in the 1/N expansion. In the absence of a lattice, the total momentum of the system is conserved, and therefore the 1/N contribution to the conductivity would contains a δ-peak at ω = 0. However, umklapp processes are not expected to be small in the present system, as the phonons are thermally occupied throughout the Brillouin zone for T ≫ ω 0. These umklapp processes render the 1/N contribution at ω = 0 finite, enabling us to expand the conductivity order by order in 1/N. We plan to explore the 1/N corrections further in the near future.

Conclusions

We present a tractable electron–phonon model that displays resistivity saturation. At low temperatures, ω 0  ≪  T  ≪  E F/λ, the resistivity increases linearly with temperature, according to the semiclassical formula. At high temperatures, T ≫ Λ/λ, the resistivity saturates to a temperature and coupling strength-independent value. The saturation is not a result of a limit on the scattering rate, but due to the existence of an additional phonon-assisted conductivity channel that becomes effective at higher temperature. This gives a natural microscopic interpretation for the phenomenological parallel resistor formula.

Beyond the possible implications for the resistivity of metals, the analysis presented here, together with the one presented in ref. 33, provides examples of metallic transport in a regime that cannot be described in terms of coherent quasiparticles. It may be possible to extend this analysis, using an appropriate large-N limit, to other problems of unconventional transport, e.g., where the scattering is dominated by electron–electron interactions. We leave such extensions to future work.

Methods

In all analytic calculations, we have used the two dimensional tight-binding model presented in Eq. (6). Equation (9) for the self energy Σ(k, ω) was solved iteratively for a large number of ωs, and the chemical potential μ found by fixing the density, as described in Eq. (10). Vertex corrections were obtained through self-consistent equations, exact to lowest order in 1/N.

In the numerical simulation, a slightly different tight-binding model was used, with a next-nearest neighbor hopping parameter t′ = −t; this hopping parameter was introduced to suppress any instabilities arising from nesting of the Fermi surface. The phonon displacements were treated as classical fields, and the free energy was given by

$$F=\frac{1}{2}K\sum _{i,j,\alpha ,\beta ,r}{({X}_{i,j,\alpha ,\beta }^{r})}^{2}-T\sum _{n}\mathrm{log}(1+{e}^{(-{\varepsilon }_{n}-\mu )/T}),$$
(23)

where \({X}_{i,j,\alpha ,\beta }^{r}\) are the phonon displacement of flavor αβ at site i,j, of mode r, ϵ n are the eigenvalues of the single-particle Hamiltonian for the given phonon configuration, and μ is the chemical potential obtained by demanding constant filling. The ϵ n ’s are obtained by exact diagonalization.

All the calculations, in much more detail, appear in the supplementary material.

Change History

A correction to this article has been published and is linked from the HTML version of this article.