Electrical two-qubit gates within a pair of clock-qubit magnetic molecules

Abstract

Enhanced coherence in HoW₁₀ molecular spin qubits has been demonstrated by use of clock-transitions (CTs). More recently it was shown that, while operating at the CTs, it was possible to use an electrical field to selectively address HoW₁₀ molecules pointing in a given direction, within a crystal that contains two kinds of identical but inversion-related molecules. Herein we theoretically explore the possibility of employing the electric field to effect entangling two-qubit quantum gates within a 2-qubit Hilbert space resulting from dipolar coupling of two CT-protected HoW₁₀ molecules in a diluted crystal. We estimate the thermal evolution of T₁, T₂, find that CTs are also optimal operating points from the point of view of phonons, and lay out how to combine a sequence of microwave and electric field pulses to achieve coherent control within a switchable two-qubit operating space between symmetric and asymmetric qubit states that are protected both from spin-bath and from phonon-bath decoherence. This two-qubit gate approach presents an elegant correspondence between physical stimuli and logical operations, meanwhile avoiding any spontaneous unitary evolution of the qubit states. Finally, we found a highly protected 1-qubit subspace resulting from the interaction between two clock molecules.

Introduction

Electrical control of spins at the nanoscale offers significant architectural advantages in spintronics, because electric fields (E-fields) can be confined over shorter length scales than magnetic fields (B-fields)^1,2,3,4,5. In the context of qubits, the use of E-fields has been already suggested as a strategy to generate entangling two-qubit gates, either passing current pulses through molecules in single-molecule spintronics, or by applying E-fields in a P@Si crystal^6,7,8,9.

Magnetic molecules are considered as an ideal platform in this line since their spin Hamiltonian can be tailored by chemical design¹⁰. Constructing two-qubit gates has been already explored theoretically based on heterodimer systems, where the qubit states are defined as identical to the spin states of the individual molecular component^{11,12,13,14,15,16}. These schemes are generally affected by a weak “always-on” inter-qubit interaction that cannot be completely switched off due to residue dipolar coupling, which makes them hard to scale as it induces an unwanted two-qubit evolution of the wavefunction. Other strategies employ a single high-spin metal center that encodes multiple qubits, where most of the logical operation, both single-qubit and two-qubit, require a series of physical multi-step climbing on the energy levels of the molecule¹⁷. Implementing two-qubit logical gates as independent physical operations is challenging in practice.

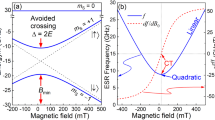
Another challenge for molecular spin qubits is that they exhibit fragile quantum coherence owing to the inevitable interaction with the environment (spin and phonon baths). A significant enhancement has been recently achieved via clock-transitions (CTs), which protect from magnetic noise^18,19,20. Nevertheless, at the CT field, the two-qubit states would present a vanishing first-order Zeeman effect and a vanishing magnetic moment, due to perfect mixing within a tunneling-splitting electronic spin doublet M_J = ± 4. We will explore herein how these limitations may be overcome by slightly moving away from the CT but preserving some coherent protection and, at the same time, the use of a directional E-field to electronically tune the transition frequencies of the two interacting qubit molecules.

The polyoxometalate molecular anion ${[{{{\rm{Ho}}}}{({{{{\rm{W}}}}}_{5}{{{{\rm{O}}}}}_{18})}_{2}]}^{9-}$ (abbreviated to HoW₁₀) with crystal structure ${{{\rm{N{a}}}_{9}[{Y}_{1-x}H{o}_{x}{({W}_{5}{O}_{18})}_{2}]\; \cdot \; 35{H}_{2}O}}$ (x = 1%) is a prime example of CT spin qubit¹⁸. The crystal unit cell contains two inversion-symmetry related HoW₁₀ anions, slightly distorted (D_4d symmetry) along their C₄ axes (Fig. 1a). The magnetic levels of a single HoW₁₀ can be described by a Hamiltonian, including crystal field, hyperfine, and Zeeman interactions:

$$\hat{H}=\mathop{\sum}\limits_{k=2,4,6}\mathop{\sum }\limits_{q=-k}^{k}{B}_{k}^{q}{\hat{O}}_{k}^{q}(J)+\hat{J}\cdot A\cdot \hat{I}+{\mu }_{B}{g}_{e}{B}_{0}\cdot \hat{J}-{\mu }_{N}{g}_{N}{B}_{0}\cdot \hat{I},$$

(1)

where, ${B}_{k}^{q}$ corresponds to the crystal-field parameters (CFPs) in the Extended Steven Operator notation (${\hat{O}}_{k}^{q}$). J and I are the total electronic and nuclear angular momentum, respectively, A denotes the isotropic hyperfine interaction, g_e (g_N) and μ_B (μ_N) correspond to the electronic (nuclear) gyromagnetic ratio and Bohr magneton, respectively. The low-energy region of interest comprises 16 electro-nuclear spin levels corresponding to the spin doublet M_J = ± 4 and a nuclear spin I = 7/2 (Supplementary Fig. 1). Each CT corresponds to an anticrossing between the 8th and the 9th levels (Supplementary Note 1).

Fig. 1: A weakly dipolarly coupled HoW₁₀-HoW₁₀.

a Nearest inversion-related HoW₁₀ pair within the crystal, illustrating their dipolar interaction. Their magnetic axes point in opposite directions. b Calculated energies (left axis) and mixing degree (right axis) of the eigenstates in terms of the $\left\vert {M}_{J}=\pm 4\right. >$ spin states of HoW₁₀ as a function of magnetic and electric fields. α and β are the eigenstate coefficients (i.e., $\Psi =\alpha \left\vert {M}_{J}=+4\right\rangle \pm \beta \left\vert {M}_{J}=-4\right\rangle$) The first CT is located at ${B}_{\min }$ = 24 mT. The calculated CT frequency is ≃ 11 GHz ( ≃9.1 GHz in experiment).

A recent experimental study showed that one can achieve coherent control over the spin of HoW₁₀ molecules by using an E-field pulse to manipulate the CT frequency²¹. This is realized in practice due to a strong spin–electric coupling (SEC), which arises from intrinsic symmetry breaking, a soft and electrically polarizable environment of the spin carriers, and a spin spectrum that is highly sensitive to distortions. This allows to selectively address the spins of identical HoW₁₀ molecules pointing at different directions.

In this work, we theoretically demonstrate the possibility of employing E-field pulses to effect entangling two-qubit quantum gates within a 2-qubit Hilbert space resulting from two neighboring CT-protected molecules of HoW₁₀. This involves finding a B-field constituting a compromise between keeping some of the protection from magnetic noise and allowing unitary evolution of the qubit states. We start with a theoretical estimate of the effect of temperature and B-field on the longitudinal (T₁) and transverse (T₂) relaxation times of a HoW₁₀ single qubit. Later, with the whole Hamiltonian, we indicate the conditions and procedure to implement arbitrary 2-qubit manipulations in this system.

Results

Single-qubit relaxation

Prior to addressing the two-qubit system (i.e., the two inversion-symmetry related HoW₁₀ units of the crystal cell), let us analyze the relaxation dynamics of an individual HoW₁₀ molecule. Note that, despite the CT protection, HoW₁₀ presents relatively short coherence times T₂(5K) ≃ 8 μs. We are interested in the role of temperature because of the lack of such information both in experiment and in theory, since previous works have focused on the role of the spin bath for this compound^22,23.

The dynamics of the entire system (electronic spins and phonons) can be described by the time evolution of the density operator, $\hat{\rho }(t)$.

$$\dot{\hat{\rho }}(t)=-\frac{\dot{\iota }}{\hslash }\left[\hat{H},\hat{\rho }(t)\right]$$

(2)

where $\hat{H}={\hat{H}}_{{{{\rm{S}}}}}+{\hat{H}}_{{{{\rm{ph}}}}}+{\hat{H}}_{{{{\rm{S-ph}}}}}$ is the total Hamiltonian describing the electronic spins (${\hat{H}}_{{{{\rm{S}}}}}$), the phonon bath (${\hat{H}}_{{{{\rm{ph}}}}}$) and their spin-bath interaction (${\hat{H}}_{{{{\rm{S-ph}}}}}$), respectively. When phonon dynamics is much faster than the spin relaxation (as it is the case here), the Born-Markov approximation is safely invoked integrating out the phonon component from the density matrix and making the problem purely electronic in the presence of a phonon bath²⁴. In this regime, the dynamics of the electronic spin states can be described by the reduced spin density operator (${\hat{\rho }}^{{{{\rm{S}}}}}$) within the Redfield equation in the eigenvector representation of the spin Hamiltonian ${\hat{H}}_{{{{\rm{S}}}}}$^25,26,27,28,

$${\dot{\rho }}_{ab}^{S}(t)=-\dot{\iota }{\omega }_{ab}{\rho }_{ab}-\mathop{\sum}\limits_{cd}{R}_{ab,cd}{\rho }_{cd}^{S}(t)$$

(3)

where ω_ab = (E_a − E_b)/ℏ, and E_a and E_b are the corresponding eigenvalues. R_ab,cd is the full Redfield tensor, which accounts for the system relaxation due to the interaction with the thermal bath. To evaluate the Redfield tensor, we need a spectral function for the bath, which is taken from ref. ²⁹, and the spin–phonon couplings, which are estimated from ab initio calculations (Supplementary Note 2).

We then solve the master equation (Eq. (3)) in time at different temperatures. T₁ and T₂ are thus extracted by fitting the exponential decays of magnetization at any temperature (Supplementary Note 3). The temperature evolution of T₁ predicted for HoW₁₀ (Fig. 2a) reveals an exponential T₁ – T dependence over the temperature range of 3–11 K. An Arrhenius fit of this Orbach process, T₁ ∝ exp (U_eff/k_BT), gives us an effective energy barrier U_eff of 34.5 cm⁻¹, which is virtually identical to the half of the energy of the lowest-frequency molecular vibration of HoW₁₀ (68.4 cm⁻¹)³⁰. This relation is in line with the interpretation of the under-barrier relaxation in molecular nanomagnets by Lunghi et al.²⁹ and indicates that the longitudinal relaxation of HoW₁₀ within the ground doublet is assisted by the lowest-frequency phonon mode at low temperatures. Our analysis also shows that T₂s are in the same order as for T₁s, both following the similar temperature trend (Fig. 2b). This behavior is in accordance with the observed drastic T₂ decrease upon heating¹⁸, demonstrating that T₂ is limited by T₁, which is mainly governed by the spin–phonon coupling with the lowest-frequency phonon mode. We notice that our calculation underestimates T₁ and T₂ compared with the experimental estimates determined at the CTs. This is partly due to the overestimation of spin–phonon couplings computed within a single HoW₁₀ model in gas phase. On the other hand, Raman relaxation processes (not considered here) may be important to estimate T₁ more precisely at low temperatures. However, a similar temperature dependence behavior for Orbach and Raman relaxation mechanisms have been shown as long as anharmonicity effects are included as here through the spectral density (Supplementary Equation 16)³¹.

Fig. 2: Longitudinal and transverse relaxation times.

a Calculated T₁ and bT₂ as a function of temperature at the CT and at 20 mT away from the CT. The dashed line in b indicates the T₂ limit of 300 μs estimated from nuclear spin bath in ref. ²². c T₁ and d T₂ divergences around the CT at different temperatures. The curves serve as a guide for the eye.

To gain an insight into the relaxation behavior in the vicinity of CTs, relaxation times are further analyzed at different B-fields and different temperatures. Figure 2c, d illustrate T₁, T₂ divergences with the longest relaxation times observed at the CT, i.e., $\left({T}_{1,2,Bz\ne 0}-{T}_{1,2,{{{\rm{CT}}}}}\right)/{T}_{1,2,{{{\rm{CT}}}}}$. This protection against vibrational decoherence at the CT coincides with the well-known T₂ protection from magnetic noise. The latter originates in the fact that the Ho spin possesses a vanishing magnetic moment resulted from mixing between $\left\vert {M}_{J}=+4\right\rangle$ and $\left\vert {M}_{J}=-4\right\rangle$ (Fig. 1b). When moving away from the CT, such mixing is broken by the Zeeman effect and thereby the dipolar decoherence is activated. Since we did not include dipolar decoherence in our model, it is not surprising that the calculated T₂ drop ( ~40%) at 10 mT away from the CT is less intense than the sharp T₂ divergence determined in experiments.

Two-qubit gates

To explore the possibility of coherent control over a 2-qubit Hilbert space, including generating entangled states, we considered two nearest HoW₁₀ qubits as indicated in Fig. 1a. With a protection of quantum coherence against spin-spin interactions, it has been demonstrated that T₂ was already saturated at 8 μs at 5 K in a 1% diluted HoW₁₀ crystal¹⁸, in which 0.01% abundance of HoW₁₀ dimers can be expected. This value falls into the dilution range of non-CT molecular spin qubits conventionally used for an optimum T₂^32,33. Although fully realistic, a technical difficulty of operating on molecular spin qubit pairs in a disordered, diluted system is that isolated molecules with similar transition energies will be far more abundant than molecule pairs. We will outline two independent ways of addressing this problem, based on initialization and on two-qubit gates.

Figure 3 a illustrates a schematic diagram for a general two-qubit system with identical (left) and inequivalent (right) qubits. In the symmetric scenario (at the CT and zero E-field in HoW₁₀ dimer case), one would define all four states as linear combination of the single-molecule states. Specifically, ${\left\vert 00\right\rangle }^{{{{\rm{s}}}}}$ and ${\left\vert 11\right\rangle }^{{{{\rm{s}}}}}$, which are energetically well-separated, correspond to the double ground and double excited states, respectively. In addition, ${\left\vert 01\right\rangle }^{{{{\rm{s}}}}}$ and ${\left\vert 10\right\rangle }^{{{{\rm{s}}}}}$ are degenerate in energy (Fig. 3a, left). Since the two molecules are identical and uncoupled, the states of the two molecules in ${\left\vert 01\right\rangle }^{{{{\rm{s}}}}}$ and ${\left\vert 10\right\rangle }^{{{{\rm{s}}}}}$ are separable and independent. That electronic situation is better understood not actually as a two-qubit system, but rather as two single-qubit systems that happen to be close to each other and function as two copies of the same qubit.

Fig. 3: Two-qubit entanglement generation.

a Scheme of the qubit states in absence and presence of an E-field. b Calculated dipolar exchange (${j}_{a,b}^{{{{\rm{dip}}}}}$) of the 16 spin levels of a HoW₁₀ molecule interacting with its neighboring molecule. The M_J = ± 4 levels with the same M_I are overlapped. c Energy levels of the coupled HoW₁₀ dimer in the presence of an E-field (300 V) with 2 mm interelectrode distance. The four operating levels are highlighted. The two middle levels (red and blue) are close to each other. d δf as a function of B-field with (red) and without (black) applied E-field. The SEC effect is indicated by their difference (blue). e The operating space around the first CT and the generation of the entangled states ${\Psi }_{23}^{\pm }$ and ${\Phi }_{14}^{\pm }$ at 12 mT. f Pulse sequence and g related initial and Bell states.

The key requirement for generating high-fidelity entangled states is to have distinguishable transitions and switchable (symmetric to asymmetric) operating qubit space. The former can be achieved through activating dipolar interaction. However, the symmetric scenario maintains under this circumstance, which resembles previous theoretical proposals^11,12,13,14. In order to have switchable qubit states, an E-field is introduced in our case, which alters the physical nature of the qubit space by breaking symmetry in ${\left\vert 01\right\rangle }^{{{{\rm{s}}}}}$ and ${\left\vert 10\right\rangle }^{{{{\rm{s}}}}}$ and gives rise to asymmetric states (Fig. 3a right).

This feature will be discussed in detail later. At this stage, let us first address the response of the HoW₁₀ dimmer system to an applied E-field. In reality, with an applied E-field, two symmetry-inversion HoW₁₀ molecules intrinsically experience opposite directions of the field but with the same magnitude, that is, +E for one molecule and -E for another. To simplify the description and calculations, we apply the net E-field effect on just one of the molecules, which is equivalent to the experimental scenario. The microscopic description in terms of an effective Hamiltonian of this system is as follows:

$${\hat{H}}^{{{{\rm{tot}}}}}={\hat{H}}_{{{{\rm{s}}}}}^{a}+{\hat{H}}_{{{{\rm{s}}}}}^{b}({{{\bf{E}}}})+{\hat{H}}^{{{{\rm{ex}}}}}$$

(4)

$${\hat{H}}^{{{{\rm{tot}}}}}={\hat{H}}_{{{{\rm{s}}}}}^{a}\otimes {{\mathbb{I}}}_{b}+{{\mathbb{I}}}_{a}\otimes {\hat{H}}_{{{{\rm{s}}}}}^{b}({{{\bf{E}}}})+{j}_{a,b}^{{{{\rm{dip}}}}}({{{\bf{B}}}}){J}_{a}\otimes {{\mathbb{I}}}_{b}\cdot {{\mathbb{I}}}_{a}\otimes {J}_{b}$$

(5)

where ${\hat{H}}_{{{{\rm{s}}}}}^{a}$ and ${\hat{H}}_{{{{\rm{s}}}}}^{b}({{{\bf{E}}}})$ are the spin (crystal field + hyperfine + Zeeman) Hamiltonians for HoW₁₀ sites a and electrically tuned b. The crystal-field parameters (CFPs) ${B}_{k}^{q}(E)$ are determined by establishing a relation between the given E-field and spin-energy levels (Methods and ref. ²¹). ${\hat{H}}^{{{{\rm{ex}}}}}$ denotes the interacting Hamiltonian, which accounts for the dipolar interaction (${j}_{a,b}^{{{{\rm{dip}}}}}$) between the two sites a and b. This dipolar interaction is dependent of B-field for a given two-site distance and orientations (Supplementary note 4), and vanishes at the CTs where the molecule is effectively diamagnetic (Fig. 3b).

Within the two dipolarly coupled molecules, the 16 levels of the individual molecules are combined into a 256 manifold (Fig. 3c). Without loss of generality, and since our Hamiltonian does not include terms that are extradiagonal in the nuclear spin, we consider only states involved in the first CT at ${B}_{\min }$ = 24 mT. Our operating two-qubit space is thus defined as the 4 levels resulting from the weak dipolar coupling between ${\left\vert {M}_{J} = \pm 4,{M}_{I} = -1/2\right\rangle }^{(a)}$ and ${\left\vert {M}_{J} = \pm 4,{M}_{I} = -1/2\right\rangle }^{(b)}$ states for sites a to b, respectively. We label these four electro-nuclear spin states as $\left\vert 00\right\rangle$, $\left\vert 01\right\rangle$, $\left\vert 10\right\rangle$, and $\left\vert 11\right\rangle$, independently of their physical nature, which will depend on the applied B- or E-field.

As discussed above, dipolar coupling is firstly needed to make two molecules inequivalent ($\delta f=E(\left\vert 10\right\rangle )-E(\left\vert 01\right\rangle )\, \ne \,0$), which is realized by moving B-field away from the CT region. Figure 3d illustrates δf as a function of the deviation from the CT. A high B-field is not actually required to achieve this inequivalence, indeed around B = 12 mT the exchange becomes non-negligible (δf = 0.1 MHz).

In the next step, an E-field is applied to generate asymmetric two-qubit states. In our working conditions (B-field = 12 mT, E-field = 300 V per 2 mm), the spins of the two molecules are coupled whereas the two qubits are uncoupled. This is evidenced by the fact that each of the states ${\left\vert 00\right\rangle }^{{{{\rm{as}}}}}$, ${\left\vert 01\right\rangle }^{{{{\rm{as}}}}}$, ${\left\vert 10\right\rangle }^{{{{\rm{as}}}}}$, ${\left\vert 11\right\rangle }^{{{{\rm{as}}}}}$ are eigenstates of the static Hamiltonian (eq. (4)), as can be seen from the wavefunction composition of the HoW₁₀ pair (Supplementary Tables 5–8). Besides, the two single-qubit frequencies ℏω₁ and ℏω₂ no longer correspond to the two single-molecule excitation energies, i.e., the eigenstates of the pair as our working space are not the eigenstates of the individual molecules due to dipolar interaction. Despite that, single-qubit addressability is not disturbed since transition frequencies are still distinct.

This framework is able to effect two-qubit gates, but first we briefly address the issue of initialization since our starting state would be the ${\left\vert -4,-1/2\right\rangle }^{(a)}\otimes {\left\vert -4,-1/2\right\rangle }^{(b)}$ (Fig. 3c, e, black). One can apply a sequence of pulses to transfer the population from the ground state of the bimolecular Hamiltonian to the ground state of our operating space. We estimated a possible initialization sequence by analyzing the wavefunction within a hyperfine basis ($\left\vert {M}_{I}^{a},{M}_{I}^{b}\right\rangle$, Supplementary Note 5). Note that the dipolar interactions are strong enough that this initialization step is able to distinguish between isolated molecules and pairs of neighboring HoW₁₀ qubits within the diluted crystal.

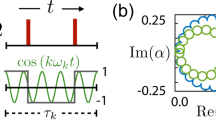
Here, we employ a specific case for illustration of single- and double-qubit operations, namely the generation of a Bell state involving ${\left\vert 00\right\rangle }^{{{{\rm{as}}}}}$ and ${\left\vert 11\right\rangle }^{{{{\rm{as}}}}}$. Once the initial state ${\left\vert 00\right\rangle }^{{{{\rm{as}}}}}$ is prepared, the E-field is turned on and a microwave π-pulse is applied to promote the ${\left\vert 00\right\rangle }^{{{{\rm{as}}}}}\to {\left\vert 10\right\rangle }^{{{{\rm{as}}}}}$ transition (Fig. 3e, f). The eigenstates after switching off the E-field are ${\left\vert 10\right\rangle }^{{{{\rm{s}}}}}$ and ${\left\vert 01\right\rangle }^{{{{\rm{s}}}}}$, thus Rabi-like oscillations start between ${\left\vert 10\right\rangle }^{{{{\rm{as}}}}}$ and ${\left\vert 01\right\rangle }^{{{{\rm{as}}}}}$. These coherent oscillations constitute a two-qubit SWAP gate by switching ${\left\vert 10\right\rangle }^{{{{\rm{as}}}}}\to {\left\vert 01\right\rangle }^{{{{\rm{as}}}}}$. More exactly, any desired rotation between these two states can be achieved by choosing the time of the operation, including the notable $\sqrt{SWAP}$ that together with single-qubit rotations forms a universal gate set. The $\sqrt{SWAP}$ gate operation would result in entangled states that can be read-out in Bell states as ${\Psi }_{23}^{\pm }=\frac{1}{\sqrt{2}}({\left\vert 01\right\rangle }^{{{{\rm{as}}}}}\pm {\left\vert 10\right\rangle }^{{{{\rm{as}}}}})$. To generate the desired Bell state, applying a π-pulse to ${\Psi }_{23}^{\pm }$ enables population transfer from ${\left\vert 10\right\rangle }^{{{{\rm{as}}}}}\to {\left\vert 00\right\rangle }^{{{{\rm{as}}}}}$ and ${\left\vert 01\right\rangle }^{{{{\rm{as}}}}}\to {\left\vert 11\right\rangle }^{{{{\rm{as}}}}}$ simultaneously because of their indistinguishable energy gaps, i.e., ${\Phi }_{14}^{\pm }=\frac{1}{\sqrt{2}}({\left\vert 00\right\rangle }^{{{{\rm{as}}}}}\pm {\left\vert 11\right\rangle }^{{{{\rm{as}}}}})$ (Fig. 3g). In other words, the transition frequency corresponding to each qubit is independent on the state of the two-qubit system. This unambiguous correspondence between logical operation and physical operation in a switchable two-qubit space constitutes a key difference between our proposal and previous approaches^{11,12,13,14,17,34,35}.

Physical implementation and pulse duration time

Let us give some estimates on practical details. The typical times for two-qubit gate operations will be given by the inverse of the interaction energy between the two molecular spins. With δf = 0.1 MHz at 12 mT as discussed above, a half rotation ($\sqrt{SWAP}$) would take in the order of 5 μs. The duration of microwave π-pulses (800 ns) was used in experiment to selectively excite qubits with narrow frequency around 3 MHz in the presence of the E-field²¹. Thus, the overall time needed (≃7 μs) for the pulse sequence illustrated in Fig. 3f is comparable to the T₂ value at 5 K. However, our calculations above show that the phonon-mediated decoherence below 3 K would be so weak that T₂ would rise to the order of 1 ms, indicating that the decoherence caused by the spin bath would dominate. The nuclear spin bath had been previously estimated to produce a T₂ ≃ 300 μs²², and the electron spin bath can be conveniently lowered by dilution if needed, meaning a conservative estimate of T₂ ≃ 30 μs should be easily achievable, and at the same time sufficiently longer than our estimated operation time.

The pair of states ${\left\vert 10\right\rangle }^{{{{\rm{as}}}}}$ and ${\left\vert 01\right\rangle }^{{{{\rm{as}}}}}$ merit a separate discussion. We have employed them here as two of the four states in a two-qubit system, but they also could be employed as an exceptionally protected single qubit (3rd-CT, Supplementary Fig. 11), with the other states being auxiliary. The idea that inter-qubit dipolar interactions and spin-phonon interactions need to be suppressed, and the proposal to do that by having antiferromagnetically ordered spin qubits via chemical design has been around for some time now³⁶. A similar strategy has been achieved experimentally in so-called flip-flop qubits⁴. One can appreciate the unusual protection against magnetic noise in the energy differences in Fig. 3d, and in the energy levels themselves in Supplementary Figs. 8 and 9.

As mentioned above, a key difficulty from working with pairs of magnetic entities within a diluted crystal is getting past the signal from the monomers, which will be statistically much more abundant. To supress single-qubit signal one needs to design pulse sequences, as in the example above, where all single-qubit operations add up to full 2π single-qubit rotations, so all the single qubits will be back to the ground state and not contribute to the detected signal. For qubit pairs, which experience two-qubit rotations, the same pulse sequence results in non-trivial operations. The extension of the same strategy to other quantum circuits is discussed in Supplementary Note 6, where other challenges for this scheme that may arise from the low symmetry of the crystal structure are discussed, together with possible strategies to address them.

Discussion

Our work presents a general methodology to investigate the possibility of generating entanglement in a 2-qubit Hilbert space constructed from two molecular spin qubits. To do so, one must determine the qubit relaxation times, and the details of the pulse sequence, including transition frequencies and pulse duration times. Of course, to obtain a reliable entangled state, relaxation times place an upper limit to total pulse duration times. Here, we investigated a CT qubit in HoW₁₀. The inversion-symmetric HoW₁₀ pair in a diluted crystal offers several features including the robust coherence close to the CTs, the strongest spin-electric response and the resulting switchable operating space between symmetric and asymmetric two-qubit states. Our results offers a promising strategy towards the use of HoW₁₀ molecular spin qubits in constructing a fully addressable two-qubit quantum processor, which not only avoids the “always-on” inter-qubit interaction by local E-field control, but also realizes one-to-one correspondence between logical and physical operations.

The approach presented in the present study can be employed to CT and non-CT systems. Further, our scheme can be directly employed to study the recently discovered Lu (II) CT system and its viability for entanglement generation¹⁹. Finally, note that the existence of a highly protected subspace might be exploited for further schemes in a way that this two-qubit system can be considered as two physical qubits able to temporarily store a single logical qubit, as an approach to built-in quantum error protection.

Methods

Ab initio calculations

The time-independent electronic structure of HoW₁₀ was computed using the multiconfigurational Complete Active Self-Consistent Field Spin-Orbit (CASSCF-SO) method as implemented in the OpenMOLCAS program package (version 18.09)³⁷. The molecular geometry was extracted from the single-crystal X-ray structure. Scalar relativistic effects were taken into account with the Douglas-Kroll-Hess transformation using the relativistically contracted atomic natural orbital ANO-RCC basis set with VDZP quality for all atoms. The active space consisted of 10 electrons on the 7 f-orbitals of Ho³⁺ ion. The molecular orbitals were optimized at the CASSCF level in a state-average (SA) over 35 quintets of the ground state term (L = 6 for Ho³⁺). The wave functions obtained at CASSCF were then mixed by spin–orbit coupling by means of the RASSI approach. The crystal-field parameters (CFPs) used for the system Hamiltonian (Eq. (1)) were calculated using SINGLE_ANISO module implemented in OpenMOLCAS³⁸. .

DFT calculations

The structural optimization of the crystallographic coordinates (in vacuum) and the vibrational modes calculations were carried out at DFT level using the Gaussian16 package in its revision A.03³⁹. Vibrational frequency calculations were performed using both the fully optimized structure and the X-ray crystal structure with no optimization. The PBE0 hybrid exchange-correlation functional was used for both optimization and frequency calculations in combination with Stuttgart RSC ANO basis set with effective core potential (ECP) for the Ho³⁺ cation. CRENBL basis set have been used for W with corresponding ECP potential and 6-31G(d,p) basis set had been used for oxygen. An “ultra-fine” integration grid and “very tight” SCF convergence criterion were applied. Dispersion effects were taken into account using the empirical GD3BJ dispersion correction.

Spin–electric couplings

To quantify the spin–electric couplings (SEC), we established a relation between the change in the dipole moment and spin-energy levels. As the dipole moment depends on the electronic cloud distribution, it will be directly affected by an induced E-field. To quantify the change of dipole moment, we used vibrational normal mode basis, as they are orthogonal, and we know for fact that each molecular perturbation can be decomposed of linear combination of normal basis. A central assumption in our methodology is that the rise in potential energy (${U}_{\alpha }=\frac{1}{2}\kappa {q}_{\alpha }^{2}$) due to the displacement of the atomic positions -in the form of a harmonic oscillator- is exactly matched by the stabilization of the potential energy (U_E = − p ⋅ E) due to the change in the molecular electric dipole in presence of an external electric field. In absence of E-field, spin-energy levels in lanthanide-based complexes can be characterized by time-independent crystal-field Hamiltonian ${\hat{H}}_{{{{\rm{CF}}}}}(J)$,

$${\hat{H}}_{{{{\rm{CF}}}}}(J)=\mathop{\sum}\limits_{k=2,4,6}\mathop{\sum }\limits_{q=-k}^{k}{B}_{k}^{q}{\hat{O}}_{k}^{q}(J)$$

(6)

where ${B}_{k}^{q}$ and ${\hat{O}}_{k}^{q}(J)$ correspond to the crystal-field parameter and the Stevens operator of rank ‘k’ respectively, and ‘J’ is total angular momentum. From eq. (6), it is evident that external E-field will modify the crystal-field parameters; i.e., “${B}_{k}^{q}\to {B}_{k}^{q}({{{\bf{Q}}}}(E))$” and Hamiltonian takes the form ${\hat{H}}_{{{{\rm{CF}}}}}(J)\to {\hat{H}}_{{{{\rm{CF}}}}}(J,{{{\bf{Q}}}}(E))$, where Q(E) accounts for the perturbative displacement caused by the change in the electronic cloud as a consequence of the E-field.

To numerically simulate this effect, we firstly distort the molecular geometry along the displacement vector for each normal mode α. The distortions are quantified by zero-point displacement for each normal mode, i.e., ${q}_{\alpha }=\pm \sqrt{\hslash \omega /{\kappa }_{\alpha }}$, here κ_i is the spring mass constant, which can be easily extract from DFT calculations. At each distorted geometry, we compute the dipole moment ‘p_α’ by single-point calculations in the presence of the environment described as a point-charge approximation. The obtained ‘p_α’ is then used in E(q_α) = − U_α/∣Δp_α∣ to quantify how much distortion q_α is produced in each normal mode “α” by an induced E-field. The effective total distortion will be a linear combination of orthogonal basis defined in the normal mode basis:

$${{{\bf{Q}}}}(E)=\mathop{\sum}\limits_{\alpha }{q}_{\alpha }(E)={q}_{1}(E)+{q}_{2}(E)+\ldots +{q}_{3N-6}(E)$$

(7)

where q_α(E) is the distortion induced at a given electrical field for the normal mode α, which can be further expressed in terms of normal vector as:

$${{{{\bf{q}}}}}_{\alpha }={q}_{\alpha }\left(\begin{array}{c}{{{{\bf{n}}}}}_{x,\alpha }\\ {{{{\bf{n}}}}}_{y,\alpha }\\ {{{{\bf{n}}}}}_{z,\alpha }\end{array}\right)$$

(8)

n_x,y,z,α are the normal vector coordinates in x, y, and z direction. Lastly, the effective total distortion (Q(E)) for given E-field is added to the equilibrium molecular geometry to re-compute the spin-energy levels at the CASSCF level.

Spin vibrational couplings

The interaction of the electronic spins with the nuclear degrees of freedom (phonons) also known as spin–phonon couplings (SPC) is a source of decoherence in molecular qubits. Spin, phonons, and spin-phonon Hamiltonians are defined below. (Note that the spin Hamiltonian is equivalent to the CF Hamiltonian previously described.)

$${\hat{H}}_{{{{\rm{S}}}}}=\mathop{\sum}\limits_{k=2,4,6}\mathop{\sum }\limits_{q=-k}^{k}{B}_{k}^{q}{\hat{O}}_{k}^{q}(J)$$

(9)

$${\hat{H}}_{{{{\rm{ph}}}}}=\mathop{\sum}\limits_{\alpha }\hslash {\omega }_{\alpha }({n}_{\alpha }+1/2)$$

(10)

$${\hat{H}}_{{{{\rm{S-ph}}}}}=\mathop{\sum}\limits_{k=2,4,6}\mathop{\sum }\limits_{q=-k}^{k}{\left(\frac{\partial {B}_{k}^{q}}{\partial {q}_{\alpha }}\right)}_{0}{\hat{q}}_{\alpha }{\hat{O}}_{k}^{q}(J)$$

(11)

ω_α denotes the frequency for mode α whereas n_α corresponds to the phonon level. ${\hat{q}}_{\alpha }$ denotes the a dimensional phonon coordinate and the term ${\left(\frac{\partial {B}_{k}^{q}}{\partial {q}_{\alpha }}\right)}_{0}$ is the SPC constant for a given phonon-α. To evaluate this coupling term, we start by computing the zero-point energy displacements; i.e., ${q}_{\alpha }=\sqrt{\hslash {\omega }_{\alpha }/{k}_{\alpha }}$, where k_α is the spring mass constant for a given phonon-α. We then distort the equilibrium molecular geometry q_eq within a limit of −q_α → + q_α along the displacement vectors n_x,y,z for each mode-α using: q_dist,α = q_eq + q_jn_x,y,z. For each distorted geometry q_dist,α, we performed ab initio electronic structure calculations (CASSCF-SO) and extracted the CFPs (${B}_{q}^{k}$) in Steven’s operator definition. The obtained CFPs are fitted with second order polynomials to evaluate the first-order SPC for a given phonon, i.e., ${\left(\frac{\partial {B}_{k}^{q}}{\partial {q}_{\alpha }}\right)}_{0}$.