High fidelity two-qubit gates on fluxoniums using a tunable coupler

Abstract

Superconducting fluxonium qubits provide a promising alternative to transmons on the path toward large-scale superconductor-based quantum computing due to their better coherence and larger anharmonicity. A major challenge for multi-qubit fluxonium devices is the experimental demonstration of a scalable crosstalk-free multi-qubit architecture with high-fidelity single-qubit and two-qubit gates, single-shot readout, and state initialization. Here, we present a two-qubit fluxonium-based quantum processor with a tunable coupler element. We experimentally demonstrate fSim-type and controlled-Z-gates with 99.55 and 99.23% fidelities, respectively. The residual ZZ interaction is suppressed down to the few kHz levels. Using a galvanically coupled flux control line, we implement high-fidelity single-qubit gates and ground state initialization with a single arbitrary waveform generator channel per qubit.

Introduction

Superconducting qubits have become one of the most successful platforms for quantum computing during the past decade. One of the pillars of this success was the development of the transmon qubit¹. The typical transmon-based toolkit consists of a coplanar waveguide (CPW) resonator for dispersive readout² and capacitive coupling that facilitates two-qubit gates³. One of the key limitations of transmon-based quantum computing is dielectric loss, which limits the qubit coherence time. Incremental progress in material science and fabrication technology over the years has enabled an increase in coherence times from few microseconds⁴ to hundreds of microseconds^5,6. Despite this remarkable progress, dielectric loss is still a major issue on the route to large-scale quantum computing with superconducting qubits. Another fundamental issue with transmon qubits is their low relative anharmonicity, which leads to longer gate times and, ultimately, lower gate fidelities. Nevertheless, transmon qubits have been hugely successful in the development of noisy intermediate-scale quantum information processing devices^7,8. Recent implementations of two-qubit gates on transmons demonstrate two-qubit gate fidelities around 99.5%^{9,10,11,12,13,14}. Another major issue for large-scale devices is crosstalk suppression. Among transmon qubits, one of the most critical types of crosstalk is static ZZ interaction. Recently, tunable couplers have been widely used as a tool to mitigate ZZ crosstalk in a scalable and effective way^{15,16,17,18,19,20}.

Development towards large-scale quantum computing motivates the search of multi-qubit architectures with better gate fidelities and simpler control systems.

Superconducting fluxonium qubits^21,22,23 could provide a possible alternative to the transmon path due to their lower transition frequencies and high coherence properties. Additionally, when operated at their lower sweet spot, fluxonium qubits exhibit coherent suppression of quasiparticle loss in the phase-slip junction^24,25. Microwave-activated CZ gates²⁶ have already been demonstrated on the fluxonium platform in a 3D cavity. Another example of high-fidelity two-qubit gates²⁷ has been shown in a more scalable approach with two qubits coupled to separate readout resonators, integrated on a single chip. Development of a tunable capacitive coupling architecture could provide means for Fluxonium-based NISQ devices.

In this paper, we experimentally demonstrate high-fidelity two-qubit gates between low-frequency fluxonium qubits using a tunable capacitive coupler setup shown in Fig. 1a, which was proposed earlier in our theoretical work²⁸. Both qubits and coupler are modified fluxonium circuits with additional harmonic modes. The computational qubits are operated at the flux degeneracy point where the qubit transition frequency lies in the 600–750 MHz range. Low frequencies lead to operation in a relatively hot environment. To initialize the qubit in the ground state, before each measurement, we employ a reset flux pulse that rapidly tunes the qubit frequency to several GHz. At this higher frequency, the thermal equilibrium corresponds to negligible excited state occupation. The circuit was fabricated by using the aluminum shadow evaporation process and allows to implement resource-efficient qubit control (qubit biasing and excitation are performed via the same control line) with a single arbitrary waveform generator (AWG) channel per qubit. Each qubit is driven directly by the AWG device, without any need for IQ mixers and high-frequency local oscillators. We demonstrate suppression of static ZZ interaction by using our tunable coupler design and achieve average single-qubit gate fidelities above 99.96% using Gaussian excitation pulses with 13.3 ns duration. The realized 60-ns-long two-qubit parametric-resonance fSim-type gate²⁹ demonstrates 99.55 ± 0.04% fidelity in cross-entropy benchmarking (XEB)⁷. We construct a 183.3-ns-long pulse sequence that implements the CZ gate with 99.23 ± 0.04% fidelity. The CZ pulse sequence consists of two fSim gates and five single-qubit gates and uses a spin-echo technique to compensate for the conditional phase accumulation during one fSim gate and transform the fSIMs swap angle into conditional phase rotation for CZ implementation.

Fig. 1: The fluxonium-based two-qubit quantum processor.

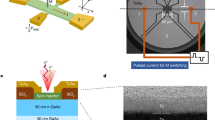
a Schematic diagram of an interacting three-body system. b Experimental realization of three capacitively coupled fluxonium-like qubits fabricated on a silicon substrate. c Circuit schematic. In b, false colors (blue, purple, green, orange, yellow, and red) are used to indicate the corresponding circuit components in d. 50 Ω terminators are installed at the 10 mK stage of the dilution refrigerator and used for qubits initialization (see Supplementary Fig. 1 for details).

Results

Device description

The two-qubit quantum processor consists of three capacitively coupled fluxonium circuits with additional harmonic modes, see Fig. 1a. An optical image of the processor chip is shown in Fig. 1b. The lowest two energy levels of the fluxonium modes of the left and right circuits A and B are used as data qubits. The middle circuit C is a two-mode tunable coupler, and is designed to always remain in the ground state. This scheme allows to realize a fSim-type gates^7,9.

The electric schematic of the two-qubit system is shown in Fig. 1c. The Hamiltonian of the system can be written as:

$${\hat{H}}_{{{{\rm{full}}}}}=\mathop{\sum}\limits_{i={f}_{{{{\rm{A}}}}},{f}_{{{{\rm{B}}}}},{f}_{{{{\rm{C}}}}}}{\hat{H}}_{i}+\mathop{\sum}\limits_{j={h}_{{{{\rm{A}}}}},{h}_{{{{\rm{B}}}}},{h}_{{{{\rm{C}}}}}}{\hat{H}}_{j}+\mathop{\sum}\limits_{ij}{\hat{g}}_{ij}.$$

(1)

The fluxonium (f_C) and harmonic (h_C) modes of the coupler at the center mediate the interaction between two distant fluxonium qubits (f_A and f_B). Transition frequencies of qubit A (Q_A) ω_A/2π and qubit B (Q_B) ω_B/2π at their flux degeneracy points are equal to 688.224 and 664.763 MHz, respectively, and can be tuned up to 3 GHz by applying an external magnetic flux through their loops. The measured coherence times of the qubits at the flux degeneracy point are T_1,A = 87 μs, T_1,B = 86 μs, T_2,A = 51 μs, T_2,B = 46 μs, ${T}_{2,{{{\rm{A}}}}}^{{{{\rm{E}}}}}=107\,{{{\rm{\mu s}}}}$, ${T}_{2,{{{\rm{B}}}}}^{{{{\rm{E}}}}}=93\,{{{\rm{\mu s}}}}$. More details about the device are provided in Supplementary Table 1. The harmonic mode frequency of the coupler (h_C) is ω_hC/2π = 2.0 GHz. The frequency of the coupler fluxonium mode (C_F) ω_CF/2π is tunable, similar to the qubits. Qubits and coupler frequencies are controlled via individual galvanically coupled fast flux bias lines.

As described in ref. ²⁸, after eliminating the coupler degrees of freedom and harmonic modes (h_A, h_B), our two-qubit processor obeys the effective low-energy Hamiltonian:

$${\hat{H}}_{{{{\rm{eff}}}}}/\hslash =-\frac{1}{2}{\omega }_{{{{\rm{A}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{z}}}}}-\frac{1}{2}{\omega }_{{{{\rm{B}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{z}}}}}+{g}_{{{{\rm{xx}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{x}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{x}}}}}+\frac{1}{4}{\zeta }_{{{{\rm{zz}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{z}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{z}}}}}.$$

(2)

Single-qubit gates via direct RF synthesis

We realize single-qubit gates and individual frequency control via a single flux bias line to each qubit. This approach has been recently demonstrated for transmon qubits^7,30. We use a Zurich Instruments HDAWG8 Arbitrary Waveform Generator (AWG), which has a 2.4 GHz sampling rate. In contrast to transmon qubits, where the frequency range of frequency control pulses is far apart from the frequency range required for qubit excitation, for fluxonium qubits, both DC signals and qubit frequency signals can be generated from a single AWG channel.

A common issue for flux control lines in superconducting qubits is attenuation and filtering: to access the full range of tunability of a superconducting qubit, one needs to be able to induce at least half of a magnetic flux quantum in the qubit loop. If the mutual inductance between the control line and the qubit is small, a large current amplitude in the control line is required. If the mutual inductance is large, the control line becomes a significant decay channel for the qubit excited state. The design value of the mutual inductance in our fluxonium circuits is 12 pH, which corresponds to a qubit lifetime of 1 ms²⁸ and bias current of 83 μA to shift the qubit into the flux degeneracy point. At the same time, the qubit drive Ω rate per unit AC current is Ω/I ≈ 320 MHz/μA.

We use the small excitation amplitude regime for single-qubit gate operation Ω ≪ ω. In this regime, the rotating wave approximation is valid. However, the excitation pulse amplitude is still sufficient to significantly shift the qubit from the flux degeneracy point, and counter-rotating terms in the Hamiltonian slightly shift the qubit frequency during the microwave pulses, resulting in phase errors. Our estimates for the average frequency shifts of the qubits due to these processes are 3.4 MHz and 0.7 MHz for a π/2-pulse, respectively. We use two different approaches to overcome these phase errors. Our first approach is based on the derivative removal by the adiabatic gate (DRAG) technique³¹. The excitation signal is given by

$$\begin{array}{l}{{\Omega }}(t)={\epsilon }_{x}(t)\sin \omega t+\alpha {\dot{\epsilon }}_{x}(t)\cos \omega t,\\ {\epsilon }_{x}(t)=A\left({e}^{-\frac{{t}^{2}}{2{\sigma }^{2}}}-{e}^{-\frac{{T}_{{{{\rm{p}}}}}^{2}}{2{\sigma }^{2}}}\right).\end{array}$$

(3)

We pick T_p = 13.3 ns, which corresponds to the minimum waveform length of the AWG, and σ = 3.3 ns. Even though the nature of phase errors in fluxonium qubits is very different from phase errors in transmon qubits, adding an extra signal into the orthogonal quadrature can remove the effect of the frequency shift to the first order. Using a sequence of calibration measurements, we find the values of A corresponding to π/2 and π pulses. Using a procedure based on the amplified phase error technique³², we find α.

The other approach to solving the phase error problem is virtual Z-gates³³. Here we only use one quadrature for the π/2-pulse, and correct for the phase error by adding a phase increment to the AWG’s numerically controlled oscillator (NCO). The phase increment is instant, and thus the Z-gate has unit fidelity. All single-qubit gates can be divided into three families: virtual Z-gates, denoted as U₁(φ), gates consisting of one π/2-pulse and a two Z-gates U₂(φ, λ), and all other single-qubit gates U₃(θ, φ, λ), which require two π/2 gates and three Z-gates.

We use the DRAG approach to demonstrate the high gate fidelities accessible to our two-qubit device. For all other measurements in this paper, we use the Z-gate approach, because it can be efficiently implemented in the native instructions of the AWG sequencer in a manner that is compatible with our reset pulse.

Measurement of single-qubit gate fidelity is carried out by Clifford-based randomized benchmarking (RB)^34,35,36. The Clifford group is generated from an identity pulse, a π/2-pulse, a π-pulse, and a virtual Z-gate that corresponds to a π/2 rotation. Among different decompositions of Clifford group gates, we pick the decomposition that has minimal duration, yielding an average of 5/6 13.3-ns-long pulses per gate. The results of single-qubit RB are shown in Fig. 2. We repeat the experiment for qubit A, qubit B, and qubit A and B simultaneously. The average Clifford group gate fidelities drop from 99.980 to 99.969% when switching from separate qubit benchmarking to simultaneous benchmarking for qubit A, and from 99.977 to 99.970% for qubit B. We attribute this degradation to residual σ^xσ^x coupling between the qubits when the coupling is turned off.

Fig. 2: Experimental results of randomized benchmarking for single-qubit gates on qubit A and qubit B.

a Measurement data of single-qubit RB for qubit A. b Measurement data of single-qubit RB for qubit B. “I” denotes the isolated application of single-qubit Cliffords and isolated qubit readout. “S” denotes the simultaneous application of single-qubit Cliffords and joint-qubit readout. Error estimates for fidelity are obtained from the least square fit errors. The data were averaged over 20 random sequences for each sequence length.

Two-qubit gates using a tunable coupler

Our two-qubit device allows to implement universal two-qubit gates from the fSim family^7,9, which describes the set of excitation number-preserving quantum logic operations on two qubits up to single-qubit phase rotations. Its matrix representation in the $\left|00\right\rangle$, $\left|01\right\rangle$, $\left|10\right\rangle$, $\left|11\right\rangle$ basis is given by:

$${{{\rm{fSim}}}}(\theta ,\varphi )=\left(\begin{array}{llll}1&0&0&0\\ 0&\cos \theta &-i\sin \theta &0\\ 0&-i\sin \theta &\cos \theta &0\\ 0&0&0&{e}^{-i\varphi }\end{array}\right),$$

(4)

where θ is the swap angle, and φ is the conditional phase.

We use the notation $\left|{Q}_{{{{\rm{A}}}}},{Q}_{{{{\rm{B}}}}}\right\rangle$ to represent the eigenstates of the system in the idling configuration when C_F is placed at its maximum frequency (${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}=0$) such that the effective qubit-qubit coupling is close to zero. Both qubits are parked at their minimal frequencies while idling and during single-qubit gates.

To experimentally characterize the dependence of ζ_zz on the coupler flux bias, we use an echo-like pulse sequence shown in Fig. 3a. The echo experiment is performed on qubit B. Parallel to the time reversal π pulse applied to qubit B, we can excite qubit A. After the reversal pulse, we apply a flux bias pulse to the coupler. Additionally, we introduce an additional phase shift to the final π/2-pulse that is proportional to the delay time, so that even without a flux pulse, we obtain 1 MHz oscillation. Both the coupler flux pulse and the excitation pulse applied to qubit A lead to frequency shifts of qubit B, changing the oscillation frequency. The measurement results are shown in Fig. 3b–d. The doubled frequency difference between the oscillation for excited and deexcited qubit A yields the ZZ interaction strength shown in Fig. 3e.

Fig. 3: Measurement of ZZ interaction strength ζ_zz.

a Pulse sequence of an echo-type experiment on qubit B while initializing qubit A in its ground (preparation gate I) or exited (preparation gate X_π) state. The final π/2-pulse phase is modulated proportionally to the delay. b Qubit B population measurement results without the π pulse applied to qubit A. c Qubit B population measurement results with the π pulse applied to qubit A. d Frequency of qubit B echo-type oscillations as a function of the coupler magnetic flux ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$. The blue curve corresponds to no excitation of qubit A and the green curve to excitation of qubit A in parallel to the π pulse applied to qubit B. e ZZ interaction strength ζ_zz as a function of ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$. The inset shows ζ_zz values near the zero flux point in the coupler.

The measurement results confirm that in our processor, the static ZZ interaction ζ_zz is nearly eliminated (less than 1 kHz) over a wide range of the magnetic fluxes in the coupler loop.

We aim at implementing an $\sqrt{{{{\rm{iSWAP}}}}}$-like gate by diabatically inducing vacuum Rabi oscillations between the $\left|10\right\rangle$ and $\left|01\right\rangle$ states. The oscillation rate is controlled by adjusting ω_CF, which effectively tunes the coupling strength g_xx [Fig. 4c].

Fig. 4: Effective XX coupling strength as a function of coupler flux.

a Pulse sequence to measure qubit-qubit coupling under modulation (qubit B tuned in resonance with qubit A) as a function of the coupler flux bias. b Experimental data for the energy exchange between $\left|10\right\rangle$ and $\left|01\right\rangle$, as a function of the magnetic flux in the coupler ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$. c The effective qubit-qubit coupling g_xx versus ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$.

The frequency difference between the qubits in their working points is approximately Δ/2π = 23 MHz, while the maximum effective coupling strength is around ${g}_{{{{\rm{xx}}}}}^{\max }/2\pi \approx 8\,{{{\rm{MHz}}}}$. Due to the large detuning, ramping up the effective coupling strength between the qubits alone is insufficient to realize an $\sqrt{{{{\rm{iSWAP}}}}}$ gate: the vacuum Rabi oscillation amplitude, estimated by the formula $4{g}_{{{{\rm{xx}}}}}^{2}/(4{g}_{{{{\rm{xx}}}}}^{2}+{{{\Delta }}}^{2})$, yields a maximum population transfer of 0.33 from the $\left|01\right\rangle$ state into the $\left|10\right\rangle$ state, while the $\sqrt{{{{\rm{iSWAP}}}}}$ implies a 0.5 population transfer.

The straightforward solution to the frequency detuning problem is to apply a flux pulse to qubit B’s control line simultaneously with the flux pulse to the coupler. However, this approach undermines the very idea of using a fluxonium qubit for higher coherence due to the large dephasing rates of superconducting qubits outside of flux sweet spots.

To overcome this obstacle, we employ the parametric frequency shift technique introduced for transmon qubits in²⁹. Instead of applying a rectangular-shaped flux pulse to the qubit, the frequency is shifted with an AC signal. This significantly reduces the impact of low-frequency flux noise on qubit coherence. The amplitude of this modulation is chosen so that the effective frequency of qubit B becomes equal to qubit A’s frequency. The calibration procedure for the parametric frequency shift pulse is described in Supplementary Note III.

Gate calibration

We first characterize the effective qubit-qubit coupling strength g_xx by measuring the energy exchange between $\left|10\right\rangle$ and $\left|01\right\rangle$ states as a function of the coupler flux bias. To measure the energy exchange, we prepare the $\left|01\right\rangle$ state by applying a π-pulse to qubit B followed by a modulated flux pulse Φ_B(t) (frequency ω_p/2π = 100 MHz, amplitude $\tilde{{{\Phi }}}=0.016\,{{{\Phi }}}_{0}$) to bring it into resonance with qubit A for a variable pulse duration t_d [Fig. 4a]. During the parametric modulation, we vary the effective qubit-qubit coupling strength by biasing the coupler flux with a square-shaped flux pulse with amplitude ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$. The populations of the qubits are measured as a function of t_d and ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ [Fig. 4b].

To quantify the qubit-qubit coupling strength g_xx we fit the oscillations of the $\left|01\right\rangle$ state population with harmonic oscillations at every coupler flux offset. The frequencies of the fitted harmonic oscillations are shown in Fig. 4c. As expected from the simulations²⁸, the maximum value of coupling strength occurs at the flux degeneracy point of the coupler (Φ_C = 0.5Φ₀) and it also stays relatively constant g_xx/2π ≈ 0.4MHz in a range from −0.3Φ₀ to 0.3Φ₀.

fSim metrology

Here we consider an $\sqrt{{{{\rm{iSWAP}}}}}$-like gate, ${{{\rm{fSim}}}}(\theta ,\varphi )$ with θ = −π/4. The gate consists of a parametric frequency shift pulse applied to qubit B and a flux pulse to the coupler. The total gate duration is 60 ns, which corresponds to six periods of the parametric frequency shift signal. To avoid leakage outside the computational subspace, we replace the front and back edges of the coupler flux pulses with fragments of a sine wave. The edge times are chosen such that the gate amplitude is as close to 0.5Φ₀ as possible, resulting in 14 ns for both front and back edges. After the amplitude calibration procedure (described in Supplementary Note V), we obtain a pulse amplitude of 0.49787Φ₀.

To verify the fidelity of the fSim gate, we use cross-entropy benchmarking (XEB), described in detail in ref. ⁷. The main feature of the method is that it allows not only to evaluate the accuracy of a target gate, but also to estimate unknown parameters in the gate unitary matrix. Apart from the θ and φ angles explicitly identified in the ${{{\rm{fSim}}}}$ definition (4), our gate also includes three independent single-qubit phase rotations.

Another important issue is that the frame of the XX coupling, which generates the ${{{\rm{fSim}}}}$ gate, is distinct from the single-qubit gate frames. The relative phase of the NCOs used for single-qubit unitaries depends on time as $\left({\omega }_{{{{\rm{A}}}}}-{\omega }_{{{{\rm{B}}}}}\right)t$; this phase also enters the non-diagonal matrix elements of the unitary matrix. Similarly, virtual Z-gates implemented by phase shifts of the NCOs have no effect on the ${{{\rm{fSim}}}}$ gate. Thus, effectively we have two relevant frames describing the device: the single-qubit rotation frame, which is defined by the oscillators in waveform generators controlling the qubits, and the laboratory frame, where the qubits rotate at different frequencies. Simulations of the system evolution under both single-qubit and ${{{\rm{fSim}}}}$ gates must account for the frame changes.

The idea of the XEB method is similar to randomized benchmarking (RB) and interleaved randomized benchmarking (IRB). Unlike in RB and IRB, after executing a sequence of random gates we do not apply a cancellation gate that returns the qubit into an eigenstate of the measurement operator, but measure the system in a random superposition state. For each circuit depth (m), measurements are performed for a large number (100) of different random sequences.

The gate parameter estimation is performed by comparing the measured probability distributions with probability distributions simulated for sequences of ideal unitary gates. By maximizing linear cross-entropy between simulation and experiment, we obtain estimates for the gate parameters: θ/π = 0.2502, φ/π = 0.0255. After finding the unitary gate parameters, we estimate the average depolarization fidelity of the final state $\overline{{\varepsilon }_{m}}$. It can be approximated by the function ap^m, where p is the depolarizing parameter and a is fitting parameter used to account for state preparation and measurement (SPAM) errors. The average fidelity of the executed gates is given by

$$F=p+(1-p)/D,$$

(5)

where D = 2ⁿ is the dimension of the Hilbert space (n = 2). If a target gate is inserted after each single-qubit operation, the average fidelity of the gate is determined by the formula (5) with p = p₂/p₁, where p₂ and p₁ are the depolarizing parameters corresponding to the gate sequences with and without (reference sequences) the interleaved gate.

In Fig. 5b, the blue dots show the exponential decay of the depolarization fidelity $\overline{{\varepsilon }_{m}}$ of the reference random single-qubit Clifford-gate sequences executed simultaneously on two qubits. The green dots show similar data when an fSim gate is inserted between single-qubit operations, as shown in Fig. 5a. From a least squares fit we obtain p₁ = (99.697 ± 0.016)% and p₂ = (99.10 ± 0.04)%. The resulting fidelity of the fSim gate is F = (99.55 ± 0.04)%.

Fig. 5: Cross-entropy benchmarking (XEB) of the $\sqrt{{{{\rm{iSWAP}}}}}$-like gate.

a Pulse sequence for the XEB experiment. b Depolarization fidelity for the reference circuits and interleaved circuits.

CZ gate calibration and metrology

The ${{{\rm{fSim}}}}$ gate that can be naturally implemented in our two-qubit device has a number of drawbacks. Firstly, it is the issue of two different frames for single-qubit gates and two-qubit gates that is discussed above. Secondly, an entangling Clifford group two-qubit gate, such as iSWAP or CZ, would be more helpful to compare the performance of our device with other two-qubit gate implementations. Finally, Clifford group two-qubit gates have the advantage of being the primitive used in many algorithms.

To resolve these problems, we construct a CZ gate from two ${{{\rm{fSim}}}}(\frac{\pi }{4},\varphi )$ gates and five single-qubit gates, using the sequence proposed in the Supplementary Fig. 7 of ref. ²⁸. The sequence is shown in terms of pulses applied to different control channels in Fig. 6a. At the core of this pulse sequence lie two identical ${{{\rm{fSim}}}}$ gates interleaved by a π-pulse, denoted as U₃(π, φ_x, λ_x − φ_x). This echo-like sequence cancels out the conditional phase accumulation φ in the ${{{\rm{fSim}}}}$ gates. The resulting gate is up to single-qubit gates equivalent to CZ. Furthermore, it can be shown that these single-qubit gates can be expressed in terms of π/2 pulses, denoted as U₂(φ_i, λ_i − φ_i), i ∈ {1, 2, 3, 4}.

Fig. 6: Controlled-Z-gate calibration and quantum process tomography results.

a Gate sequence equivalent to CZ. b–e Calibration data for φ₁, φ₂, φ₃, φ₄ (blue dots), and approximation with a cosine function. f Pauli transfer matrix of the calibrated CZ gate (on the left) with fidelity 99.4% obtained from quantum process tomography. Pauli transfer matrix of the ideal CZ gate (on the right) is shown for comparison.

A further key premise of this sequence is that the CZ operator is diagonal in the computational basis. Thus, it remains invariant under the unitary transform connecting the single-qubit gate frame and the two-qubit gate frame. Once we construct a pulse sequence in the laboratory frame that implements CZ, this pulse sequence can be used at any point in time. Unlike the pulses used to implement standalone single-qubit gates, the single-qubit gates in this sequence should always have the same modulation phase in the laboratory frame. This ensures that the relative phase between the ${{{\rm{fSim}}}}$ gate and the single-qubit gates remains the same.

The CZ calibration procedure starts with a known π/2 single-qubit gate pulse amplitude and a known pulse sequence corresponding to ${{{\rm{fSim}}}}(\pi /4,\varphi )$. We require no prior knowledge about the relative phases of either of these pulses. Let U be the unitary matrix describing the action of the pulses shown in Fig. 6a. For any values of relative phases λ₁, λ₂, λ₃, λ₄, λ_x, φ_x, there exists a set of values φ₁, φ₂, φ₃, φ₄ for which U is diagonal. Furthermore, the squared absolute values of the diagonal entries of U can be expressed as

$$| {u}_{ii}{| }^{2}=\mathop{\prod }\limits_{j=1}^{4}{\cos }^{2}\frac{{\varphi }_{j}-{\varphi }_{j}^{o}}{2},$$

(6)

where ${\varphi }_{j}^{o}$ correspond to the sought-after values of φ_j which correspond to a diagonal unitary U.

We probe the sum of the squared absolute values of the diagonal entries of U by preparing each of the computational states, performing the gate sequence, and measuring the population retained in the prepared state. This resulting quantity can be interpreted as the trace of the classical transition probability matrix. Note that according to equation (6), all the diagonal entries of the transition probability matrix are equal, and are products of functions of φ₁, φ₂, φ₃, and φ₄. Therefore, the values ${\varphi }_{1}^{o}$, ${\varphi }_{2}^{o}$, ${\varphi }_{3}^{o}$, and ${\varphi }_{4}^{o}$ can be found using only single-dimensional scans over φ₁, φ₂, φ₃, and φ₄. The measured transition probability matrix traces are shown in Fig. 6b–e.

After obtaining a pulse sequence that corresponds to a diagonal operator that is up to single-qubit operations equivalent to the CZ gate, there are only two free parameters. These parameters are the angles of single-qubit rotations around the Z-axis. We determine these angles by quantum process tomography. After supplementing the pulse sequence with virtual Z-rotations to revert these rotations, we repeat the process of tomography. The resulting Pauli transfer matrix is shown in Fig. 6f, and the gate fidelity obtained from this measurement is 99.4%.

Finally, we estimate the fidelity of the CZ gate by iterative XEB. The quantum circuit of the experiment is shown in Fig. 7a. The experiment is performed for n sequential CZ gates interleaved with random single-qubit Clifford gates. Figure 7b,c shows the depth dependence of the average depolarization fidelity. The obtained fidelity of the iterated CZ gates varies linearly with their number, which indicates the absence of coherent errors. From a linear fit, we obtain a gate fidelity of F = (99.22 ± 0.03)% per single gate. The errors are obtained by the standard variance of the least squares method and conventional formulas for calculating errors.

Fig. 7: XEB for the CZ gate.

a Pulse sequence for the XEB experiment with the CZ gate. b XEB results of the CZ gate. We use a variable number of CZ gates (up to 4) (encoded in color) between the randomly chosen Clifford gates. For each circuit depth, we average over 100 sequences. c Fidelity of CZⁿ versus n. Linear dependence indicates incoherent errors.

Discussion

We have demonstrated a two-qubit quantum processor based on the modified fluxonium qubits in a tunable coupler architecture and realized high-fidelity fSim and CZ gates on the same device. To implement two-qubit gates, we used a parametric flux modulation to bring the qubits into resonance with each other. As our qubits have low transition frequencies, here we also proposed and implemented an unconditional reset mechanism for qubits initialization. The tunable coupling scheme helped us to obtain high-fidelity two-qubit operations and suppress residual ZZ-coupling rate (here less than 1 kHz), allowing for parallel high-fidelity single-qubit operations.

Taken together, this work reveals an interesting and promising approach towards fault-tolerant quantum computing with low-frequency qubits that can be a good alternative and competitive to the transmon system. We believe that the low frequency of data qubits opens the possibility of using sub-gigahertz wiring and electronics for gate operations and individual qubit control, which in turn allows to reduce the complexity of the control system via using a single flux bias line for each qubit.

Methods

Device design and fabrication

The design of the investigated system consists of the tunable two-qubit quantum processor (lower part of the chip in Fig. 8a) and a single-qubit (Q_S) (upper part of the chip in Fig. 8a), which is also implemented as a two-mode fluxonium circuit, and is used for test measurements.

Fig. 8: The fluxonium-based device.

a The optical image of the chip. b The optical image of two qubits and coupler. c SEM images of the fluxonium device, magnified image of the junctions array of the qubit A, and the single junction.

The device is made in a four-step process: (I) Base Al layer patterning, (II) Josephson junction double-angle evaporation and lift-off, (III) patterning and deposition of bandages, and (IV) crossovers fabrication.

Devices are fabricated on Topsil Global Wafer’s high-resistivity silicon substrate (ρ > 10,000 Ohm cm, 525 μm thick). Prior to the deposition, the substrate is cleaned in a Piranha solution at 80 ^∘C, followed by dipping in a 2% hydrofluoric bath to remove the native oxide. A 100-nm-thick base aluminum layer is grown using e-beam evaporation in an ultra-high vacuum deposition system. A 600-nm-thick Dow MEGAPOSIT SPR 955-CM photoresist is then spin-coated. Qubit capacitors, resonators, wiring, and ground plane are defined using a laser direct-writing lithography system (Heidelberg Instruments uPG 101), developed in AZ Developer to minimize film damage and then dry etched in BCl3/Cl2 inductively coupled plasma (Oxford PlasmaPro100). The photoresist is stripped in N-methyl-2-pyrrolidone at 80 ^∘C for 3 h and rinsed in IPA (isopropyl alcohol) with sonication.

The substrate is then spin-coated with a resist bilayer composed of 500 nm MMA (methyl methacrylate) and 300 nm PMMA (poly methyl methacrylate). The development is performed in a bath of MIBK/IPA 1:3 solution followed by a rinse in IPA. Al/AlOx/Al Josephson junctions are patterned using an electron beam lithography system (Raith Voyager) and aluminum electrodes are shadow-evaporated in an ultra-high vacuum deposition system. A 25-nm-thick first Al junction electrode is oxidized at 5 mbar to form the tunnel barrier, and next, the 45-nm-thick counter-electrode is evaporated. We then pattern and evaporate aluminum bandages using the same process as for junctions with an in situ Ar ion milling in order to provide good electrical contact of the junction with the base layer. Lift-off is performed in a bath of N-methyl-2-pyrrolidone with sonication at 80 ^∘C for 3 h and rinsed in a bath of IPA with sonication.

Finally, aluminum free-standing crossovers are fabricated using a conventional approach³⁷. SPR 220 3 um photoresist is spin-coated and then the sacrificial layer is patterned using a direct laser writing system. The development is performed in AZ Developer/deionized water solution (1:1) for 2 min in order to minimize film damage, and the resist is reflowed at 140 ^∘C. A 300 nm of Al is then evaporated with an in situ Ar ion milling to remove the native oxide. The second layer of 3 um SPR 220 is used as a protective mask and the excess metal is dry etched in inductively coupled plasma. A damaged layer of photoresist is then removed in oxygen plasma and both layers of photoresist are stripped of N-methyl-2-pyrrolidone at 80^∘C.

Experimental setup

The experiments are performed in a BlueFors LD-250 dilution refrigerator with a base temperature of 10 mK, as shown in Fig. 9. The chip is connected to the control setup with eight lines: the readout line, three lines for simultaneous single-qubit gates application (XY controls) and flux control (Z control), three lines connected with 10 mK stage and ended with 50 Ω terminators for qubit reset, and the coupler’s control line for two-qubit gates.

Fig. 9: Schematic diagram of the experimental setup.

Single-qubit control pulses modulated with qubit frequencies, flux offsets, and two-qubit gates applied to the coupler are generated directly using one analog output port of the arbitrary waveform generator.

Pulse generation and flux control are fully performed by a Zurich Instruments HDAWG8 arbitrary waveform generator. One analog output port of the generator is used per fluxonium circuit. IQ microwave mixers are employed to up- and downconvert the intermediate-frequency readout pulses to the resonator frequencies and back. After getting reflected from the qubit chip, the readout microwave signal is measured by a vector network analyzer (R&S ZVB20) for spectroscopy and a home-built digitizer setup for single-shot readout. For mixer calibration, we use a spectrum analyzer (Agilent N9030A).

Microwave attenuators are used to isolate the qubit chip from thermal and instrumental noise from the signal sources, which are located at room temperature. The readout line is equipped with an impedance-matched parametric amplifier (IMPA) followed by a Quinstar CWJ1019KS414 isolator to prevent noise from higher-temperature stages entering the IMPA and the qubit device. We pump the IMPA using an Agilent E8257D signal generator. Three Raditec RADC-4.0-8.0-Cryo circulators and a set of low-pass and high-pass filters placed after the sample allow for the signal to pass through to the IMPA without being attenuated while removing all the reflected noise of the IMPA and dumping it into a 50Ω termination. At the PT2 stage (3 K) of the cryostat, an LNF-LNC0.3_14A high electron mobility transistor (HEMT) is installed. The output line is further amplified outside the cryostat with two Mini-Circuits ZVA-183-S+ amplifiers.

Due to the large DC control current of ~83 μA required for qubit biasing, reset pulses, and control, we cannot install attenuators on the 10 mK stage of the cryostat to suppress thermal noise from room temperature microwave sources. Instead, we use a low-pass filter (Mini-Circuits VLF-630+) in combination with a powder filter with 15 dB attenuation close to the qubit frequencies. Capacitively coupled qubit control lines are connected to 50 Ω terminators at the 10 mK stage of the cryostat. Due to the low capacitive coupling, these lines have no effect when the qubit frequency is low, but result in enhanced decay when the bias flux is close to zero. This effect is used for qubit initialization and reset (see Supplementary Fig. 1).