A quantum router architecture for high-fidelity entanglement flows in quantum networks

Abstract

The past decade has seen tremendous progress in experimentally realizing the building blocks of quantum repeaters. Repeater architectures with multiplexed quantum memories have been proposed to increase entanglement distribution rates, but an open challenge is to maintain entanglement fidelity over long-distance links. Here, we address this with a quantum router architecture comprising many quantum memories connected in a photonic switchboard to broker entanglement flows across quantum networks. We compute the rate and fidelity of entanglement distribution under this architecture using an event-based simulator, finding that the router improves the entanglement fidelity as multiplexing depth increases without a significant drop in the entanglement distribution rate. Specifically, the router permits channel-loss-invariant fidelity, i.e. the same fidelity achievable with lossless links. Furthermore, this scheme automatically prioritizes entanglement flows across the full network without requiring global network information. The proposed architecture uses present-day photonic technology, opening a path to near-term deployable multi-node quantum networks.

Introduction

Quantum networks distribute quantum information to enable functions that are impossible on classical networks. Key to these applications is the sharing of entanglement between many users over large distances, allowing quantum key distribution, distributed quantum computing, and quantum-enhanced sensing. While entanglement distribution has been demonstrated over short distances¹, long-distance quantum networking is hampered by the exponential loss of photons in optical fibers². Quantum repeaters³ can overcome this problem by forming chains of entangled nodes.

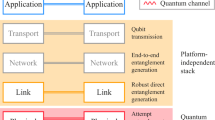
Figure 1a shows a schematic of such a repeater-connected quantum network. A graph of quantum repeaters connected by quantum links forms the backbone of the network. Client nodes are quantum computers that connect to the network through their nearest repeater node, while repeater nodes facilitate the sharing of entanglement between clients. Hidden under the link-layer abstraction⁴ lies a physical layer of repeater devices and lossy quantum channels, the components of which are illustrated in the Figure. A typical repeater device, shown in Fig. 1b, consists of memory capable of generating and storing entanglement with a photonic mode. The entanglement scheme used in a link between two repeater nodes determines the devices and channels used in the physical layer. Nitrogen vacancy (NV) centers in diamond have been entangled at a distance of 1.3 km¹ using the emission-based scheme proposed by Barrett and Kok⁵, which uses a 50:50 beamsplitter to erase which-path information and detectors to herald entanglement. A related scheme proposed by Cabrillo⁶ was used to provide on-demand entanglement between NV centers using a phase-stabilized fiber link⁷. Recently, the direct-transmission (PLOB) bound² for quantum communication was broken⁸ using a scheme proposed by Duan and Kimble⁹, which relies on scattering photons from spins in high-cooperativity cavities. These protocols are all inherently probabilistic, such that a single attempt at distributing entanglement succeeds with probability p_distant.

Fig. 1: Components of a quantum repeater network.

The quantum network comprises client nodes, which end users directly access, and repeater nodes, which connect clients by propagating entanglement through the network. a Physical layer implementation. In the physical layer⁴, repeater nodes may be connected by a variety of entanglement protocols. While all protocols require transmission of an entangled photon through a photonic channel, the specific protocol used in each link determines the physical configuration of these channels (e.g. optical fibers) and measurement devices associated with that link. Possible protocols include the cavity-mediated Duan–Kimble protocol⁹ and the photon emission-based Barrett–Kok⁵ and Cabrillo⁶ protocols. These latter protocols employ an intermediate detector station between nodes to herald successful entanglement. b Components in a repeater node. We classify repeater nodes based on the number of other nodes they connect to: a 4-way and a 3-way repeater are labeled. All adjacent repeater nodes are connected by quantum and classical channels (shown explicitly in black and light red respectively). c Detector station used in the photon emission-based protocols to herald entanglement.

The latency due to two-way communication for entanglement distribution in first-generation repeater networks forms a bottleneck that can be resolved by multiplexing many quantum memories at each repeater node¹⁰. To overcome this problem of latency, ref. ¹¹ introduced a multiplexing scheme that is restricted to cavity-based entanglement protocols. Alternatively, ref. ¹² proposed a scheme that is compatible with emission-based protocols but does not maintain the fidelity of entanglement distribution. Previous papers considered switching to improve quantum key distribution rates, but have not quantified the effects of local connectivity on infidelities^13,14,15. Here, we introduce a quantum router scheme that uses multiplexing and all-to-all conditional local switching to increase entanglement fidelities and maintain entanglement rates for leading memory types and entanglement protocols. Our router architecture bears similarities to the quantum key distribution protocol introduced in a contemporaneous proposal by Trényi and Lütkenhaus¹⁶, but our paper considers spin-photon implementations of quantum repeaters in general quantum networks.

The router uses local, low-loss connections to link different users’ entangled qubits, thereby establishing entanglement across the channel. This quantum router architecture is motivated by recent advances in integrated photonics, with demonstrations of fast and low-loss on-chip switching¹⁷ of many photonic modes and the integration of quantum emitters with integrated circuits¹⁸.

In comparison with previous works, our proposed quantum router architecture is compatible with any entanglement generation protocol and quantum memory in the physical layer. Furthermore, our architecture extends naturally to chains of routers; in fact, we show that if brokered entanglement is used, the router can redirect entanglement flows to minimize latencies using only local information. We demonstrate these benefits by comparing the router architecture with a standard multiplexed architecture in which entanglement between users is generated serially^19,20, exploring the various impacts on repeater performance.

Results

Router architecture

We analyze the performance of our quantum router architecture for the NV center in diamond as the qubit platform and the Barrett–Kok⁵ scheme as the entanglement protocol. However, our architecture is agnostic to the specific physical memory and entanglement-generation protocol.

In Fig. 2, we show the connectivity between photonic and stationary qubits in (a) a standard multiplexed repeater considered for diamond color centers¹⁹, and (b) a multiplexed repeater with a router. In this representation, each qubit register within the router is linked by a distinct mode to a corresponding register at an adjacent neighboring node, here labeled left and right for generality. Different modes are shown separately, though they may be transmitted through the same physical channel, for example via temporal or spectral multiplexing. Each qubit register comprises a single NV center with two physical qubits: one electron spin (dark red), which can be used for optically-mediated entanglement, and one nuclear spin (light red), which has no optical transition but which can use spin–spin interactions to couple to and store quantum information from its local electron spin. This enables the use of “brokered entanglement”²¹, where the electron spin serves as a short-term “broker” of entanglement to the longer-term “storage” qubit of the nuclear spin.

Fig. 2: Abstract representation of a 2-way standard repeater and a 2-way router in a quantum network.

Each repeater node hosts m qubit registers, each of which here is formed by an NV center in diamond comprising a optically active electron spin (dark red) coupled to a long-coherence nuclear spin (light red), where the former serves as a broker to store entanglement in the latter. Multiple optical modes can be transmitted through the same physical link, e.g., via temporal or spectral multiplexing. a Standard routerless repeater. In a standard repeater, each qubit register has lossy quantum links to registers at adjacent network nodes on both the left and the right. b Router. In our router architecture, each qubit register has lossy links to only one of the left or right neighbors; however, the repeater node contains local, low-loss quantum channels that enable entanglement generation between all registers in the left bank and all registers in the right bank. As a result, the mean time a storage qubit must idle t_idle while holding entanglement is shorter with a router. The idling time depends on t_distant (the network clock period), t_local (the local clock period), p_distant and p_local (the probability of generating entanglement over a distant and local link, respectively).

In the routerless architecture (Fig. 2a), each of the m qubit registers first establishes entanglement with the left neighboring node via its electron spin and the corresponding optical mode. Letting p_distant be the success probability of one entanglement generation attempt, the process takes an average number of attempts 1/p_distant. Once successful, this entanglement is swapped to the nuclear spin for storage, at which point the electron spin attempts to establish entanglement with the right neighbor, again requiring an average of 1/p_distant attempts. Thus, the nuclear spin must idle while storing entanglement for an average time t_idle ~ t_distant/p_distant, where t_distant is the time needed per attempt of the entanglement protocol, typically limited by the round-trip communication time between the repeater and a detector station. Once this succeeds, a Bell state measurement (BSM) on the joint electron-nuclear spin state teleports entanglement to be shared between the left and right nodes. This protocol is performed simultaneously and independently on each qubit register.

In contrast, our router architecture (Fig. 2b) defines two “banks” of registers, one with $\frac{m}{2}$ registers with optical links to the left, the other with $\frac{m}{2}$ registers with optical links to the right. The router connects these two banks using a low-loss $\frac{m}{2}\times \frac{m}{2}$ switchboard, over which entanglement protocols succeed with probability p_local ≫ p_distant. In this architecture, each qubit register first establishes entanglement with either the left or the right, as determined by their optical connectivity. As in the routerless case, each link requires an average of 1/p_distant attempts before succeeding, after which these “successful” registers will then swap entanglement to their nuclear spin. At this point, any successful registers enter a “pairing” stage where registers in opposite banks are paired up and subsequent clock cycles attempt entanglement between electron spins in these pairs. This requires an average number of attempts 1/p_local, taking a time t_idle ~ t_local/p_local; here, the local clock period t_local is likely dominated by any state initialization required by the entanglement protocol. Any successful but unpaired registers idle, waiting for a successful partner on the opposite side to become available. Once entanglement is formed within a pair, two electron-nuclear spin BSM’s—one at each register—teleport entanglement to be shared across the full left-right link.

Figure 3 compares the timeline of activity for a router and a standard repeater. Even though the router requires an additional “pairing” stage, this stage requires a negligible amount of time compared to the time needed for a distant entanglement attempt t_distant, so the router and the standard repeater can have similar clock cycles. Moreover, the router uses the entanglement with its neighboring nodes more quickly than the standard repeater does, so the router reaches its steady-state rate in a smaller number of clock cycles than the standard repeater.

Fig. 3: Timeline of activity for each memory in a standard repeater and a router, in the limit of high multiplexing (m → ∞).

Note that for visibility, here p_distant is set to 0.2, which is 250 × the value in our simulations. a The horizontal axis represents time—three router clock cycles are shown here—and the vertical axis represents the number of memories involved in each stage of entanglement generation. The different stages of entanglement generation are color-coded. Full left-right entanglements are represented by boxes, the height of which is the number of left-right entanglements and the length of which is the time from the first successful distant entanglement attempt to the formation of left-right entanglement. The idling time of the first distant entanglement is hatched. Both the standard repeater and router are initialized with no entanglement at time = 0 μs. The router has a significantly shorter idling time t_idle than the standard repeater. (See Supplementary Note 5 for more details.) b The horizontal axis represents time (on the same scale as in a), but the vertical axis represents the cumulative number of Alice–Bob entanglements generated at any given time.

This router architecture has two primary advantages even at steady state. First, the idling time t_idle that a storage qubit must hold entanglement can be greatly reduced, decreasing errors due to decoherence. Second, the number of entanglement attempts a register must make while its storage qubit holds entanglement is reduced by a factor p_local/p_distant, thus sharply reducing the storage-qubit decoherence due to broker-qubit entanglement attempts. In the remainder of this article, we quantitatively examine the impact the router has on the steady-state performance of a quantum network.

Simulations

We use the NetSquid discrete event simulator²² to compare the performance of repeaters with and without a router, computing the average rate and fidelity of entanglement distribution for a one-repeater network. In this network, a single repeater station connects Alice and Bob, as shown in Fig. 2 where Alice is the “left node” and Bob is the “right node.” We compare each architecture using the same number of total NV qubit registers m at the repeater, under the assumption that qubit registers will be a scarce resource in near-term quantum networks. We choose the emission-based Barrett–Kok protocol⁵ for our entanglement protocol. The physical parameters of our repeater memories correspond to a realization using photonic integrated circuits discussed below, using experimentally realized values reported in the literature (see Supplementary Note 1 for details).

Figure 4b plots the entanglement distribution rates for both repeater architectures for various link distances as a function of the number of qubit registers m at the repeater node. For the routerless case, the rate scales linearly with m since the qubit registers operate independently. For low m, the router exhibits comparatively lower rates; however, as m increases, the difference between the two protocols decreases, such that in the limit of large m the two architectures perform comparably. This difference can be attributed to mismatches in the number of successful entanglements in Alice’s and Bob’s banks after a given clock cycle. The delay in resolving these mismatches, the number of which scales with $\sqrt{m}$, lowers the rate of the router below the linear scaling of the routerless architecture. However, the fractional impact of this effect on the rate is reduced for large m, and the rate of the router approaches the routerless rate (see Supplementary Note 2 for a lower bound on the router rate).

Fig. 4: Simulation results for different repeater configurations.

Each data point is the result of three independent simulations. The average rates and infidelities are plotted, with the standard error of the mean shown as the error bars. The lengths (1, 10, 20, 30 km) refer to the distance L between the repeater node and the detector station. a Link layer representation of the simulated one-repeater network. b Steady-state entanglement rate against m. As expected, the rate of entanglement generation increases with the number of repeater qubit registers (m), as expected. The entanglement rate of the router architecture is slightly lower than the entanglement rate of the standard repeater, and the difference decreases as the size of the repeater increases. c Ratio of entanglement infidelity against m. The fidelity of entanglement generated by the router is higher than that of the standard repeater for sufficiently large distances L. The fidelity of entanglement generated by the router improves as m increases, whereas that of the standard repeater does not. This causes the infidelity ratio to decrease as m increases. d Router infidelity against m. As m increases, the router infidelity approaches a channel-loss-invariant value that only depends on local gate fidelities and the round-trip travel time.

Figure 4c, d plot the infidelity of the distributed entanglement for repeaters with and without a router. We consider three sources of infidelities in the distributed entanglement. The first source of infidelity is the typical depolarizing and dephasing noise experienced independently by the electron and nuclear spins, as characterized by their T₁ and T₂ coherence times. We model this noise on a qubit after time t as:

$$\rho =\left(\begin{array}{ll}1-{\rho }_{11}&{\rho }_{01}\\ {\rho }_{01}^{* }&{\rho }_{11}\end{array}\right)\mapsto \left(\begin{array}{ll}1-{\rho }_{11}{e}^{-t/{T}_{1}}&{\rho }_{01}{e}^{-t/{T}_{2}}\\ {\rho }_{01}^{* }{e}^{-t/{T}_{2}}&{\rho }_{11}{e}^{-t/{T}_{1}}\end{array}\right).$$

(1)

For a repeater with no router, adding additional registers does not affect the amount of time an individual register must store entanglement; thus, increased multiplexing does not reduce this decoherence channel. However, for a repeater with a router, the number of registers has a dramatic effect on the fidelity. This observation can be understood by considering the mean idling time for memory in this scheme, which is determined by the number of clock cycles a given register in the Alice (Bob) bank must idle after establishing entanglement on its respective side of the link before a register in the Bob (Alice) bank also succeeds and is available for the pairing stage of the protocol. This maps to the success mismatch problem discussed earlier; as such, in the limit of large m, most successful registers will be paired with a register in the opposite bank with every clock cycle, such that the idling time approaches the duration of a single such cycle. In contrast, with no router, a register must idle for on average 1/p_distant ≫ 1 cycles. Thus, the addition of a router reduces the infidelity from this channel by a factor that approaches p_distant.

The second source of error stems from the coupling between the nitrogen nuclear spin and the NV electron spin. In particular, each excitation of the electron spin used to generate spin-photon entanglement in the Barrett-Kok protocol generates noise that decoheres the qubit stored in the nuclear spin. We can model this interaction-induced noise on the nuclear spin as¹⁹:

$$\rho \mapsto (1-a-b)\rho +aZ\rho Z+b\frac{{\mathbb{I}}}{2},$$

(2)

where the dephasing a ≈ 1/4000 and the depolarization b ≈ 1/5000 for NV centers. Note that for other systems with stronger electron-nuclear spin coupling such as silicon-vacancy centers in diamond²³, this effect may be stronger. For both architectures, after a register has generated one entanglement link, it stores that entanglement in the nuclear spin while its electron spin attempts to generate entanglement on the other side—either directly to Bob in the case with no router, or to the opposite bank when using a router. In either case, each failed attempt decreases the fidelity of the final Alice-Bob EPR pair. Without a router, the mean number of failed attempts is equal to 1/p_distant; with a router, this number is instead 1/p_local, dramatically reducing the infidelity from this effect.

The third source of infidelity comes from imperfect two-qubit gates and electron spin readout. The proposed router needs to perform twice as many two-qubit gates and readouts for each distributed EPR pair as a standard repeater. The cumulative infidelity of these operations is independent of m, p_distant, and p_local. When the link between adjacent nodes is short, these operations dominate the infidelity of the Alice-Bob EPR pair, disadvantaging the router. However, when the link becomes lossier, the previous two sources of infidelity dominate, causing the router to increasingly outperform the standard repeater in entanglement fidelity (see Supplementary Note 3 for more details).

As a result, the router enables channel-loss-invariant entanglement fidelity; that is, regardless of the network link efficiency, the router can achieve fidelity that is limited only by the gates performed on the quantum memories and decoherence during a single round-trip transit of the network. A threshold is crossed as the number of entanglement attempts per clock cycle exceeds 1/p_distant, where the average clock cycle produces at least one entanglement event on both sides of the router. This limits the decoherence a memory must endure to that of one clock cycle, and, for the case where the memory coherence time is much longer than the link round-trip time, allows all routers to realize a fidelity that is purely limited by the fundamental gates necessary to perform the protocol (initialization, swapping, measurement, etc.). This asymptotic channel-loss-invariant fidelity is illustrated in Fig. 4d. While increasing the distance between adjacent nodes increases the round-trip time and thus the decoherence in one clock cycle, Fig. 4c shows that the asymptotic infidelity increases less than it would have if it were to depend on the channel loss as well.

Discussion

Though the complete bipartite connectivity of routers may appear challenging to implement, a router can be added to a standard multiplexed repeater with relatively little physical resource overhead. Figure 5 illustrates one such realization using photonic integrated circuits (PICs). Quantum registers are integrated onto PICs that contain an array of Mach–Zehnder interferometers (MZIs)²⁴, forming a fast switching network to connect any register to any output channel. For a standard multiplexed k-way repeater with no local connectivity, this requires an m × k switch to connect m repeaters to any of the possible k neighbors in the network, as shown in Fig. 5a. However, a router can be embedded in this architecture by extending this to an m × (k + 2) switch. The additional two ports lead to a detector station as shown in Fig. 5b, thus enabling photon-mediated entanglement between any two registers in the repeater. Since typical single-photon detectors have dead times of a few tens of nanoseconds, a single pair of detectors could facilitate many attempts at local entanglement in a single repeater clock cycle, which may be hundreds of microseconds long depending on the length of the link being connected. The additional complexity involved in adding these two additional channels is small, making this approach an attractive option for implementing all-to-all local connectivity.

Fig. 5: Potential physical realization of k-way repeater nodes with m repeater qubit registers.

The main component of our proposed router architecture is a photonic switch that provides all-to-all connectivity from ports on one side of the switch to ports on the other side. Photonic switches can take the form of a tree of Mach–Zehnder interferometers (MZIs) when the modes (Fig. 2) are temporally multiplexed or a wavelength-division multiplexer when the modes are spectrally multiplexed. a Standard repeater realization. A standard (routerless) repeater can be constructed using an m × k switch that connects all m repeater registers with the k links that go to other nodes in the network. b Router realization. A router can be constructed using an m × (k + 2) switch. Photons emitted by the m repeater registers can travel to the k links that go to other nodes in the network, or they can be sent to a local detector station for local entanglement generation. c MZI implementation of k = 4-way, m = 8-register router. A k-way, m-register router can be implemented using an MZI array of depth ${\log }_{2}({m}^{2}k/2)$, comprising a register routing layer (depth $2{\log }_{2}(m/2)$), an interposer for routing from local to distant connections (depth 1), a network routing layer (depth ${\log }_{2}(k)$), and a local BSM layer (depth 1). The ends of the MZI array are coupled either directly to detectors for the local BSMs or a frequency conversion stage followed by fiber links to distant detector stations for networking. All losses considered in our simulations are shown here.

On a PIC, the m × k switch required for the routerless repeater can be realized on an MZI array of depth ${\log }_{2}(m)+{\log }_{2}(k)$²⁵. However, this architecture does not permit simultaneous routing from multiple memories, which is desired for the local entanglement operations used in the quantum router. In Fig. 5c, we present an architecture that permits arbitrary m × k routing for connecting registers to the network, allows simultaneous routing from two memories to perform Bell state measurements for local entanglement generation, and maintains ${{{\mathcal{O}}}}(\log m)$ scaling of the array depth. The addition of a one-MZI interposer permits routing between the network and a Bell state measurement setup for local entanglement generation (see Supplementary Note 4 for more details). The simulations presented in Fig. 4 utilize this architecture assuming an aluminum nitride (AlN)-based photonic chip; alternative implementations include using silicon nitride (SiN)²⁶ or lithium niobate (LN)¹⁷. The control requirements for such large MZI arrays are similar to those required by and demonstrated for optical neural nets²⁷ and programmable photonic circuits^28,29, allowing us to take advantage of this existing technology for our router. Additional improvements include integrating detectors on-chip³⁰ to eliminate the off-chip coupling inefficiency for local measurements and integrating the frequency conversion stage on-chip, which is feasible in highly nonlinear materials such as LN³¹.

This platform is an attractive path for realizing recent proposals for on-chip polarization-to-spin based networking³². The PIC implementation presents an additional benefit if the links to Alice and Bob have different transmissivities. Since both the rate and fidelity of entanglement distribution are limited by the difference in the time needed to establish entanglement with both Alice and Bob, the repeater in Fig. 2b (with equal numbers of registers in the Alice and Bob banks) will be limited by the lossier side. In contrast, the PIC implementation allows dynamic allocation of registers to Alice and Bob to balance the rates of entanglement generation. This optimizes the entanglement rate by effectively increasing the multiplexing on lossier ports, and optimizes the entanglement fidelity by preventing a build-up of idling registers on a lower-loss port. Dynamic memory allocation is also of great importance for managing entanglement flows in general 2D quantum network geometries^33,34,35.

The router architecture has additional advantages in multi-repeater quantum networks. The high local connectivity of the router enables chains of repeaters to automatically connect the longest available entanglement links, favoring the generation of a single EPR pair shared between distant nodes over that of multiple EPR pairs shared between relatively proximate nodes. Specifically, the first-in, first-out behavior of a router guarantees that entanglement will always grow from the longest established chain. In contrast, even if we allow adjacent standard repeaters to have all-to-all connectivity between registers in adjacent nodes (e.g., by spectral shifting or time-bin reordering), there is no guarantee that the longest links will be generated first.

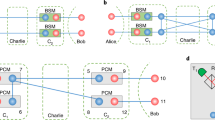
This behavior is illustrated in Fig. 6, which compares the dynamics of a standard network and a router network under similar scenarios. Before each clock cycle, a repeater or router will determine which links to attempt on the subsequent clock cycle given the current link state. An example is shown in Fig. 6a. If we further allow the standard repeater to have knowledge of the global network state, it can adjust its transmission sequence to prioritize a longer link, e.g., by attempting to entangle registers B5 and C6 (instead of B5-C5 and B6-C6). In contrast, the router does not require any information about the network state; each register simply attempts entanglement with a fixed partner in a neighboring node.

Fig. 6: Dynamics of repeater chains.

Four repeater nodes in each chain are shown for both the standard repeater chain (left panels) and the router chain (right panels). Both chains have the same number of successful entanglement links. Registers in each node are labeled from A1 to D6. a State of the chain before the entanglement attempts during some clock cycle t. The entanglement attempts to be made in clock cycle t are shown as dashed lines. b State of the chain after the entanglement attempts during clock cycle t, but before Bell state measurements are performed. Bell state measurements in the router chain are performed according to the first-in-first-out strategy. c Link state after Bell state measurements during clock cycle t. The standard repeater chain has one long link that spans all four nodes, but the router chain has two long links. The standard repeater chain is unable to connect the shorter links that are available to form long links.

Figure 6b shows a possible network state after the entanglement attempts in a clock cycle. Each router uses local entanglement and Bell state measurements to connect its left and right banks of registers. Following a first-in-first-out strategy, it connects the first available entangled register in the left bank with the first available entangled register in the right bank and repeats until only unentangled registers remain in one of the banks. Using only local information, the router network thus automatically connects as many long links as possible, as demonstrated by the link state in Fig. 6c. On the other hand, the standard repeater may not be able to connect long links even if there are enough successful entanglements to do so. As a result, the state of the standard network after this time step yields some long links, but also many singular short links that cannot be merged.

The router’s strategy reduces the idling time between local entanglement generation and the delivery of this entanglement to the end users, thereby increasing the fidelity of the delivered entanglement. We highlight that this router behavior is realized without any need for knowledge of the global network state. In a true deployed network, communication latencies prevent individual nodes from knowing the state of the total network in real-time, making the router’s ability to optimize fidelity with local-only information all the more notable.

In conclusion, we have addressed a critical problem in quantum repeater architectures: minimizing memory latencies to maintain entanglement fidelity across repeater networks. Specifically, the quantum router architecture enables entanglement fidelity that is invariant to the channel losses in the network. Our architecture applies to leading entanglement protocols and automatically prioritizes entanglement flows using only local information. An important next step will be to exploit the local connectivity for entanglement distillation³⁶ and local error correction³⁷ to further improve the fidelity of generated entanglement. In this way, the entanglement rate can be traded for entanglement fidelity, without modification to the router architecture. While the above analysis considered NV centers in diamond, the architectural benefits should apply to other quantum memory modalities, including solid-state artificial atoms, trapped ions, and neutral atoms. In suitable parameter regimes, routers can also incorporate multiplexing into realizations of distance-independent entanglement rates using local GHZ projective measurements³⁸. Our results emphasize the importance of local connectivity in designing multiplexed quantum repeaters for high-rate and high-fidelity entanglement distribution across quantum networks.