Introduction

Quantum decoherence, resulting from the unavoidable coupling between a qubit and its environment, underlies fundamental descriptions of the quantum-classical transition1,2 and poses a major challenge to a variety of quantum technologies3. Several methods exist to mitigate environment-induced decoherence. Materials-based approaches aim to perfect the environment through techniques like surface passivation and optimized synthesis4,5,6,7. Dynamical decoupling instead relies on manipulating the qubit rapidly enough to average out deleterious environmental fluctuations at particular frequencies8,9,10,11. However, the flexibility and power of this technique comes at some cost to the qubit’s utility, as the decoupling pulses need to be interleaved with gate operations or sensing sequences12. An alternative and complementary approach aims at manipulating the noise frequency spectrum of the bath itself, a technique referred to as spin-bath driving13 and originally developed in nuclear magnetic resonance and known as spin decoupling14. Recent work has shown that monochromatic driving of a spin bath can extend the coherence of bulk15 and near-surface NV centers16,17. An intrinsic limitation of this monochromatic approach is that it does not efficiently address spectrally broad classes of spins that naturally emerge in inhomogeneous environments and interacting spin baths18.

In this work, we apply a polychromatic drive scheme to a single qubit system and demonstrate experimentally that spectrally engineered driving of a spin bath enhances qubit coherence beyond the limit of what can be achieved with monochromatic driving. The drive is an extension of broad-band decoupling methods18,19,20,21,22 used in nuclear magnetic resonance and operates in analogy to motional narrowing: driving the spin bath accelerates incoherent bath fluctuations, reducing the integrated phase acquired from the spin bath. Our driving scheme not only enables significantly increased power efficiency for protecting coherence, it also paves the way toward more complex and powerful techniques of tailored dynamical bath engineering.

Figure 1a shows a model of the system we investigate. The polychromatic drive is applied to the spin environment of a shallow nitrogen-vacancy (NV) center in diamond (see Methods for details on the diamond sample preparation). The NV center is a solid-state qubit that exhibits long coherence in ambient conditions and is being used in a variety of applications ranging from networking to quantum sensing. This work uses NV centers located just a few nanometers below the diamond surface, where they are exposed to magnetic noise originating from surface electronic spins23,24,25,26,27. The surface character of the spin bath is documented for example in16,23,26,28 where the coupling to g = 2 spins is measured as a function of NV depth, found to be sensitive to surface treatment, and also corroborated by the lack of a g = 2 signature for bulk NVs.

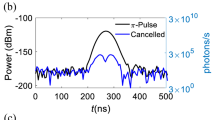
Fig. 1: Coherence extension by driving the spin bath.
figure 1

a A shallow NV center (qubit) is dephased by the magnetic noise originating from a bath of surface spins. b Hahn-echo sequence used to measure coherence during bath driving with linewidth Δν and Rabi frequency Ωss. c Coherence decay without driving (gray), with monochromatic driving (blue) and polychromatic/stochastic driving (orange), described in the text. Solid lines are fits to \(\exp \left[-{(\tau /{T}_{2})}^{n}\right]\). Error bars correspond to ± one standard error of the mean.

Full size image

Radio-frequency (rf) fields, delivered by a single free-space antenna, enable coherent control of NV qubit states \(\{\left|{m}_{s}=0\right\rangle ,\left|{m}_{s}=-1\right\rangle \}\) and surface spin qubit states \(\{\left|\uparrow \right\rangle ,\left|\downarrow \right\rangle \}\). NV centers are addressed individually by means of a home-built confocal microscope operating in ambient conditions, and are subjected to a static magnetic field B0 ≈ 315 G aligned along the NV axis. We use green (532 nm wavelength) laser pulses for initialization and readout of the NV spin state. The NV coherence C(τ) is probed using the Hahn-echo sequence represented in Fig. 1b; simultaneously, the surface spins are driven with spectrally engineered rf fields. Specifically, we apply drives with Lorentzian spectral line shapes characterized by a tunable full-width at half maximum (FWHM) Δν, generated by stochastic phase modulation of a carrier wave with Rabi frequency Ωss on the surface spin transition, denoted as a stochastic drive (see Methods for details). Spectrum engineering via phase modulation (as opposed to amplitude modulation) is a key feature of the experiment, ensuring that the driving power remains constant, whereas amplitude modulation could cause fluctuating AC Zeeman shifts of the NV spin states and decohere the NV16. The NV coherence time T2 is extracted from a stretched exponential fit (\(\exp \left[-{\left(\tau /{T}_{2}\right)}^{n}\right]\)) to the measured coherence decay shown in Fig. 1c.

Results

Bath driving

To understand the effect of bath driving on the qubit’s coherence, we first give a quantitative description of NV decoherence based on a model of the surrounding bath. The NV coherence C(τ) is determined by the overlap between a filter function and the noise spectral density29,30,31,32:

$$C(\tau )=\exp \left[-\frac{1}{\pi }\int\nolimits_{0}^{\infty }d\omega S(\omega )F(\tau ,\omega )\right],$$
(1)

where

$$S(\omega )={\gamma }^{2}\int\nolimits_{-\infty }^{\infty }{e}^{-i\omega t}\langle B(t^{\prime} +t)B(t^{\prime} )\rangle dt,$$
(2)

is the magnetic noise spectral density experienced by the NV (see Fig. 2c, d), γ is the gyromagnetic ratio, B is the field component along the NV axis, \(F(\tau ,\omega )=8/{\omega }^{2}{\sin }^{4}(\omega \tau /4)\) is the qubit Hahn-echo filter function, and ω is the angular frequency. This decoherence model assumes a random Gaussian distribution for the noise amplitudes and is valid in the regime of pure dephasing.

Fig. 2: Principle of monochromatic and stochastic bath driving.
figure 2

Time-domain representations of the magnetic noise B(t) produced by a spin bath, (a) for monochromatic driving (blue) and (b) for stochastic driving (orange). For simplicity, all the spins are assumed to have the same resonance frequency. Frequency domain representations of the noise spectral density S(ω), (c) for monochromatic driving (blue) and (d) for stochastic driving (orange). Both driving methods reduce the overlap between the filter function F(τ, ω) (dashed line) and the noise spectrum, as compared to the undriven case (gray curve), resulting in increased coherence.

Full size image

Our strategy to decouple the qubit from its noise environment relies on actively reshaping the spectral density so that it minimally overlaps with the filter function. This decoupling mechanism and its underlying microscopic model are illustrated in Fig. 2. The upper panels are time-domain representations of the magnetic noise B(t) produced by the surface spins, and the lower panels are the corresponding frequency domain representations S(ω). We now illustrate three cases of driving: no driving, monochromatic, and stochastic.

In the absence of driving (gray curve in Fig. 2), intrinsic spin relaxations at a rate Γ lead to a random process for the noise, characterized by a correlation time τc = 1/Γ in the time domain (Fig. 2a, b) and a Lorentzian spectrum with half width at half maximum (HWHM) Γ centered at ω = 0 (Fig. 2c, d). The overlap of the noise spectrum with the Hahn-echo filter function sets the contribution of surface spins to NV decoherence.

In the case of resonant monochromatic bath driving with a Rabi frequency Ωss, the surface spins undergo Rabi flopping in addition to their intrinsic relaxation dynamics, leading to oscillations of the field B(t) in the time domain (blue curve in Fig. 2a). In the frequency domain (Fig. 2c), monochromatic driving shifts the center of the spectral density from 0 to Ωss; the overlap with the qubit filter function (represented by the blue shaded area) is consequently reduced from the undriven case.

In contrast, stochastic driving consists of a continuum of frequency tones with random phase relations. Each tone drives partial Rabi oscillations of the surface spins and the incoherent sum of these Rabi oscillations results in random evolution as shown in Fig. 2b). These incoherent dynamics lead to an effective relaxation rate R induced by stochastic driving, on top of the intrinsic relaxation rate Γ (see Supplementary Note 3). In the case of a broad Lorentzian driving spectrum Δν ≫ Ωss, Γ,

$$R={{\Gamma }}+2\frac{{{{\Omega }}}_{\,{{\mbox{ss}}}\,}^{2}}{{{\Delta }}\nu }.$$
(3)

In the frequency domain (Fig. 2d), the effect of the stochastic drive is to broaden and flatten the noise spectral density. The overlap with the filter function is reduced, leading to an extension of coherence.

In summary, both monochromatic and stochastic driving decouple surface spins by inducing magnetic fluctuations that are fast compared to the Hahn-echo phase sensing time. Compared to monochromatic driving, the advantage of stochastic driving is that it more efficiently addresses the broad spectral range of spins observed in real settings.

Probing bath dynamics under drive

Having discussed the predicted spin dynamics under stochastic excitation and its potential for extending qubit coherence, we now experimentally characterize the frequency and time response of the surface-spin bath and the effects of stochastic driving. We use the NV to probe the surface spins dynamics with the double electron-electron resonance (DEER) sequence shown in Fig. 3a. The Hahn-echo sequence on the NV cancels out low frequency noise from the environment, but the DEER pulse (duration tss, center frequency fss and spectral width Δν) selectively recouples the surface spins and reveals their dynamics.

Fig. 3: Probing bath correlations to quantify noise spectrum under drive.
figure 3

a Pulse sequence used to probe the surface spin bath, and (b) corresponding spectrum with Δν = 0, tss = 60 ns, τ = 20 μs, Ωss/2π = 9.7 MHz, and an NV π-pulse of 80 ns. c Experimental spin bath dynamics, obtained by measuring NV coherence as a function of pulse length tss for different excitation line-widths Δν and for Ωss/2π = 8.7 MHz. Increasing Δν accelerates the damping of the Rabi oscillations, eventually reaching an overdamped regime. d Noise spectral densities obtained by Fourier transformation of the fitted DEER signals in (c) and normalized so that \(2\int\nolimits_{0}^{\infty }S(\omega )d\omega /2\pi =1\). Gray shaded area represents the Hahn-echo filter function corresponding to a sequence duration of τ = 10 μs. Error bars represent ± one standard error.

Full size image

Figure 3b shows the NV coherence as a function of fss, where the fixed pulse duration tss = 60 ns is chosen to be a π-pulse on resonance with the surface spins. The acquired spectrum exhibits a resonance at (885.3 ± 0.4) MHz which is the magnetic signature of a g = 2 spin-1/2 particle in the applied static field of 315 G. The line-shape is best modeled by assuming inhomogeneous broadening of the surface spins and accounting for the finite pulse width tss (see Supplementary Note 3 for details). From the fit, we extract the FWHM of the underlying Gaussian distribution of the spins 2Γ2 = (15.7 ± 1.3) MHz.

Having confirmed the electronic nature of the surface spins and identified their inhomogeneous broadening, we now investigate the temporal response of the bath. Figure 3c shows the measured NV coherence as a function of tss for different line-widths Δν of the drive and a fix sequence duration τ = 16 μs. When Δν = 0, the NV coherence exhibits damped oscillations as a function of tss. The oscillations reflect the Rabi flopping of the surface spins while the damping is due to the inhomogeneous broadening and the intrinsic relaxation. For Δν > 0, the stochastic DEER pulse decorrelates the field produced by the surface spins between the first and second half of DEER sequence, leading to increased damping of the Rabi oscillations. For Δν/2π = 48 MHz > 2Γ2, the measured NV coherence decays exponentially at a rate given by Eq. (2), as expected for broad Lorentzian excitation. The solid curves in Fig. 3c are fits using our model of inhomogeneously broadened surface spins subjected to a stochastic drive (see Supplementary Note 3). From these fits, we extract an independent measure of the inhomogeneous broadening 2Γ2 = (14.9 ± 1.2) MHz in agreement with the DEER spectrum in Fig. 3b, and a Rabi frequency Ωss/2π = (8.7 ± 0.1) MHz.

To investigate the noise spectrum generated by the measured surface spin dynamics, Fig. 3d shows the Fourier transform of the fitted bath correlations of Fig. 3c obtained after symmetrization with respect to tss = 0. We constrain the integrated power of the spectra to be constant. As expected from the time domain dynamics, the spectrum under monochromatic driving (Δν = 0) exhibits a peak at Ωss/2π, but still has a remaining static component due to the detuned Rabi oscillations of the inhomogeneously broadened spins (the simplified Fig. 2 schematic does not account for this inhomogeneous broadening). In the case of stochastic driving, the noise spectrum is flattened and broadened, and the overlap with F(τ, ω) is considerably reduced.

T 2 extension

We now demonstrate that stochastic driving extends NV coherence beyond the gains of monochromatic bath driving. We perform the sequence shown in Fig. 1b and measure the NV coherence time \({T}_{2}\left({{{\Omega }}}_{{{\mbox{ss}}}},{{\Delta }}\nu \right)\). We observe that stochastic driving outperforms monochromatic driving over a broad range of drive parameters. Figure 4 shows the coherence time T2(Ωss, Δν), where the bare coherence time T2(Ωss = 0) = (33.1 ± 1.5) μs. Figure 4a, b highlight the Δν and Ωss dependences, respectively. For example, we measure a 2.7-fold increase in coherence time with stochastic driving at (Ωss/2π = 4.9 MHz, Δν/2π = 17.4 MHz), as compared to a 1.8-fold increase with monochromatic driving at the same power. Our experimental data are well-captured by Eq. (1) where S(ω) includes contributions from two g = 2 spin baths (both are driven, but have different bath parameters), and a residual bath that is undriven (see Supplementary Note 3 for details). Details of how the extracted stretch exponent n varies with bath driving parameters are given in Supplementary Note 6.

Fig. 4: Coherence time for different driving parameters.
figure 4

a NV T2 as a function of Δν for different bath Rabi frequencies Ωss. Stochastic drive outperforms monochromatic drive (Δν = 0). For very weak driving fields (Ωss/2π = 0.0 MHz), the stochastic phase modulation is ineffective and T2 is independent of Δν. b T2 as a function of drive Rabi frequency Ωss for monochromatic driving Δν = 0 and stochastic driving with Δν/2π = 17 MHz. Solid lines are fit using our model (see Supplementary Note 3 for details). Error bars correspond to ± one standard deviation of the T2 estimate.

Full size image

Our results suggest that, for a given driving power, an optimal Δν exists that maximizes the coherence. The non-monotonic dependence on Δν can be understood intuitively as follows: starting from Δν = 0, increasing Δν enables a larger fraction of the inhomogeneously broadened surface spins to be resonantly addressed and therefore decoupled from the NV center. When Δν exceeds the inhomogeneous broadening of the surface spins (reported above as 2Γ2 ~ 16 MHz), drive energy is spread over non-resonant frequencies and the power efficiency of stochastic driving decreases.

Figure 4b also shows that stochastic driving reduces coherence at the lowest Rabi frequencies, an effect also captured by our model. Intuitively, as Ωss first increases from zero, the noise spectral density broadens, increasing in overlap with the filter function (see Fig. 2d) and decreasing the coherence, before broadening well beyond the peak and flattening out. In Supplementary Note 4, we derive the condition for stochastic driving to increase coherence: \(\sqrt{{{\Gamma }}R}\gtrsim 2\pi /{T}_{2}\). Incorporating two driven baths with long- and short-lived correlations (as suggested by33) in our model is essential to quantitatively capture the features of Fig. 4a, b, including the drop of coherence discussed above as detailed in Supplementary Note 4. From the fit in Fig. 4b, we extract the correlation times of the two driven baths: (68 ± 17) μs and (0.37 ± 0.05) μs.

Finally, we provide a qualitative explanation for the gains of stochastic driving relative to monochromatic driving. In order to completely decouple an ensemble of inhomogeneously broadened spins, monochromatic driving relies on power broadening and requires Ωss ≫ Γ2. On the other hand, stochastic driving naturally addresses all the spins as long as Δν ≳ Γ2. Combining this relation with Eq. (2), the condition for decoupling all the spins in the case of stochastic driving is \({{{\Omega }}}_{{{\mathrm{ss}}}}\gg \sqrt{{{\Gamma }}{{{\Gamma }}}_{2}}\). Therefore, stochastic driving outperforms monochromatic driving as long as Γ < Γ2, which is often satisfied and, for example, is satisfied by several orders of magnitude for near-surface NV qubits. For the surface spin bath investigated here, we observe Γ2 ~ 10 MHz, and expect Γ ~ 0.03 MHz as reported in34 (consistent with our observations), explaining the better performance of stochastic driving as Γ ≪ Γ2.

Discussion

A practical advantage of stochastic driving is that it reduces the driving power required to achieve a given coherence extension. AC Zeeman shifts of the qubit energy levels and heating at high rf driving powers are experimental limitations to the coherence time that scale with drive power ( ∝ ∣Ωss∣2)16. For example, Fig. 4b shows that doubling the coherence necessitates Ωss/2π ≈ 3 MHz for stochastic driving, and ≈8 MHz for monochromatic driving, corresponding to a 7-fold power reduction when stochastic driving is used. This advantage may prove crucial for avoiding heating and other undesired effects, in particular for cryogenic systems like superconducting qubits35, which could also benefit from spin bath driving techniques. While coherent driving of surface electric dipoles that decohere trapped ion qubits36,37,38,39 or NV qubits40 may be infeasible, this work suggests that such dipoles could possibly be incoherently driven and motionally narrowed.

In this work, we have considered only driving with a Lorentzian spectrum, but other types of polychromatic driving could be even more advantageous. The drive could for example be engineered to precisely cover the exact spectral shape of the noise sources, and engineering alternative spectral shapes could also enable maximization of the coherence at a desired Rabi frequency. As a proof of concept, we show in Supplementary Note 5 that a Gaussian spectrum for the drive performs better than a Lorentzian spectrum at specific Rabi frequencies. A more complex but potentially also more powerful approach would be to not use any pre-existing knowledge of the noise spectrum, but instead, apply real-time reinforcement learning to converge toward a drive waveform that maximizes the coherence time T2 of the NV. Ultimately, complex polychromatic waveforms could be used to exploit correlations among bath spins.

In conclusion, we demonstrate the extension of coherence of a qubit by driving its spin environment with spectrally engineered fields. We show that stochastic driving of the surface-spin bath of shallow NV centers is more efficient than monochromatic driving, and corroborate our findings with a quantitative model. Further improvements, especially for mesoscopic baths, may be possible using customized structured drive waveforms. Beyond extending coherence, spectrally engineered driving of the spin environment has much broader applications than merely extending coherence. As an example, recent work has used stochastic driving of an NV center’s spin bath to probe the many body dynamics of the bath41.

Methods

Diamond sample fabrication

The diamond substrate consists of a commercial Element Six electronic grade (100) diamond plate with dimensions 2 mm × 2mm × 0.15 mm on top of which a 50 nm-thick layer of isotopically purified diamond (99.999%12C methane precursor gas) is grown by plasma-enhanced chemical vapor deposition. Shallow NV centers are formed by nitrogen-14 implantation (dose = 5.2 × 1010 cm−2, tilt = 7∘, energy = 4 keV) followed by high-temperature annealing. The target NV depth is 7 nm. The diamond surface was patterned and etched with O2 plasma to form nanopillars with diameter 400 nm and height 500 nm, enabling enhanced collection efficiency.

Stochastic drive

For driving surface spins, we use phase modulated rf fields with Lorentzian line shapes centered on the surface spin transition frequency. The modulation scheme is chosen to minimize fluctuations of NV energy levels caused by varying AC Zeeman shifts16, which would introduce additional dephasing. A driving field with Rabi frequency Ω and detuning Δ−1 ≫ Ω from the \(\left|{m}_{s}=0\right\rangle \to \left|{m}_{s}=-1\right\rangle\) NV transition frequency causes an AC Zeeman shift equal to Ω2/2Δ−1. While amplitude modulation causes variations of AC Zeeman shift on the order of Ω2/Δ−1, phase modulation introduces variations smaller by a factor Δν/Δ−1 ~ 0.01.

Following the phase-diffusion model for lasers42, we describe the driving field as \(\exp \left[-i(\nu t-\phi (t))\right]\), where the phase ϕ(t) is a stochastic process chosen to produce the desired spectrum. The desired Lorentzian spectrum implies that the wave auto-correlation function has the form of an exponential decay:

$$\left\langle {e}^{-i\phi (t)}{e}^{i\phi (t^{\prime} )}\right\rangle ={e}^{-\frac{{{\Delta }}\nu }{2}| t-t^{\prime} | }.$$
(4)

One choice of ϕ(t) that satisfies relation (4) is a Gaussian random walk43, which we use here for generating our stochastic waveforms. The standard deviation σ for the normally distributed steps should follow:

$$\sigma =\sqrt{{{\Delta }}\nu \,\delta t},$$
(5)

where δt is the sampling time of the phase trace ϕ(t).

Once the random walk ϕ(t) is computer generated, the I and Q modulation parameters are given by the real part and imaginary part of \(\exp [i\phi (t)]\) respectively.

We use an arbitrary waveform generator (Keysight M8190A) to output the IQ signals and perform phase modulation of a microwave source (Stanford Research Systems, Inc, SG384). For this work, we used a time window of 100 μs and 200,000 samples corresponding to a sampling rate of 1/δt = 2 GHz for the IQ signals. We control the shape and calibrate the bandwidth of the generated rf drives using a spectrum analyzer.