Introduction

The most serious obstacle towards fault-tolerant quantum computation is probably quantum error correction. The reason is that quantum error correction requires a large Hilbert space as well as high-fidelity measurement and control. The use of a harmonic oscillator, i.e., a bosonic system, is one strategy to obtain a large Hilbert space without too much hardware overhead1,2,3,4. In this system, information can be encoded as a symmetric pattern in phase space. Such a symmetry can be either translational (Gottesman–Kitaev–Preskill code)5,6 or rotational (cat or binomial code)7. In a superconducting circuit8,9,10,11,12, which is our working system, another advantage of using a harmonic oscillator is that the major loss mechanism is single-photon loss; thus, quantum error correction in this system can be achieved by detecting the number parity of the photon state13,14,15.

Recently, autonomous quantum error correction (AQEC) schemes have gained considerable attention to avoid complicated measurements and feedback16,17,18,19,20,21,22,23,24,25. Although AQEC is considered to be much easier to implement than the conventional measurement-based quantum error correction, there is still a serious hardware overhead—the need for many microwave tones. The origin of this problem is that the logical qubit states are composed of multiple Fock states, and errors are corrected by selective transitions induced by continuous microwave tones. Since each transition requires a separate continuous microwave tone, many microwave tones are required to handle all possible transitions. For example, eight microwave tones are used in ref. 24 although the logical qubit states in this reference are composed of only four Fock states. Moreover, the amplitude of each tone must be tuned independently to ensure identical transition rates that prevent leakage of which-path information. Thus, any scheme based on state-by-state correction in the Fock basis is difficult to scale up.

In this study, we propose an AQEC scheme that requires only a single continuous microwave tone—the simplest possible error correction scheme that can surpass the break-even point. This substantial reduction of hardware overhead is due to the protection of the Hilbert space for encoding and error correction such that the system remains in this protected Hilbert space under single-photon loss/drive. Such a protection is provided by a four-photon pump applied to a Kerr nonlinear oscillator—a system with a small anharmonicity of <1% of its resonance frequency26. Since this four-photon pump cannot be achieved by simple linear driving and must be achieved by parametric modulation of the Josephson junction energy27,28 (see Supplementary Note 1), we term this system a four-photon Kerr parametric oscillator (KPO). Although a KPO has received much attention very recently because of its use for the generation and stabilization of the cat states29,30,31,32,33,34,35,36,37,38, gate-based quantum computation30,34,38,39,40,41,42, measurement-based error correction43,44, quantum annealing45,46,47,48,49,50,51, and other physically interesting topics52,53,54,55,56,57,58,59, little attention has been paid to its applicability to AQEC. Our study reveals that a KPO can be a suitable system for AQEC.

Results

System and encoding

Our system of interest is a KPO driven by a four-photon pump whose frequency is ωp. In the rotating frame with the frequency ωp/4, the Hamiltonian of the KPO is given by (see the section “Gate operation and circuit implementation” and Supplementary Note 1 for circuit implementation and derivation of the Hamiltonian)

$$\begin{array}{ll}{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{KPO}}}}}=\hslash {{{\Delta }}}_{{{{\rm{KPO}}}}}{\hat{a}}^{{\dagger} }\hat{a}-\hslash \dfrac{K}{2}{\hat{a}}^{{\dagger} }{\hat{a}}^{{\dagger} }\hat{a}\hat{a}+\hslash \dfrac{P}{2}({\hat{a}}^{{\dagger} }{\hat{a}}^{{\dagger} }{\hat{a}}^{{\dagger} }{\hat{a}}^{{\dagger} }+\hat{a}\hat{a}\hat{a}\hat{a}).\end{array}$$
(1)

Here, \(\hat{a}\) and \({\hat{a}}^{{\dagger} }\) are the ladder operators for the KPO, ΔKPO(≡ωKPO−ωp/4) is the KPO-pump frequency detuning, where ωKPO is the transition frequency of the KPO between \(\left|0\right\rangle\) and \(\left|1\right\rangle\) states, K is the Kerr coefficient, and P is the amplitude of the pump.

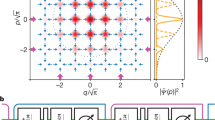
The four highest quasienergy states from Eq. (1) are energetically close and show fourfold rotational symmetry in phase space as shown in Fig. 1a. These states are represented by the modulus of 4 in the Fock basis:

$$\begin{array}{r}\left|{k}_{{{{\rm{mod}}}}}\right\rangle =\mathop{\sum }\limits_{n=0}^{\infty }{C}_{n}^{(k)}\left|4n+k\right\rangle ,\end{array}$$
(2)

where \(\left|\right.{C}_{n}^{(k)}{\left|\right.}^{2}\) (k ∈ {0, 1, 2, 3}) indicates the occupation probability of each Fock basis, which is plotted in the upper panel of Fig. 1a.

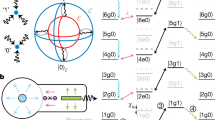
Fig. 1: Information encoding and AQEC scheme in a four-photon KPO.
figure 1

a Four eigenstates in the information space. The upper panel shows the occupation probability of these eigenstates in the Fock basis at ΔKPO/K = 1.5 and P/K = 0.2764 (indicated by a vertical dashed line in the inset), where the energy levels of \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) (\(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\)) are degenerate. Here, E0 is the energy level of \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\). The inset shows the quasi-energy levels of the four eigenstates as a function of P. The four lower panels show the Wigner distribution of the four eigenstates. The eigenstates with the odd/even number parity consist of the code/error space. b Requirements for AQEC. The dash-dot line forming the gray boundary represents protection of the information space provided by the four-photon pump. Double arrows (⇒) indicate induced transitions, and single arrows (→) indicate spontaneous transitions caused by single-photon loss. Colors of bars and frames in this figure indicate the modulus of 4 in the Fock basis.

Full size image

We encode information on the states with the odd number parity24—\(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) as \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\) as \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\), where the subscript L denotes the logical qubit states. These two logical states comprise the code space (warm colors in Fig. 1), whereas the remaining two states with even number parity constitute the error space (achromatic colors). In this work, we call the code space and error space together the information space (the gray dash-dot boundary in Fig. 1b).

Note that there is an energy gap, which we call the protection energy gap, the size of which is about 3K at ΔKPO and P values shown in the caption of Fig. 1a. This energy gap protects the information space by suppressing the population leakage to states outside of the information space, which we name ‘higher excitation levels (HEL)’ although their quasienergies are actually lower because of the minus sign in front of K [Eq. (1)]. (The quasienergy level diagram showing the protection energy gap and the HEL space are shown in Supplementary Fig. 4).

We can access \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\) by increasing P in Eq. (1) adiabatically from \(\left|1\right\rangle\) and \(\left|3\right\rangle\), respectively32,34. In the section “Unconditional reset”, we discuss another convenient way to reset the state of the system to the logical qubit states unconditionally by applying two continuous microwave tones.

Error correction scheme

Our autonomous error correction scheme is shown in Fig. 1b. Our scheme corrects errors caused by single-photon loss and thus relies on change in the number parity of the KPO state18. The crucial observation is that if \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) (\(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\)) loses one photon, the final state is likely \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) (\(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\)) because of the protection by the four-photon pump. This means that we can recover \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) from \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) (\(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\) from \(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\)) by applying a single-photon drive. Note that we cannot ask which Fock state loses or gains the photon as all Fock states comprising the logical qubit state change simultaneously. This eliminates the need to control the Fock states one by one, thus greatly reducing hardware overhead.

The second essential requirement, other than the protection of the information space, is the energy degeneracy between \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) as well as between \(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\). Remarkably, this can be achieved simply by tuning P in Eq. (1) to the value indicated by the vertical dashed line in the inset of Fig. 1a. The energy degeneracy allows us to induce transitions between \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) as well as between \(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\) using a single microwave tone with the frequency ωp/4.

Other requirements for our AQEC scheme are (i) one-way transition: \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle \to \left|{1}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{2}_{{{{\rm{mod}}}}}\right\rangle \to \left|{3}_{{{{\rm{mod}}}}}\right\rangle\), and (ii) no transition: \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\,\nleftrightarrow \,\left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\, \nleftrightarrow \,\left|{0}_{{{{\rm{mod}}}}}\right\rangle\). The one-way transition can be realized by introducing an ancilla resonator whose ladder operators are \({\hat{b}}^{{\dagger} }\) and \(\hat{b}\), and applying \({\hat{a}}^{{\dagger} }{\hat{b}}^{{\dagger} }+\hat{a}\hat{b}\) instead of \({\hat{a}}^{{\dagger} }+\hat{a}\). (Hereafter, we refer to the microwave tone for \({\hat{a}}^{{\dagger} }{\hat{b}}^{{\dagger} }+\hat{a}\hat{b}\) as the correction tone.) This ancilla resonator must be very lossy compared with the KPO to suppress transitions from the code space to the error space. The resulting process is as follows. For example, \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) can be corrected with the ancilla, whose state is written with the subscript ‘an’, as

$$\left|{0}_{{{{\rm{mod}}}}},{0}_{{{{\rm{an}}}}}\right\rangle \Rightarrow \left|{1}_{{{{\rm{mod}}}}},{1}_{{{{\rm{an}}}}}\right\rangle \to \left|{1}_{{{{\rm{mod}}}}},{0}_{{{{\rm{an}}}}}\right\rangle ,$$
(3)

where ⇒ indicates a transition induced by the correction tone, whereas → indicates a spontaneous transition in the lossy ancilla. Transitions such as \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle \leftrightarrow \left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle \leftrightarrow \left|{0}_{{{{\rm{mod}}}}}\right\rangle\) can be suppressed by an energy gap ωgap (different from the protection energy gap). Note that we have this energy gap already—see the inset of Fig. 1a.

Numerical simulation

We simulate our AQEC scheme by solving the following master equation43 with QuTiP60,61.

$$\begin{array}{l}\dfrac{\partial \rho (t)}{\partial t}=-\dfrac{{{{\rm{i}}}}}{\hslash }[{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{full}}}}}(t),\rho (t)]\\ \qquad\qquad+\left\{{\gamma }_{{{{\rm{KPO}}}}}(1+{n}_{{{{\rm{th}}}}}){{{\mathcal{D}}}}[\hat{a}]+{\gamma }_{{{{\rm{KPO}}}}}{n}_{{{{\rm{th}}}}}{{{\mathcal{D}}}}[{\hat{a}}^{{\dagger} }]\right.\\ \left.\qquad\qquad+{\gamma }_{\phi }{{{\mathcal{D}}}}[{\hat{a}}^{{\dagger} }\hat{a}]+{\gamma }_{{{{\rm{an}}}}}{{{\mathcal{D}}}}[\hat{b}]\right\}\rho (t),\end{array}$$
(4)

where \({{{\mathcal{D}}}}[\hat{O}]\rho =\hat{O}\rho {\hat{O}}^{{\dagger} }-\frac{1}{2}{\hat{O}}^{{\dagger} }\hat{O}\rho -\frac{1}{2}\rho {\hat{O}}^{{\dagger} }\hat{O}\), γKPO is the single-photon loss rate of the KPO, nth is the number of thermal photons in the KPO, γϕ is the dephasing rate of the KPO, and γan is the single-photon loss rate of the ancilla resonator. In this subsection, we consider only single-photon losses in the KPO and the ancilla resonator. (The effects of nth and γϕ will be discussed in the section “Photon gain and dephasing”) The time-dependent Hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{full}}}}}(t)\) is given by

$$\begin{array}{ll}{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{full}}}}}(t)\approx {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{KPO}}}}}+\hslash {{{\Delta }}}_{{{{\rm{an}}}}}{\hat{b}}^{{\dagger} }\hat{b}+\hslash g({\hat{a}}^{{\dagger} }\hat{b}+\hat{a}{\hat{b}}^{{\dagger} })\\ \qquad\qquad+\hslash {A}_{{{{\rm{cor}}}}}\cos ({\omega }_{{{{\rm{cor}}}}}t)({\hat{a}}^{{\dagger} }{\hat{b}}^{{\dagger} }+\hat{a}\hat{b}).\end{array}$$
(5)

Here, Δan(≡ωan−ωp/4) is the ancilla-pump frequency detuning, where ωan is the resonance frequency of the ancilla resonator, g is the coupling constant between the KPO and the ancilla, and Acor and ωcor are the amplitude and the frequency of the AQEC term, respectively.

The first thing that must be done for AQEC is to find the appropriate ωcor. The result of such a frequency sweep is shown in Fig. 2a. We found a peak in the population of the logical qubit states for ωcor near Δan—a signature of AQEC. This result is consistent with the \({\hat{a}}^{{\dagger} }{\hat{b}}^{{\dagger} }+\hat{a}\hat{b}\) term because Δan corresponds to ωan + ωp/4 in the lab frame. In addition, we found a dip separated from the peak with ±ωgap whose sign depends on the logical qubit state of interest. This dip activates the transitions suppressed by ωgap. Such a peak-dip structure can be understood with the diagram shown in the upper panel of Fig. 2b. In this diagram, our AQEC scheme can be understood as population transfer along the thick gray arrows.

Fig. 2: Autonomous error correction.
figure 2

a Population of the logical qubit states as a function of ωcor after 10 μs of evolution with various Acor. The distance between the peak and the dip is ωgap, which is found to be 12.2 MHz. b Lower panel: Bit-flip process of the logical qubit states with and without AQEC. The upper (lower) envelop of the shaded area is the population of the initial logical state (the orthogonal logical state). The red solid and brown dashed lines indicate the population difference between the upper and lower envelops with and without AQEC, respectively. The number near each curve indicates the corresponding bit-flip time extracted from exponential fitting. The black dash-dot line indicates the longitudinal relaxation in the \(\left|0\right\rangle\) and \(\left|1\right\rangle\) encoding. Upper panel: Frequencies of the microwave tone (not the energy levels) at which transitions are induced among the four eigenstates. The thick gray arrows constitute a graphical summary of our AQEC scheme. c Lower panel: Phase-flip process of the logical qubit states with and without AQEC. The number near each curve indicates the corresponding phase-flip time. The black dash-dot line indicates the transverse relaxation in the \(\left|0\right\rangle\) and \(\left|1\right\rangle\) encoding. Other initial states, \(\left|{-}_{{{{\rm{L}}}}}\right\rangle\), \(\left|{{{\rm{i}}}}{+}_{{{{\rm{L}}}}}\right\rangle\), and \(\left|{{{\rm{i}}}}{-}_{{{{\rm{L}}}}}\right\rangle\), where \(\left|{\pm }_{{{{\rm{L}}}}}\right\rangle \equiv (\left|{0}_{{{{\rm{L}}}}}\right\rangle \pm \left|{1}_{{{{\rm{L}}}}}\right\rangle )/\sqrt{2}\) and \(\left|{{{\rm{i}}}}{\pm }_{{{{\rm{L}}}}}\right\rangle \equiv (\left|{0}_{{{{\rm{L}}}}}\right\rangle \pm {{{\rm{i}}}}\left|{1}_{{{{\rm{L}}}}}\right\rangle )/\sqrt{2}\), present identical results. Upper panel: Population leakage to the error and HEL spaces during the evolution from \(\left|{+}_{{{{\rm{L}}}}}\right\rangle\). The solid and dashed lines represent the populations with and without AQEC, respectively. Other initial states, \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\), yield similar results. The parameters are as follows. KPO: ωKPO/2π = 2.98 GHz, K/2π = 20 MHz, 1/γKPO = 50 μs86. Pump: ΔKPO/2π = 30 MHz, P/2π = 5.5405 MHz. Ancilla resonator: ωan/2π = 4 GHz γan/2π = 0.557 MHz (found in Fig. 3c), g/2π = 7 MHz. Correction tone: ωcor/2π = Δan/2π + 0.36 MHz (found in Fig. 3b), and Acor/2π = 0.25 MHz (found in Fig. 3c).

Full size image

Our main results, the relaxation times with and without AQEC, are presented in Fig. 2b and c. With optimal Acor and γan values (the optimization procedure for these quantities will be discussed in the section “Optimization”), the bit-flip time of the logical qubit states is increased by approximately one order of magnitude (the lower panel of Fig. 2b), and the phase-flip time is increased by over a factor of 6 (the lower panel of Fig. 2c). Note that the phase-flip time is not greater than T2 in \(\left|0\right\rangle\) and \(\left|1\right\rangle\) encoding. This limited performance of AQEC is likely due to different mean photon number between two logical qubit states (see the section “Optimization” for further discussion). The resulting relaxation time of the process fidelity14 surpasses the break-even point by ~20%. We believe that surpassing break-even point will not be too difficult in experiments. The reason is that dephasing due to the low-frequency noise9 was not considered in our simulation—that is T2 = 2T1 in \(\left|0\right\rangle\) and \(\left|1\right\rangle\) encoding, where T2 and T1 are the transverse and longitudinal relaxation times, respectively—whereas all planar superconducting circuits are sensitive to low frequency noise, such that T2 is often significantly <2T1. Note that our encoding in a four-photon KPO is insensitive to such a noise. This is because the collapse operator that models the dephasing process, \(\sqrt{{\gamma }_{\phi }}{\hat{a}}^{{\dagger} }\hat{a}\), induces population leakage out of the information space (see the section “Photon gain and dephasing” and Fig. 4c) and this process requires an energy greater than the protection energy gap34,38,43,45.

Another relaxation process other than bit and phase flips is population leakage out of the code space. The origin of population leakage to the HEL space is finite-transition probability between the code and HEL spaces—for example, \({\left|\left\langle {0}_{{{{\rm{mod}}}}}^{{{{\rm{h}}}}} \left|\hat{a}\right|{1}_{{{{\rm{mod}}}}}\right\rangle\right|}^{2}=0.073\) and \({\left|\left\langle {2}_{{{{\rm{mod}}}}}^{{{{\rm{h}}}}} \left|\hat{a}\right|{3}_{{{{\rm{mod}}}}}\right\rangle\right|}^{2}=0.029\)—where the lowercase h indicates that the state is a part of the HEL space. By calculating the population of all states, including the HEL space (see Supplementary Table 1), we find that our AQEC scheme is effective in reducing the population of the error space, which is suppressed by more than one order of magnitude after 10 μs (the upper panel of Fig. 2c). The population of the HEL space is also suppressed by 44% at 100 μs. This population leakage has been called quantum heating—a heating process induced by quantum jumps due to dissipation (in this case, single-photon loss) in quasienergy levels of driven quantum nonlinear systems54,62,63,64. The steady-state solution in Supplementary Table 1 is indeed independent of γKPO, which is a signature of quantum heating54,63. The AQEC process does not generate quantum heat because the correction tone is weak and continuous; thus, transitions over the protection gap do not occur. It can be said that AQEC cools quantum heat.

Optimization

A potential problem of our encoding is that the mean photon number of \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\) are 2.9 and 3.8, respectively, thereby suggesting that our logical qubit does not satisfy Knill–Laflamme conditions65,66. One consequence of this is that the probabilities of single-photon loss events in the two logical qubit states are different, thereby resulting in information leakage directly to the environment or indirectly via the ancilla resonator. The information leakage path via the ancilla can be minimized by designing the dispersive shift due to the coupling between the KPO and the ancilla being much smaller than the linewidth of the ancilla. Simultaneously, g must be sufficiently large to generate a reasonably high Acor from the correction tone because Acor is determined by g, although these two are written as independent parameters in Eq. (5). We find that g/2π = 7 MHz used in Fig. 2 meets these criteria (see the end of Supplementary Note 1).

Remarkably, the phase-flip time increases significantly when the four-photon pump amplitude P is slightly higher than the value for energy degeneracy, when g/2π > 4 MHz (Fig. 3a). This slight detuning separates the population peaks of \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\) as depicted in Fig. 3b. We set the frequency at the center of two peaks as the optimal ωcor.

Fig. 3: Optimization procedure.
figure 3

a Upper panel: Four-photon pump amplitude as a function of the KPO–ancilla coupling constant. The solid circle indicates the pump amplitude where the phase-flip time is maximized and the empty triangle indicates the pump amplitude where quasienergy levels are degenerate. Lower panel: Phase-flip time with two different four-photon pump amplitudes. The symbols are the same as those in the upper panel, except the cross symbol indicates the phase-flip time without AQEC. The dashed horizontal line indicates T2 in the \(\left|0\right\rangle\) and \(\left|1\right\rangle\) encoding. The dotted vertical line indicates the coupling constant that we used in this work, g/2π = 7 MHz. b Populations of the logical qubit states as a function of ωcor after 10 μs of evolution with Acor/2π = 0.10 and 0.25 MHz. The arrow indicates the frequency we used as the optimal ωcor. c Bit- and phase-flip times as a function of Acor and γan at the optimal ωcor. The red squares, where the phase-flip time is maximized, indicate the conditions used in Fig. 2.

Full size image

Other parameters, Acor and γan, can be optimized to maximize the bit- and phase-flip times by sweeping the parameter space (Fig. 3c). The reason for existence of the optimal Acor is that if Acor is too large, the height of the peak decreases because the dip becomes broader and eventually undermines the peak, as presented in Fig. 2a.

Photon gain and dephasing

Our AQEC scheme corrects errors induced only by single-photon loss. Thus, it is important to check how other relaxation channels, photon gain and dephasing, degrade our AQEC scheme. Figure 4a and b shows how much the bit- and phase-flip rates increase with thermal photon number nth, which characterizes the photon gain process, and dephasing rate γϕ in Eq. (4). Note that photon gain and dephasing contribute differently to population leakage: photon gain increases populations in both the error and HEL spaces, while dephasing induces population leakage to the HEL space only, as shown in Fig. 4c.

Fig. 4: Effects of single-photon gain and dephasing.
figure 4

a and b Bit- and phase-flip rates as a function of single-photon gain (nth) and dephasing (γϕ). The bit- and phase-flip rates are obtained via the same procedure depicted in Fig. 2b and c. c Population leakage to the error and HEL spaces with AQEC in the presence of single-photon gain and effective dephasing. The solid lines indicate the populations when nth = 0 and γϕ/2π = 0 kHz; the dashed lines, nth = 0.15 and γϕ/2π = 0 kHz; the dash-dot lines, nth = 0 and γϕ/2π = 0.3 kHz. The result in c is the average of two evolutions from \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\); the evolution from \(\left|{+}_{{{{\rm{L}}}}}\right\rangle\) yields similar results.

Full size image

Now, we discuss the upper bounds of nth and γϕ for reliable error correction. According to Fig. 4a, nth must be less than 0.01 to keep the increase in the flip rates <20%. For γϕ, although a four-photon KPO is insensitive to dephasing induced by low-frequency noise as pointed out in the section “Numerical simulation”, the KPO may be exposed to effective dephasing caused by quantum jumps in a nearby quantum system. The rate of such a dephasing process is given by67,68

$${\gamma }_{\phi }=\frac{{\gamma }_{{{{\rm{NQS}}}}}}{2}\mathrm{Re} \,\left[\sqrt{{\left(1+\frac{2{{{\rm{i}}}}\chi }{{\gamma }_{{{{\rm{NQS}}}}}}\right)}^{2}+\frac{8{{{\rm{i}}}}\chi }{{\gamma }_{{{{\rm{NQS}}}}}}{n}_{{{{\rm{th}}}}}^{{{{\rm{q}}}}}}-1\right],$$
(6)

where γNQS and \({n}_{{{{\rm{th}}}}}^{{{{\rm{q}}}}}\) are the damping rate and the thermal photon number of the nearby quantum system, respectively, and χ is the dispersive shift between the KPO and the nearby quantum system. We first consider dephasing induced by the ancilla resonator. In this case, γNQS = γan and \(\chi \equiv K{[g/({\omega }_{{{{\rm{an}}}}}-{\omega }_{{{{\rm{KPO}}}}})]}^{2}\). Even if the thermal photon number of the ancilla is as large as 0.1, γϕ/2π is still <1 Hz, which is completely negligible. Similarly, the partial population of the ancilla resonator during AQEC may be concerning. The mean photon number for this is ~0.02; thus, it is also negligible.

Another possible quantum system that can result in effective dephasing is a transmon or a resonator for readout. Here, we consider a transmon. In this case, χ ≫ γNQS; then Eq. (6) becomes \({\gamma }_{\phi }\approx {n}_{{{{\rm{th}}}}}^{{{{\rm{q}}}}}{\gamma }_{{{{\rm{NQS}}}}}\)69. If T1 of the transmon is 20 μs, \({n}_{{{{\rm{th}}}}}^{{{{\rm{q}}}}}=0.02\) yields γϕ/2π ≈ 160 Hz, where the bit- and phase-flip rates increase significantly (Fig. 4b). Thus, it is crucial to keep the system as cold as possible so that \({n}_{{{{\rm{th}}}}}^{{{{\rm{q}}}}}\ll 0.01\) to maximize the performance of the AQEC scheme70,71.

Unconditional reset

Our simple AQEC scheme is not the only advantage of a four-photon KPO—now, we introduce an unconditional reset scheme that forces the state of the system to evolve to one of the logical qubit states regardless of the initial state. In this scheme, an additional microwave tone is required as well as the correction tone. This additional tone, which we call the reset tone, activates the transitions suppressed by ωgap such that all populations within the information space are transferred to either \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) or \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\), depending on the frequency of the reset tone (Fig. 5a). We simulate this scheme by adding the term \(\hslash {A}_{{{{\rm{reset}}}}}\cos ({\omega }_{{{{\rm{reset}}}}}t)({\hat{a}}^{{\dagger} }{\hat{b}}^{{\dagger} }+\hat{a}\hat{b})\) to Eq. (5), where Areset and ωreset are the amplitude and frequency of this term, respectively.

Fig. 5: Unconditional reset.
figure 5

a Frequencies of the reset/correction tones (upper panel) and population transfer path created by these two tones (lower panel). The reset tone in red and the correction tone in gray lock the system state to \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\), whereas the orange and gray lock the system to \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\) by following the population transfer path. The frequency of the reset tone is determined by the position of the dip in Fig. 2a. b and c Numerical simulation of our reset scheme. The states near the curves indicate the initial states. The insets show the short-time behavior. The parameters for b are as follows: Acor/2π = 0.50 MHz, ωreset/2π = ωcor/2π−12.2 MHz, Areset/2π = 0.32 MHz. The parameters for c are as follows: Acor/2π = 0.45 MHz, ωreset/2π = ωcor/2π + 12.2 MHz, Areset/2π = 0.40 MHz. Other parameters are identical to those for Fig. 2b and c.

Full size image

Figure 5b shows the population of \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) as a function of time when the system is exposed to the correction and the reset tones with ωreset = Δan−ωgap, which locks the system to \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\). Note that, the population of \(\left|{0}_{{{{\rm{L}}}}}\right\rangle\) saturates at about 90% regardless of the initial state. Thus, we can reset the logical qubit simply by applying two microwave tones without any state preparation. If the initial state is in the information space, the KPO state can reach the target state in <5 μs (the inset of Fig. 5b); however, if the initial state is outside of the information space, such as Fock states, the reset might take nearly 100 μs mainly because of the protection energy gap. Reset to \(\left|{1}_{{{{\rm{L}}}}}\right\rangle\) can be carried out by setting ωreset = Δan + ωgap (Fig. 5c).

One may find some similarity between this reset scheme and dynamic nuclear polarization72,73 because the population transfer path in Fig. 5a is identical to that of dynamic nuclear polarization in an interacting nucleus–electron pair of spins 1/2. Transitions from the code space to the error space correspond to the electron spin excitation and transitions within the code space correspond to the nuclear spin excitation. We stress that, however, our scheme is more general than dynamic nuclear polarization because our scheme can reset even a state outside of the information space.

Gate operation and circuit implementation

Thus far, we have focused on error correction and state preparation. In this section, we briefly discuss gate operations and circuit implementation. Since our code relies on the fourfold rotational symmetry, the X gate can be implemented by a two-photon drive with the frequency ωp/2 ± ωgap as shown in Figs. 1b and 2b. QuTiP simulations for X gate operations are presented in Supplementary Fig. 3. The Z gate can be implemented by waiting for the time π/ωgap or by shifting the phase of the subsequent drive (virtual Z gate74,75).

One possible circuit implementation is shown in Fig. 6. Note that we employ two symmetric loops for the KPO. (A similar circuit was used differently in ref. 76.) Because of this symmetry, no current flows through the junction array. Thus, we can separate the system into a weakly nonlinear inductor (junction array) and a symmetric DC SQUID. One consequence of this is that, for KPO1, almost linear modulation of the junction energy can be obtained at Φex1 = 0.5Φ0, which we call the optimal bias. The reason is that the effective junction energy of a symmetric DC SQUID is given by \(2{E}_{{{{\rm{J1}}}}}\cos (\pi {{{\Phi }}}_{{{{\rm{ex1}}}}}/{{{\Phi }}}_{0})\)77, which results in \(-2{E}_{{{{\rm{J1}}}}}\sin (\pi {{{\Phi }}}_{{{{\rm{ac1}}}}}/{{{\Phi }}}_{0})\) at the optimal bias, where Φac1 is an oscillating flux passing through KPO1. Thus, by setting the frequency of Φac1 close to 4ωKPO and 2ωKPO, we obtain the four-photon pump and the two-photon drive from the five- and three-wave mixing, respectively, without having unwanted processes from even terms of Φac1 (see Supplementary Note 1). Another consequence is that the Kerr coefficient is mainly determined by the junction array at the optimal bias. Such a functional separation allows us to design the circuit conveniently.

Fig. 6: Circuit implementation.
figure 6

Here, two KPOs are coupled via a flux-tunable coupler, which is a direct current superconducting quantum interference device (DC SQUID). Two large junctions with vertical dots represent a junction array. The junction capacitances and ancilla resonators are not shown for simplicity.

Full size image

One potential problem regarding actual experiments is that the resulting amplitude of the four-photon pump [P in Eq. (1)] might be too small. We find that P is proportional to KN3 at the optimal bias, where N is the number of Josephson junctions in the junction array (see Supplementary Note 1). Hence, it is advantageous to select N ≫ 1. However, N cannot be arbitrarily large: the capacitive energy of KPO, which is given by KN2, is limited by an intrinsic capacitive energy of a Josephson junction, which is approximately a few GHz. Thus, if the target K is approximately a few tens of MHz, then N cannot exceed 10. One may apply a more advanced technique that was originally developed for a dissipative parametric oscillator to generate higher-order nonlinearity from lower-order parametric processes78,79.

To complete a universal gate set, we need a two-qubit gate. Here, we consider the iSWAP \({\hat{U}}_{{{{\rm{iSWAP}}}}}\) and bSWAP \({\hat{U}}_{{{{\rm{bSWAP}}}}}\) gates, which are defined by80,81

$${\hat{U}}_{{{{\rm{iSWAP}}}}}=\left(\begin{array}{llll}1&0&0&0\\ 0&0&-{{{\rm{i}}}}&0\\ 0&-{{{\rm{i}}}}&0&0\\ 0&0&0&1\\ \end{array}\right),\quad {\hat{U}}_{{{{\rm{bSWAP}}}}}=\left(\begin{array}{llll}0&0&0&-{{{\rm{i}}}}\\ 0&1&0&0\\ 0&0&1&0\\ -{{{\rm{i}}}}&0&0&0\\ \end{array}\right).$$
(7)

The iSWAP gate requires two-photon exchange terms, i.e., \({\hat{a}}_{1}^{{\dagger} }{\hat{a}}_{1}^{{\dagger} }{\hat{a}}_{2}{\hat{a}}_{2}+{\hat{a}}_{1}{\hat{a}}_{1}{\hat{a}}_{2}^{{\dagger} }{\hat{a}}_{2}^{{\dagger} }\), where \({\hat{a}}_{i}\) and \({\hat{a}}_{i}^{{\dagger} }\) are the ladder operators for KPO i (i = 1, 2); the bSWAP gates requires \({\hat{a}}_{1}^{{\dagger} }{\hat{a}}_{1}^{{\dagger} }{\hat{a}}_{2}^{{\dagger} }{\hat{a}}_{2}^{{\dagger} }+{\hat{a}}_{1}{\hat{a}}_{1}{\hat{a}}_{2}{\hat{a}}_{2}\). These terms can be induced without disturbing the optimal bias of each KPO by applying a parametric drive to a tunable coupler80,82. In Fig. 6, a DC SQUID is employed as a tunable coupler. In such a configuration, a parametric drive with the frequency \(2\left|{\omega }_{{{{\rm{KPO1}}}}}-{\omega }_{{{{\rm{KPO2}}}}}\right|\), where ωKPOi is the transition frequency of KPO i, gives the two-photon exchange terms at Φex3 = 0.5Φ0, thus resulting in the iSWAP gate (see Supplementary Note 2). Similarly, a parametric drive with the frequency 2(ωKPO1 + ωKPO2) implements the bSWAP gate at the same flux bias.

Discussion

Here, we list some comments on future research directions. First, the present work is based on numerical analysis. Further general and analytic treatment on the physics underlying this scheme is desirable; in particular, the increase in the phase-flip time due to the detuning of P must be clarified.

Second, a convenient single-shot readout scheme must be developed, such as cat-quadrature readout for cat states in a two-photon KPO38,43,83.

Third, the unconditional reset scheme must be improved to enhance the final population of the target logical state. Since about half of the lost population is in the error space and the other half is in the HEL space (see Supplementary Table 1), we must develop a scheme that transfers the population of the HEL space to the information space without too much cost.

Lastly, a more efficient optimization procedure is required. In this work, the essential parameters, such as the frequency and amplitude of microwave tones as well as the single-photon loss rate of the ancilla, are determined by sweeping the parameter space as shown in Figs. 2a and 3c. One interesting research direction is to combine our schemes and the automation procedure developed in ref. 25.

In summary, we have proposed an AQEC scheme that requires only one continuous microwave tone. This scheme is based on (i) the protection of the information space by applying a four-photon pump to a KPO, (ii) the energy degeneracy between \(\left|{0}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{1}_{{{{\rm{mod}}}}}\right\rangle\) as well as between \(\left|{2}_{{{{\rm{mod}}}}}\right\rangle\) and \(\left|{3}_{{{{\rm{mod}}}}}\right\rangle\), (iii) one-way transition using a lossy ancilla resonator, and (iv) suppressing unwanted transition by creating an energy gap. By solving the master equation, we show that the relaxation times of the logical qubit states surpass the break-even point with our AQEC scheme. In addition to AQEC, we introduce an unconditional reset scheme that lets the system evolve into one of the logical qubit states by simply applying two continuous microwave tones.

Complications in bosonic codes originate from state-by-state control in the Fock basis. This is a consequence of using the dispersive coupling between a bosonic system and a nonlinear ancilla for control84,85. A four-photon KPO can be a radically different approach because its finite anharmonicity allows us to control the system without an ancilla, and the logical qubit states are quasienergy eigenstates such that AQEC and gate operation do not need to rely on the Fock basis. This suggests that we can apply the intuition acquired from conventional two-level-system qubits to a four-photon KPO; the similarity between our reset scheme and dynamic nuclear polarization can be an example of this. Thus, we believe our AQEC and reset schemes reduce hardware overhead significantly, making a KPO an essential unit for future bosonic quantum computing systems.