Introduction

Quantum technologies have the potential to enhance the capability of many applications1 such as sensing2,3,4, communications5,6,7,8, and computation9. Ultimately, a worldwide networked infrastructure of dedicated quantum technologies, i.e. a quantum internet10, could enable distributed quantum sensors11,12,13,14, precise timing and navigation15,16,17, and faster data processing through distributed quantum computing18. This will require the establishment of long distance quantum links at global scale. A fundamental difficulty is exponential loss in optical fibres, which limits direct transmission of quantum photonic signals to < 1000 km19,20,21,22. Quantum repeaters may overcome the direct transmission limit but stringent performance requirements render them impractical by themselves for scaling to the intercontinental ranges needed for global scale-up23. Alternatively, satellite-based free-space transmission significantly reduces the number of ground quantum repeaters required24.

Satellite-based quantum communication has attracted much recent research effort23,24,25,26,27,28,29,30 following recent in-orbit demonstrations of its feasibility by the Micius satellite31. For low-Earth orbit (LEO) satellites, a particular challenge is the limited time window to establish and maintain a quantum channel with an optical ground station (OGS). For satellite quantum key distribution (SatQKD), this constrains the amount of secret key that can be generated due to two issues. First, the commonly assumed asymptotic resource assumption is not a good approximation for short received signal blocks. Without an arbitrarily large number of received signals, statistical uncertainties can no longer be ignored and the security of the distilled secret key requires careful treatment of the statistical fluctuations in estimated parameters32,33,34. Second, the trade-off between the proportion of signals used for parameter estimation and key generation becomes increasingly important to optimise. Further post-processing operations, such as error correction, reduce the amount of extractable secret key, with small block lengths leading to additional inefficiencies over the asymptotic limit35,36.

Initial SatQKD studies used the observed standard deviation to estimate statistical uncertainties and derive correction terms to the secret key rate37,38. Analyses based on smooth entropies32 improve finite-key bounds39 and have been applied to free-space quantum communication experiments40. Recently, tight bounds36 and small block analyses41 further improve key lengths for finite signals. Here, we provide a detailed analysis of SatQKD secret key generation, which utilises tight finite block statistics in conjunction with system design and operational considerations.

As part of our modelling, we implement tight statistical analyses for parameter estimation and error correction to determine the optimised, finite-block, single-pass secret key length (SKL) for weak coherent pulse (WCP) efficient BB84 protocols using three signal intensities (two-decoy states). We base our nominal system model on recent experimental results reported by the Micius satellite42 and use a simple scaling method to extrapolate performance to other SatQKD configurations. The effects of different system parameters are explored, such as varying system link efficiencies, protocol choice, background counts, source quality, and overpass geometries. We also provide a simple estimation method to determine the maximum expected long-term key volume at a particular OGS latitude. The improvement from combining data from multiple satellite passes is also examined. Our model and analysis may guide the design and specification of SatQKD systems, highlighting factors in the quantum communication link that limit secret key generation in the regime of high channel loss and limited pass duration.

We outline the system model in section ‘System model’, including overpass geometries and system parameters. Operational models and finite block construction are given in section ‘SatQKD Operations’. We describe in section ‘Finite key length analysis’ our SatQKD finite key analysis and examine the dependence of the SKL on different system parameters in subsequent sections. We conclude with a discussion of our results in section ‘Discussion’.

Results

System model

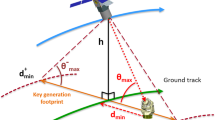
We consider a satellite in a circular Sun-synchronous orbit (SSO) of altitude h = 500 km, similar to the Micius satellite31, performing downlink QKD to an OGS at night to minimise background light. The elevation and range is calculated as a function of time for different overpass geometries representing different ground track offsets and maximum elevations for the overpass (Fig. 1a). The instantaneous link efficiency ηlink is calculated as a function of the elevation θ(t) and range R(t) to generate expected detector count statistics. The quantum link is restricted to be above \({\theta }_{\min }=1{0}^{\circ }\).

Fig. 1: Satellite-to-ground QKD model.
figure 1

a General satellite overpass geometry for circular orbit of altitude h50. Maximum elevation \({\theta }_{\max }\) reached when satellite—OGS ground track distance is at a minimum, \({d}_{\min }\). The smallest \({\theta }_{\max }\), \({\theta }_{\max }^{-}\), that generates finite key defines the key-generation footprint \(2{d}_{\min }^{+}\). b Zenith overpass maximises transmission time with lowest average channel loss. Quantum transmission is limited to above \({\theta }_{\min }\). c Zenith overpass channel loss vs time/elevation (based on ref. 42 data). Link loss varies with range (R−2 diffraction fall-off) and the atmospheric optical depth (attenuation and turbulence). Peak link loss ηlink at zenith characterises the system loss performance level, denoted \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). Additional constant losses (independent of range and elevation) are modelled by constant dB offset to the link loss curve, hence also off-setting \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). d Modelled sifted key rate and QBER vs time/elevation. Zenith overpass, \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=27\) dB, pec = 5 × 10−7, and QBERI = 0.5%. BB84 WCP-DS protocol parameters: fs = 200 MHz, μ1,2,3 = 0.5, 0.08, 0.0, p1,2,3 = 0.72, 0.18, 0.1, with pX = 0.889, 0.9 for the transmitter and receiver basis bias, respectively, as in ref. 45. Shaded region indicates elevation below \({\theta }_{\min }=1{0}^{\circ }\).

Full size image

The link loss \({\eta }_{{{\mbox{link}}}}=-10{\log }_{10}{p}_{{{\mbox{d}}}}\) (dB) is determined by the probability, pd, that a single photon transmitted by the satellite is detected by the OGS. A lower dB value of ηlink represents smaller loss due to better system electro-optical efficiency. This improvement could stem from the use of larger transmit and receive aperture diameters, better pointing accuracy, lower receiver internal losses, and higher detector efficiencies. Internal transmitter losses are not included since they can be countered by adjusting the WCP source to maintain the desired exit aperture intensities37. We also do not explicitly consider time-varying transmittance, modelling the average change in channel loss due only to the change in elevation with time. For discrete variable QKD (DV-QKD) protocols, e.g. BB84, channel transmissivity fluctuations do not directly impact the secret key rate, in contrast to continuous variable QKD where this appears as excess noise leading to key reduction43,44.

The ideal overpass corresponds to the satellite traversing the OGS zenith (Fig. 1b) giving the longest transmission time with lowest average channel loss. Generally, an overpass will not pass directly overhead but will reach a maximum elevation \({\theta }_{\max }( < 9{0}^{\circ })\). We model total losses, including pointing and atmospheric effects, using Micius in-orbit measurements (ref. 42 Extended data, Fig. 3b) to construct a representative ηlink vs θ curve extrapolating over the entire horizon to horizon passage time (Fig. 1c). The Micius data represent a near ideal scenario since the OGSs are situated in dark sky conditions at high altitudes of ~3000 m minimising the effects of atmospheric turbulence and attenuation, other sites may perform differently. Though the link efficiency in ref. 42 is for the entanglement distribution system, not the optimised prepare-measure QKD downlink system as reported in ref. 45, it should still be representative of downlink efficiencies and sifted key rates achievable with current technologies (Fig. 1d).

Systems with higher link losses are also considered. The system loss metric, \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\), is used to characterise the overall system electro-optical efficiency independent of the overpass geometry, and is defined as the ηloss value at zenith, i.e. the maximum probability of detecting a single photon sent from the satellite to the OGS. Worse performing systems have a larger associated \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). The baseline \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) value considered is 27 dB, which corresponds to the improved Micius system using a 1.2 m diameter OGS receiver at Delingha42. By increasing the value of this metric, we explore the performance of SatQKD systems with greater fixed losses, e.g. using a smaller OGS, but otherwise similar behaviour to the Micius system. We consider a maximum \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) value of 40 dB since this reflects realistic SatQKD operation using smaller OGS receiver diameters and a reduced pointing accuracy of smaller satellites. If the time-averaged ground spot is much larger than the OGS diameter Dr, \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) scales as \(20{\log }_{10}({D}_{{{\mbox{r}}}}/{D}_{{{\mbox{r}}}\,}^{0})\) (dB) where \({D}_{\,{{\mbox{r}}}\,}^{0}=1.2\) m is the reference Delingha OGS diameter.

Estimating the effect of transmitter aperture (Dt) is more complex since factors other than diffraction, such as pointing performance and turbulence, also determine the time-averaged ground spot size46,47. Micius, with Dt of 180 mm and 300 mm and sub-μrad pointing performance, reported 10 μrad beam widths42 which suggests the presence of non-diffraction-limited beam spreading effects that may result in a smaller dependence of \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) on Dt. A smaller Dt could result in a smaller increase in \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) than given by purely diffractive beam broadening, conversely using a larger Dt may not significantly improve \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) if pointing and turbulence losses dominate. We refer the reader to detailed analyses of atmospheric turbulence48 or extinction49, and more recent works where their effects on SatQKD are considered46,50,51.

We simplify our model by including several quantities in the parameters pec and QBERI. The sum of dark and background light count rates, pec, is assumed constant and independent of elevation. The intrinsic quantum bit error rate, QBERI, combines errors arising from source quality, receiver measurement fidelity, basis misalignment, and polarisation fluctuations52. Baseline system parameters are summarised in Table 1.

Table 1 Baseline SatQKD system parameters. λEC depends on block size and QBERI = 0.5% is consistent with Micius results19.
Full size table

SatQKD Operations

A standard model of SatQKD uses large, fixed, and long-term OGSs to establish links with satellites29. A more demanding scenario is where the OGS may only be able to communicate sporadically with a particular satellite, limiting the amount of data that can be processed as a single large block, e.g. smaller, mobile OGS terminals may be required to generate a key from a limited number of passes, possibly only one, due to operational constraints. In contrast, fibre-based QKD can often assume a stable quantum channel able to be operated continuously until a sufficiently large block size is attained. High count rates and large block sizes, e.g. 1012, are generally more feasible in fibre-based QKD.

In SatQKD, often the theoretical instantaneous asymptotic key rate \({{{{\mathscr{R}}}}}_{\infty }(t)\) is integrated over the overpass to give the continuous secret key length (SKL)28,29,

$${\,{{\mathrm{SKL}}}}_{\infty }^{{{\mathrm{Cont}}.}}=\int\nolimits_{{t}_{{{\mathrm{start}}}}}^{{t}_{{{\mathrm{end}}}}}\,{{{{\mathscr{R}}}}}_{\infty }(t)dt,$$
(1)

where the quantum transmission occurs between times tstart and tend. Data segments from multiple passes with identical statistics should be combined to yield an asymptotically large block for post-processing. More practically, small blocks, each having similar statistics, from different passes are combined to give the following SKL,

$${\,{{\mathrm{SKL}}}}_{\infty }^{{{\mathrm{Block}}}\,}=\mathop{\sum}\limits_{j}{{{{\mathscr{R}}}}}_{\infty }^{(j)}{{{{\mathcal{L}}}}}_{j},$$
(2)

where \({{{{\mathscr{R}}}}}_{\infty }^{j}\) is the asymptotic key rate for a small segment j, and \({{{{\mathcal{L}}}}}_{j}\) its length. Operationally, this leads to considerable latency between establishing a first satellite-OGS link and the generation of secret keys after a sufficient number of subsequent overpasses. A less restrictive mode of operation is to combine data from multiple passes without segmenting into data blocks with similar statistics, and processing using asymptotically determined or assumed parameters. However, the security guarantee for this procedure requires closer examination.

Here instead, we process overpass data as a single block without segmentation, incorporating finite statistics and uncertainties to maintain high levels of composable security with

$${{{\mathrm{SKL}}}}_{{{\mathrm{finite}}}}={{\mathrm{SKL}}}\,\left(\left\{{n}_{k}^{\mu },{m}_{k}^{\mu }\right\}\right),$$
(3)

where \(\{{n}_{k}^{\mu },{m}_{k}^{\mu }\}\) denote agglomerated observed counts without partitioning into sub-segments (see ‘Methods’ section ‘Finite key analysis for decoy-state BB84’). This is more practical for large constellations28,53 and OGS numbers, obviating the need to track and store a combinatorially large number of link segments until each has attained a sufficiently large block size for asymptotic key extraction. Note that we have the freedom of constructing block sizes in this manner since the security of the distilled finite key remains unaffected. However, an important requirement in finite key analyses is the assumption that each block is randomly sampled at a constant and uniform rate. This requires both the protocol parameters and the fraction of X to Z bases be kept the same. We do not make any assumptions on the underlying statistics for each data block, which are not required to be the same. Instead, we require only information on the count statistics for the entire overpass.

Finite key length analysis

We now quantify SatQKD system performance and SKL generation from different satellite overpasses. We employ the efficient BB84 protocol with weak coherent pulses (WCPs)6 for which tight finite-key security bounds have been derived for one34 and two33 decoy states. The performance of one and two-decoy states is similar, however using two decoy states allows better vacuum yield estimation, useful in high loss operation. We optimise the two-decoy state protocol parameters and the amount of overpass data used in a block to explore the dependence of the single-pass SKL on different variables and derive an expected long term key volume.

The efficient BB84 protocol54 encodes signals in X and Z bases with unequal probabilities pX and 1 − pX, respectively. One basis is used exclusively for key generation and the other only for parameter estimation. We choose to use the error rate of the announced sifted Z basis to bound leaked information from the sifted X basis raw key. Biased basis choice improves the sifting ratio whilst retaining security. In the asymptotic regime, the sifting ratio tends to 1, versus 0.5 for symmetric basis choice (original BB84). This sifting ratio advantage persists in the finite key regime (see section ‘Protocol performance’) resulting in a longer raw sifted key that reduces parameter estimation uncertainties and provides more raw key to distil.

For the two decoy-state WCP BB84 protocol, the sender randomly transmits one of three intensities μj for j ∈ {1, 2, 3} with probabilities pj. For the purposes of the security proof, we assume the intensities satisfy μ1 > μ2 > μ3 = 0. The finite block secret key length is then given by33,

$$\ell =\Bigg\lfloor {s}_{{\mathsf{X}},{\mathsf{0}}}+{s}_{{\mathsf{X}},{\mathsf{1}}}(1-h({\phi}_{{\mathsf{X}}}))-{\lambda}_{{{\mathrm{EC}}}}-6{\log}_{2}\frac{21}{{\epsilon}_{{{\mathrm{s}}}}}-{\log}_{2}\frac{2}{{\epsilon}_{{{\mathrm{c}}}}}\Bigg\rfloor ,$$
(4)

where sX,0, sX,1 and ϕX, are the X-basis vacuum yield, single-photon yield and phase error rates, respectively. In contrast to fibre-optic based systems, the size of the sifted X-basis data block cannot easily be fixed for satellite-based QKD. Instead the number of pulses N sent per pass is determined by the source repetition rate and the time available during a satellite overpass. In the asymptotic sample size limit (Eq. (2)), the X and Z basis data block sizes are straightforwardly determined by N, the pulse detection probability (itself a function of time), and the sifting ratio. However, finitely sized samples generate observed statistics that deviate from asymptotic expectations. Taking this into account can significantly reduce the SKL and we employ correction terms \({\delta }_{{\mathsf{X}}({\mathsf{Z}}),k}^{\pm }\) that relate the expected and observed statistics for bases X(Z) with a k-photon state, using the tight multiplicative Chernoff bound36 (see ‘Methods’ ‘Finite key analysis for decoy-state BB84’ and ref. 55 for software details).

Error syndrome information is publicly announced to perform error correction. The number of bits thus leaked is denoted λEC, and is accounted for during privacy amplification. In the finite key regime, this information leakage has a fundamental upper bound \({\lambda }_{{{\mathrm{EC}}}}\le \log | {{{\mathcal{M}}}}|\), where \({{{\mathcal{M}}}}\) characterises the set of syndromes in the information reconciliation stage35. We use an estimate of λEC that varies with block size (Eq. (9)).

We characterise the reliability and security of the protocol by two parameters, ϵc and ϵs. The protocol is ε = ϵc + ϵs-secure if it is ϵc-correct and ϵs-secret33,56. For the numerical optimisation, we take ϵc = 10−15 and ϵs = 10−9. Conditioned on passing the checks in the error-estimation and error-correction verification steps, an ϵs-secret key of length ℓ can be generated that is secure against general coherent attacks and is universally composable56. This indicates it is not possible for a malicious party to take advantage of changes to any underlying statistics in each data block that may arise due to changes in channel losses in SatQKD.

In the following sections, we highlight constraints arising from the quantum communication link and its implications for system design. It is also important to consider the constraints arising from the classical communication link. This is particularly important for SatQKD operations. We can use our finite key optimiser to provide an estimate for the number of classical bit transmission required in SatQKD for the baseline system parameters summarised in Table 1 with \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=\)40 dB (see ‘Methods’ section ‘Classical communications for SatQKD’).

Transmission time window optimisation

A satellite overpass is limited in duration and experiences highly varying channel loss, hence the expected count rates and QBER will change significantly throughout the pass. The received data obtained from lower elevations will have higher QBER compared to signals sent from higher elevations due to greater losses and the contribution of extraneous counts. This suggests that the SKL that could be extracted could be optimised by truncating poorer quality data from the beginning and end of the transmission period in some circumstances, despite resulting in a shorter raw block57.

Our approach is to first fix the transmission duration and optimise the protocol parameters to use during the pass, then iterate over the window duration to find the highest resulting SKL. We define the transmission time window to run from −Δt to +Δt, where t = 0 represents the time of highest elevation \({\theta }_{\max }\). For each Δt, we find optimum protocol parameters that maximise the SKL extractable from the data block generated within this transmission window. We impose a minimum elevation limit that reflects practicalities such as local horizon visibility and system pointing limitations. Here we use \({\theta }_{\min }=1{0}^{\circ }\) which for a zenith pass limits 2Δt to less than ~440 s.

We show the SKL as a function of Δt for different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) values in Fig. 2. For small \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\), the QBER at low elevations does not rise greatly above QBERI and it is better to construct keys from the greatest amount of data where Δt reaches the maximum allowed by \({\theta }_{\min }\). Conversely, for large \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\), utilising only data from near zenith leads to a longer SKL due to the better average QBER countering both the smaller raw key length and larger statistical uncertainties.

Fig. 2: Secret key length and QBER vs transmission duration.
figure 2

Zenith overpass with different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) (solid lines), QBERI = 0.5%, and pec = 5 × 10−7. Dashed lines represent truncated block QBERs. For each Δt, the SKL extractable from received data within −Δt to +Δt is optimised over protocol parameters. For the better \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) values, increasing Δt beyond 200 s leads to minor SKL improvement. For larger \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\), including data from low elevations is detrimental to the SKL as seen by an increase in the truncated block averaged QBER. The non-smooth QBER appears since it is not the objective function of the optimisation. The shaded region indicates the time when the satellite elevation is lower than \({\theta }_{\min }=1{0}^{\circ }\).

Full size image

SKL system parameter dependence

We now determine the dependence of the SKL on different system parameters, including extraneous counts pec, intrinsic quantum bit errors QBERI, and the source repetition rate fs. The optimised SKL is then determined for different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) that model alternative SatQKD systems that differ from the baseline configuration (Table 1) up to \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=42\) dB, corresponding to Micius transmitting to an OGS with Dr = 21.3 cm, keeping all other system parameters the same.

We first consider how the SKL is affected by pec, which includes both detector dark counts and background light. For DV-QKD, silicon single photon avalanche photodiodes (Si-SPADs) are typically used for visible or near infrared wavelengths and can achieve a dark count rate of a few counts per second with thermoelectric cooling and temporal filtering58. Superconducting nanowire single photon detectors (SNSPDs)59 can offer superior wavelength sensitivity (particularly beyond 1 μm), dark count rate (less than 1 cps), and timing jitter, though at the expense of greater cost, size, weight, and power (SWaP), owing to the need for cryogenic operation. Background light, due to light pollution and celestial bodies (most notably the Moon) is the main constraint to minimising pec60. We have used a simplified model which does not include elevation dependent background light levels (which is highly site dependent). The impact of varying pec on the single overpass (solid), two-pass normalised (dashed), and normalised block asymptotic (dotted) finite SKLs (see ‘Methods’ section ‘Asymptotic key length per pass’) is shown in Fig. 3a. For the finite variants, the SKL is determined using Eq. (3), where data from either one (solid lines) or two (dashed lines) zenith overpasses are processed as a single block. Multiple-pass SKLs are normalised by the number of passes to maintain a fair comparison with the single pass SKL. For each scenario, while extraneous counts increase the vacuum yield \(s_{{\rm{X}},0}\), any addition to the SKL is offset by reductions from worse phase error rates and error correction terms. For example, a factor of 10 increase in pec results in a 40% net reduction to the SKL for \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=27\) dB. The effect of extraneous counts is further compounded for large \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) values and can result in zero SKL due to an excessive QBER.

Fig. 3: SKL with system loss metric.
figure 3

Fixed system parameters were pap = 10−3, \({\theta }_{\min }=1{0}^{\circ }\). In both plots, solid lines represent the optimised SKL with a single zenith overpass, dashed lines represent the two-pass normalised SKL, and dotted lines represent the normalised block asymptotic SKL (see ‘Methods’ section ‘Asymptotic key length per pass’). a SKL dependence on pec with QBERI = 0.5%. The maximum pec represents operation near a full Moon or with severe light pollution. b SKL dependence on QBERI with pec = 5 × 10−7 per pulse.

Full size image

The QBER also suffers from effects such as non-ideal signals, satellite-OGS reference frame misalignment, or imperfect projective measurements by the OGS. We characterise these by an intrinsic system error, QBERI, which is independent of the count rate or channel loss. Figure 3b illustrates the effect of different QBERI on the SKL. We observe that the finite key length is not as susceptible to changes in the QBERI as compared with pec. The relative effects of both pec and QBERI on the SKL is illustrated in Fig. 4 (see also Supplementary Fig. 1). The SKL varies greatly along the pec direction, with zero finite key returned for large pec irrespective of improvements to QBERI. This indicates that improvements to background light suppression and detector dark count over source fidelities and satellite alignment should be prioritised.

Fig. 4: SKL versus pec and QBERI.
figure 4

Single zenith overpass with \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) values: a 27 dB, b 33 dB, c 37 dB, and d 40 dB. The grey region indicates zero SKL.

Full size image

We can estimate the effect of increasing the source rate fs by incorporating a correction factor to \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) for the current results. Since the SKL is a function of \(\{{n}_{k}^{\mu },{m}_{k}^{\mu }\}\), these only depend on the integrated product of the source rate and the link efficiency, with all other system parameters kept the same. Therefore, a 100 MHz source at a given \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) provides the same amount of raw key as a 1 GHz source with a 10 dB larger system loss metric, e.g. corresponding to a three times smaller OGS receiver diameter (Supplementary Fig. 2). This approximation, however, neglects extraneous counts and the resultant instantaneous QBER which is unaffected by the source rate but does depend on \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). Nevertheless, the above heuristic holds provided the contribution of pec to QBER is small and thus SKL is mostly constrained by raw key length and statistical uncertainties.

Practically, the amount of raw key that could be transmitted during an overpass may be limited by the amount of available stored random bits, irrespective of increases in fs. Real-time quantum random number generation can overcome this though at the expense of increased SWaP, which is often constrained on smaller satellites. Even with limits on the amount of raw key available, increasing fs can still be advantageous by compressing the transmission into a smaller duration around \({\theta }_{\max }\), which decreases the average loss per transmitted block.

Protocol parameters that affect the SKL include signal intensities μj, their probabilities pj, and basis bias pX. The optimum values of these system parameters generally depend on \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) and the overpass geometry. The optimal key generation basis choice probability pX decreases with increasing \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). As the OGS detects fewer photons with increasing loss, leading to worse parameter estimation of sX,0, sX,1 and ϕX due to greater statistical fluctuations, to compensate we need to collect more Z basis events by increasing 1 − pX. The reduced number of key generation events is outweighed by better bounds on the key length parameters. This implies that the uncertainties in the parameter estimation from finite statistics dominates the SKL compared with raw key length when \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) is large (Supplementary Fig. 3).

SKL and overpass geometry

A typical satellite overpass will not go directly over zenith but will pass within some minimum ground track offset \({d}_{\min }\) of the OGS, reaching a maximum elevation \({\theta }_{\max }( < 9{0}^{\circ })\) (Fig. 1a). To maximise the number of overpass opportunities that can generate a secret key, a SatQKD system should be able to operate with as low a maximum elevation \({\theta }_{\max }\) as possible. The SKL per pass as a function of \({d}_{\min }\) is shown in Fig. 5 for different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) values. As expected, overpasses with smaller \({\theta }_{\max }\) deliver smaller SKLs due to shorter transmission times and lower count rates from large average ηlink at lower elevations and longer ranges. The SKL vanishes once \({\theta }_{\max }\) is below a critical elevation angle \({\theta }_{\max }^{-}\) when the small block size leads to excessive statistical uncertainties or the average QBER becomes too high.

Fig. 5: SKL vs ground track off-set.
figure 5

pec = 5 × 10−7 and QBERI = 0.5%. The key generation footprint is given by the maximum \({d}_{\min }\) with non-zero SKL. Solid lines correspond to imposing \({\theta }_{\min }=1{0}^{\circ }\) (indicated by dark grey region on the right) and dashed lines to no elevation limit. The shaded areas under the curves determine the expected annual SKL for different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). Imposing \({\theta }_{\min }=1{0}^{\circ }\) reduces the area, and hence the expected annual SKL, by 18.82%, 13.37%, and 3.58% at 27 dB, 30 dB, and 33 dB, respectively.

Full size image

We now can estimate the long-term average amount of secret key that can be generated using single overpass blocks with an OGS site situated at a particular latitude. We first integrate the area under the SKL vs \({d}_{\min }\) curve,

$${{{\mathrm{SKL}}}}_{{{\mathrm{int}}}}=2\int\nolimits_{0}^{{d}_{\min }^{+}}{{{\mathrm{SKL}}}}_{{d}_{\min }}\ d{d}_{\min },$$
(5)

where \({d}_{\min }^{+}\) is the maximum OGS ground track offset that generates key. Assuming a sun synchronous orbit, we then estimate the expected annual key from (neglecting weather),

$${\overline{{{\mathrm{SKL}}}}}_{{{\mathrm{year}}}}={N}_{{{\mathrm{orbits}}}}^{{{\mathrm{year}}}}\frac{{{{\mathrm{SKL}}}}_{{{\mathrm{int}}}}}{{L}_{{{\mathrm{lat}}}}},$$
(6)

where \({N}_{\,{{\mathrm{orbits}}}}^{{{\mathrm{year}}}\,}\) is the number of orbits per year, and Llat is the longitudinal circumference along the line of latitude at a single OGS location (see Methods section ‘Expected annual SKL’). This estimate assumes that \({d}_{\min }\) is evenly distributed (unless in an Earth synchronous orbit28) and the OGS is not close to the poles where the orbital inclination (~97°) invalidates the approximation of even distribution. In Table 2, we summarise the expected yearly secret finite key lengths attainable for various \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) at latitude 55. 9∘ N.

Table 2 Expected annual SKL for different \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\). The SKLint values correspond to the area under each SKL vs \({d}_{\min }\) curve in Fig. 5 with units of bit-metres (bm).
Full size table

Multiple satellite passes

Disregarding latency of key generation, data from several overpasses can be combined to improve SKL generation. Figure 3 displays finite and asymptotic SKLs for a single zenith overpass. The overpass-normalised asymptotic SKL corresponds to multiple overpasses where the block sizes used for key rate determination tend to infinity. Instead of Eq. (2), we aggregate data from separate overpasses (with the same geometry and protocol parameters) into a single processing block without segmented instantaneous asymptotic key rates, only assuming asymptotically ascertained combined block parameters. The process of taking the block size to infinity requires care due to the limited amount of data per pass (see ‘Methods’ section ‘Asymptotic key length per pass’). The per-pass SKL increases significantly as the block asymptotic regime is approached.

Systems with zero single-overpass SKL can generate positive key by accumulating signals from several overpasses (Fig. 6). If ℓM is the total SKL generated from M identical satellite passes, then ℓM ≥ Mℓ1 with diminishing improvement ℓM+1 − ℓM with increasing M, with the largest jump going from M = 1 to 2. Averaging over several identical passes does not improve the underlying block averaged signal parameters such as QBER, hence the per-pass SKL improvement is mainly due to smaller estimation uncertainties from increased sample size, with better error correction efficiency and reduced λEC also contributing. This shows that finite statistical fluctuations are the principle limitation to the SKL that can be generated with a limited number of overpasses.

Fig. 6: Per-pass SKL vs Number of combined overpasses.
figure 6

Secret key is generated from combined multiple overpass data. Zenith overpasses with \({\theta }_{\min }=1{0}^{\circ }\). System parameter sets \(\{{\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}},{p}_{{{\mathrm{ec}}}},{{{\mathrm{QBER}}}}_{{{\mathrm{I}}}}\}\): A = {45.7 dB, 10−7, 0.5%}, B = {44.8 dB, 10−7, 1%}, and C = {40.5 dB, 5 × 10−7, 1%}.

Full size image

Practically, employing multiple passes to improve SKL generation should be balanced against greater latency and potential security vulnerabilities in storing large amounts of raw data for a longer period between passes. This will depend on the assumed security model and anticipated attack surfaces of the encryption keys at rest61.

Protocol performance

The choice of QKD protocol can also significantly affect the SKL due to finite block size statistics. This is illustrated by comparing two BB84 variants: efficient BB84 (considered thus far)54 and standard BB8462. The main difference is the basis choice bias, with standard BB84 choosing both X and Z bases with equal (symmetric) probability, while efficient BB84 allows biased (asymmetric) basis choice. Standard BB84 also uses both bases to generate key, hence requires parameter estimation of both. Efficient BB84 uses only one basis for key generation and the other for parameter estimation. We refer to the two protocols as s-BB84 and a-BB84, respectively.

In general a-BB84 produces higher SKL for all system loss metrics, can tolerate larger \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\), and operate with lower \({\theta }_{\max }\) (Supplementary Fig. 4). The expected annual SKL (as in section ‘SKL and overpass geometry’) with a-BB84 and s-BB84 for the baseline system parameters (Table 1) is obtainable from Fig. 7. For \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=33\) dB and 40 dB, a-BB84 generates 70% and 182% times more key on average, respectively. The advantage increases with larger \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}\) due to several reasons. First, the better sifting ratio of a-BB84 results in more raw bits that also allows for better parameter estimation. Second, a-BB84 uses all events in one basis to estimate the vacuum and single photon yields in the other. In contrast, s-BB84 reveals an optimally sized random sample of results for each basis to separately estimate signal parameters. Hence only half the revealed results are used for each basis estimation, leading to worse statistical uncertainties.

Fig. 7: Protocol effect on SKL vs ground track offset.
figure 7

Shown are a-BB84 (solid lines) and s-BB84 (dashed lines) with pec = 5 × 10−7, QBERI = 0.5%.

Full size image

A tangential advantage is that a-BB84 requires less classical communication than s-BB84. In a-BB84 the choice of bits for public comparison for QBER estimation is implicit in the basis choice and automatically revealed during sifting. A minor disadvantage to a-BB84 is the extra overhead in generating biased basis probabilities63, but the advantage of s-BB84 in this regard is relatively small taking into account all the biased probabilities required for both decoy-state variants.

Discussion

Important differences with fibre-based QKD mean that small sample statistical uncertainties have a significant impact on the performance of satellite QKD. The restricted overpass time of a LEO satellite constrains the amount of sifted key that can be established with an optical ground station. Operationally, a secret key may need to be generated from a single pass, thus statistical uncertainties will significantly impact performance in practical scenarios. Our study examines the severity of finite-key effects for representative space-ground quantum channel link efficiencies as indicated by the in-orbit demonstration of Micius.

Our results highlight the influence of system and protocol parameters on the secret key length that can be generated from a single overpass. For the range of system loss metrics considered (\({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=27\,\,{{\mbox{to}}}\,\,42\) dB), the strongest dependence comes from the degree by which extraneous counts (pec) can be suppressed, with a much weaker dependence on the intrinsic signal/measurement quality (QBERI) of the system. There is also a minimal effect of imposing a minimum elevation limit for quantum signal transmission. This suggests that SatQKD systems should prioritise background light suppression over higher intrinsic quantum signal visibilities or extending transmission closer to the horizon.

The dominance of finite-key effects is highlighted by the comparison between efficient (asymmetric basis bias) BB84 with conventional (symmetric basis bias) BB84. The much greater secret key length of efficient BB84 stems from a better sifting ratio and longer raw key length as well as obviating the need to perform parameter estimation for two bases that would further compound the finite statistical uncertainty. This greater performance translates into a higher secret key length for a given overpass geometry and also extends the satellite ground footprint within which secret key can be established with a ground station. Overall, improvements in system performance, whether through better protocols, smaller system loss metrics, or higher source rates, can significantly expand expected annual secret key volumes, e.g. a reduction of 3 dB in the system loss metric from 40 dB to 37 dB improves the expected annual key volume by a factor of 7.6. Should operations allow, secret key extraction efficiency can also be enhanced by combining data blocks from several passes, especially if no secret is possible from a single overpass.

This preliminary study of SatQKD finite-key effects can be extended to remove some simplifications and approximations. An immediate extension would include a more comprehensive time and elevation dependent quantum channel model incorporating scattering, turbulence, and anisotropic background light distributions. Site dependent scenarios could include local horizon limits, light pollution, and seasonal weather effects. We can constrain the optimisation of the protocol parameters to reflect additional restrictions on system operations and deployment in practice. Ultimately, design and optimisation of SatQKD systems should incorporate orbital modelling of constellations and ground stations geographic diversity together with cost/performance trade-off studies.

Methods

Finite key analysis for decoy-state BB84

The Bennett-Brassard 1984 (BB84) quantum key distribution (QKD) protocol is widely implemented owing to its simplicity, overall performance and provable security62. However, practical implementations of BB84 depart from the use of idealised single-photon sources. Instead, weak pulsed laser sources are used given their wide availability and relative ease of implementation. This improves repetition rates over current single photon sources, but leaves the BB84 protocol vulnerable to photon-number-splitting (PNS) attacks that exploit the multi-photon pulse fraction present in emitted laser pulses64.

Decoy-state protocols circumvent PNS attacks and improve tolerance to high channel losses, with minimal modification to BB84 implementations. These protocols employ multiple phase randomised coherent states with differing intensities that replace signal pulses. This modification permits better characterisation of the photon number distribution of transmitted pulses associated with detection events65, which reliably detect the presence of PNS attacks in the quantum channel. Decoy-state BB84 protocols also allow better estimation of the secure fraction of the sifted raw key (vacuum and single photon yields), which makes them a secure and practical implementation of QKD.

The security of decoy-state QKD was initially developed assuming the asymptotic-key regime66,67. For applications with finite statistics, uncertainties in the channel parameters cannot be ignored68,69,70. Early approaches in handling these finite key statistics used Gaussian assumptions to bound the difference between the asymptotic and finite results71. This restricts the security to collective and coherent attacks. Security analyses for more general attacks have also been developed72. The multiplicative Chernoff bound39,71 and Hoeffding’s inequality33 can be used to bound the fluctuations between the observed values and the true expectation value. Recently, a more complete finite-key analysis for decoy-state based BB84, with composable security, has been presented in ref. 36, which uses the multiplicative Chernoff bound to derive simple analytic expressions that are tight.

Due to limited transmission times, satellite-based quantum communications are strongly affected by finite statistics. To model different SatQKD systems, we improve the analysis in ref. 33 with recent developments in modelling statistical fluctuations arising from finite statistics. This improvement leads to a more robust SKL and is imprinted through the finite statistic correction terms \({\delta }_{{\mathsf{X(Z)}},k}^{\pm }\), which we define using the inverse multiplicative Chernoff bound36,71. Specifically, let Y denote a sum of M independent Bernoulli samples, which need not be identical. Denote y∞ as the expectation value of Y, with y the observed value for Y from a single experimental run. The magnitude of difference between the observed and expected values depends on the statistics available. To quantify this deviation, we determine the probability that \(y\le {y}^{\infty }+{\delta }_{Y}^{+}\) is less than a fixed positive constant ε > 0, and the probability that \(y\ge {y}^{\infty }-{\delta }_{Y}^{-}\) is less that ε. This is achieved through setting

$${\delta }_{Y}^{+}=\beta +\sqrt{2\beta y+{\beta }^{2}},\quad {\delta }_{Y}^{-}=\frac{\beta }{2}+\sqrt{2\beta y+\frac{{\beta }^{2}}{4}},$$
(7)

where \(\beta =\ln (1/\varepsilon )\)36. Hence, we define the following finite sample size data block size

$$\begin{array}{lll}{n}_{{\mathsf{X(Z)}},k}^{\pm }&=&\frac{{{{{\rm{e}}}}}^{k}}{{p}_{k}}\left[{n}_{{\mathsf{X(Z)}},k}\pm {\delta }_{{n}_{{\mathsf{X(Z)}},k}}^{\pm }\right],\\ {m}_{{\mathsf{X(Z)}},k}^{\pm }&=&\frac{{{{{\rm{e}}}}}^{k}}{{p}_{k}}\left[{m}_{{\mathsf{X(Z),k}}}\pm {\delta }_{{m}_{{\mathsf{X(Z)}},k}}^{\pm }\right],\end{array}$$
(8)

for the number of events and errors respectively in the X(Z) basis. From this, we define the vacuum and single photon yields, and the phase error rate of single-photon events using ref. 33 (see also pseudocode 1 in Fig. 8) that determines the finite key length.

Fig. 8: Pseudocode for the optimised finite key length.
figure 8

We consider a pulse repetition rate fs, M satellite passes in the plane offset by angle ξ from the zenith plane, and time dependent losses L. An elevation constraint of \({\theta }_{\min }=1{0}^{\circ }\) imposes realistic local constraints of establishing an optical link between the OGS and satellite. The key length is optimised over all protocol parameters and a transmission time window Δt over which the raw key is acquired. The correction terms \({\delta }_{{\mathsf{X}}({\mathsf{Z}}),k}^{\pm }\) for bases X(Z) and the intensities μk are determined from the multiplicative Chernoff bound that account for finite statistics36.

Full size image

An important step in any QKD protocol is error correction. This necessitates classical communication, of λEC bits, which are assumed known to Eve. This must be taken account of in the privacy amplification stage. While λEC is known for practical implementations of the protocol, it must be estimated for the finite key optimisation. An overly conservative estimate would yield no key in a region of the parameter space where one should be viable. Conversely, an overly optimistic value for λEC leads to spurious results. This highlights the importance of choosing a good estimate. It is standard to model the channel as a bit-flip channel33,35. This leads to \(\lambda_{\rm{EC}}=f_{\rm{EC}}n_{\mathsf{X}}h_{2}(Q)\), where Q is the QBER and fEC the reconciliation factor. The value for fEC is chosen slightly above unity, e.g. 1.16. The use of a constant reconciliation factor is a simple way of accounting for inefficiency in the error correction protocol. This approach is normally sufficient when determining the optimal secret key length. However, for satellite QKD, one operates with high losses that are at the limit of where one can extract a key. As such, it is beneficial to use a more refined estimate of λEC.

A better estimate for λEC is given in ref. 35. In this approach, the correction to \(n_{\mathsf{X}}h(Q)\) depends on the data block size. In particular,

$$\begin{array}{lll}{\lambda }_{{{\mathrm{EC}}}}={n}_{{\mathsf{X}}}h(Q)+{n}_{{\mathsf{X}}}(1-Q)\log \left[\frac{(1-Q)}{Q}\right]\\ \qquad\quad-\,\left({F}^{-1}({\epsilon }_{{{\mathrm{c}}}};{n}_{{\mathsf{X}}},1-Q,)-1\right)\log \left[\frac{(1-Q)}{Q}\right]\\ \qquad\quad-\,\frac{1}{2}\log ({n}_{{\mathsf{X}}})-\log (1/{\epsilon }_{{{\mathrm{c}}}}),\end{array}$$
(9)

where nX is the data block size, Q is the QBER and F−1 is the inverse of the cumulative distribution function of the binomial distribution. We utilise this definition to estimate the information leaked during error correction in the finite key regime.

These post-processing terms define the attainable finite key, subject to rigorous statistical analyses. The key length is a function of the basis encoding probability, \(p_{\mathsf{X}}\), the source intensities and their probabilities, {μj, pj} for j ∈ {1, 2, 3}, and the transmission time window, Δt, used to construct block data for a satellite pass. Without loss of generality, we set the second decoy state intensity as the vacuum μ3 = 0. For a defined SatQKD system, we generate an optimised finite key length by optimising over the parameter space of the six variables: {pX, μ1, μ2, p1, p2, Δt}. A baseline for system performance used in this work is detailed in Table 1 in the main text. This procedure can be generalised for any satellite trajectory. Fig. 8 illustrates a pseudocode of our numerical optimiser, which is available as open source software55.

Asymptotic key length per pass

In this section, we provide an operational definition for the asymptotic key length per pass and explain how it can be determined by adapting the finite key optimiser. Data is combined from multiple satellite passes. The optimisation over the protocol parameters is then performed on the combined results and a secret key is extracted. For the following, we assume that each satellite pass has the same trajectory. With minimal modification, this can be extended to varying satellite trajectories for each pass.

Denoting ℓM as the SKL attained from M satellite passes, we saw in Fig. 6 that ℓM ≠ Mℓ1. We also saw that the improvement to the SKL decreased with increasing number of satellite passes. This leads to a natural question: what is the largest attainable SKL per pass? This is given by the asymptotic secret key length \({\ell }_{\infty }=\mathop{\lim }\limits_{M\to \infty }{\ell }_{M}/M\). The key length, ℓM, is found using equation (4), and the quantity ℓ∞ is determined by examining the asymptotic scaling of ℓM/M.

The estimate for the vacuum counts per pass is33,

$$\frac{{s}_{{\mathsf{X,0}}}}{M}=\frac{{\tau }_{0}}{{\mu }_{2}-{\mu }_{3}}\frac{{\mu }_{2}{{{\Gamma }}}_{3}({n}_{{\mathsf{X,3}}}-{\delta }_{{\mathsf{X}},3}^{-})-{\mu }_{3}{{{\Gamma }}}_{2}({n}_{{\mathsf{X}},2}+{\delta }_{{\mathsf{X}},2}^{+})}{M},$$
(10)

where nX,k is the number of sifted counts in the X-basis, from pulses of intensity k, τ0 is averaged probability that a vacuum state is transmitted by the laser, \({{{\Gamma }}}_{k}=\exp ({\mu }_{k})/{p}_{k}\) and \({\delta }_{{\mathsf{X}},k}^{\pm }\) are correction terms that account for the finite statistics. In ref. 33, \({\delta }_{{\mathsf{X}},k}^{\pm }\) is derived from Hoeffding’s inequality. A higher SKL is attained by instead deriving these correction terms from the multiplicative Chernoff bound36. The asymptotic scaling of these correction terms are \({{{\mathcal{O}}}}(\sqrt{{n}_{{\mathsf{X}}}})\). This scaling is independent of whether the Hoeffding and Chernoff bounds are used. This scaling implies that the scaling with the number of satellite passes is \({{{\mathcal{O}}}}(\sqrt{M})\). Hence, \({\delta }_{{\mathsf{X}},k}^{\pm }/M\) scales \({{{\mathcal{O}}}}(1/\sqrt{M})\) and thus tends to zero as M → ∞. The finite statistics correction terms thus go to zero, as expected.

Since each satellite pass is assumed to have the same orbit, the total number of counts accumulated \(n_{{\mathsf{X}},k}\) is equal to M times the corresponding number of counts for a single pass, \({n}_{{\mathsf{X}},k}^{(1)}\). From this, we obtain

$$\mathop{\lim }\limits_{M\to \infty }\frac{{s}_{{\mathsf{X,0}}}}{M}=\frac{{\tau }_{0}}{{\mu }_{2}-{\mu }_{3}}\left({\mu }_{2}{{{\Gamma }}}_{3}{n}_{{\mathsf{X,3}}}^{(1)}-{\mu }_{3}{{{\Gamma }}}_{2}{n}_{{\mathsf{X}},2}^{(1)}\right)={s}_{{\mathsf{X}},0}^{\infty },$$
(11)

where \({s}_{{\mathsf{X}},0}^{\infty }\) is the asymptotic estimate of the vacuum counts for a single pass, which we define formally in the next paragraph. By following a similar process for each term in ℓM/M, we obtain

$${\ell }_{\infty }=\lfloor {s}_{{\mathsf{X}},0}^{\infty }+{s}_{{\mathsf{X}},1}^{\infty }\left(1-h({\phi }_{{\mathsf{X}}}^{\infty })\right)-{\lambda }_{\,{{\mbox{EC}}}\,}^{\infty }\rfloor ,$$
(12)

where \({\phi }_{{\mathsf{X}}}^{\infty }={\nu }_{{\mathsf{Z}},1}^{\infty }/{s}_{{\mathsf{Z}},1}^{\infty }\) is the phase error rate, \({s}_{{\mathsf{X}},1}^{\infty }\), \({s}_{{\mathsf{Z}},1}^{\infty }\) and \({\nu }_{{\mathsf{Z}},1}^{\infty }\) are the single pass asymptotic estimates for: the single photon counts in the X basis, the Z basis, and the single photon errors in the Z basis, respectively.

The asymptotic quantities: \({\nu }_{{\mathsf{Z}},1}^{\infty }\), \({s}_{{\mathsf{X}},0}^{\infty }\) and \({s}_{{\mathsf{X(Z)}},1}^{\infty }\), correspond to averaging the single pass quantities over infinitely many passes. More formally, let \(u \in \{\phi_{\mathsf{X}}, \nu_{{\mathsf{Z}},1},s_{{\mathsf{X}}({\mathsf{Z}}),0},s_{{\mathsf{X}}({\mathsf{Z}}),1},\lambda_{\rm{EC}}\}\), and let u(M) denote the quantity estimated using the full data from M passes. The asymptotic quantity is then defined as

$${u}^{\infty }=\mathop{\lim }\limits_{M\to \infty }\frac{{u}^{(M)}}{M}.$$
(13)

A refined estimate of λEC and its upper bound on the asymptotic behaviour is provided in ref. 35. From this, we determine that \({\lambda }_{\,{{\mathrm{EC}}}\,}^{\infty }={n}_{{\mathsf{X}}}^{(1)}h(Q)\), where Q is the QBER for a single pass. When running the finite key optimiser for the asymptotic key length per pass, we define \({\lambda }_{\,{{\mathrm{EC}}}\,}^{\infty }=1.16{n}_{{\mathsf{X}}}^{(1)}h(Q)\), which accounts for inefficient error correction even in the asymptotic limit.

Rather than looking at the key length per pass, it is also common to consider the key rate, i.e. the number of secret key bits per transmitted pulse. Let N be the total number of pulses transmitted by the satellite during a single pass. The key rate for M passes is just SKRM = ℓM/(MN). In the limit of infinitely many passes, the asymptotic key rate is given by SKR∞ = ℓ∞/N.

Notice that our analysis of the asymptotic secret key rate, SKR∞ differs from the route often taken in the literature. Specifically, the asymptotic key rate can be determined as a function of different elevation angles. The data is then combined according to Eq. (1). While such an approach is possible if we extract keys for each angle of elevation, it is not appropriate for the current analysis, where we group all the data for a pass and then extract a key from the combined data.

Classical communications for SatQKD

In traditional fibre-based QKD, the cost of classical communications is often overlooked given the availability of the internet backbone. However, in SatQKD classical radio communications is often constrained due to restrictions in antenna size and power, and thus could possibly represent a bottleneck in the reconciliation process.

We estimate the classical communication capacity required for secret key generation in SatQKD. Using the baseline system parameters from Micius summarised in Table 1, we consider a system loss metric of \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=40\) dB for a zenith pass. For BB84 there are five stages requiring four distinct rounds of classical communication between the satellite (Alice) and the OGS (Bob) to process a block:

  1. 1.

    Alice to Bob: Prior to any classical transmission, Alice first encodes information in the polarisation basis of WCPs that are transmitted to Bob. Based on our finite key optimiser, the optimal time window for \({\eta }_{{{{\rm{loss}}}}}^{{{{\rm{sys}}}}}=\) 40 dB is a total of 200 s centred at zenith (Δt = 100 s) with signal parameters of μ1 = 0.697364, p1 = 0.738668, μ2 = 0.159325, p2 = 0.189355, μ3 = 0, p3 = 0.0720, and a basis encoding probability PX = 0.725313. This results in the expected detections by Bob of \({\overline{n}}_{{\mathsf{X}}}=536038\) and \({\overline{n}}_{{\mathsf{Z}}}=203006\) in the X and Z bases, respectively.

  2. 2.

    Bob to Alice: Bob needs to report to Alice the time-slot positions and basis values for each detection event. To specify a time-slot position requires a maximum of \(\lceil {\log }_{2}(2{{\Delta }}t{f}_{{{\mbox{s}}}})\rceil =36\) bits with a naïve encoding. Bob detected \({n}_{{{\mbox{B}}}}={\overline{n}}_{{\mathsf{X}}}+{\overline{n}}_{{\mathsf{Z}}}=739044\) events and uses 36 + 1 bits per event in his bit string which is < 27 Mb.

  3. 3.

    Alice to Bob: Alice confirms to Bob the time-slot of the detected events for which the bases matched. She also transmits along with each reconciled event the intensity of the pulse (2 bits), and if sent in the Z basis (1 bit), the sent bit value. After basis reconciliation there are on average nX = 388795, nZ = 55763 events in the X and Z bases, respectively. Alice reports nA = nX + nZ = 444558 events and uses at most 36 + 2 + 1 bits per event in her bit string which results in < 20 Mb data to be downlinked.

  4. 4.

    Bob to Alice: Bob now calculates the phase and bit error rates using Alice’s reconciliation data and then transmits to Alice the parameters for the error correction code to use, e.g. which pre-agreed set of low density parity check (LDPC) codes to use, as well as the dimensions of the privacy amplification matrix, which require bit strings of size ≪ 1 kb.

  5. 5.

    Alice to Bob: Alice calculates the specified error correction syndromes and transmits the results to Bob who then performs the error correction on his side. We estimate the amount of syndrome data to be transmitted by the amount of leaked information, λEC = 55360 bits, hence Alice sends < 60 kb down to Bob in this step.

The total classical communication required in the above steps is less than 50 Mb (6.25 MB), of which ~27 Mb is uplinked and ~20 Mb is downlinked.

Note for the classical communication exchange in satellite QKD, steps two and three can start as soon as Bob starts receiving counts. However, steps four and five can only occur after Bob receives the final counts that make up the block, but the amount of data in these steps is minimal. This indicates that the bulk of the classical communication exchange can occur in parallel to the quantum transmission.

Expected annual SKL

We can estimate the expected annual secret key length from SKL vs ground track offset relation. Consider a satellite in sun synchronous orbit (SSO) at an inclination of ~98∘. For OGS latitudes below 60∘, this can be approximated by a polar orbit (Fig. 9). The precession period of a SSO is one year, during which time the satellite makes ~5500 orbits.

Fig. 9: Satellite key generation footprint.
figure 9

We consider a satellite in SSO with inclination 98°. The width of the striped purple arrow underneath the satellite orbit in the longitudinal direction defines the operational key generation footprint for a SatQKD system. For a near polar orbit, the density of satellite overpasses over high latitude locations is larger and hence the annual SKL is enhanced.

Full size image

The striped purple ground path below the satellite is the key generation footprint. As the Earth rotates daily under the orbit of the satellite, the key generation footprint intercepts the line of latitude uniformly on average throughout the year. Note, this is under the assumption that the orbital period is not rationally related to the length of the solar day, i.e. not for a simultaneous SSO and Earth synchronous orbit. Since at low latitudes the distance around the line of latitude is greater than for higher latitudes, the key generation footprint represents a smaller fraction of the longitudinal circumference. Hence, on average, the satellite is more likely to pass close to the OGS at higher latitudes.