Abstract
Distributed quantum information processing is essential for building quantum networks and enabling more extensive quantum computations. In this regime, several spatially separated parties share a multipartite quantum system, and the most natural set of operations is Local Operations and Classical Communication (LOCC). As a pivotal part in quantum information theory and practice, LOCC has led to many vital protocols such as quantum teleportation. However, designing practical LOCC protocols is challenging due to LOCC’s intractable structure and limitations set by near-term quantum devices. Here we introduce LOCCNet, a machine learning framework facilitating protocol design and optimization for distributed quantum information processing tasks. As applications, we explore various quantum information tasks such as entanglement distillation, quantum state discrimination, and quantum channel simulation. We discover protocols with evident improvements, in particular, for entanglement distillation with quantum states of interest in quantum information. Our approach opens up new opportunities for exploring entanglement and its applications with machine learning, which will potentially sharpen our understanding of the power and limitations of LOCC. An implementation of LOCCNet is available in Paddle Quantum, a quantum machine learning Python package based on PaddlePaddle deep learning platform.
Similar content being viewed by others
Introduction
In the past few decades, quantum technologies have been found to have an increasing number of powerful applications in areas including optimization1,2, chemistry3,4, security5,6, and machine learning7. To realize large-scale quantum computers and deliver real-world applications, distributed quantum information processing will be essential in the technology road map, where quantum entanglement and its manipulation play a crucial role.
Quantum entanglement is central to quantum information by serving as a fundamental resource which underlies many important protocols such as teleportation8, superdense coding9, and quantum cryptography6. To achieve real-world applications of quantum technologies, protocols for manipulating quantum entanglement are essential ingredients, and it will be important to improve existing methods. The study of entanglement manipulation is one of the most active and important areas in quantum information10,11.
In entanglement manipulation and distributed quantum information processing, multiple spatially separated parties are usually involved. As direct transfers of quantum data between these nodes are not feasible with current technology, Local Operations and Classical Communication (LOCC)8 is more practical at this stage. Such an LOCC (or distant lab) paradigm plays a fundamental role in entanglement theory, and many important results have been obtained within this paradigm11. However, how to design LOCC protocols on near-term quantum devices12 remains an important challenge. Such protocols are generally hard to design even with perfect entanglement due to the complicated and hard-to-characterize structure of LOCC13. Moreover, limited capabilities and structure of near-term quantum devices have to be considered during the design of LOCC protocols.
Inspired by the breakthroughs of deep learning14 in mastering the game of Go15 and solving protein folding16, it is desirable to apply machine learning ideas to explore quantum technologies. For instance, machine learning has been applied to improve quantum processor designs17,18,19,20 and quantum communication21,22. Here, we adopt the ideas from machine learning to solve the challenges in exploring LOCC protocols. We use parameterized quantum circuits (PQCs)23 to represent the local operations allowed in each spatially separated party and then incorporate multiple rounds of classical communication. Then one can formulate the original task as an optimization problem and adopt classical optimization methods to search the optimal LOCC protocol. The PQCs have been regarded as machine learning models with remarkable expressive power, which leads to applications in quantum chemistry and optimization23. Here, we generalize PQC to a larger deep learning network to deal with distributed quantum information processing tasks and in particular to explore better entanglement manipulation protocols.
In this work, we introduce a machine learning framework for designing and optimizing LOCC protocols that are adaptive to near-term quantum devices, which consists of a set of PQCs representing local operations. As applications, we explore central quantum information tasks such as entanglement distillation, state discrimination, and quantum channel simulation. We discover protocols with evident improvements via this framework, sharpening our understanding of the power and limitations of LOCC. As showcases, we establish hardware-efficient and simple protocols for entanglement distillation and state discrimination, which outperforms previously best-known methods. In particular, for distillation of Bell states with non-orthogonal product noise, the optimized protocol outputs a state whose distillation fidelity even reaches the theoretical upper bound and hence is optimal.
Results
The LOCCNet framework
In this section, we introduce LOCCNet, a machine learning framework that facilitates the design of LOCC protocols for various quantum information processing tasks, including entanglement distillation24,25,26,27,28,29, quantum state discrimination30,31,32,33,34,35,36,37,38,39,40,41, and quantum channel simulation42,43,44,45,46,47,48. An LOCC protocol can be characterized as a sequence of local quantum operations performed by spatially separated parties with classical communication of measurement outcomes [see Supplementary Note 1].
According to the number of classical communication rounds, one can divide LOCC into different classes13. The one-round protocols correspond to LOCC operations where one party applies a local operation and sends the measurement outcome to others, who then apply local operations chosen based on the outcome they receive. Based on one-round protocols, we are able to construct an r-round protocol recursively. All these protocols belong to the finite-round LOCC class, and can be visualized as tree graphs. Each node in the tree represents a local operation and different measurement outcomes correspond to edges connecting to this node’s children, which represent different choice of local operations based on the measurement outcomes from last round.
Although the basic idea of LOCC is relatively easy to grasp, its mathematical structure is highly complicated13 and hard to characterize. As indicated by its tree structure, a general r-round LOCC protocol could lead to exponentially many possible results, making LOCC protocol designs for many essential quantum information processing tasks very challenging. At the same time, it will be more practical to consider LOCC protocols with hardware-efficient local operations and a few communication rounds due to the limited coherence time of local quantum memory. To overcome these challenges, we propose to find LOCC protocols with the aid of machine learning, inspired by its recent success in various areas. Specifically, we present the LOCCNet framework, which incorporates optimization methods from classical machine learning field into the workflow of designing LOCC protocols and can simulate any finite round LOCC in principle.
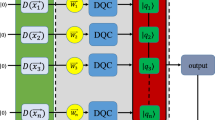
As illustrated in Fig. 1, each party’s local operations, represented by nodes in a tree, are described as parameterized quantum circuits (PQC)23. Users can measure any chosen qubit and define a customized loss function from measurement outcomes as well as remaining states. With a defined loss function for a task of interest, LOCCNet can be optimized to give a protocol. The effect of classical communication is also well simulated by LOCCNet in the sense that different PQCs can be built for different measurement outcomes from previous rounds.
For simplicity, only two parties are involved in this workflow, namely Alice and Bob. The tree presented here corresponds to a specific two-round LOCC protocol. Such a tree can be customized with LOCCNet. With each node (Local Operation) encoded as a PQC and arrows between nodes referring to classical communication, one can define a loss function to guide the training process depending on the task. The tree branch diverges indicating different possible measurement outcomes. Finally, one can adopt optimization methods to iteratively update the parameters in each local operation and hence obtain the optimized LOCC protocol.
Previously, PQCs have been adapted to many research areas including quantum simulation49, quantum optimization1, and quantum error correction50. The family of variational quantum algorithms51,52,53, based on PQCs, is one promising candidate to achieve quantum advantages with near-term devices. In quantum information, PQCs also help in estimating distance measures for quantum states54,55 and compressing quantum data56,57. Here, we take one step further by extending the use of PQCs to the distributed quantum information processing scenario where LOCC is the most natural set of operations.
In the next three sections, we will demonstrate the LOCCNet framework in details with important applications and present some interesting findings, including protocols that achieve better results than existing ones. We conduct software implementations of LOCCNet using the Paddle Quantum toolkit58 on the PaddlePaddle Deep Learning Platform59,60.
Entanglement distillation
Many applications of LOCC involve entanglement manipulation, and the use of entanglement is generally required to be in its pure and maximal form. Hence, the efficient conversion of entanglement into such a form, a process known as entanglement distillation24,42, is usually a must for many quantum technologies. The development of entanglement distillation methods remains at the forefront of quantum information11. For example, the two-qubit maximally entangled state \(\left|{{{\Phi }}}^{+}\right\rangle =1/\sqrt{2}(\left|00\right\rangle +\left|11\right\rangle )\), which is also known as the entangled bit (ebit), is the fundamental resource unit in entanglement theory since it is a key ingredient in many quantum information processing tasks. Thus, an essential goal for entanglement distillation in a two-qubit setting is to convert a number of copies of some two-qubit state ρAB shared by two parties, Alice and Bob, into a state as close as possible to the ebit. Here, closeness between the state ρAB and the ebit is usually measured in terms of the fidelity
Although theory is more concerned with asymptotic distillation with unlimited copies of ρAB, protocols considering a finite number of copies are more practical due to the physical limitations of near-term quantum technologies. Also, practical distillation protocols usually allow for the possibility of failure as a trade-off for achieving a higher final fidelity. Furthermore, due to limited coherence time of local quantum memories, schemes involving only one round of classical communication are preferred in practice. Under these settings, many practical schemes for entanglement distillation have been proposed24,25,61,62,63,64. Not surprisingly, there is not a single scheme that applies to all kinds of states. In fact, designing a protocol even for a specific type of states is a difficult task.
In this section, we apply LOCCNet to entanglement distillation and present selected results that reinforce the validity and practicality of using this framework for designing LOCC protocols. To use LOCCNet for finding distillation protocols for a state ρAB, we build two PQCs, one for Alice and one for Bob. In the preset event of success, these PQCs output a state supposed to have a higher fidelity to the ebit. To optimize PQCs, we define the infidelity of the output state and the ebit, i.e., 1 − F, as the loss function to be minimized. As soon as the value of the loss function converges through training, the PQCs along with the optimized parameters form an LOCC distillation protocol. In principle, this training procedure is general and can be applied to find distillation protocols for any initial state ρAB given its numerical form. Beyond rediscovering existing protocols, we are also able to find improved protocols with LOCCNet. Below, we give two distillation protocols for S states and isotropic states, respectively, as examples of optimized schemes found with LOCCNet.
An S state is a mixture of the ebit \(\left|{{{\Phi }}}^{+}\right\rangle\) and non-orthogonal product noise63. Here, we define it to be
where p ∈ [0, 1]. A distillation protocol known to perform well on two copies of some S state is the DEJMPS protocol25, which in this case outputs a state whose fidelity to the ebit is (1 + p)2/(2 + 2p2) with a probability of (1 + p2)/2 [see Supplementary Note 2].
Here, we present a protocol learned by LOCCNet that can output a state achieving a fidelity higher than DEJMPS and close to the highest possible fidelity. Details on this protocol after simplification are given in Fig. 2, where Alice and Bob apply local operations to their own qubits independently and then compare their measurement outcomes through classical communication. The distillation succeeds only when both Alice and Bob get 0 from computational basis measurements.
This simplified circuit represents local operations in a distillation protocol learned by LOCCNet for two copies of an S state, \({\rho }_{{A}_{0}{B}_{0}}\) and \({\rho }_{{A}_{1}{B}_{1}}\). The rotation angles of both Ry gates are \(\theta =\arccos (1-p)+\pi\), which depend on the parameter p of the S states to be distilled.
The final fidelity achieved by this protocol is compared with that achieved by the DEJMPS protocol in Fig. 3. For the aim of benchmarking, the techniques based on positive partial transpose (PPT) were introduced to derive fundamental limits of entanglement distillation63,65,66,67,68,69. The entanglement theory under PPT operations has been extensively studied in the literature (e.g., refs. 70,71,72,73,74,75) and offers valuable limitations of LOCC. Here, the PPT bound obtained with semi-definite programming63 is an upper bound to the fidelity achieved by any LOCC protocol [see Supplementary Note 2].
As shown in the figure, the protocol learned by LOCCNet achieves near-optimal fidelity in the sense that it is close to the PPT bound. Analytically, for two copies of some S state with a parameter p, the post-measurement state in the event of success is \({\sigma }_{AB}=F\left|{{{\Phi }}}^{+}\right\rangle \left\langle {{{\Phi }}}^{+}\right|+(1-F)\left|{{{\Phi }}}^{-}\right\rangle \left\langle {{{\Phi }}}^{-}\right|\), where
is its fidelity to the ebit and \(\left|{{{\Phi }}}^{-}\right\rangle =1/\sqrt{2}(\left|00\right\rangle -\left|11\right\rangle )\). The probability of arriving at this state is psucc = p2 − p3/2 [see Supplementary Note 2]. It is noteworthy that the distilled state is a Bell diagonal state of rank two. For two copies of such a state, the DEJMPS protocol achieves the optimal fidelity63,76. Thus, combining our protocol with the DEJMPS protocol offers an efficient and scalable distillation scheme for more copies of some S state.
Another important family of entangled states is the isotropic state family, defined as
where p ∈ [0, 1] and I is the identity matrix. Distillation protocols for two copies of some isotropic state have been well studied, and the DEJMPS protocol achieves empirically optimal fidelity in this case. Given four copies of some isotropic state with a parameter p, a common way to distill entanglement is to divide them into two groups of two copies and apply the DEJMPS protocol to each group. Conditioned on success, we then apply the DEJMPS protocol again to the two resulting states from the previous round. Since the DEJMPS protocol was originally designed for two-copy distillation, such a generalization is probably unable to fully exploit the resources contained in four copies of the state. Indeed, with the aid of LOCCNet, we find a protocol optimized specifically for four copies of some isotropic state. As illustrated in Fig. 4, Alice and Bob first apply similar local operations with three pairs of qubits being measured and then compare their measurement outcomes through classical communication. If their measurement outcomes for each pair of qubits are identical, the distillation procedure succeeds.
The fidelity achieved by this protocol for different input isotropic states is plotted in Fig. 5, along with that of the generalized DEJMPS protocol. For four copies of some isotropic state with a parameter p, our protocol achieves a final fidelity of
which is slightly higher than the DEJMPS protocol, as shown in Fig. 5. Details are referred to Supplementary Note 2. Another advantage of this optimized protocol is that the output state in the event of success is still an isotropic state, implying the possibility of a generalized distillation protocol for 4n copies of some isotropic state.
We remark that our protocols are optimized with the goal to achieve the highest possible fidelity, so their probabilities of success are not high. For situations where the probability of success is important, one can also design a customized loss function to optimize a protocol according to their metrics.
Distributed quantum state discrimination
Another important application of LOCC is quantum state discrimination (QSD). Distinguishing one physical configuration from another is central to information theory. When messages are encoded into quantum states for information transmission, the processing of this information relies on the distinguishability of quantum states. Hence, QSD has been a central topic in quantum information77,78,79, which investigates how well quantum states can be distinguished and underlies various applications in quantum information processing tasks, including quantum data hiding80 and dimension witness81.
QSD using global quantum operations is well-understood in the sense that the optimal strategy maximizing the success probability can be solved efficiently via semi-definite programming (SDP)82,83,84. However, for an important operational setting called distant lab paradigm or distributed regime, our knowledge of QSD remains limited despite substantial efforts in the past two decades30,31,32,33,34,35,36,37,38,39,40,41. In the distributed regime, multipartite quantum states are distributed to spatially separated labs, and the goal is to distinguish between these states via LOCC.
For two orthogonal pure states shared between multiple parties, it has been shown that they can be distinguished via LOCC alone no matter if these states are entangled or not31. However, it is not easy to design a concrete LOCC protocol for practical implementation on near-term quantum devices. Using LOCCNet, one can optimize and obtain practical LOCC protocols for quantum state discrimination. Furthermore, for non-orthogonal states, limited aspects have been investigated in terms of the feasibility of LOCC discrimination. However, LOCCNet can provide an optimized and practical protocol in this realistic setting.
Here, to explore the power of LOCCNet in state discrimination, we focus on the optimal success probability of discriminating between noiseless and noisy Bell states via LOCC. Consider two Bell states, \(\left|{{{\Phi }}}^{+}\right\rangle\) and \(\left|{{{\Phi }}}^{-}\right\rangle\), and an amplitude damping (AD) channel \({{{\mathcal{A}}}}\) with noise parameter γ such that \({{{\mathcal{A}}}}(\rho )={E}_{0}\rho {E}_{0}^{{\dagger} }+{E}_{1}\rho {E}_{1}^{{\dagger} }\) with \({E}_{0}=\left|0\right\rangle \left\langle 0\right|+\sqrt{1-\gamma }\left|1\right\rangle \left\langle 1\right|\) and \({E}_{1}=\sqrt{\gamma }\left|0\right\rangle \left\langle 1\right|\). If we send \(\left|{{{\Phi }}}^{-}\right\rangle\)’s two qubits, respectively, through this AD channel, then the resulting state is \({{{\mathcal{A}}}}\otimes {{{\mathcal{A}}}}(\left|{{{\Phi }}}^{-}\right\rangle \left\langle {{{\Phi }}}^{-}\right|)\). The goal is now to distinguish between \(\left|{{{\Phi }}}^{+}\right\rangle \,\left\langle {{{\Phi }}}^{+}\right|\) and \({{{\mathcal{A}}}}\otimes {{{\mathcal{A}}}}(\left|{{{\Phi }}}^{-}\right\rangle \,\left\langle {{{\Phi }}}^{-}\right|)\).
Suppose Φ0 and Φ1 are some pair of two-qubit states. To find a protocol discriminating between them, we build an ansatz with measurements on both qubits. As illustrated in Fig. 6, Alice performs a unitary gate on her qubit followed by a measurement, whose outcome determines Bob’s operation on his qubit. Given an ideal discrimination protocol, Bob’s measurement outcome should be 0 if and only if the input state is Φ0 so that he can tell which state the input state is for sure. Based on this observation, we define a loss function
where P(j∣Φk) is the probability of Bob’s measurement outcome being j given the input state being Φk. By minimizing this loss function, we are able to obtain a protocol for distinguishing between states Φ0 and Φ1 with an optimized probability of success. Specifically, for \({{{\Phi }}}_{0}\equiv \left|{{{\Phi }}}^{+}\right\rangle \,\left\langle {{{\Phi }}}^{+}\right|\) and \({{{\Phi }}}_{1}\equiv {{{\mathcal{A}}}}\otimes {{{\mathcal{A}}}}(\left|{{{\Phi }}}^{-}\right\rangle \,\left\langle {{{\Phi }}}^{-}\right|)\), through optimization we find a protocol where Alice’s local unitary operation is U = Ry(π/2) and Bob’s local unitary operation is V = Ry((−1)aθ) where \(\theta =\pi -\arctan ((2-\gamma )/\gamma )\) and a = 0 or 1 is Alice’s measurement outcome. This optimized protocol achieves an average success probability of
as given in Supplementary Note 3.
In Fig. 7, we compare the protocol learned by LOCCNet with the optimal protocol for perfect discrimination between two noiseless and orthogonal Bell states \(\left|{{{\Phi }}}^{+}\right\rangle\) and \(\left|{{{\Phi }}}^{-}\right\rangle\). The PPT bound shown in Fig. 7 is obtained via SDP and serves as an upper bound to the average probability of any LOCC protocol recognizing the input state correctly85, where the input state is either Φ0 or Φ1 with equal chance. While the noiseless protocol is consistently better than random guessing as noise in the AD channel increases, it inevitably suffers from a decrease in its discrimination ability. The gap between its probability of success and the PPT bound steadily widens. On the other hand, the protocol optimized with LOCCNet can achieve a near-optimal probability of success for each noise setting, as shown in the figure.
Quantum channel simulation
One central goal of quantum information is to understand the limitations governing the use of quantum systems to take advantage of quantum physics laws. Quantum channel lies at the heart of this question since it characterizes what we can do with the quantum states physically86,87,88. To fully exploit quantum resources, the ability to manipulate quantum channels under operational settings is important. Particularly, in distributed quantum computing, one fundamental primitive, dubbed quantum channel simulation, is to realize quantum channels from one party to another using entanglement and LOCC protocols. Quantum channel simulation, exploiting entanglement to synthesize a target channel through LOCC protocols42,43,44,45,46,47,48,89, serves as the basis of many problems in quantum information, including quantum communication, quantum metrology90, and quantum key distribution91.
One famous example of quantum channel simulation is quantum teleportation (i.e., simulation of the identity channel). As one of the most important quantum information processing protocols8,92, quantum teleportation exploits the physical resource of entanglement to realize noiseless quantum channels between different parties and it is an important building block for quantum technologies including distributed quantum computing and quantum networks. Similar to quantum teleportation, quantum channel simulation is a general technique to send an unknown quantum state ψ from a sender to a receiver such that the receiver could obtain \({{{{\mathcal{N}}}}}_{A^{\prime} \to B}({\psi }_{A^{\prime} })\) with the help of a pre-shared entangled state ρAB and an LOCC protocol Π. The overall scheme simulates the target channel \({{{\mathcal{N}}}}\) in the sense that
For some classes of channels such as Pauli channels, the LOCC-based simulation protocols were known42,45,93. However, the LOCC protocols for general quantum channel simulation are hard to design due to the complexity of LOCC. Even for the qubit amplitude damping (AD) channel, the LOCC protocol for simulating this channel in the non-asymptotic regime is still unknown, and its solution would provide a better estimate of its secret key capacity91. Note that the asymptotic simulation of this channel involving infinite dimensions was introduced in ref. 45.
Here, we apply our LOCCNet to explore the simulation of an AD channel \({{{\mathcal{A}}}}\) using its Choi state94\({\rho }_{{{{\mathcal{A}}}}}=(I\otimes {{{\mathcal{A}}}})({{{\Phi }}}^{+})\) as the pre-shared entangled state. Note AD channel is one of the realistic sources of noise in superconducting quantum processor95.
To train the LOCCNet for simulating \({{{\mathcal{A}}}}\), we select a set of linearly independent density matrices S as the training set. The loss function for this channel simulation task is then defined as
where \({{{\mathcal{B}}}}\) is the actual channel simulated by LOCCNet with current parameters and \(F(\rho ,\sigma )=\,{{\mbox{Tr}}}\,{\left(\sqrt{{\rho }^{1/2}\sigma {\rho }^{1/2}}\right)}^{2}\) gives the fidelity between states ρ and σ. With this loss function to be minimized, the parameters in LOCCNet are optimized to maximize the state fidelity between \({{{\mathcal{A}}}}(\psi )\) and \({{{\mathcal{B}}}}(\psi )\) for all ψ ∈ S.
Once the LOCCNet is trained to teleport all the basis states in S with near perfect fidelity, we obtain a protocol for simulating \({{{\mathcal{A}}}}\). For benchmarking, we randomly generate 1000 pure states and teleport them to Bob. The results are summarized in Fig. 8. Compared with the original teleportation protocol, we could achieve an equivalent performance at low noise level and a better performance at noise level γ > 0.4. Note that the numerical simulations are conducted on Paddle Quantum58.
Discussion
We established LOCCNet for exploring LOCC protocols in distributed quantum information processing. Its overall pipeline is standard for machine learning algorithms. For a specific task, one firstly designs an appropriate loss function and then utilizes different LOCCNet structures and optimization methods to train the model to obtain an optimal or near-optimal protocol. Depending on the nature of the task, a selected training data set may be required, as in the case of channel simulation. Based on the current design of LOCCNet, more machine learning techniques, such as reinforcement learning could be incorporated into this framework, making it a more powerful tool for exploring LOCC protocols.
LOCCNet not only unifies and extends the existing LOCC protocols, but also sheds light on the power and limitation of LOCC in the noisy intermediate-scale quantum (NISQ) era12 by providing a plethora of examples. We developed improved protocols for entanglement distillation, local state discrimination, and quantum channel simulation as applications. As a showcase, we applied LOCCNet to establish hardware-efficient and state-of-the-art protocols for entanglement distillation of noisy entangled states of interest. In addition to making a significant contribution to entanglement distillation, LOCCNet finds direct practical use in many settings, as we exemplified with several explicit applications in distinguishing noisy and noiseless Bell states as well as simulating amplitude damping channels.
As we have shown the ability of LOCCNet in discovering improved LOCC protocols, one future direction is to apply LOCCNet to further enhance practical entanglement manipulation and quantum communication and explore fundamental problems in quantum information theory. While in this paper we mainly focus on bipartite cases, LOCCNet also supports multipartite entanglement manipulation. For example, as an essential part in quantum repeaters96, entanglement swapping aims to transform two entangled pairs shared between Alice and Bob and between Bob and Carol into a new entangled pair shared by Alice and Carol using only LOCC. Indeed, we could use LOCCNet to design such a protocol. For instance, we can build an LOCCNet where Bob first operates on and measures his subsystem, and then Alice and Carol perform local operations according to the measurement results from Bob. The loss function to minimize can be defined as the infidelity of a target state and the output state shared between Alice and Carol. Similar procedures can be followed to apply LOCCNet in optimizing other multipartite protocols as well, which is worth exploring in future works.
Another important direction is to extend the framework to the continuous-variable quantum information processing, which may be applied to explore better LOCC protocols of private communication based on continuous variable systems91. As we have seen the potential of advancing distributed quantum information processing with the aid of machine learning, we expect more of such cases with classical machine learning being used to improve quantum technologies, which in turn will enhance quantum machine learning applications.
Data availability
Data that support the plots and other findings of this study are available from the corresponding authors upon reasonable request.
Code availability
Code used in the numerical experiments on quantum channel simulation is available at https://github.com/vsastray/LOCCNetcodes. Other code used in this study is available from the corresponding authors upon reasonable request.
References
Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at http://arxiv.org/abs/1411.4028 (2014).
Harrigan, M. P. et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 17, 332–336 (2021).
McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. & Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 92, 015003 (2020).
Arute, F. et al. Hartree-Fock on a superconducting qubit quantum computer. Science 369, 1084–1089 (2020).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In International Conference on Computers, Systems & Signal Processing, Bangalore, India, Dec 9-12, 1984, 175–179 (1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195–202 (2017).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Bennett, C. H. & Wiesner, S. J. Communication via one-and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 69, 2881 (1992).
Plenio, M. B. & Virmani, S. S. An introduction to entanglement measures. Quantum Inf. Comput. 7, 1–51 (2007).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Chitambar, E., Leung, D., Mančinska, L., Ozols, M. & Winter, A. Everything you always wanted to know about LOCC (but were afraid to ask). Commun. Math. Phys. 328, 303–326 (2014).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).
Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).
Mavadia, S., Frey, V., Sastrawan, J., Dona, S. & Biercuk, M. J. Prediction and real-time compensation of qubit decoherence via machine learning. Nat. Commun. 8, 14106 (2017).
Wan, K. H., Dahlsten, O., Kristjánsson, H., Gardner, R. & Kim, M. S. Quantum generalisation of feedforward neural networks. npj Quantum Inf. 3, 36 (2017).
Lu, D. et al. Enhancing quantum control by bootstrapping a quantum processor of 12 qubits. npj Quantum Inf. 3, 1–7 (2017).
Niu, M. Y., Boixo, S., Smelyanskiy, V. N. & Neven, H. Universal quantum control through deep reinforcement learning. npj Quantum Inf. 5, 33 (2019).
Wallnöfer, J., Melnikov, A. A., Dür, W. & Briegel, H. J. Machine learning for long-distance quantum communication. PRX Quantum 1, 010301 (2020).
Bausch, J. & Leditzky, F. Quantum codes from neural networks. New J. Phys. 22, 023005 (2020).
Benedetti, M., Lloyd, E., Sack, S. & Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 4, 043001 (2019).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Deutsch, D. et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77, 2818 (1996).
Murao, M., Plenio, M. B., Popescu, S., Vedral, V. & Knight, P. L. Multiparticle entanglement purification protocols. Phys. Rev. A 57, R4075–R4078 (1998).
Dür, W. & Briegel, H. J. Entanglement purification and quantum error correction. Rep. Prog. Phys. 70, 1381–1424 (2007).
Pan, J.-W., Gasparoni, S., Ursin, R., Weihs, G. & Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 423, 417–422 (2003).
Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A. 461, 207–235 (2005).
Bennett, C. H. et al. Quantum nonlocality without entanglement. Phys. Rev. A 59, 1070–1091 (1999).
Walgate, J., Short, A. J., Hardy, L. & Vedral, V. Local distinguishability of multipartite orthogonal quantum states. Phys. Rev. Lett. 85, 4972 (2000).
Fan, H. Distinguishability and indistinguishability by local operations and classical communication. Phys. Rev. Lett. 92, 177905 (2004).
Hayashi, M., Markham, D., Murao, M., Owari, M. & Virmani, S. Bounds on multipartite entangled orthogonal state discrimination using local operations and classical communication. Phys. Rev. Lett. 96, 40501 (2006).
Ghosh, S., Kar, G., Roy, A. & Sarkar, D. Distinguishability of maximally entangled states. Phys. Rev. A 70, 22304 (2004).
Nathanson, M. Distinguishing bipartitite orthogonal states using LOCC: best and worst cases. J. Math. Phys. 46, 062103 (2005).
Duan, R., Feng, Y., Ji, Z. & Ying, M. Distinguishing arbitrary multipartite basis unambiguously using local operations and classical communication. Phys. Rev. Lett. 98, 230502 (2007).
Chitambar, E., Duan, R. & Hsieh, M.-H. When do local operations and classical communication suffice for two-qubit state discrimination? IEEE Trans. Inf. Theory 60, 1549–1561 (2014).
Duan, R., Feng, Y., Xin, Y. & Ying, M. Distinguishability of quantum states by separable operations. IEEE Trans. Inf. Theory 55, 1320–1330 (2009).
Childs, A. M., Leung, D., Mančinska, L. & Ozols, M. A framework for bounding nonlocality of state discrimination. Commun. Math. Phys. 323, 1121–1153 (2013).
Li, Y., Wang, X. & Duan, R. Indistinguishability of bipartite states by positive-partial-transpose operations in the many-copy scenario. Phys. Rev. A 95, 052346 (2017).
Bandyopadhyay, S. et al. Limitations on separable measurements by convex optimization. IEEE Trans. Inf. Theory 61, 3593–3604 (2014).
Bennett, C. H., DiVincenzo, D. P., Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996).
Bennett, C. H., Devetak, I., Harrow, A. W., Shor, P. W. & Winter, A. The quantum reverse Shannon theorem and resource tradeoffs for simulating quantum channels. IEEE Trans. Inf. Theory 60, 2926–2959 (2014).
Berta, M., Brandao, F. G. S. L., Christandl, M. & Wehner, S. Entanglement cost of quantum channels. IEEE Trans. Inf. Theory 59, 6779–6795 (2013).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Wilde, M. M. Entanglement cost and quantum channel simulation. Phys. Rev. A 98, 042338 (2018).
Wang, X. & Wilde, M. M. Exact entanglement cost of quantum states and channels under PPT-preserving operations. Preprint at http://arxiv.org/abs/1809.09592 (2018).
Fang, K., Wang, X., Tomamichel, M. & Berta, M. Quantum channel simulation and the channel’s smooth max-information. IEEE Trans. Inf. Theory 66, 2129–2140 (2020).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
Johnson, P. D., Romero, J., Olson, J., Cao, Y. & Aspuru-Guzik, A. QVECTOR: an algorithm for device-tailored quantum error correction. Preprint at http://arxiv.org/abs/1711.02249 (2017).
Cerezo, M. et al. Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644 (2021).
Bharti, K. et al. Noisy intermediate-scale quantum (NISQ) algorithms. Preprint at http://arxiv.org/abs/2101.08448 (2021).
Endo, S., Cai, Z., Benjamin, S. C. & Yuan, X. Hybrid quantum-classical algorithms and quantum error mitigation. J. Phys. Soc. Jpn. 90, 032001 (2021).
Chen, R., Song, Z., Zhao, X. & Wang, X. Variational Quantum Algorithms for Trace Distance and Fidelity Estimation. Preprint at http://arxiv.org/abs/2012.05768 (2020).
Cerezo, M., Poremba, A., Cincio, L. & Coles, P. J. Variational quantum fidelity estimation. Quantum 4, 248 (2020).
Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. Quantum Sci. Technol. 2, 045001 (2017).
Cao, C. & Wang, X. Noise-assisted quantum autoencoder. Phys. Rev. Applied 15, 054012 (2021).
Paddle Quantum. https://github.com/PaddlePaddle/Quantum (2020).
Ma, Y., Yu, D., Wu, T. & Wang, H. PaddlePaddle: an open-source deep learning platform from industrial practice. Front. Data Comput. 1, 105–115 (2019).
PArallel Distributed Deep LEarning: Machine learning framework from industrial practice. https://github.com/paddlepaddle/paddle (2016).
Fujii, K. & Yamamoto, K. Entanglement purification with double selection. Phys. Rev. A 80, 042308 (2009).
Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
Rozpedek, F. et al. Optimizing practical entanglement distillation. Phys. Rev. A 97, 062333 (2018).
Krastanov, S., Albert, V. V. & Jiang, L. Optimized entanglement purification. Quantum 3, 123 (2019).
Rains, E. M. A semidefinite program for distillable entanglement. IEEE Trans. Inf. Theory 47, 2921–2933 (2000).
Matthews, W. & Winter, A. Pure-state transformations and catalysis under operations that completely preserve positivity of partial transpose. Phys. Rev. A 78, 012317 (2008).
Wang, X. & Duan, R. Improved semidefinite programming upper bound on distillable entanglement. Phys. Rev. A 94, 050301 (2016).
Fang, K., Wang, X., Tomamichel, M. & Duan, R. Non-asymptotic entanglement distillation. IEEE Trans. Inf. Theory 65, 6454–6465 (2019).
Wang, X. & Duan, R. Nonadditivity of Rains’ bound for distillable entanglement. Phys. Rev. A 95, 062322 (2017).
Audenaert, K., Plenio, M. B. & Eisert, J. Entanglement cost under positive-partial-transpose-preserving operations. Phys. Rev. Lett. 90, 027901 (2003).
Wang, X. & Duan, R. Irreversibility of asymptotic entanglement manipulation under quantum operations completely preserving positivity of partial transpose. Phys. Rev. Lett. 119, 180506 (2017).
Regula, B., Fang, K., Wang, X. & Gu, M. One-shot entanglement distillation beyond local operations and classical communication. New J. Phys. 21, 103017 (2019).
Chitambar, E., de Vicente, J. I., Girard, M. W. & Gour, G. Entanglement manipulation beyond local operations and classical communication. J. Math. Phys. 61, 042201 (2020).
Wang, X., Fang, K. & Duan, R. Semidefinite programming converse bounds for quantum communication. IEEE Trans. Inf. Theory 65, 2583–2592 (2019).
Wang, X. & Wilde, M. M. Cost of quantum entanglement simplified. Phys. Rev. Lett. 125, 040502 (2020).
Ruan, L., Dai, W. & Win, M. Z. Adaptive recurrence quantum entanglement distillation for two-Kraus-operator channels. Phys. Rev. A 97, 052332 (2018).
Bae, J. & Kwek, L.-C. Quantum state discrimination and its applications. J. Phys. A 48, 083001 (2015).
Barnett, S. M. & Croke, S. Quantum state discrimination. Adv. Opt. Photon. 1, 238–278 (2009).
Li, K. Discriminating quantum states: the multiple Chernoff distance. Ann. Statist. 44, 1661–1679 (2016).
DiVincenzo, D. P., Leung, D. W. & Terhal, B. M. Quantum data hiding. IEEE Trans. Inf. Theory 48, 580–598 (2002).
Gallego, R., Brunner, N., Hadley, C. & Acín, A. Device-independent tests of classical and quantum dimensions. Phys. Rev. Lett. 105, 230501 (2010).
Eldar, Y. A semidefinite programming approach to optimal unambiguous discrimination of quantum states. IEEE Trans. Inf. Theory 49, 446–456 (2003).
Sun, X., Zhang, S., Feng, Y. & Ying, M. Mathematical nature of and a family of lower bounds for the success probability of unambiguous discrimination. Phys. Rev. A 65, 44306 (2002).
Ježek, M., Reháček, J. & Fiurášek, J. Finding optimal strategies for minimum-error quantum-state discrimination. Phys. Rev. A 65, 60301 (2002).
Yu, N., Duan, R. & Ying, M. Distinguishability of quantum states by positive operator-valued measures with positive partial transpose. IEEE Trans. Inf. Theory 60, 2069–2079 (2014).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge Univ. Press, 2010).
Wilde, M. M. Quantum Information Theory (Cambridge Univ. Press, 2017).
Watrous, J. The Theory of Quantum Information (Cambridge Univ. Press, 2018).
Pirandola, S. et al. Theory of channel simulation and bounds for private communication. Quantum Sci. Technol. 3, 035009 (2018).
Pirandola, S. & Lupo, C. Ultimate precision of adaptive noise estimation. Phys. Rev. Lett. 118, 100502 (2017).
Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt. Photon. 12, 1012 (2020).
Pirandola, S., Eisert, J., Weedbrook, C., Furusawa, A. & Braunstein, S. L. Advances in quantum teleportation. Nat. Photonics 9, 641–652 (2015).
Horodecki, M., Horodecki, P. & Horodecki, R. General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 60, 1888–1898 (1999).
Choi, M.-D. Completely positive linear maps on complex matrices. Linear Algebra Appl. 10, 285–290 (1975).
Chirolli, L. & Burkard, G. Decoherence in solid-state qubits. Adv. Phys. 57, 225–285 (2008).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Acknowledgements
We would like to thank Runyao Duan and Kun Fang for helpful discussions.
Author information
Authors and Affiliations
Contributions
X.W. formulated the initial idea and the framework; X.Z. and B.Z. developed the theory; X.Z., B.Z., Z.W. and Z.S. performed the experiments. All co-authors contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, X., Zhao, B., Wang, Z. et al. Practical distributed quantum information processing with LOCCNet. npj Quantum Inf 7, 159 (2021). https://doi.org/10.1038/s41534-021-00496-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00496-x
This article is cited by
-
Quantum self-attention neural networks for text classification
Science China Information Sciences (2024)
-
Enhancing quantum teleportation: an enable-based protocol exploiting distributed quantum gates
Optical and Quantum Electronics (2023)
-
Quantum NETwork: from theory to practice
Science China Information Sciences (2023)
-
Detecting and quantifying entanglement on near-term quantum devices
npj Quantum Information (2022)