Quantum Fourier transform for nanoscale quantum sensing

Abstract

The quantum Fourier transformation (QFT) is a key building block for a whole wealth of quantum algorithms. Despite its proven efficiency, only a few proof-of-principle demonstrations have been reported. Here we utilize QFT to enhance the performance of a quantum sensor. We implement the QFT algorithm in a hybrid quantum register consisting of a nitrogen-vacancy (NV) center electron spin and three nuclear spins. The QFT runs on the nuclear spins and serves to process the sensor—i.e., the NV electron spin signal. Specifically, we show the application of QFT for correlation spectroscopy, where the long correlation time benefits the use of the QFT in gaining maximum precision and dynamic range at the same time. We further point out the ability for demultiplexing the nuclear magnetic resonance (NMR) signals using QFT and demonstrate precision scaling with the number of used qubits. Our results mark the application of a complex quantum algorithm in sensing which is of particular interest for high dynamic range quantum sensing and nanoscale NMR spectroscopy experiments.

Introduction

Diamond spin-based quantum sensing has advanced nanoscale sensing and in particular nuclear magnetic resonance (NMR) studies to a level where signals from zeptoliters sample volumes can be detected. Initially the spectral resolution was too low to achieve chemical specificity, a hallmark of standard NMR. Meanwhile, however, classical and quantum protocols have achieved better than Hz spectral resolution. An additional remaining challenge is, that NMR spectra usually comprise a whole wealth of spectral components. In conventional NMR the technique most widely used to attain the required spectral resolution and simultaneously efficiently measure whole spectra is Fourier transform spectroscopy. In this method the temporal evolution of the spin system is measured and a subsequent Fourier transform yields the NMR spectrum. The question at hand is, if there is a similar quantum sensing strategy in nanoscale NMR.

In quantum sensing one usually measures the periodic phase evolution of a quantum system in response to an external quantity. The periodic evolution of the spin sensor is followed as long as possible to gain maximum sensitivity. However, as the NMR signals contain multiple frequencies, which needs to be resolved, the challenge at hand is not only one of maximum interaction time but also of the sensors dynamic range. Here we show, that applying the quantum Fourier transformation is instrumental to enlarge the sensors dynamic range while at the same time allowing for large interaction times, i.e., high sensitivity. We apply this method to measuring the NMR signal of single nuclei by using a single nitrogen-vacancy center with nuclear spin ancillary qubits.

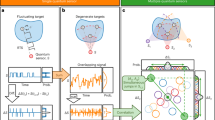
The most widely used method to measure the phase evolution of the sensor is a correlation measurements. The scheme consists of two phase acquisition steps which are separated by a long correlation time T_c (see Fig. 1b). Essentially rather than measuring the phase once, it is measured twice and the relative phase evolution over the time T_c determines the signal strength to be measured. To achieve the best possible sensitivity in each of the two phase acquisition steps interrogation times τ close to the decoherence limit T₂ of the sensor are used, which results in acquiring a maximum phase ϕ. On the other hand, such choice of τ could result in ϕ more than π and thereby in an ambiguity in determining the actual strength of the signal. This becomes ultimately important when dealing with a high dynamic range correlation signal with multiple frequency components of various strengths. In the case of a nanoscale NMR signal, which is composed of multiple frequencies f_i and amplitudes a_i this results in a beating of the free precession signal requiring a high dynamic range sensing method (see Fig. 1b). Thus, the problem at hand is to design a phase correlation measurement protocol that at the same time yields a large dynamic range and allows for high spectral resolution (i.e., long correlation times T_c).

Fig. 1: Quantum Fourier transform for correlation measurements with quantum sensor–register system.

a Schematic representation of the sensor consisting of a single sensor spin (green) which collects phase information of a distant target spin (blue and orange) and distributes it onto a local qubit register (red) made of one qutrit (¹⁴N nuclear spin) and two qubits (¹³C nuclear spins). b The target system spectrum, consisting of multiple frequencies f₁, f₂,... with corresponding amplitudes a₁, a₂,... with a schematic circuit for sensing of multiple target spins with implementation of QFT and QFT^†. c The phase acquisition unitary gate for sensing of target nuclear spins t₁ and t₂. d The readout result of the register qubits after performing measurements with the QFT algorithm. Each memory stores Ramsey oscillation of individual target nuclear spins. e QFT^† quantum circuit for our hybrid quantum register.

This known dynamic range - sensitivity¹ trade-off could be tackled by a family of phase estimation algorithms, including Bayessian, adaptive and machine learning sensing protocols^{1,2,3,4,5,6,7,8} and the ones based on inverse quantum Fourier transform (QFT)^9,10,11. As correlation measurements typically have a large time overhead (T_c = 10–20 ms) in comparison to the sensing times (τ = 10–100 μs)¹² (also see SI for times used in present manuscript), repetitive measurements within each correlation step required in the adaptive techniques may not be well suitable. Further, including the influence of the quantum back-action in such repetitive measurements leads to erroneous results on the measured dynamics^13,14. On the other hand, phase estimation using the inverse QFT could resolve ambiguities in each run (measurement) of the protocol and provide a sensitivity that is only limited by the coherence time of the sensor. In this work, we advance the correlation measurement protocol with phase estimation based on the inverse QFT algorithm using the NV center and a three nuclear spin register. We utilize the QFT^† and QFT as a convenient transformation to convert the acquired phase to the population basis of the register. To demonstrate and benchmark the scope of QFT-based phase estimation we perform here three different experiments using both classical and quantum fields. We first start by demonstrating the phase to population mapping by QFT and show how it differs from the standard Ramsey measurements which do the same. After this we benchmark the QFT^† algorithm and perform high dynamic range sensing of an artificial classical AC-signal generated by the RF source. Later we extend it to the correlation spectroscopy protocol of the nuclear spin-bath and demonstrate the demultiplexing of target spin-signals onto separate register qubits outputs. As the sensor readout performed only at the end of the protocol, an entanglement generated prior to the readout could be preserved and the studied quantum signal is correlated in-situ. Finally, we investigate the scaling behavior when using our protocol with a larger number of qubits in the register. We show that one can achieve improvement in signal-to-noise level in correlation measurements with larger number of bits similar to classical analog to digital conversion (ADC).

Results

Experimental platform

As a sensor, we use the electron spin of the NV center in diamond. As a memory register, we use three well isolated and thus long-lived individual nearby nuclear spins (¹⁴N with I = 1, ¹³C₁, ¹³C₂ with I = 1/2) which form a twelve-level quantum system (Fig. 1a). The electron spin has a long coherence time T₂ = 430 μs at room temperature and is sensitive to various fields in the environment^15,16,17. Its susceptibility to magnetic fields is used for the acquisition of a phase during the interrogation time τ. Entanglement of the quantum memory and the quantum sensor during the interrogation time allows us to directly encode the phase into the memory state. The three nuclear spins are probed with single-shot readout highlighted previously^18,19,20,21. We develop a metrological high dynamic range correlation protocol that is adapted to our hybrid qubit-qutrit quantum register-sensor system (see Fig. 1c). As in previous work on correlation spectroscopy^12,22, it consists of two interrogation steps separated by a long correlation time T_c. However, in contrast to the paper by Zaiser et al., QFT and QFT^† are used as a generalization of the Hadamard (H) gate in each interrogation.

The sensor is initialized in the $\left|0\right\rangle$ state. The register spins are initialized in a superposition state with zero relative phases using local Hadamard and Chrestenson²³ (see SI section II.C) gates applied to the register prepared in the $\left|000\right\rangle$ state which results in a net state ${\left|0\right\rangle }_{e}\otimes (\left|0\right\rangle +\left|1\right\rangle )\otimes (\left|0\right\rangle +\left|1\right\rangle )\otimes (\left|0\right\rangle +\left|1\right\rangle +\left|2\right\rangle )/\sqrt{12}$. A C_kNOT_e gate, where k labels the nuclear spin (k = 0, 1, 2), results in entangled state of electron spin and k-th nuclear spin, e.g., $({\left|0\right\rangle }_{e}\left|0\right\rangle +{\left|1\right\rangle }_{e}\left|1\right\rangle )\otimes (\left|0\right\rangle +\left|1\right\rangle )\otimes (\left|0\right\rangle +\left|1\right\rangle +\left|2\right\rangle )/\sqrt{12}$ for k = 0 and via the interaction between the target system and electron spin attains a phase ϕ₁ during the interrogation time τ The interaction process can be described with a unitary operator of the form ${U}^{r}=\exp \{ir{\hat{H}}_{I}\tau \}$ where r = 2^k, ${\hat{H}}_{I}$ is the sensor-target system effective Hamiltonian during the application of the control sequence (see Fig. 1b, c). After attaining the phase, the state of memory is disentangled from electron spin with another C_kNOT_e gate and leaves the state in ${\left|0\right\rangle }_{e}\otimes (\left|0\right\rangle +{e}^{i{\phi }_{1}}\left|1\right\rangle )\otimes (\left|0\right\rangle +{e}^{i2{\phi }_{1}}\left|1\right\rangle )\otimes (\left|0\right\rangle +{e}^{i4{\phi }_{1}}\left|1\right\rangle +{e}^{i8{\phi }_{1}}\left|2\right\rangle )/\sqrt{12}={\left|0\right\rangle }_{e}\otimes \left|{\phi }_{1}\right\rangle \otimes \left|2{\phi }_{1}\right\rangle \otimes \left|4{\phi }_{1},8{\phi }_{1}\right\rangle$ (see SI IV.D and ref. ²² for details).

QFT^† maps the attained phase state of the register $\left|{{{\Psi }}}_{1}\right\rangle =\left|{\phi }_{1}\right\rangle \otimes \left|2{\phi }_{1}\right\rangle \otimes \left|4{\phi }_{1},8{\phi }_{1}\right\rangle$ to a bit representation which is then used as a classical memory during the correlation time T_c which could be longer than the coherence time of the register (≈5 ms). After that, the QFT algorithm retrieves the $\left|{{{\Psi }}}_{1}\right\rangle$ state with 0.7 purity after possible decoherence (see SI Fig. 5 for details). The second measurement step similarly gains a phase ϕ₂. By inverting the condition in the CNOT gates this results in a state with net phase Δϕ = ϕ₁ − ϕ₂ encoded in the nuclear spin register, similar to²². Finally, QFT^† brings the state with phase difference Δϕ into the I_z basis for readout.

Realization of the QFT

 Fig. 1e shows a circuit representation of a QFT and QFT^† algorithm for an effective twelve-level system, consisting of one qutrit and two qubits (see SI. S.II). In general, the QFT involves local Hadamard (Chrestenson) gates for qubits (qutrit) and a large number $(O({n}_{q}^{2}))$ of conditional non-local rotational gates, which are implemented using optimal control to enhance fidelity. The addition of a qutrit system extends the available Hilbert space dimension. However, the implementation of QFT for hybrid system involves additional gates, generalized qutrit-controlled rotational gates and generalized local Chrestenson gates, for derivation of arbitrary hybrid qudit register QFT circuit see SI S.II

In our protocol, the role of the QFT^† is to map the attained phases efficiently and unambiguously. To demonstrate this we prepare the initial state of the register with the phase ϕ which mimics a phase acquired by the sensor spin (see Fig. 2) (see SI S.IV.J). The figure shows the result of a readout of the nuclear spin register (i.e., its bit values) for different input. The simplest way to convert the phase of the nuclear spin quantum states into a detectable 〈I_z〉 is to apply the Hadamard gates on each nuclear spin. For comparison, we show the result of the same initial state with conversion to the computational basis via the QFT^† protocol. In Fig. 2b, c the analytical and experimental result for the application of H^⊗2 ⊗ C and QFT^† on the same initial phase-encoded state is shown respectively. As apparent from the upper row of Fig. 2b, c the application of Hadamard gates results in quantum register readouts scattered throughout the whole logical space, which prevents unambiguous estimation of the phase ϕ. In contrast to local Hadamard gates a linear mapping is maintained upon the application of QFT^†, and the measurement output corresponds to a well-defined phase. This allows to estimate the phase of the register in few measurements of the register as it localizes its probability distribution within a narrow interval given by $\delta \phi \approx 1/({2}^{{n}_{q}}-1)$²⁴. In addition, the QFT-based protocol maps the individual qubits onto their eigenstates during T_c. The advantage is, that in the case of local H^⊗n gates T_c is limited by T₂ while for the QFT-based protocol the T_c is limited by T₁ being much longer than T₂. This could be explained, as during the T₂ decay of the memory register, the purity of the register state decays with number of qubits involve, while for QFT^† based algorithm, it stays constant at ≈0.7 (see SI S. IV.l). We note that in the absence of quantum back-action the case of the H-based protocol could be further improved by introducing semiclassical and measurement-based schemes^8,10,24.

Fig. 2: Measurement outcome of the register after two readout methods and demonstration of high dynamic range AC field detection with QFT^†.

a Quantum circuits of readout methods of register prepared in arbitrary phase state $\left|{{\Psi }}\right\rangle =\left|\phi \right\rangle \otimes \left|2\phi \right\rangle \otimes \left|4\phi ,8\phi \right\rangle$ using local single qubit (qutrit) Hadamard gates. Results of calculations and experimental realization of the circuits on our system. b Same using QFT^† algorithm. Notably in the QFT^† case there is no ambiguity between regions of phase 0 − π and π − 2π. Additionally the QFT^† prepares final states which are close to the eigen states of the register, minimizing the loss of purity due to dephasing. c Schematic representation of the quantum circuit which serves for detection of the artificial field. d Realisation of XY-N detection scheme for AC field sensing. e Measurement outcome of the memory registers.

Detection of artificial AC magnetic field with QFT

We directly apply the QFT^† to quantum phase estimation protocol to demonstrate high dynamic range sensing of AC fields with our full 12 level quantum register. For this, we perform the measurements, where instead of preparing the register in a particular state ϕ we acquire a phase via sensing of an external RF field (see Fig. 2c, d). We design and implement phase gates ${\hat{ U}}^{{2}^{k}}=\exp \{i{2}^{k}{N}_{p}\tau {B}_{ac}\ {\hat{S}}_{z}\}$ which convert the AC magnetic field into a phase acquired by the electron spin of the NV center and imprint it onto the various nuclear qubit registers. ${\hat{U}}^{{2}^{k}}$ comprises a train of N_p phase inversion pulses which are commensurate with the oscillation of the AC magnetic field B_ac sandwiched between two c_kNOT_e gates which entangle the sensor with the memory and thus imprint the phase ϕ on the nuclear register (see Fig. 2c, d). The phase is digitized through the QFT^† into a binary representation, which is then finally readout. Fig. 2e shows the output of the QFT^† in the register states basis representation $\left|{m}_{1}{m}_{2}{m}_{3}\right\rangle$. Analogous to Fig. 2a, b, the image shows the unambiguous representation of the field amplitude with respect to the measurement result output, which corresponds to the full $2\pi * (1-1/{2}^{{n}_{q}})$ phase estimation range on the twelve-level quantum register. With our method the achieved estimated sensitivity is $24\ {{{{{\rm{nT}}}}}}/\sqrt{{{{{{\rm{Hz}}}}}}}$ and maximum unambiguously resolved field B_ac = 2.2 μT, which results in dynamic range $DR\approx 84\sqrt{{{{\rm{Hz}}}}}$. In comparison to single qubit Ramsey-like scheme performed with same system (e.g., see Supplementary IV.F) the dynamic range is improved by 4.2 which is in agreement with 1/T scaling¹. In contrast to previous realization of high dynamic range sensing protocols involving adaptive⁴, non-adaptive⁵, and machine learning⁶, our approach is realized in fully quantum single-shot way, and demonstrates expected dynamic range performance.

Application of the developed correlation protocol in nanoscale NMR spectroscopy

We now apply our protocol to measure the correlation signal of multiple, non-identical nuclear spins close to the NV center via in-situ correlation spectroscopy^12,22,25, which is developed for chemically resolved NMR spectra at nanoscale with single quantum sensors such as NV center electron spin. In this work we extend existing protocols with a two qubit memory and make use of the QFT and inverse QFT to convert the register between phase and population basis. The general working principle of this method is depicted schematically in Fig. 3a. The target nuclei are probed and the result of the interaction is encoded into the register state in the phase basis followed by conversion to the I_z basis using the inverse QFT, similar to the above detection of the test field. The phase acquisition sequence is repeated after a correlation time T_c and QFT as mentioned above. During the correlation interval T_c the target spins undergo free evolution. In case of target spins not evolving the protocol would result in a net relative zero phase. We perform correlation spectroscopy of two target spins with A_zz,1 = 6 kHz and A_zz,2 = 12.4 kHz. During the correlation time T_c we perform a Ramsey sequence on the two target spins. For the nuclear spin Ramsey RF pulses, a frequency detuning of 2.5 kHz to the weaker coupled target spin was chosen, to generate an oscillation in their signal with approximately 2.5 kHz and 3.9 kHz, respectively. To achieve an efficient detection of the nuclear spin signals, we adjust the phase acquisition such that the least significant qubit (LSQ) acquires a total phase ϕ_LSQ = 4 ⋅ 2τA_zz,2 = 2π and the most significant qubit (MSQ) a phase of ϕ_MSQ = 4 ⋅ τA_zz,2 = π as the stronger coupled target t₂ spin flips during the correlation time T_c. ϕ_LSQ = 4 ⋅ 2τA_zz,1 = π on the LSQ and ${\phi }_{MSQ}=4\cdot \tau {A}_{zz,1}=0\ ({{{{{\rm{mod}}}}}}\ 2\pi )$ on the MSQ when the weaker coupled target spin t₁ flips. Hence, we pick a sensing time τ, such that it fits the energy difference of the combined target spins. In our case, the sensing time τ was chosen to be τ = 3π/8 ⋅ (A_zz,1 + A_zz,2) ≈ (4⋅ 12 kHz)⁻¹ as depicted in Fig. 3c, d. As a result when performing Ramsey-type correlation measurement on two target spins their oscillation are directly mapped onto the output populations of memory spins which are read out in Fig. 3e. By performing the fast-Fourier transform (FFT) on the results of individual memory outputs we show two resonances corresponding to 12 and 6 kHz ¹³C nuclear spins with resolution of ≈70 Hz (≈10 ppm), depicted in Fig. 3f.

Fig. 3: High resolution correlation spectroscopy of target nuclear spins with Quantum Fourier Transform.

a 5-qubit circuit for high resolution spectroscopy. Metrology information is decoded first with a single quantum phase estimation algorithm step and with a filter to preselect the target spins of interest. b Controlled unitaries Uⁿ consist of two CROT gates with different states of the control qubit separated by nτ. The unitary is realized though A_zzI_zS_z interaction. c Representation of the phase acquired by two register qubits. The phase results from two target spin contributions proportional to their coupling strength and conditional on the target spin state. The net amount of phase on the second qubit is twice larger than on the third in order to match the requirement of the QFT transformation. d Acquired phase digitization on register states. First target spin is responsible for the flip of least significant qubit, while second target spin is responsible for the flip of most significant qubit. e Ramsey measurement on two target spins as shown in (a). After performing a FFT on the data (shown in (f)), two distinct peaks arise with a linewidth of a 100 Hz allowing to distinguish between the two target spins.

Scaling with number of qubits

Finally, we discuss the advantages of using QFT and scaling with the number of qubits. The QFT is known to be a time-optimal solution for phase estimation²⁶. Here we estimate how the precision of the signal estimation scales with the number of qubits for time evolving signals, which could originate either from AC signal sensing or nanoscale correlation spectroscopy of nuclear spin bath. In classical signal processing, typically the signal is digitized with an analog-to-digital converter (ADC). This compression procedure inevitably produces digitization noise²⁷ which approximately follows SNR = 6.03N_bits + C, where N_bits is the number of effective bits, C is a constant determined by the signal, and SNR is the signal-to-noise level in decibels. We note, that in this regard, the QFT is analogous to a classical ADC. Though the phase acquisition is deterministic, the readout process is stochastic which leads to the fact that the noise performance is identical to single-bit ADC with tethered output (see Fig. 4d). Analogous to a multi-bit ADC, our multiqubit register has more than two eigenstates onto which it could be projected. This results in a finer digitization of the signal amplitude. Fig. 4a shows a comparison of phase digitization using different numbers of qubits. To understand the scaling with the number of qubits involved we simulate the response of the sensor–register system. We artificially compose a correlation signal composed of random frequency components (see “Methods”) in a spectrally narrow region with random amplitudes. In Fig. 4a the register final eigenstate probability distribution is depicted. For a single qubit this is a binominal Bernoulli stochastic process. To reliably obtain the signal shape multiple trials N_m of the process are necessary (see Fig. 4b). The uncertanity of the normalized signal estimation after N_m trials scales as $\sqrt{p(1-p){N}_{m}}$. With more qubits, the probability distribution of the register eigenstates shows a pattern similar to the incident signal 4a. It is constrained within few highly probable neighboring register output states thus reducing the uncertainty of signal estimation as shown in Fig. 4b. We perform a Monte-Carlo simulation of projective measurements with different number of qubits (see Fig. 4b). We reconstruct the signal value using the register output, similar to reading out an ADC. In our simulation, we apply an identical signal to a classical ADC and our quantum protocol and estimate the difference between the actual and the estimated signal. For a thorough comparison, we consider a classical ADC digitizer with deterministic and tethered output. The results for a classical ADC are in agreement with the approximate scaling law SNR = 6.02N_bits + 1.76 dB²⁷. For the quantum digitizer case, we see a different behavior. Due to the probabilistic nature of quantum measurements, a measurement output with large deviation from the most probable value occurs, which results in a worse scaling compared to a classical ADC. However, we note that the SNR in a register of 4 qubits sampled once is capable of having similar SNR levels as a single qubit register sampled 100 times.

Fig. 4: Multiqubit digitization of an arbitrary signal.

a Simulated probabilities of 1, 3, and 5 qubit digitizer when detecting a high dynamic range signal. b Simulated actual signal derived from the acquired phase (solid line), and average of 100 trials of a 1 qubit sensor output and 3bit classical ADC. c Experimentally and numerically determined Fisher information estimated for the case of the inverse Quantum Fourier Transform (QFT^†) sensing protocol, and the Standard Quantum Limit (SQL). Red dashed line marks a simulation of the QFT^† on the n-qubit circuit. Violet and green romb points are experimental results of the bare QFT^† algorithm and the QFT^† with sensing steps from data depicted in Fig. 2. n_q = 3.5 is used to express 2 qubits and 1 qutrit, resulting in 12 level quantum register. d The signal-to-noise of the sensor output as a function of (quantum) bits. Solid violet curve is deterministic classical ADC. The dashed lines represent the canonical SNR = 6.03 N_bits + C (db) of the classical ADC with noise and single (blue) and 16 trials of signal sampling. Solid read and green curves are quantum sensor with QPEA. Red - single trial of signal sampling, green—100 trials.

To further see the benefit of using a QFT-based quantum phase estimation, we analyze the Fisher information in Fig. 4d. To this end, we analyze the output state in the sensing protocol as a function of the acquired phase ϕ, using the expression for the quantum Fisher information for pure states, F_q = 4(〈∂_ϕψ∣∂_ϕψ〉 − ∣〈∂_ϕψ∣ψ〉∣²). We estimate the theoretical Fisher information of the final state of the sensing protocol with respect to the parameter Δϕ, and compare it to the expressions obtained for the case of n non-entangled qubits, which represents the Standard Quantum limit in a number of used qubit resources (see SI S.I). In the same plot, we show the experimentally achieved values of the Fisher information for the case of a twelve-level register which we denote as n_q = 3.5. These values were estimated from the experiment shown in Fig. 2 for the bare QFT^† (Fig. 2b) and QFT^† with sensing (Fig. 2e). While the experimental values show a slight deviation in the achievable information compared to the theoretically calculated case, they outperform the Standard Quantum Limit.

Discussion

In our work we studied the application of QFT-based phase estimation algorithm to improve the performance of correlation measurement protocols by increasing its dynamic range for precision spectroscopic measurements. To categorize the application areas of such protocol we classify the sensing scenarios as following: B_rmsγ_eT₂ > 2π and B_rmsγ_eT₂ ≪ 2π. In the latter case, the sensing could not be further improved with phase estimation protocols, since the signal can not saturate the full sensor range even with single qubit register.

In the first case, when the single qubit sensor is saturated, the phase estimation algorithm enhances sensing performance of the system. We further divide the case of classical and quantum signal. With the classical signal, one can use both quantum and semicalssical phase estimation methods such as adaptive or semiclassical QFT, for better usage of available resources comprised of time and qubits. However, the case of a quantum signal is different. Though, there is work showing the possibility for single shot determination of quantum signals using adaptive sensing²⁸, it is subject for further research in application for correlation measurements in nanoscale NMR. The presented QFT-based approach, without intermediate state projection preserves entanglement throughout the protocol, and opens new ways to study the effects of quantum measurements in the saturated sensor regime. In particular, it paves the way to new regimes of generalized measurements with multiqubit register and studies of quantum back-action.

The result of Fig. 2e with sensing of the artificial field show that the QFT brings additional time overhead on the order of 5% to the total operational time. It also brings additional complexity and necessity to have a nuclear spin register, in comparison to the reference⁵, where a quantum phase estimation could be done on single spin. However, when it comes to the correlation protocol, the QFT allows to spare either correlation time between all iterations, or one readout time, thus efficiently reducing overall time. We note that addition of QFT adds roughly 300 μs compared to 15 ms of readout for full register or 8 ms of correlation time.

The analysis of quantum digitizers requires further work, since various aspects of the quantum Shannon theorem like information storage, transfer and extraction with correlation protocol referred as a quantum channel with losses²⁹ could be studied. It has been shown, that NV register can comprise up to ten nuclear qubits³⁰, paving the way to single shot measurements of high dynamic range nanoscale NMR signals. The expected field strength also determines the necessary number of qubits to improve the sensor performance by analysing the saturation condition of most significant qubit ${B}_{max}{\gamma }_{2}{T}_{2}=2\pi {2}^{{n}_{q}^{max}}$. It determines the maximum size of the memory register ${n}_{q}^{max}={{{{{\mathrm{log}}}}}\,}_{2}\frac{{\gamma }_{e}{T}_{2}B}{2\pi }$ for a signal of strength B_max. This means that even small register of 4 qubits is suffice for target field ranges of 7.2 μT for a sensor with a T₂ = 500 μs.

Finally, we compare the performance and areas of applicability with other state-of-the-art nanoscale NMR protocols^12,31,32. We note that, despite a heterodyne approach found to be well suited for some applications it is still limited to long coherent NMR probe objects. Since it could operate at fields where the microwave Rabi frequency is higher than the nuclear spin Larmor frequency. The necessary chemical resolution 1 ppm occurs thus only for long lived coherent NMR probes, while for solids and nanoscale liquid volumes not. In-situ correlation type protocols, on the other side, are beneficial at high magnetic fields, which is useful when the size of the NMR probe is small and its lifetime is shortened e.g. by diffusion. With help of the QFT NV center could realize its quantum sensor potential fully exploiting its quantum computational abilities.

In conclusion, we demonstrated the implementation of QFT using individual solid-state nuclear spins in diamond. Combining QFT with sensing we extended the capability of diamond based quantum sensors and realized a multiqubit phase estimation circuit in a correlation spectroscopy measurement, monitored the dynamics of two target spins with high dynamic range. Their NMR signals were demultiplexed and read out as a separate quantum register outputs. We analyzed the improvement of quantum digitizer with various number of qubits and compare it to a classical ADC. Our results show, that multiple qubit algorithms benefit quantum sensing, and in cases of large time overhead overcomes single qubit protocols in estimation of time varying signals.

Methods

NV center—nuclear spin system

In our experiments we use the single NV electron spin as a sensor that has a long T₂ coherence time T₂ = 430 μs (Hahn echo)²² at ambient conditions at B₀ = 0.7 T.

In implementing the QFT, one needs highly controllable qubit register, which in our case is made of nuclear spins. The nuclear spins that form the co-processor (register) is comprised of the strongly coupled (2.16 MHz) ¹⁴N nuclear spin of the NV center, and two ¹³C nuclear spins (labeled as ¹³C₄₁₄ and ¹³C₉₀) with hyperfine coupling along the quantization axis of the NV center A_zz ≈ 414 kHz and A_zz ≈ 90 kHz, respectively²¹. In total, our register represents an effective 12-level system and allows to implement a variety of quantum protocols including the QFT algorithm. Additionally, a single-shot readout of the individual nuclear spins in the register could be performed^18,21. Due to a comparatively stronger hyperfine couplings stated above all the hyperfine levels could be resolved (twelve lines) in the ODMR spectrum of the NV center which has an ${T}_{2}^{* }$ time about 20 μs. This fulfils the key requirement of our protocol, where the digitized phase is encoded as populations among the 12-levels with a resolution of ϕ/12. The individual addressing of these levels sets the limit to our precision (see Supplementary Information).

Detection of target spins and correlation protocol

A state of the art nanoscale NMR protocol for high magnetic fields is the correlation protocols¹². It consists of two memory assisted sensing steps, encode and decode, separated with a long correlation time T_c. During correlation time the target spins undergo free induction decay or a narrow band RF π pulse. The memory assisted sensing of the spins is realized using NV electron spin and register nuclear spins via entangling operations²². To control t₁ and t₂ nuclear spins we apply resonant RF π pulses of duration 300 μs. They are applied roughly resonant to the frequency of the expected couplings. The Ramsey pulses in Fig. 3 were applied with a π/2 pulse 25 μs (broadband) to initiate the precession of all nuclear spin bath. The RF π pulses as described are applied to target spin system addressing the t₁ and t₂. Their bandwidth could be large and hence the precise knowledge of the frequency is not needed. The sequence is as at the Fig. 3. The U_n is implemented via naturally occurring S_zI_zA_zz interaction between target spins and electron spin similar to previous work²². The data in Fig. 3e was processed using the mathematical fit function using the Python Lmfit library. The best fit function with high R-value (goodness-of-fit measure) was found to be a damped cosine function.

Dynamic range

In a quantum measurement the 2π periodicity of the acquired phase limits the measurement range R_α = π/(∂_αEτ) over which an parameter α could be unambiguously determined. Thus there is a trade-off between the precision (Δ) and measurement range of the measurement (R), represented via a dynamic range (DR = R/Δ). For example, in a sensing protocol (Ramsey type sequence) using n_q uncorrelated qubits one would obtain a dynamic range $D{R}_{SQL}=\frac{\pi }{\tau {\partial }_{\alpha }E}/h\frac{1}{\sqrt{{n}_{q}\cdot {N}_{m}}}\frac{1}{\tau {\partial }_{\alpha }E}=\frac{\pi }{h}\sqrt{{n}_{q}\cdot {N}_{m}}$.

On the other hand, in a phase estimation using the QFT the maximum measurement range R is determined by the smallest phase acquisition time τ. Here the phase could be resolved in the whole 0 − 2π range, and the precision is given by the longest phase acquisition time $\tau \cdot {2}_{q}^{n}$. In that case $D{R}_{QFT}=\frac{2\pi }{\tau {\partial }_{\alpha }E}/h\sqrt{\frac{3}{{N}_{m}({4}_{q}^{n}-1)}}\frac{1}{\tau {\partial }_{\alpha }E}=\frac{2\pi }{\sqrt{3}h}\sqrt{{N}_{m}}\sqrt{({4}_{q}^{n}-1)}\approx 2/\sqrt{3}D{R}_{SQL}\times {2}_{q}^{n}$, where n_q is the number of qubits. In summary, phase estimation using the QFT algorithm will exponentially increase the dynamic range with the number of qubits n_q.

Time varying signal estimation simulation

The simulation of the time varying signal was performed using the QuTIP software package³³. The simulation was performed for both decaying and non-decaying signals. The signal was generated from a dense spectrum having 25 random harmonics with random amplitudes. The signal is shown in Supplementary Figure 3. The SNR of the estimation is determined as root mean square of the actual signal divided by the root mean square of the residual between the actual signal and the estimated value based on measurement outputs. In total, the signal was sampled on 5000 points, while only 200 points were shown for clarity in Fig. 4a, b.