Abstract
Quantum teleportation exemplifies how the transmission of quantum information starkly differs from that of classical information and serves as a key protocol for quantum communication and quantum computing. While an ideal teleportation protocol requires noiseless quantum channels to share a pure maximally entangled state, the reality is that shared entanglement is often severely degraded due to various decoherence mechanisms. Although the quantum noise induced by the decoherence is indeed a major obstacle to realizing a near-term quantum network or processor with a limited number of qubits, the methodologies considered thus far to address this issue are resource-intensive. Here, we demonstrate a protocol that allows optimal quantum teleportation via noisy quantum channels without additional qubit resources. By analyzing teleportation in the framework of generalized quantum measurement, we optimize the teleportation protocol for noisy quantum channels. In particular, we experimentally demonstrate that our protocol enables to teleport an unknown qubit even via a single copy of an entangled state under strong decoherence that would otherwise preclude any quantum operation. Our work provides a useful methodology for practically coping with decoherence with a limited number of qubits and paves the way for realizing noisy intermediate-scale quantum computing and quantum communication.
Similar content being viewed by others
Introduction
Quantum teleportation is a process of transmitting an arbitrary unknown quantum state via a quantum and a classical channel1. The quantum channel is served by an entangled state shared between the sender and receiver. This not only exemplifies how starkly quantum information differs from classical information but also provides a fundamental building block for various protocols in both quantum communication2 and quantum computing3,4. Quantum teleportation was first demonstrated for a photonic qubit5,6 and optical coherent states7, and later teleportation with complete Bell-state measurement was demonstrated8. In recent years, teleportation of photonic qubits over long distances9,10 and of more complex quantum states have been reported11,12. Moreover, quantum teleportation has also been demonstrated for atomic13,14 and solid-state quantum systems15,16. Recently, CNOT gate teleportation17,18, teleportation for distributed nodes19, and teleportation for chip-to-chip communication20 have been demonstrated as potential functionalities for scalable quantum architectures.
The basic requirement for an ideal teleportation process is a noiseless quantum channel established by sharing a pure maximally entangled state such as the Bell state21,22. However, shared entanglement is often severely degraded in reality due to various decoherence mechanisms resulting in mixed entangled states23, seriously deteriorating the performance of the teleportation as a result. The quantum noises and errors induced by decoherence are indeed a major obstacle to constructing a quantum network or connecting components in a scalable quantum architecture. To that end, entanglement purification offers a probabilistic method of preparing a pair of qubits with an increased amount of entanglement, but at the expense of many identically pre-prepared entangled qubits in conjunction with local operations and classical communications24,25,26,27,28. A strategy based on quantum error correction also allows protecting qubits over a noisy channel but requires many qubits in entanglement29,30. Very recently, classical post-processing has been used to mitigate the effect of errors in estimating an expectation value without requiring ancillary qubits31,32,33; however, such a technique is not applicable for the transfer of quantum information via a noisy channel.
In this work, we demonstrate a protocol that allows optimal quantum teleportation via noisy quantum channels without additional qubits. In contrast to the previous schemes relying on entanglement purification or quantum error correction which are resource-intensive, it is possible in our protocol to teleport an unknown qubit through a single copy of a decohered entangled state. By analyzing quantum teleportation via noisy quantum channels in the framework of generalized quantum measurement, we find that there exists a joint measurement (analogous to the Bell-state measurement) and the corresponding single-qubit reversing operation, which together achieve optimal quantum teleportation with a substantially enhanced teleportation fidelity. The reversing operation here is chosen to optimally mitigate the effect of noise in the quantum channel. In particular, we experimentally demonstrate that our protocol enables quantum teleportation even via highly noisy quantum channels (i.e., an entangled state under strong decoherence) that would otherwise preclude any quantum operations.
Results
Protocol
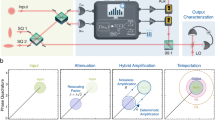
Consider the schematic of quantum teleportation via noisy quantum channels as shown in Fig. 1. Alice has an arbitrary unknown quantum state ρa which she wishes to transmit to Bob without physically transporting the qubit. An entangled state \({\left|{{\Psi }}\right\rangle }_{AB}\) is distributed to Alice and Bob via noisy quantum channels, resulting in sharing a mixed entangled state \({\mathcal{E}}({\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|)\), where \({\mathcal{E}}=\{{\hat{E}}^{k}\}\) represents the decoherence channel with \({\hat{E}}^{k}\) denoting the Kraus operator for the noise operation. For teleportation, Alice performs joint measurement on the basis \(\{{\left|{W}_{r}\right\rangle }_{aA}\}\) on qubit a with the state ρa and qubit A of the mixed entangled state \({\mathcal{E}}({\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|)\) shared between Alice and Bob. In the framework of generalized quantum measurement, the noisy channel and the joint measurement together constitute an effective generalized quantum measurement. That is, after the joint measurement, the reduced state in mode B can be written as
for the outcome r. Here, we define an effective operator \({\hat{M}}_{r,a\to B}^{k}\equiv aA\left\langle {W}_{r}\right|{\hat{E}}^{k}{\left|{{\Psi }}\right\rangle }_{AB}\), satisfying the completeness relation, \({\sum }_{r,k}{\hat{M}}_{r}^{k\dagger }{\hat{M}}_{r}^{k}=1\), to represent quantum measurement whose input (a) and output (B) modes are spatially separated. The measurement outcome r is then sent to Bob via a classical channel and Bob performs an appropriate reversing operation \({\hat{R}}_{B}^{r}\) to obtain an output state ρB, i.e., \({\hat{R}}_{B}^{r}({\sum }_{k}{\hat{M}}_{r,a\to B}^{k}{\rho }_{a}{\hat{M}}_{r,a\to {B}^{\dagger }}^{k}){\hat{R}}_{{B}^{\dagger }}^{r}\propto {\rho }_{B}\). Here, the reversing operation is designed to reverse the effective quantum measurement by a non-unitary operation. As the effective quantum measurement encapsulates the joint measurement and the entangled state distributed via a noisy quantum channel, the reversing operation can be optimized relying on the prior information on the noise affecting the entangled state.
The Bell state \({\left|{{\Psi }}\right\rangle }_{AB}\) is shared between Alice and Bob via a noisy quantum channel, resulting in a mixed entangled state \({\mathcal{E}}({\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|)\). Alice wants to teleport ρa to Bob. The noisy channel and the joint measurement together constitute an effective generalized quantum measurement (Ma→B). Conditioned on the outcome of the effective quantum measurement on Alice’s qubits, an appropriate reversing operation (R) is applied to Bob’s qubit that ends up in the state ρB. Appropriate joint measurement and reversing operation enable us to achieve optimal teleportation via highly noisy quantum channels.
Our teleportation protocol can be thus generally represented by a quantum measurement Ma→B and its reversal process R, i.e., (R∘Ma→B)(ρa) ∝ ρB34,35. This framework encompasses all the previously proposed teleportation protocols, in which the reversing operation is limited to a conditional unitary operation \({\hat{R}}^{r}={\hat{U}}^{r}\) (referred to as the conventional teleportation protocols in what follows). It recovers the original teleportation protocol if the joint measurement is performed on the Bell basis and Bob applies a conditional Pauli operation.
Our teleportation protocol can be optimized for a given quantum channel \({\mathcal{E}}({\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|)\) by modifying the joint measurement performed by Alice and the reversing operation performed by Bob (i) to maximize the average teleportation fidelity F, indicating the closeness between the input ρa and the teleported state ρB, and then (ii) to maximize the overall success probability P as well for the given fidelity (see Supplementary Note 1 for details). For a noiseless channel, we can always find protocols to recover the input state faithfully \({\hat{R}}^{r}{\hat{M}}_{r}\rho {\hat{M}}_{{r}^{\dagger }}{\hat{R}}^{r\dagger }\propto \rho\), i.e., F = 1. The protocol can be then optimized such that the success probability P reaches up to the fundamental limit in terms of the trade-off relation between P and the amount of extracted information G by Ma→B, i.e., 6G + P ≤ 435,36,37,38,39. It implies that the more information is extracted by Ma→B, the less possible the teleportation succeeds. In the presence of noise, we optimize the protocol to yield the maximum teleportation fidelity
where \(p(r,\psi )={\sum }_{k}\left\langle \psi \right|{\hat{M}}_{r,a\to {B}^{\dagger }}^{k}{\hat{M}}_{r,a\to B}^{k}\left|\psi \right\rangle\) is the probability obtaining the outcome r and ρB(r) is the output state when the teleportation succeeds (here we assume a pure input state \(\left|\psi \right\rangle\) for simplicity, but the definitions are generally valid for any input state). The teleportation fidelity exceeding the classical limit F > 2/3 ensures genuine quantum teleportation of a qubit via a noisy channel.
In what follows, we shall first experimentally demonstrate that our protocol allows the teleportation fidelity F = 1 and saturates the trade-off relation, 6G + P = 4, via noiseless quantum channels. This demonstration involves a pure non-maximally entangled state between Alice and Bob. Note that, for a pure non-maximally entangled channel, the original teleportation protocol does not yield F = 1. Moreover, probabilistic protocols proposed so far to achieve F = 1 either uses ancillary qubits40, requires nontrivial joint measurement41, or is unable to reach the maximum bound of P in view of 6G + P = 442. Then, we demonstrate that our protocol enables quantum teleportation with fidelity beyond the classical limit even via highly noisy quantum channels that would make it impossible to perform teleportation with conventional protocols.
Experimental demonstration
The experimental schematic for demonstrating optimal teleportation via noisy quantum channels is shown in Fig. 2a. Ultrafast femtosecond laser pulses are used to pump spontaneous parametric down-conversion (SPDC) processes to prepare a pair of polarization-entangled photonic qubits in modes A and B as \({\left|{{\Psi }}\right\rangle }_{AB}=({\left|00\right\rangle }_{AB}+{\left|11\right\rangle }_{AB})/\sqrt{2}\)43,44,45 and to prepare a heralded single-photon polarization state in mode a as \({\left|\psi \right\rangle }_{a}=\alpha {\left|0\right\rangle }_{a}+\beta {\left|1\right\rangle }_{a}\)37,39. Here, \(\left|0\right\rangle\) and \(\left|1\right\rangle\) denote the horizontal and vertical polarization states, respectively. A partial polarizing beam splitter (PPBS1) is used to prepare a pure non-maximally entangled state46. In the experiment, we have investigated the amplitude damping channel as this particular decoherence model allows us to control the amount of decoherence easily and accurately for the polarization-entangled state shared between Alice and Bob47,48,49,50. The joint measurement is based on the two-photon quantum interference of two independent single photons a and A51,52. Indistinguishability of these photons is the key to the successful joint measurement and is demonstrated in Fig. 2b via the high visibility of two-photon interference (visibility of 0.97). For the joint measurement of the polarization qubits in modes a and A, similarly to Bell-state measurement8, there are four possible measurement outcomes r = {1, 2, 3, 4}, see Fig. 2 and Eq. (1), each corresponding to a specific joint measurement basis \({\left|{W}_{r}\right\rangle }_{aA}\). Depending on the measurement outcome r, an appropriate reversing operation should be applied for photon B. See “Methods” for more details on the experimental setup.
a Schematic of the experimental setup. The initial polarization qubit is prepared by the heralded single-photon source in mode a. The polarization-entangled Bell state is prepared in modes A and B via spontaneous parametric down-conversion. A partial polarizing beam splitter (PPBS1) is used to prepare a pure non-maximally entangled state. The noisy channel implements amplitude damping decoherence, but our protocol applies to all other forms of quantum errors. Joint measurement is performed on photon A and photon a. The reversing operation is appropriately designed for the amplitude damping channel and the joint measurement outcome. The qubit state at Bob is analyzed via quantum state tomography. BBO barium borate nonlinear crystal, HWP half-wave plate, QWP quarter-wave plate, IF interference filter, FM flip mirror, BS beam splitter, PBS polarizing beam splitter, PPBS partially polarizing beam splitter, BD beam displacer. b Two-photon interference (visibility of 0.97) demonstrating indistinguishability between photon A and heralded photon a using 2-nm interference filters. The red solid circles represent fourfold coincidence count rates among detectors D1, D4, DT, and DB for 60 s of accumulation time. Here, DB is placed in front of PPBS1. The solid line represents the Gaussian fit to the data.
We first describe the experimental demonstration of our protocol when a pure non-maximally entangled state \({\left|{{\Psi }}\right\rangle }_{AB}=\cos (\theta /2){\left|00\right\rangle }_{AB}+\sin (\theta /2){\left|11\right\rangle }_{AB}\) is shared via a noiseless quantum channel, where 0 ≤ θ ≤ π/2. In this case, the teleportation fidelity of unity can be achieved, and while maintaining F = 1 the maximal success probability P is also attained to saturate the trade-off relation 6G + P = 438. For instance, consider a measurement outcome on the basis \({\left|{W}_{1}\right\rangle }_{aA}=\cos (\phi /2){\left|00\right\rangle }_{aA}+\sin (\phi /2){\left|11\right\rangle }_{aA}\). According to Eq. (1), the effective quantum measurement is given as \({\hat{M}}_{1}{ = }_{aA}{\left\langle {W}_{r}| {{\Psi }}\right\rangle }_{AB}=\cos (\theta /2)\cos (\phi /2){\left|0\right\rangle }_{Ba}\left\langle 0\right|+\sin (\theta /2)\sin (\phi /2){\left|1\right\rangle {}_{B}}_{a}\left\langle 1\right|\). Then, the corresponding reversing operation is found to be \({\hat{R}}_{B}^{1}={\hat{U}}^{1}(\tan (\theta /2)\tan (\phi /2)\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|)\) for θ ≤ ϕ. Here, \({\hat{U}}^{r}\) is the unitary operator determined by the measurement outcome r and, for r = 1, \({\hat{U}}^{r}\) is the identity operator. Therefore, the effective quantum measurement \({\hat{M}}_{1}\) and the reversing operation \({\hat{R}}_{B}^{1}\) applied to the three qubits a, A, and B, respectively, destroys the qubit state of a photon a and faithfully reconstructs it at photon B, i.e., \({\hat{R}}_{B}^{1}{\hat{M}}_{1}{\left|\psi \right\rangle }_{a}=\sin (\theta /2)\sin (\phi /2)(\alpha {\left|0\right\rangle }_{B}+\beta {\left|1\right\rangle }_{B})\). In the experiment, the joint measurement basis was chosen to be the Bell basis by setting ϕ = π/2 to easily satisfy the condition θ ≤ ϕ for arbitrary values of θ (0 ≤ θ ≤ π/2). The reversing operation was implemented with beam displacers (BD) and half-wave plates (HWPs). We find the average fidelity as we chose six initial states in mutually unbiased bases on the Bloch sphere, i.e., \(\left|0\right\rangle\), \(\left|1\right\rangle\), \(\left|+\right\rangle =(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}\), \(\left|-\right\rangle =(\left|0\right\rangle -\left|1\right\rangle )/\sqrt{2}\), \(\left|+i\right\rangle =(\left|0\right\rangle +i\left|1\right\rangle )\sqrt{2}\), and \(\left|-i\right\rangle =(\left|0\right\rangle -i\left|1\right\rangle )/\sqrt{2}\)53.
In order to experimentally obtain G by the effective quantum measurement and P by the reversing operation, quantum teleportation is performed for all four joint measurements (not simultaneously, but two at a time), see “Methods” for details on evaluating G and P. Figure 3a shows the experimentally obtained trade-off relation between G and P for five different pure non-maximally entangled states. It is clear that our teleportation protocol saturates the trade-off relation 6G + P = 4, i.e., is optimal in the sense that the performance of the teleportation reaches the fundamental upper bound34. The result demonstrates that “the more information on the input state is extracted by Alice, the less possible the teleportation becomes successful”. The teleportation fidelity, which can be estimated by performing quantum state tomography (QST) between the input qubit states in mode a and of the teleported qubit states in mode B, in the cases of sharing a Bell state or other pure non-maximally entangled states have also been obtained, see, for example, Fig. 3b, c. The teleportation fidelity always far exceeds the classical limit of 2/3: Fig. 3b, c exhibits the average fidelities of 0.938 and 0.915, respectively. Slightly reduced fidelity from the ideal value of 1 can be attributed to a number of experimental imperfections, e.g., the fidelity of 0.98 for shared entangled states, lowered two-photon visibility of 0.97 due to remaining partial distinguishability of the photons for the joint measurement, and the interferometric reversing operation with the visibility of 0.96. See Supplementary Note 2 for further details.
a The success probability of teleportation versus the information gain by Alice. Red solid line represents the ideal trade-off relation and red solid circles show the values for pure non-maximally entangled states shown in the inset. The corresponding experimental data are shown with green solid circles. The error bars represent one standard deviation. Teleportation fidelity in the case of sharing b the Bell state \(\sqrt{0.5}\left|00\right\rangle +\sqrt{0.5}\left|11\right\rangle\) and c the pure non-maximally entangled state \(\sqrt{0.56}\left|00\right\rangle +\sqrt{0.44}\left|11\right\rangle\) for the joint measurement basis \({\left|{W}_{1}\right\rangle }_{aA}=(\left|00\right\rangle +\left|11\right\rangle )/\sqrt{2}\). The dashed lines show the classical limit of 2/3.
We now describe the demonstration of the optimal teleportation via an entangled state under strong decoherence. Here, we consider the amplitude damping in mode B. Note that this framework is generally applicable to the decoherence in mode A and also for the dephasing and depolarizing decoherence34. For this demonstration, the decoherence channel is inserted in the path of photon B, at the same time removing PPBS1, see Fig. 2: the mixed entangled state shared between A and B is given as \(\left(\right.{\left|00\right\rangle }_{AB}+\sqrt{1-D}{\left|11\right\rangle }_{AB}\left)\right.{\left(\right.}_{AB}\left\langle 00\right|+{\sqrt{1-D}}_{AB}\left\langle 11\right|\left)\right./2+(D/2){\left|10\right\rangle }_{AB}\left\langle 10\right|\), where D is the degree of decoherence. After the joint measurement in the basis \({\left|{W}_{r}\right\rangle }_{aA}\) with the measurement outcome r, the reversing operation \({\hat{U}}^{r}(\sqrt{1-D}\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|)\) is applied to optimally reconstruct the initial state of qubit a at mode B. See “Methods” for further details.
Figure 4 presents both the theoretically and experimentally obtained average teleportation fidelities F by varying degrees of decoherence D. The colored region in Fig. 4 represents the available teleportation fidelities by our protocol beyond the reach of the conventional protocols based on the unitary reversing operation. The experimental results clearly demonstrate that our protocol enables quantum teleportation even via an entangled state under strong decoherence that would otherwise preclude any quantum operations. For instance, if D ≥ 0.5, the mixed entangled state would not violate Bell’s inequality54. However, even for very strong decoherence values of D = 0.74 and D = 0.92 shown in Fig. 4, our protocol allows to teleport unknown quantum states significantly beyond the classical limit F > 2/3. Note that, for amplitude damping decoherence, our teleportation protocol achieves even higher teleportation fidelities if Alice and Bob share a pure non-maximally entangled state. The teleportation fidelity can be enhanced arbitrarily close to unity by decreasing the success probability depending on how much the channel has decohered. The experimental results and detailed analysis for this specific case are presented in Supplementary Note 3.
Teleportation fidelities achieved over noisy quantum channels. We here consider the amplitude damping decoherence on the maximally entangled two-qubit channel. The solid lines represent the theoretical upper bounds of the average fidelities for our protocol (red) and the conventional teleportation protocol (blue) based on the unitary reversing operation, respectively, while the dashed lines are drawn, including experimental imperfections. The colored region represents the available teleportation fidelities by our protocol beyond the reach of convention teleportation protocols. The red solid circles are the experimental data based on our protocol, with the error bars representing one standard deviation. The results clearly demonstrate that our protocol enables teleportation even via a single copy of an entangled state under strong decoherence that would otherwise preclude any quantum operations.
Discussion
We have proposed and experimentally demonstrated a protocol for optimal quantum teleportation via noisy quantum channels, which does not require any additional qubits. We have shown that quantum teleportation can be generally optimized in the framework of generalized quantum measurements and corresponding reversing operations. This approach allows to teleport an unknown qubit via a single copy of an entangled state under strong decoherence that would otherwise preclude any quantum operations. In particular, we have experimentally demonstrated that our protocol enables quantum teleportation even through highly noisy quantum channels, overcoming the limit of the conventional teleportation protocols based on the unitary reversing operation.
In order to cope with the effects of noise in the quantum channel during quantum teleportation, two different approaches may be considered. One approach is to recover the entangled state from the effect of noise to carry out the conventional teleportation protocol. Schemes to recover two-qubit entanglement from the noise in the quantum channel include entanglement distillation/concentration24,25,26,28, protecting entanglement by weak measurement and reversal49, and controlling open quantum system55,56,57. The other approach is to modify the teleportation protocol itself to adapt to the noisy quantum channel40,42. In this work, by analyzing teleportation in the framework of generalized quantum measurement, we optimize the teleportation protocol itself for noisy quantum channels41, offering clear advantages over the above-mentioned approaches. Unlike entanglement concentration/purification schemes, multiple copies of identically decohered two-qubit entangled states are not required and our teleportation protocol achieves optimal quantum teleportation (i.e., saturating the fundamentally achievable fidelity and maximizing the success probability for a given fidelity) of an unknown qubit via a single copy of an entangled state under strong decoherence that would otherwise preclude any quantum operations. Similarly to other approaches for tackling decoherence in quantum information processing, our optimal quantum teleportation protocol requires prior information of the channel noise so as to determine proper quantum measurement and reversing operation: recent advances in quantum process tomography58,59 and noise characterization techniques60,61 offer systematic and efficient approaches for obtaining the information about the quantum noise in the channel.
While there has been immense progress in quantum information processing and long-distance quantum communication in recent years, degradation of entanglement due to noise remains to be an important issue to address in constructing scalable quantum systems. Our work provides insights into practically coping with decoherence with a limited number of qubits and paves the way for realizing noisy intermediate-scale quantum technologies. Potential directions of future research include entanglement-based quantum communication (e.g., long-distance quantum teleportation, deterministic secure quantum communication, etc.) and distributed quantum information processing in a noisy environment.
Methods
Details on the experimental setup
The SPDC process was pumped by a 390-nm centered ultrafast pulse (~140 fs) and the central wavelength of the SPDC photons is 780 nm. The polarization-entangled photonic qubit pair, \({\left|{{\Psi }}\right\rangle }_{AB}=({\left|00\right\rangle }_{AB}+{\left|11\right\rangle }_{AB})/\sqrt{2}\), was then prepared by using two 1-mm thick type-II BBO crystals, in the frequency-degenerate beamlike SPDC configuration, with a HWP sandwiched between them and a set of compensating crystals to remove spatial and temporal distinguishability43,44,45. The generated polarization-entangled qubit pair is shared between Alice and Bob.
The arbitrary initial state \({\left|\psi \right\rangle }_{a}\) to be teleported from Alice to Bob was prepared by using another 1-mm thick BBO crystal in the frequency-degenerate beamlike SPDC configuration. One photon of the SPDC photon pair is detected at DT, heralding the presence of a single photon in mode a. The polarization qubit state for the single photon in mode a, \({\left|\psi \right\rangle }_{a}\), was then prepared by using the set of HWP and QWP. Joint measurement of qubits a and A was implemented by two-photon quantum interference and coincidence detection51,52. To improve quantum interference, 2 nm full-width at half-maximum interference filters were used in front of all detectors to further reduce any remaining spectral/temporal distinguishability between the two single photons.
The joint measurement between photons a and A, analogous to the Bell measurement in conventional teleportation protocols, is to be performed in the following basis set: \({\left|{W}_{1}\right\rangle }_{aA}=\cos (\phi /2)\left|00\right\rangle +\sin (\phi /2)\left|11\right\rangle\), \({\left|{W}_{2}\right\rangle }_{aA}=\sin (\phi /2)\left|00\right\rangle -\cos (\phi /2)\left|11\right\rangle\), \({\left|{W}_{3}\right\rangle }_{aA}=\cos (\phi /2)\left|01\right\rangle +\sin (\phi /2)\left|10\right\rangle\), and \({\left|{W}_{1}\right\rangle }_{aA}=\sin (\phi /2)\left|01\right\rangle -\cos (\phi /2)\left|10\right\rangle\). In the experiment, by setting the HWP1 angle in Fig. 2a at φ1 = π/4, joint measurement between detectors D1–D2 or D3–D4 implements \({}_{aA}\left\langle {W}_{1}\right|\) measurement and joint measurement between detectors D1–D3 or D2–D4 implements \({}_{aA}\left\langle {W}_{2}\right|\) measurement. For the remaining two joint measurements \({}_{aA}\left\langle {W}_{3}\right|\) and \({}_{aA}\left\langle {W}_{4}\right|\), they are similarly performed by setting φ1 = 0.
The amplitude damping decoherence channel is given by \({\mathcal{E}}({\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|)={\hat{E}}^{1}{\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|{\hat{E}{}^{1}}^{\dagger }+{\hat{E}}^{2}{\left|{{\Psi }}\right\rangle }_{AB}\left\langle {{\Psi }}\right|{\hat{E}{}^{2}}^{\dagger }\), where the Kraus operators are \(\{{\hat{E}}^{1}=\left|0\right\rangle \left\langle 0\right|+\sqrt{1-\,\text{D}\,}\left|1\right\rangle \left\langle 1\right|,\,{\hat{E}}^{2}=\sqrt{\,\text{D}\,}\left|0\right\rangle \left\langle 1\right|\}\). In experiment, \({\hat{E}}^{1}\) is implemented by a partial polarizing beam splitter PPBS2 and \({\hat{E}}^{2}\) is implemented by reflection at PPBS2 and HWP at π/4. Incoherent mixing of the two processes results in the amplitude damping decoherence channel.
Consider a pure arbitrary entangled state \({\left|{{\Psi }}\right\rangle }_{AB}=\cos (\theta /2){\left|00\right\rangle }_{AB}+\sin (\theta /2){\left|11\right\rangle }_{AB}\) with 0 ≤ θ ≤ π/2 as the quantum channel, where mode B experiences the amplitude damping decoherence, and assume that the joint measurement is performed on the Bell basis (ϕ = π/2). According to Eq. (1), the effective quantum measurement is then described by a set of operators:
An arbitrary measurement operator can be presented by the singular value decomposition as \({\hat{M}}_{r}={\hat{V}}_{r}{\hat{D}}_{r}{\hat{U}}_{r}\) with unitary operators, \({\hat{V}}_{r}\) and \({\hat{U}}_{r}\) and a diagonal matrix \({\hat{D}}_{r}=\mathop{\sum }\nolimits_{n = 0}^{d-1}{\lambda }_{n}^{r}\left|{v}_{n}^{r}\right\rangle \left\langle {v}_{n}^{r}\right|\), where \(\{\left|{v}_{n}^{r}\right\rangle | n=0,\ldots ,d-1\}\) is the orthonormal basis. Here we assume that, without loss of generality, the diagonal elements \({\lambda }_{n}^{r}\), i.e., singular values are put in decreasing order, i.e., \({\lambda }_{0}^{r}\ge {\lambda }_{1}^{r}\ge \ldots \ge {\lambda }_{d-1}^{r}\). The optimal reversing operator is then given by \({\hat{R}}^{r}={\lambda }_{d-1}^{r}{\hat{U}}_{r}^{\dagger }{\hat{D}}_{r}^{-1}{\hat{V}}_{r}^{\dagger }\), s.t., \({\hat{R}}^{r}{\hat{M}}_{r}\left|\psi \right\rangle ={\lambda }_{d-1}^{r}\left|\psi \right\rangle\) and \(P={\sum }_{r}{({\lambda }_{d-1}^{r})}^{2}\)38.
In the presence of noise, the input state \(\left|\psi \right\rangle\) is changed to \({\sum }_{k}{\hat{M}}_{r}^{k}\left|\psi \right\rangle \left\langle \psi \right|{\hat{M}}_{r}^{k\dagger }\) after the joint measurement as given in Eq. (1). In this case, the optimal reversing operator for the outcome r is given by \({\hat{R}}^{r}={\lambda }_{d-1}^{r,{k}_{m}}{\hat{U}}_{r,{k}_{m}}^{\dagger }{\hat{D}}_{r,{k}_{m}}^{-1}{\hat{V}}_{r,{k}_{m}}^{\dagger }\), where km yields the maximum smallest singular value, i.e., \({\lambda }_{d-1}^{r,{k}_{m}}\equiv \mathop{\max }\limits_{k}[{\lambda }_{d-1}^{r,k}]\)34.
For the effective quantum measurement in Eq. (3), the optimal reversing operator is given by the form \({\hat{R}}^{r}={\hat{U}}^{r}(\tan (\theta /2)\sqrt{1-D}\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|)\), where \({\hat{U}}^{r}=\{\hat{I},{\sigma }_{z},{\sigma }_{x},{\sigma }_{x}{\sigma }_{z}\}\) for r = {1, 2, 3, 4}. In the experiment, as \(\left|0\right\rangle\) and \(\left|1\right\rangle\) are encoded in the polarization states \(\left|H\right\rangle\) and \(\left|V\right\rangle\), respectively, the reversing operation can be implemented with a Mach–Zehnder interferometer built with polarization-dependent beam displacers and half-wave plates as shown in Fig. 2a. The Mach–Zehnder interferometer implements \({\cos }^{2}(2{\varphi }_{2})\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|\), where φ2 is the angle of HWP2.
Evaluation of information gain and success probability
Assume a quantum measurement, described by a set of operators \(\{{\hat{M}}_{r}\}\), applied to an arbitrary input state \(\left|\psi \right\rangle\) (a pure input state is considered for simplicity, but the definition is valid for any mixed states). To quantify the information gain G, we use the mean estimation fidelity36. In every trial, we can make a guess that the input state is \(\left|{\phi }_{r}\right\rangle\) for the outcome r. The quality of the guess can be evaluated by \(| \left\langle \psi | {\phi }_{r}\right\rangle {| }^{2}\). By averaging this over all possible input states and outcomes, we can define the information gain as \(G=\int d\psi {\sum }_{r}\left\langle \psi \right|{\hat{M}}_{r}^{\dagger }{\hat{M}}_{r}\left|\psi \right\rangle | \left\langle \psi | {\phi }_{r}\right\rangle {| }^{2}\). For the effective measurement in Eq. (3) with D = 0, the information gain is evaluated as \(G=(1+{\cos }^{2}(\theta /2))/3\).
In experiment, G is estimated from the fourfold coincidence counts involving the detector DG, the heralding detector DT, and the joint measurement detectors shown in Fig. 2a. The probability of state projection is evaluated from the ratio of fourfold coincidences as \(\left\langle \psi \right|{\hat{M}}_{r}^{\dagger }{\hat{M}}_{r}\left|\psi \right\rangle /({\sum }_{r}\left\langle \psi \right|{\hat{M}}_{r}^{\dagger }{\hat{M}}_{r}\left|\psi \right\rangle )\), where r = {1, 2, 3, 4}. The quality of guess \(| \left\langle \psi | {\phi }_{r}\right\rangle {| }^{2}\) is obtained by calculating with the optimal guessing state, i.e., the eigenstate of a measurement operator corresponding to the largest eigenvalue36. The average fidelity can be obtained by averaging any six input states forming a regular octahedron on Bloch sphere53. Here, six input states \(\left|0\right\rangle\), \(\left|1\right\rangle\), \(\left|+\right\rangle\), \(\left|-\right\rangle\), \(\left|+i\right\rangle\), and \(\left|-i\right\rangle\) are used for evaluating the average fidelity.
In a noiseless scenario, an appropriate reversing operation chosen for each measurement operator can recover the input state faithfully, s.t., \({\hat{R}}^{r}{\hat{M}}_{r}\left|\psi \right\rangle ={\eta }_{r}\left|\psi \right\rangle\), where ∣ηr∣2 is the success probability for each r. The maximum overall success probability of reversing operation is then given by \(P=\max {\sum }_{r}| {\eta }_{r}{| }^{2}\). It was shown that the information gain and the success probability of reversing operation for a quantum measurement are in a trade-off relation as d(d + 1)G + (d − 1)P ≤ 2d in arbitrary d-dimensional Hilbert space38. For qubits d = 2, it becomes 6G + P ≤ 4. For the effective measurement in Eq. (3) with D = 0, the maximum success probability of reversing operation is obtained as \(P=2{\sin }^{2}(\theta /2)\).
In the experiment, P is estimated from the fourfold coincidence counts involving the detector DP, the heralding detector DT, and the joint measurement detectors shown in Fig. 2a. Similarly as before, the probability of successful teleportation is evaluated from the ratio of fourfold coincidences as \(\left\langle \psi \right|{\hat{M}}_{r}^{\dagger }{\hat{R}{}^{r}}^{\dagger }{\hat{R}}^{r}{\hat{M}}_{r}\left|\psi \right\rangle /({\sum }_{r}\left\langle \psi \right|{\hat{M}}_{r}^{\dagger }{\hat{M}}_{r}\left|\psi \right\rangle )\).
Optimal teleportation via noisy quantum channels
Here, we consider optimal teleportation via a maximally entangled state under amplitude damping decoherence (on mode B). If the joint measurement is performed on \({\left|{W}_{1}\right\rangle }_{aA}=({\left|00\right\rangle }_{aA}+{\left|11\right\rangle }_{aA})/\sqrt{2}\), the effective quantum measurement is given as \({\hat{M}}_{1}^{1}=({\left|0\right\rangle {}_{B}}_{a}\left\langle 0\right|+\sqrt{1-D}{\left|1\right\rangle {}_{B}}_{a}\left\langle 1\right|)/2\) and \({\hat{M}}_{1}^{2}=(\sqrt{D}/2){\left|0\right\rangle {}_{B}}_{a}\left\langle 1\right|\) from Eq. (3). The corresponding reversing operator is \({\hat{R}}_{B}^{1}={\hat{U}}^{1}(\sqrt{1-D}\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|)\), where \({\hat{U}}^{1}=\hat{I}\). Then, the final output state at mode B is given by \({\rho }_{B}=(1-D)(\alpha {\left|0\right\rangle }_{B}+\beta {\left|1\right\rangle }_{B})({{\alpha }^{* }}_{B}\left\langle 0\right|+{{\beta }^{* }}_{B}\left\langle 1\right|)/4+D(1-D)| \beta {| }^{2}{\left|0\right\rangle }_{BB}\left\langle 0\right|/4\).
Data availability
Data are available from the corresponding authors upon reasonable request.
References
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413 (2001).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390 (1999).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46 (2001).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575 (1997).
Boschi, D., Branca, S., De Martini, F., Hardy, L. & Popescu, S. Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 80, 1121 (1998).
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706 (1998).
Kim, Y.-H., Kulik, S. P. & Shih, Y. Quantum teleportation of a polarization state with a complete bell state measurement. Phys. Rev. Lett. 86, 1370 (2001).
Ma, X.-S. et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269 (2012).
Ren, J.-G. et al. Ground-to-satellite quantum teleportation. Nature 549, 70 (2017).
Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516 (2015).
Graham, T. M., Bernstein, H. J., Wei, T.-C., Junge, M. & Kwiat, P. G. Superdense teleportation using hyperentangled photons. Nat. Commun. 6, 7185 (2015).
Barrett, M. Deterministic quantum teleportation of atomic qubits. Nature 429, 737 (2004).
Olmschenk, S. et al. Quantum teleportation between distant matter qubits. Science 323, 486 (2009).
Steffen, L. et al. Deterministic quantum teleportation with feed-forward in a solid state system. Nature 500, 319 (2013).
Pfaff, W. et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532 (2014).
Chou, K. S. et al. Deterministic teleportation of a quantum gate between two logical qubits. Nature 561, 368 (2018).
Wan, Y. et al. Quantum gate teleportation between separated qubits in a trapped-ion processor. Science 364, 875 (2019).
Lee, S. M., Lee, S.-W., Jeong, H. & Park, H. S. Quantum teleportation of shared quantum secret. Phys. Rev. Lett. 124, 060501 (2020).
Llewellyn, D. et al. Chip-to-chip quantum teleportation and multi-photon entanglement in silicon. Nat. Phys. 16, 148 (2020).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337 (1995).
Kim, Y.-H., Kulik, S. P., Chekhova, M. V., Grice, W. P. & Shih, Y. Experimental entanglement concentration and universal bell-state synthesizer. Phys. Rev. A 67, 010301 (2003).
White, A. G., James, D. F. V., Munro, W. J. & Kwiat, P. G. Exploring Hilbert space: accurate characterization of quantum information. Phys. Rev. A 65, 012301 (2001).
Bennett, C. H., Bernstein, H. J., Popescu, S. & Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046 (1996).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722 (1997).
Pan, J.-W., Gasparoni, S., Ursin, R., Weihs, G. & Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 423, 417 (2003).
Yamamoto, T., Koashi, M., Özdemir, S. K. & Imoto, N. Experimental extraction of an entangled photon pair from two identically decohered pairs. Nature 421, 343 (2003).
Zhao, Z., Yang, T., Chen, Y.-A., Zhang, A.-N. & Pan, J.-W. Experimental realization of entanglement concentration and a quantum repeater. Phys. Rev. Lett. 90, 207901 (2003).
Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 6, 6787 (2015).
Lee, S.-W., Ralph, T. C. & Jeong, H. Fundamental building block for all-optical scalable quantum networks. Phys. Rev. A 100, 052303 (2019).
Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509 (2017).
Li, Y. & Benjamin, S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7, 021050 (2017).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491 (2019).
Lee, S.-W., Im, D.-G., Kim, Y.-H., Nha, H. & Kim, M. S. Quantum teleportation is a reversal of quantum measurement. Preprint at https://arxiv.org/abs/2104.12178 (2021).
Lee, S.-W., Kim, J. & Nha, H. Complete information balance in quantum measurement. Quantum 5, 414 (2021).
Banaszek, K. Fidelity balance in quantum operations. Phys. Rev. Lett. 86, 1366 (2001).
Baek, S.-Y., Cheong, Y.-W. & Kim, Y.-H. Minimum-disturbance measurement without postselection. Phys. Rev. A 77, 060308 (2008).
Cheong, Y. W. & Lee, S.-W. Balance between information gain and reversibility in weak measurement. Phys. Rev. Lett. 109, 150402 (2012).
Lim, H.-T., Ra, Y.-S., Hong, K.-H., Lee, S.-W. & Kim, Y.-H. Fundamental bounds in measurements for estimating quantum states. Phys. Rev. Lett. 113, 020504 (2014).
Li, W.-L., Li, C.-F. & Guo, G.-C. Probabilistic teleportation and entanglement matching. Phys. Rev. A 61, 034301 (2000).
Son, W., Lee, J., Kim, M. S. & Park, Y.-J. Conclusive teleportation of a d-dimensional unknown state. Phys. Rev. A 64, 064304 (2001).
Agrawal, P. & Pati, A. K. Probabilistic quantum teleportation. Phys. Lett. A 305, 12 (2002).
Takeuchi, S. Beamlike twin-photon generation by use of type II parametric downconversion. Opt. Lett. 26, 843 (2001).
Kim, Y.-H. Quantum interference with beamlike type-II spontaneous parametric down-conversion. Phys. Rev. A 68, 013804 (2003).
Niu, X.-L., Huang, Y.-F., Xiang, G.-Y., Guo, G.-C. & Ou, Z. Y. Beamlike high-brightness source of polarization-entangled photon pairs. Opt. Lett. 33, 968 (2008).
White, A. G., James, D. F. V., Eberhard, P. H. & Kwiat, P. G. Nonmaximally entangled states: production, characterization, and utilization. Phys. Rev. Lett. 83, 3103 (1999).
Almeida, M. P. et al. Environment-induced sudden death of entanglement. Science 316, 579 (2007).
Lee, J.-C., Jeong, Y.-C., Kim, Y.-S. & Kim, Y.-H. Experimental demonstration of decoherence suppression via quantum measurement reversal. Opt. Express 19, 16309 (2011).
Kim, Y.-S., Lee, J.-C., Kwon, O. & Kim, Y.-H. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 8, 117 (2012).
Lee, J.-C. et al. Experimental demonstration of delayed-choice decoherence suppression. Nat. Commun. 5, 4522 (2014).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044 (1987).
Shih, Y. H. & Alley, C. O. New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion. Phys. Rev. Lett. 61, 2921 (1988).
Bowdrey, M. D., Oi, D. K. L., Short, A. J., Banaszek, K. & Jones, J. A. Fidelity of single qubit maps. Phys. Lett. A 294, 258 (2002).
Pramanik, T. et al. Nonlocal quantum correlations under amplitude damping decoherence. Phys. Rev. A 100, 042311 (2019).
Liu, B.-H. et al. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 7, 931 (2011).
Orieux, A. et al. Experimental on-demand recovery of entanglement by local operations within non-Markovian dynamics. Sci. Rep. 5, 1 (2015).
Valencia, N. H., Goel, S., McCutcheon, W., Defienne, H. & Malik, M. Unscrambling entanglement through a complex medium. Nat. Phys. 16, 1112 (2020).
Kim, Y. et al. Direct quantum process tomography via measuring sequential weak values of incompatible observables. Nat. Commun. 9, 1 (2018).
Kim, Y. et al. Universal compressive characterization of quantum dynamics. Phys. Rev. Lett. 124, 210401 (2020).
Emerson, J. et al. Symmetrized characterization of noisy quantum processes. Science 317, 1893 (2007).
Harper, R., Flammia, S. T. & Wallman, J. J. Efficient learning of quantum noise. Nat. Phys. 16, 1184 (2020).
Acknowledgements
This work was supported in part by the National Research Foundation of Korea (2019R1A2C3004812, 2020M3E4A1079939), the ITRC support program (IITP-2021-2020-0-01606), Agency for Defense Development (UG190028RD), the KIST institutional program (2E31021), the KIST Open Research Program, the QuantERA ERA-NET within the EU Horizon 2020 Programme, and the EPSRC (EP/R044082/1). M.S.K. acknowledges support from the KIAS visiting professorship and Samsung GRP grant.
Author information
Authors and Affiliations
Contributions
S.-W.L. and Y.-H.K. planned and supervised the research; D.-G.I. performed the experiment and analyzed the data; all authors contributed to analysis and discussion of the results; D.-G.I., S.-W.L., and Y.-H.K. wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Im, DG., Lee, CH., Kim, Y. et al. Optimal teleportation via noisy quantum channels without additional qubit resources. npj Quantum Inf 7, 86 (2021). https://doi.org/10.1038/s41534-021-00426-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00426-x
This article is cited by
-
The origin of improving the fidelity of the joint remote state preparation of an arbitrary qubit state affected by amplitude-damping noise
Quantum Information Processing (2023)
-
A review on quantum computing and deep learning algorithms and their applications
Soft Computing (2023)
-
Optimal tripartite quantum teleportation protocol through noisy channels
Quantum Information Processing (2023)
-
Quantum State Recovery Via Environment-assisted Measurement and Weak Measurement
International Journal of Theoretical Physics (2022)