Abstract
We study two-qubit circuits over the Clifford+CS gate set, which consists of the Clifford gates together with the controlled-phase gate CS = diag(1, 1, 1, i). The Clifford+CS gate set is universal for quantum computation and its elements can be implemented fault-tolerantly in most error-correcting schemes through magic state distillation. Since non-Clifford gates are typically more expensive to perform in a fault-tolerant manner, it is often desirable to construct circuits that use few CS gates. In the present paper, we introduce an efficient and optimal synthesis algorithm for two-qubit Clifford+CS operators. Our algorithm inputs a Clifford+CS operator U and outputs a Clifford+CS circuit for U, which uses the least possible number of CS gates. Because the algorithm is deterministic, the circuit it associates to a Clifford+CS operator can be viewed as a normal form for that operator. We give an explicit description of these normal forms and use this description to derive a worst-case lower bound of \(5{{\rm{log}}}_{2}(\frac{1}{\epsilon })+O(1)\) on the number of CS gates required to ϵ-approximate elements of SU(4). Our work leverages a wide variety of mathematical tools that may find further applications in the study of fault-tolerant quantum circuits.
Similar content being viewed by others
Introduction
In the context of fault-tolerant quantum computing, operations from the Clifford group are relatively easy to perform and are therefore considered inexpensive. In contrast, operations that do not belong to the Clifford group are complicated to execute fault-tolerantly because they require resource-intensive distillation protocols1. Since non-Clifford operations are necessary for universal quantum computing, it has become standard to use the number of non-Clifford gates in a circuit as a measure of its cost. This fault-tolerant perspective on the cost of circuits has profoundly impacted the field of quantum compiling and significant efforts have been devoted to minimizing the number of non-Clifford operations in circuits.
An important problem in quantum compiling is the problem of exact synthesis: given an operator U known to be exactly representable over some gate set G, find a circuit for U over G. An exact synthesis algorithm is a constructive solution to this problem. When the gate set G is an extension of the Clifford group, it is desirable that the exact synthesis algorithm for G be efficient and produce circuits that use as few non-Clifford gates as possible.
In the past few years, methods from algebraic number theory have been successfully applied to the exact synthesis problem associated to a variety of single-qubit2,3,4,5,6,7,8 and single-qutrit9,10,11,12 gate sets. In many cases, the resulting exact synthesis algorithms efficiently produce circuits that are optimal, in the sense that they use the least possible number of non-Clifford gates. These powerful exact synthesis methods were central in the development of good unitary approximation methods, which play a key role in the compilation of practical quantum programs2,3,7,8,13,14.
Exact synthesis algorithms also exist for various instantiations of the multi-qubit compiling problem, though each suffers shortcomings in some respect. Optimal algorithms for two-qubit circuits over continuous gate sets have been known for a number of years15,16. Unfortunately, such gate sets are not well-suited for fault-tolerant quantum computing. Multi-qubit exact synthesis algorithms for universal and fault-tolerant gate sets were introduced more recently17,18,19,20,21,22,23,24,25,26,27. Some of these algorithms, such as17,19,20,21,24,25,26, are proper synthesis algorithms: they input a unitary matrix and produce a circuit. Some other of these algorithms, such as18,22,23,27, are better referred to as re-synthesis algorithms: they input a circuit and produce an optimized circuit. Of course, a re-synthesis algorithm can be used in conjunction with a synthesis algorithm to obtain an alternative (and typically better) synthesis algorithm. While the algorithms of refs. 17,20 are far from optimal, the algorithms of19,21,24,26 synthesize provably optimal circuits by cleverly utilizing certain properties of fault-tolerant gate sets containing the Clifford group. However, the runtimes of these optimal synthesis algorithms are exponential in both qubit count and optimal circuit length. Powerful heuristics were introduced in26 achieving polynomial scaling with optimal circuit length. Unfortunately, even this improved heuristic algorithm takes thousands of seconds to compute optimal two-qubit circuits of practical size (40 non-Clifford operations) on modest hardware.
Not only are these multi-qubit exact synthesis algorithms impractical in many cases, they also fail to shed much light on the structure of optimal circuits. In the single-qubit case, intimate knowledge of this structure for certain gate sets was developed by describing optimal circuits via regular expressions or, equivalently, automata28. Such descriptions are of theoretical interest, but also have practical consequences. In particular, for certain single-qubit gate sets these descriptions allowed researchers to derive a rigorous lower-bound on the number of non-Clifford gates required to approximate typical elements of SU(2)29. Analogous statements about approximations of multi-qubit unitaries have eluded researchers thus far.
In the present paper, we introduce an efficient and optimal exact synthesis algorithm for a two-qubit gate set that is appropriate for universal and fault-tolerant quantum computing. We focus on two-qubit circuits over the Clifford+CS gate set, which consists of the Clifford gates together with the non-Clifford controlled-phase gate CS = diag(1, 1, 1, i). The CS gate has received recent attention as an alternative to the T-gate in methods for fault-tolerant quantum computing30,31 and due to its natural implementation as an entangling operation in certain superconducting qubit systems32,33,34,35 whose fidelity is approaching that of single-qubit gates36,37. Our algorithm produces an optimal circuit in a number of arithmetic operations linear in the length of the optimal decomposition. This is unlike existing multi-qubit synthesis methods. Moreover, because our algorithm is deterministic, the circuit it associates to a Clifford+CS operator can be viewed as a normal form for that operator. We give an explicit description of these normal forms in the language of automata and use this description to derive a worst-case lower bound of \(5{{\rm{log}}}_{2}(\frac{1}{\epsilon })+O(1)\) on the number of CS gates required to ϵ-approximate elements of SU(4). A Mathematica package implementing our algorithm is freely available online38. This code is very efficient, synthesizing optimal circuits of CS-count 10000 in 1.2 ± 0.1 s on modest hardware.
The paper is structured as follows. We first introduce a convenient set of generators in Section “Generators”. Then, in Section “The isomorphism SU(4) ≅ Spin(6)”, we describe the exceptional isomorphism SU(4) ≅ Spin(6). In Section “Exact synthesis”, we leverage this isomorphism to introduce an exact synthesis algorithm for Clifford+CS operators. In Sections “Automata as tools for describing normal forms” and “The structure of normal forms”, we use the theory of automata to study the structure of the circuits produced by the exact synthesis algorithm. We take advantage of this structure in Section “Lower bounds” to establish a worst-case lower bound on the number of non-Clifford resources required to ϵ-approximate elements of SU(4) using Clifford+CS circuits. Finally, we conclude and discuss avenues for future work in Section “Discussion”.
Results
Generators
Throughout, we use \({\mathbb{N}}\), \({\mathbb{Z}}\), \({\mathbb{R}}\), and \({\mathbb{C}}\) to denote the usual collection of numbers, \({{\mathbb{Z}}}_{p}\) to denote the collection integers modulo p, and \({\mathbb{Z}}\left[i\right]\) to denote the collection of Gaussian integers (the complex numbers with integer real and imaginary parts). We write ρ for the canonical homomorphism \({\mathbb{Z}}\to {{\mathbb{Z}}}_{2}\) (if \(n\in {\mathbb{Z}}\) then ρ(n) is the parity of n). For two integers n ≤ m, we write [n, m] for the set \(\left\{n,\ldots ,m\right\}\subseteq {\mathbb{Z}}\) and simply write [m] for [1, m]. We view scalars and vectors as matrices so that any concept defined for matrices of arbitrary dimensions also applies to scalars and vectors. Finally, for readability, we use the symbol ⋅ to denote the zero entries of a matrix.
The single-qubit Pauli gates X, Y, and Z are defined as
These gates generate the single-qubit Pauli group\(\left\{{i}^{a}P\,;\,a\in {{\mathbb{Z}}}_{4}\,\text{and}\,P\in \left\{I,X,Y,Z\right\}\right\}\). The two-qubit Pauli group, which we denote by \({\mathcal{P}}\), is defined as \({\mathcal{P}}=\left\{{i}^{a}(P\otimes \ Q)\,;\,a\in {{\mathbb{Z}}}_{4}\,\text{and}\,P,Q\in \left\{I,X,Y,Z\right\}\right\}\). The Clifford gates H, S, and CZ are defined as
These gates are known as the Hadamard gate, the phase gate, and the controlled-Z gate, respectively. The single-qubit Clifford group is generated by H and S and contains the primitive 8th root of unity \(\omega ={e}^{\frac{i\pi }{4}}\). The two-qubit Clifford group, which we denote by \({\mathcal{C}}\), consists of the operators which can be represented by a two-qubit circuit over the gate set \(\left\{H,S,{\rm{CZ}}\right\}\). Equivalently, \({\mathcal{C}}\) is generated by H ⊗ I, I ⊗ H, S ⊗ I, I ⊗ S, and CZ. Up to global phases, the Clifford groups are the normalizers of the Pauli groups.
Clifford gates are well-suited for fault-tolerant quantum computation but the Clifford group is not universal. One can obtain a universal group by extending \({\mathcal{C}}\) with the controlled-phase gate CS defined as
In what follows, we focus on the group \({\mathcal{G}}\) of operators which can be represented by a two-qubit circuit over the universal gate set \(\left\{H,S,{\rm{CZ}},{\rm{CS}}\right\}\). Equivalently, \({\mathcal{G}}\) is the group generated by H ⊗ I, I ⊗ H, S ⊗ I, I ⊗ S, CZ, and CS. We have \({\mathcal{P}}\subseteq {\mathcal{C}}\subseteq {\mathcal{G}}\). We sometimes refer to \({\mathcal{G}}\) as the Clifford + CS group or Clifford + controlled-phase group. We know from17 that \({\mathcal{G}}\) is the group of 4 × 4 unitary matrices of the form
where \(k\in {\mathbb{N}}\) and the entries of M belong to \({\mathbb{Z}}\left[i\right]\). In the fault-tolerant setting, the CS gate is considered vastly more expensive than any of the Clifford gates. As a result, the cost of a Clifford + CS circuit is determined by its CS-count: the number of CS gates that appear in the circuit. Our goal is to find circuits for the elements of \({\mathcal{G}}\) that are optimal in CS-count.
We start by introducing a generalization of the CS gate which will be helpful in describing the elements of \({\mathcal{G}}\).
Definition 2.1
Let P and Q be distinct elements of \({\mathcal{P}}\setminus \left\{I\right\}\) such that P and Q are Hermitian and PQ = QP. Then R(P, Q) is defined as
We have R(Z ⊗ I, I ⊗ Z) = CS. Moreover, since \({\mathcal{C}}\) normalizes \({\mathcal{P}}\) and CR(P, Q)C† = R(CPC†, CQC†) for every \(C\in {\mathcal{C}}\), we know that \(R(P,Q)\in {\mathcal{G}}\) for every appropriate \(P,Q\in {\mathcal{P}}\). We record some important properties of the R(P, Q) gates in the lemma below. Because the proof of the lemma is tedious but relatively straightforward, it is given in Supplementary Note 2.
Lemma 2.2
Let \(C\in {\mathcal{C}}\) and let P, Q, and L be distinct elements of \({\mathcal{P}}\setminus \left\{I\right\}\). Assume that P, Q, and L are Hermitian and that PQ = QP, PL = LP, and QL = − LQ. Then the following relations hold:
We will use the R(P, Q) gates of Definition 2.1 to define normal forms for the elements of \({\mathcal{G}}\). The equivalences given by Lemma 2.2 show that it is not necessary to use every R(P, Q) gate and the following definition specifies the ones we will be using.
Definition 2.3
Let \({{\mathcal{T}}}_{1}\) and \({{\mathcal{T}}}_{2}\) be the subsets of \({\mathcal{P}}\times {\mathcal{P}}\) given below.
The set \({\mathcal{S}}\) is defined as \({\mathcal{S}}=\left\{R(P,Q)\,;\,(P,Q)\in {{\mathcal{T}}}_{1}\,\text{or}\,(P,Q)\in {{\mathcal{T}}}_{2}\right\}\).
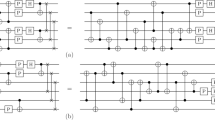
The set \({\mathcal{S}}\) contains 15 elements which are explicitly listed in Fig. 1. It can be verified that all of the elements of \({\mathcal{S}}\) are distinct, even up to right-multiplication by a Clifford gate. It will be helpful to consider the set \({\mathcal{S}}\) ordered as in Fig. 1, which is to be read left-to-right and row-by-row. We then write \({{\mathcal{S}}}_{j}\) to refer to the j-th element of \({\mathcal{S}}\). For example, \({{\mathcal{S}}}_{1}\) is in the top left of Fig. 1, \({{\mathcal{S}}}_{5}\) is in the top right, and \({{\mathcal{S}}}_{15}\) is in the bottom right. The position of R(P, Q) in this ordering roughly expresses the complexity of the Clifford circuit required to conjugate CS to R(P, Q).
These operators are one suitable choice for 15 \({\mathcal{R(P, Q)}}\) gates which are not equivalent to each other up to right-multiplication by Cliffords. All other choices are equivalent to this one up to right-multiplication by Cliffords. The ordering of \({\mathcal{S}}\) is given by reading left-to-right and row-by-row.
We close this section by showing that every element of \({\mathcal{G}}\) can be expressed as a sequence of elements of \({\mathcal{S}}\) followed by a single element of \({\mathcal{C}}\).
Lemma 2.4
Let P and Q be distinct elements of \({\mathcal{P}}\setminus \left\{I\right\}\) such that P and Q are Hermitian and PQ = QP. Then there exists \(P^{\prime} ,Q^{\prime} \in {\mathcal{P}}\) and \(C\in {\mathcal{C}}\) such that \(R(P^{\prime} ,Q^{\prime} )\in {\mathcal{S}}\) and \(R(P,Q)=R(P^{\prime} ,Q^{\prime} )C\).
Proof
Let P = ip(P1 ⊗ P2) and Q = iq(Q1 ⊗ Q2) with \({P}_{1},{P}_{2},{Q}_{1},{Q}_{2}\in \left\{I,X,Y,Z\right\}\). Since P and Q are Hermitian, p and q must be even. Moreover, by Eqs. (3) and (5) of Lemma 2.2, we can assume without loss of generality that p = q = 0 so that P = P1 ⊗ P2 and Q = Q1 ⊗ Q2. Now, if one of P1, P2, Q1, or Q2 is I, then we can use Eqs. (3), (4) and (5) of Lemma 2.2 to rewrite R(P, Q) as with \(C\in {\mathcal{C}}\) and \((P^{\prime} ,Q^{\prime} )\in {{\mathcal{T}}}_{1}\) as in Definition 2.3. If, instead, none of P1, P2, Q1, or Q2 are I, then we can reason similarly to rewrite R(P, Q) as \(R(P^{\prime} ,Q^{\prime} )C\) with \(C\in {\mathcal{C}}\) and \((P^{\prime} ,Q^{\prime} )\in {{\mathcal{T}}}_{2}\). □
Proposition 2.5
Let \(V\in {\mathcal{G}}\). Then V = R1 ⋯ RnC where \(C\in {\mathcal{C}}\) and \({R}_{j}\in {\mathcal{S}}\) for j ∊ [n].
Proof
Let \(V\in {\mathcal{G}}\). Then V can be written as V = C1 ⋅ CS ⋅ C2 ⋅ CS ⋅ … ⋅ Cn ⋅ CS ⋅ Cn+1 where \({C}_{j}\in {\mathcal{C}}\) for j ∊ [n + 1]. Since CS = R(Z ⊗ I, I ⊗ Z) we have
Now, by Eq. (2) of Lemma 2.2, \({C}_{1}R(Z\otimes \ I,I\otimes \ Z)={C}_{1}R(Z\otimes \ I,I\otimes \ Z){C}_{1}^{\dagger }{C}_{1}=R(P,Q){C}_{1}\) for some \(P,Q\in {\mathcal{P}}\). We can then apply Lemma 2.4 to get
with \(C^{\prime} =C{C}_{1}\in {\mathcal{C}}\) and \(R(P^{\prime} ,Q^{\prime} )\in {\mathcal{S}}\). Hence, setting \({R}_{1}=R(P^{\prime} ,Q^{\prime} )\) and \(C^{\prime} =C^{\prime} {C}_{2}\), Eq. (8) becomes
and we can proceed recursively to complete the proof.
The Isomorphism SU(4) ≅ Spin(6)
In this section, we describe the exceptional isomorphism SU(4) ≅ Spin(6) which will allow us to rewrite two-qubit operators as elements of SO(6). Consider some element U of SU(4). Then U acts on \({{\mathbb{C}}}^{4}\) by left-multiplication. Moreover, this action is norm-preserving. Now let \(\left\{{e}_{j}\right\}\) be the standard orthonormal basis of \({{\mathbb{C}}}^{4}\). From this basis, we construct an alternative six-component basis using the wedge product.
Definition 2.6
(Wedge product). Let a ∧ b be defined as the wedge product of a and b. Wedge products have the following properties given vectors \(a,b,c\in {{\mathbb{C}}}^{n}\) and \(\alpha ,\beta \in {\mathbb{C}}\):
-
Anticommutativity: a ∧ b = − b ∧ a.
-
Associativity: (a ∧ b) ∧ c = a ∧ (b ∧ c).
-
Bilinearity: (αa + βb) ∧ c = α(a ∧ c) + β(b ∧ c).
Note that the anticommutation of wedge products implies that a ∧ a = 0. We say that \({v}_{1}\wedge \ \cdots \wedge \ {v}_{k}{\in \bigwedge }^{k}{{\mathbb{C}}}^{n}\) for \({v}_{j}\in {{\mathbb{C}}}^{n}\). To compute the inner product of two wedge products v1 ∧ ⋯ ∧ vk and w1 ∧ ⋯ ∧ wk, we compute
where 〈vq, wr〉 is the entry in the q-th row and r-th column of a k × k matrix.
Remark 2.7
The magnitude of a wedge product of n vectors can be thought of as the n dimensional volume of the parallelotope constructed from those vectors. The orientation of the wedge product defines the direction of circulation around that parallelotope by those vectors.
The wedge product of two vectors in \({{\mathbb{C}}}^{4}\) can be decomposed into a six-component basis as anticommutativity reduces the 16 potential wedge products of elements of \(\left\{{e}_{j}\right\}\) to six. We choose this basis as
where
We note that B is an orthonormal basis and we assume that B is ordered as in Eq. (9).
Definition 2.8
Let U ∊ SU(4) and \(\overline{U}\) be its representation in the transformed basis. Let \(v,w\in {{\mathbb{C}}}^{4}\) with \(v\wedge \ w{\in \bigwedge }^{2}{{\mathbb{C}}}^{4}\). Then the actions of U and \(\overline{U}\) are related by
To avoid confusion, we use an overline, as in \(\overline{O}\), to denote the SO(6) representation of an operator or set of operators O. We are now equipped to define the transformation from SU(4) to SO(6).
Definition 2.9
Let U ∊ SU(4) and let j, k ∊ [6]. Then the entry in the j-th row and k-th column of the SO(6) representation \(\overline{U}\) of U is
where Bj is the jth element in the ordered basis B, the action of \(\overline{U}\) on Bk is defined by Definitions 2.6 and 2.8, and the inner product is defined by Definitions 2.6.
As an illustration of the process specified in Definition 2.9, we explicitly calculate the SO(6) representation of a Clifford+CS operator in Supplementary Note 1. Moreover, we provide code to compute this isomorphism for any input with our Mathematica package38.
Remark 2.10
The fact that this isomorphism yields special orthogonal operators is ultimately due to the fact that the Dynkin diagrams for the Lie algebras of SU(4), Spin(6), and SO(6) are equivalent. However, this fact can be easily illustrated through the Euler decomposition of SU(4)39. Direct calculation of \(\overline{U}\) for the operator
for ∣α∣ = 1 and α = r + ic with \(r,c\in {\mathbb{R}}\) yields
which is explicitly in SO(6). Computation of the other 14 Euler angle rotations required for an SU(4) parameterization yields similar matrices, likewise in SO(6). Since SO(6) is a group under multiplication, the isomorphism applied to any U ∊ SU(4) yields \(\overline{U}\in {\rm{SO}}(6)\).
We close this section by explicitly calculating the SO(6) representation of each of the generators of \({\mathcal{G}}\). We multiply the generators by overall phase factors to ensure that each operator has determinant one, and furthermore that single-qubit operators have determinant one on their single-qubit subspace. Later, when referring to gates or their SO(6) representation, we omit overall phases for readability.
Proposition 2.11
The image of the generators of \({\mathcal{C}}\) in SO(6) are
Proposition 2.12
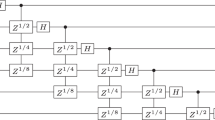
The elements of \(\overline{{\mathcal{S}}}\) are given in Fig. 2.
Exact synthesis
In this section, we leverage the isomorphism SU(4) ≅ Spin(6) described in the previous section to find optimal decompositions for the elements of \({\mathcal{G}}\). We will be working extensively with the matrix group
Note that \({\mathcal{H}}\subseteq {\rm{SO}}(6)\). Our interest in \({\mathcal{H}}\) stems from the following observation.
Proposition 2.13
We have \(\overline{{\mathcal{G}}}\subseteq {\mathcal{H}}\).
Proof
The property holds for the generators of \(\overline{{\mathcal{G}}}\) by Propositions 2.11 and 2.12. □
In the remainder of this section, we prove the converse of Proposition 2.13 by defining an algorithm which inputs an element of \({\mathcal{H}}\) and outputs a product of generators. We start by introducing a few notions that are useful in discussing the elements of \({\mathcal{H}}\).
Definition 2.14
Let \(V\in {\mathcal{H}}\). We say that \(\ell \in {\mathbb{N}}\) is a denominator exponent of V if \({\sqrt{2}}^{\ell }V\in {{\mathbb{Z}}}^{6\times 6}\). The least such ℓ is the least denominator exponent of V, which we denote by lde(V).
Lemma 2.15
Let \(U\in {\mathcal{G}}\) and suppose that \({\mathrm{lde}}\,(\overline{U})=k\). Then any Clifford+CS circuit for U has CS-count at least k.
Proof
The only generators with a factor of \(1/\sqrt{2}\) in their SO(6) representation are the elements of \({\mathcal{S}}\). Thus, for a least denominator exponent of k there must be at least k of these operators, each of which requires a single CS gate. □
Definition 2.16
Let \(V\in {\mathcal{H}}\) and let ℓ be a denominator exponent of V. The ℓ-residue of V is the binary matrix \({\rho }_{\ell }(V)\in {{\mathbb{Z}}}_{2}^{6\times 6}\) defined by
where \(\rho :{\mathbb{Z}}\to {{\mathbb{Z}}}_{2}\) is the canonical (parity) homomorphism.
The residue matrices introduced in Definition 2.16 are important in the definition of the exact synthesis algorithm. Indeed, the ℓ-residue of a Clifford+CS operator U determines the element of \({\mathcal{S}}\) to use in order to reduce the least denominator exponent of U (although not uniquely, as we discuss below). Similar residue matrices are used in the study of other fault-tolerant circuits17,28.
Recall that if A is a set, then a partition of A is a collection of disjoint nonempty subsets of A whose union is equal to A. The set of all partitions of a set A is denoted \({{\mathscr{B}}}_{A}\). Let p and \(p^{\prime}\) be two partitions of A. If every element of p is a subset of an element of \(p^{\prime}\) then we say that \(p^{\prime}\) is coarser than p and that p is finer than \(p^{\prime}\).
Definition 2.17
Let \(N\in {{\mathbb{Z}}}_{2}^{6\times 6}\) be a binary matrix with rows r1, …, r6 and let \(p=\left\{{p}_{1},\ldots ,{p}_{q}\right\}\) be a partition of the set [6]. Then N has the patternp if for any pj in p and any j1, j2 ∊ pj we have \({r}_{{j}_{1}}={r}_{{j}_{2}}\). In this case we also say that N has a ∣p1∣ × … × ∣pq∣ pattern.
Definition 2.18
Let \(V\in {\mathcal{H}}\) with lde(V) = ℓ. We define the pattern map \({\mathfrak{p}}:{\mathcal{H}}\to {{\mathscr{B}}}_{[6]}\) as the function which maps V to the pattern of ρℓ(V). We say that \(p={\mathfrak{p}}(V)\) is the pattern of V. If V1 and V2 are two elements of \({\mathcal{H}}\), we say that V1 is finer than V2 or that V2 is coarser than V1 if these statements hold for \({\mathfrak{p}}({V}_{1})\) and \({\mathfrak{p}}({V}_{2})\).
Remark 2.19
In a slight abuse of notation, we extend the pattern map to any valid representation of a Clifford+CS operator. Given a Clifford+CS operator with SU(4) representation U which can be written as a word W over the generators and with SO(6) representation \(\overline{U}\), we set \({\mathfrak{p}}(U)={\mathfrak{p}}(W)={\mathfrak{p}}(\overline{U})\). This extension is unambiguous after fixing our transformation from SU(4) to SO(6), as \({\mathfrak{p}}\) is insensitive to relative phase changes in U. We incorporate all relational notions described in Definition 2.18 in this extension.
We now analyze the image in SO(6) of certain subsets of \({\mathcal{G}}\). We start by showing that the image of the Clifford group \({\mathcal{C}}\) is exactly the collection of elements of \({\mathcal{H}}\) with least denominator 0. In other words, \(\overline{{\mathcal{C}}}\) is the group of 6-dimensional signed permutation matrices.
Lemma 2.20
Let \(V\in {\mathcal{H}}\). Then lde(V) = 0 if and only if \(V\in \overline{{\mathcal{C}}}\).
Proof
The least denominator exponent of \(\overline{H\otimes \ I}\), \(\overline{I\otimes \ H}\), \(\overline{S\otimes \ I}\), \(\overline{I\otimes \ S}\), and \(\overline{{\rm{CZ}}}\) is 0. Thus, if \(U\in {\mathcal{C}}\) then \({\mathrm{lde}}\,(\overline{U})=0\). For the converse, let C1 and C2 be the Clifford operators (ω†S) ⊗ I and (H ⊗ H)(ω†CZ)(Z ⊗ Z), respectively. Then
The operators \(\overline{{C}_{1}}\) and \(\overline{{C}_{2}}\) generate \(\left\{V\in {\mathcal{H}}\,;\,{\mathrm{lde}}\,(V)=0\right\}\). Hence, if \(V\in {\mathcal{H}}\) and lde(V) = 0 then V can be expressed as a product of the image of Clifford gates. □
Lemma 2.21
Let \(V\in {\mathcal{H}}\). Then lde(V) = 1 if and only if \(V=\overline{RC}\) for some \(R\in {\mathcal{S}}\) and some \(C\in {\mathcal{C}}\). Furthermore, V has a 2 × 2 × 2 pattern.
Proof
The rows of V have unit norm and are pairwise orthogonal. Hence, up to a signed permutation of rows and columns, there is only one such matrix, e.g.,
By Proposition 2.5 the proof is complete, since Clifford operators correspond to signed permutations by Lemma 2.20. □
Lemma 2.22
Let \(V\in {\mathcal{H}}\) with lde(V) = k ≥ 2. Then V has either a 2 × 2 × 2 or 2 × 4 pattern.
Proof
Let \(V\in {\mathcal{H}}\). Since V is orthogonal, we have V†V = I. Hence, \({({\sqrt{2}}^{k}V)}^{\dagger }({\sqrt{2}}^{k}V)={2}^{k}I\). Since k ≥ 2, this implies that the inner product of any column of \({\sqrt{2}}^{k}V\) with itself is congruent to 0 modulo 4. Similarly, the inner product of two distinct columns \({\sqrt{2}}^{k}V\) is congruent to 0 modulo 4. Letting, M = ρk(V), we then have the column relations
as well as analogous row relations. For \(x\in {\mathbb{Z}}\), \({x}^{2}=0\,{\mathrm{mod}}\,\,4\) if and only if \(x=0\,{\mathrm{mod}}\,\,2\). Hence, there must be exactly zero or four odd entries in every column (or row) of M by Eq. (14). By Eq. (15), we see that the inner product of any two distinct rows must be even. Up to a permutation of rows and columns, we can then deduce that M is one of the two matrices below, which completes the proof.
□
Corollary 2.23
Let \(V\in {\mathcal{H}}\) with lde(V) = k ≥ 1. Then V has either a 2 × 2 × 2 or 2 × 4 pattern.
Lemma 2.24
Let \(V\in {\mathcal{H}}\) and assume that lde(V) = k ≥ 1. If \(\overline{R}\in \overline{{\mathcal{S}}}\) is finer than V, then \({\mathrm{lde}}\,({\overline{R}}^{{\mathsf{T}}}V)=k-1\).
Proof
For simplicity, we assume that \({\mathfrak{p}}(\overline{R})=\left\{\left\{1,2\right\},\left\{3,4\right\},\left\{5,6\right\}\right\}\). The cases in which \({\mathfrak{p}}(\overline{R})\) is another pattern are treated similarly. For j ∊ [6], let rj denote the rows of \({\sqrt{2}}^{k}V\). Since \({\mathfrak{p}}(V)\) is coarser than \({\mathfrak{p}}(\overline{R})\), we have r1 ≡ r2, r3 ≡ r4, r5 ≡ r6 modulo 2. This implies that r1 ± r2 ≡ r3 ± r4 ≡ r5 ± r6 ≡ 0 modulo 2. Hence
where each \(r^{\prime}\) is a vector of integers. □
Lemma 2.25
Let \(V\in {\mathcal{H}}\) with lde(V) ≥ 1. Then there exists \(R\in {\mathcal{S}}\) such that \({\mathrm{lde}}\,({\overline{R}}^{{\mathsf{T}}}V)={\mathrm{lde}}\,(V)-1\).
Proof
By inspection of Fig. 2 we see that for every 2 × 2 × 2 pattern q there exists \(R\in {\mathcal{S}}\) such that \({\mathfrak{p}}(\overline{R})=q\). As a result, if \({\mathfrak{p}}(V)\) is a 2 × 2 × 2 or a 2 × 4 pattern, then there exists \(R\in {\mathcal{S}}\) such that \(\overline{R}\) has a pattern finer than \({\mathfrak{p}}(V)\). By Corollary 2.23, \({\mathfrak{p}}(V)\) is in fact a 2 × 2 × 2 row-pattern or a 2 × 4 row-pattern and thus there exists \(R\in {\mathcal{S}}\) such that \(\overline{R}\) is finer than V. We can then conclude by Lemma 2.24. □
Theorem 2.26
We have \(\overline{{\mathcal{G}}}={\mathcal{H}}\).
Proof
\(\overline{{\mathcal{G}}}\subseteq {\mathcal{H}}\) by Proposition 2.13. We now show \({\mathcal{H}}\subseteq \overline{{\mathcal{G}}}\). Let \(V\in {\mathcal{H}}\). We proceed by induction on the least denominator exponent of V. If lde(V) = 0 then, by Lemma 2.20, \(V\in \overline{{\mathcal{C}}}\) and therefore \(V\in \overline{{\mathcal{G}}}\). Now if lde(V) > 0, let R be the element of \({\mathcal{S}}\) with the lowest index such that \({\mathrm{lde}}\,({\overline{R}}^{{\mathsf{T}}}V)=k-1\). Such an element exists by Lemma 2.25. By the induction hypothesis we have \({\overline{R}}^{{\mathsf{T}}}V\in \overline{{\mathcal{G}}}\) which implies that \(\overline{R}({\overline{R}}^{{\mathsf{T}}}V)=V\in \overline{{\mathcal{G}}}\). □
The proof of Theorem 2.26 provides an algorithm to decompose an arbitrary element of \(\overline{{\mathcal{G}}}\) into a product of elements of \(\overline{{\mathcal{S}}}\), followed by an element of \(\overline{{\mathcal{C}}}\). In the proof, there is freedom in choosing the element of \(\overline{{\mathcal{S}}}\) used to reduce \({\mathrm{lde}}\,(\overline{V})\). If there is more than one generator with a finer pattern than \(\overline{V}\), we must make a choice. The ordering imposed on \({\mathcal{S}}\) in Section “Generators” is used to make this choice in a uniform manner: we always choose the element of \({\mathcal{S}}\) of lowest index. As a result, the exact synthesis algorithm becomes deterministic. The ambiguity in the choice of generator is a consequence of the relations given in Lemma 2.2. In particular, we have
and these three distinct sequences of generators denote the same operator. This is the source of the three-fold ambiguity in choosing a finer 2 × 2 × 2 pattern for a given 2 × 4 pattern.
We will sometimes refer to the association between elements of \({\mathcal{S}}\) and patterns used in the exact synthesis algorithm of Theorem 2.26 as the first finer partition association, or FFP for short. The association is explicitly described Table 1.
Theorem 2.27
If U is a Clifford+CS operator such that \({\mathrm{lde}}\,(\overline{U})=k\), then U can be represented by a Clifford+CS circuit of CS-count k. This circuit is optimal in CS-count and can be constructed in \({\mathcal{O}}(k)\) arithmetic operations.
Proof
Let U be as stated. If k = 0, then \(\overline{U}\) belongs to \(\overline{C}\) and U is therefore a Clifford. If k > 0, then as in Theorem 2.26, there is a unique \({R}_{k}\in {\mathcal{S}}\) given by FFP such that \({\mathrm{lde}}\,({\overline{R}}_{k}^{{\mathsf{T}}}\overline{U})=k-1\). By induction on the least denominator exponent, we have a deterministic synthesis algorithm to find a sequence such that
which then implies that U = Rk ⋯ R1C. Each of these k steps involves a constant number of basic arithmetic operations. This circuit has CS-count k, which is optimal by Lemma 2.15. □
Our Mathematica package38 implements the algorithm referred to in Theorem 2.27 as well as a significant amount of other tools for two-qubit Clifford + CS circuits. Testing of the performance of this algorithm on a modest device is presented in Table 2.
Automata as tools for describing normal forms
In the previous section, we introduced a synthesis algorithm for Clifford+CS operators. The algorithm takes as input a Clifford+CS matrix and outputs a circuit for the corresponding operator. The circuit produced by the synthesis algorithm is a word over the alphabet \({\mathcal{S}}\cup {\mathcal{C}}\). Because the algorithm is deterministic, the word it associates to each operator can be viewed as a normal form for that operator. In the present section, we use the language of automata to give a detailed description of the structure of these normal forms. We include the definitions of some basic concepts from the theory of automata for completeness. The reader looking for further details is encouraged to consult40.
In what follows we sometimes refer to a finite set Σ as an alphabet. In such a context, the elements of Σ are referred to as letters, Σ* denotes the set of words over Σ (which includes the empty word ε), and the subsets of Σ* are called languages over Σ. If w ∊ Σ* is a@@ word over the alphabet Σ, we write ∣w∣ for the length of w. Finally, if L and \(L^{\prime}\) are two languages over an alphabet Σ then their concatenation\(L\circ L^{\prime}\) is defined as \(L\circ L^{\prime} =\left\{ww^{\prime} \,;\,w\in L\,\text{and}\,w^{\prime} \in L^{\prime} \right\}\).
Definition 2.28
A nondeterministic finite automaton is a 5-tuple (Σ, Q, In, Fin, δ) where Σ and Q are finite sets, In and Fin are subsets of Q, and \(\delta :Q\times ({{\Sigma }}\cup \left\{\varepsilon \right\}):\to {\mathscr{P}}(Q)\) is a function whose codomain is the power set of Q. We call Σ the alphabet, Q the set of states, In and Fin the sets of initial and final states, and δ the transition function.
Remark 2.19
definition 2.28 is slightly non-standard. indeed, automata are typically defined as having a single initial state, rather than a collection of them. one can then think of definition 2.28 as introducing a collection of automata: one for each element of In. Alternatively, definition 2.28 can also be recovered from the usual definition by assuming that every automaton in the sense of definition 2.28 in fact has a single initial state s0 related to the elements of In by δ(s0, ε) = In. we chose to introduce automata as in definition 2.28 because this results in a slightly cleaner presentation.
It is common to define an automaton A = (Σ, Q, In, Fin, δ) by specifying a directed labeled graph called the state graph of A. The vertices of the graph are labeled by states and there is an edge labeled by a letter w ∊ Σ between vertices labeled q and \(q^{\prime}\) if \(q^{\prime} \in \delta (q,w)\). The initial and final states are distinguished using arrows and double lines, respectively. For brevity, parallel edges are drawn only once, with their labels separated by a comma.
Example 2.30
The state graph for a nondeterministic finite automaton A = (Σ, Q, δ, In, Fin) is depicted below.

Here, \(Q=\left\{{q}_{0},{q}_{1},{q}_{2},{q}_{3}\right\}\), \({{\Sigma }}=\left\{0,1\right\}\), the collection of initial states is \({\mathrm{In}}\,=\left\{{q}_{0}\right\}\), the collection of final states is \({\mathrm{Fin}}\,=\left\{{q}_{3}\right\}\), and we have, e.g., \(\delta ({q}_{0},1)=\left\{{q}_{0},{q}_{1}\right\}\).
An automaton A = (Σ, Q, In, Fin, δ) can be used to specify a language \({\mathcal{L}}(A)\subseteq {{{\Sigma }}}^{* }\). Intuitively, \({\mathcal{L}}(A)\) is the collection of all the words over Σ that specify a well-formed walk along the state graph of A. The following definition makes this intuition more precise.
Definition 2.31
Let A = (Σ, Q, In, Fin, δ) be an automaton. Then Aaccepts a word w = w1 ⋯ wm ∊ Σ* if there exists a sequence of states s0, s1, …, sm ∊ Q such that
-
1.
s0 ∊In,
-
2.
sj+1 ∊δ(si, wj+1) for \(j\in \left\{0,\ldots ,m-1\right\}\), and
-
3.
sm ∊ Fin.
The set of words accepted by A is called the language recognized by A and is denoted \({\mathcal{L}}(A)\).
Example 2.32 The alphabet for the automaton A given in Example 2.30 is \({{\Sigma }}=\left\{0,1\right\}\). The language recognized by A is \({\mathcal{L}}(A)=\left\{w\in {{{\Sigma }}}^{* }\,;\,\,\text{the third rightmost letter of}\,\ w\ \,\text{is 1}\,\right\}\).
If a language is recognized by some nondeterministic finite automata then that language is called regular. The collection of regular languages is closed under a variety of operations. In particular, regular languages are closed under concatenation.
Definition 2.33
Let A = (Σ, Q, In, Fin, δ) and \(A^{\prime} =({{\Sigma }},Q^{\prime} ,{\mathrm{In}}\,^{\prime} ,{\mathrm{Fin}}\,^{\prime} ,\delta ^{\prime} )\) be two automata. Then the concatenation of A and \(A^{\prime}\) is the automaton \(A\circ A^{\prime} =({{\Sigma }},Q^{\prime\prime} ,{\mathrm{In}}\,,{\mathrm{Fin}}\,^{\prime} ,\delta ^{\prime\prime} )\) where \(Q^{\prime\prime} =Q\sqcup Q^{\prime}\) is the disjoint union of Q and \(Q^{\prime}\) and
Proposition 2.34
Let A and \(A^{\prime}\) be automata recognizing languages L and \(L^{\prime}\), respectively. Then \(A\circ A^{\prime}\) recognizes \(L\circ L^{\prime}\).
An example of the concatenation of two automata is provided in Fig. 3 and Example 2.38 based off of the automata defined in Definitions 2.36 and 2.37 below.
The set of states of this automaton is \(\left\{1,2,3,0^{\prime} ,1^{\prime} ,\ldots ,k^{\prime} \right\}\), which is the disjoint union of the states \(\left\{1,2,3\right\}\) of \({{\mathfrak{S}}}_{1,3}\) and the states \(\left\{0,1,\ldots ,k\right\}\) of \({\mathfrak{C}}\). The initial states are \(\left\{1,2,3\right\}\), those of \({{\mathfrak{S}}}_{1,3}\), and the final states are \(\left\{1^{\prime} ,\ldots ,k^{\prime} \right\}\), those of \({\mathfrak{C}}\). Because \({{\mathfrak{S}}}_{1,3}\) has \({\mathrm{Fin}}\,=\left\{1,2,3\right\}\) and \({\mathfrak{C}}\) has \({\mathrm{In}}\,=\left\{0^{\prime} \right\}\), the transition function δ of \({{\mathfrak{S}}}_{1,3}\circ {\mathfrak{C}}\) is such that \(\delta (1,\varepsilon )=\delta (2,\varepsilon )=\delta (3,\varepsilon )=\left\{0^{\prime} \right\}\). Otherwise, δ behaves like the transition function for \({{\mathfrak{S}}}_{1,3}\) on the subset of states \(\left\{1,2,3\right\}\) and like the transition function for \({\mathfrak{C}}\) on the subset of states \(\left\{0^{\prime} ,1^{\prime} ,\ldots ,k^{\prime} \right\}\).
The structure of normal forms
We now consider the alphabet \({\mathcal{S}}\cup {\mathcal{C}}\) and describe the words over \({\mathcal{S}}\cup {\mathcal{C}}\) that are output by the synthesis algorithm of Theorem 2.27.
Definition 2.35
Let \(U\in {\mathcal{G}}\). The normal form of U is the unique word over \({\mathcal{S}}\cup {\mathcal{C}}\) output by the synthesis algorithm of Theorem 2.27 on input U. We write \({\mathcal{N}}\) for the collection of all normal forms.
To describe the elements of \({\mathcal{N}}\), we introduce several automata. It will be convenient for our purposes to enumerate the elements of \({\mathcal{C}}\). We therefore assume that a total ordering of the 92160 elements of \({\mathcal{C}}\) is chosen and we write \({{\mathcal{C}}}_{j}\) for the j-th element of \({\mathcal{C}}\).
Definition 2.36
Let \(k=| {\mathcal{C}}|\) and \({{\Sigma }}={\mathcal{S}}\cup {\mathcal{C}}\). The automaton \({\mathfrak{C}}\) is defined as \({\mathfrak{C}}=({{\Sigma }},[0,k],\left\{0\right\},[k],{\delta }_{{\mathfrak{C}}})\) where, for s ∊ [0, k] and ℓ ∊ Σ, we have
Definition 2.37
Let \({{\Sigma }}={\mathcal{S}}\cup {\mathcal{C}}\). The automaton \({{\mathfrak{S}}}_{n,m}\) is defined as \({{\mathfrak{S}}}_{n,m}=({{\Sigma }},[m],[n,m],[m],{\delta }_{{\mathfrak{S}},m})\) where, for s ∊ [m] and ℓ ∊ Σ, we have
Example 2.38. To illustrate Defiitions 2.33, 2.36, and 2.37, the automaton \({{\mathfrak{S}}}_{1,3}\circ {\mathfrak{C}}\) is represented in Fig. 3. It can be verified that the words \({{\mathcal{C}}}_{2}\), \({{\mathcal{S}}}_{2}{{\mathcal{S}}}_{1}{{\mathcal{C}}}_{1}\), and \({{\mathcal{S}}}_{3}{{\mathcal{S}}}_{1}{{\mathcal{S}}}_{2}{{\mathcal{C}}}_{k}\) are accepted by \({{\mathfrak{S}}}_{1,3}\circ {\mathfrak{C}}\) while the words \({{\mathcal{S}}}_{1}{{\mathcal{S}}}_{1}{{\mathcal{C}}}_{4}\) and \({{\mathcal{S}}}_{3}{{\mathcal{C}}}_{7}{{\mathcal{S}}}_{1}\) are not. Note in particular that if \({{\mathcal{C}}}_{1}\) is the symbol for the identity, then \({{\mathcal{S}}}_{3}{{\mathcal{C}}}_{1}\) is distinct (as a word) from \({{\mathcal{S}}}_{3}\). The former is accepted by \({{\mathfrak{S}}}_{1,3}\circ {\mathfrak{C}}\) while the latter is not. Despite the state graph of \({{\mathfrak{S}}}_{1,3}\) being fully-connected, full-connectivity does not necessarily hold for state graphs of other \({{\mathfrak{S}}}_{n,m}\) automata.
We will use the automata introduced in Definitions 2.36 and 2.37 to describe the elements of \({\mathcal{N}}\). Our goal is to show that
We start by establishing a few propositions.
Proposition 2.39
We have \({\mathcal{L}}({\mathfrak{C}})\subsetneq {\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\subsetneq {\mathcal{L}}({{\mathfrak{S}}}_{1,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\subsetneq {\mathcal{L}}({{\mathfrak{S}}}_{1,3}\circ {{\mathfrak{S}}}_{4,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\), where ⊊ denotes strict inclusion.
Proof
By Definitions 2.36 and 2.37. □
We emphasize that the inclusions in Proposition 2.39 are strict. This implies that \({\mathcal{L}}({{\mathfrak{S}}}_{1,3}\circ {{\mathfrak{S}}}_{4,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\) can be written as the disjoint union of \({\mathcal{L}}({\mathfrak{C}})\), \({\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\), and \({\mathcal{L}}({{\mathfrak{S}}}_{1,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\). The lemmas below show that these languages correspond to disjoint subsets of \({\mathcal{N}}\) and, in combination, suffice to prove Eq. (17).
Lemma 2.40
Let U be a word over \({\mathcal{S}}\cup {\mathcal{C}}\). Then \(U\in {\mathcal{L}}({\mathfrak{C}})\) if and only if \(U\in {\mathcal{N}}\) and U has length 1, i.e, \(U\in {\mathcal{C}}\).
Proof
By Definition 2.36 and Theorem 2.27. □
Lemma 2.41
Let U be a word over \({\mathcal{S}}\cup {\mathcal{C}}\). Then \(U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\setminus {\mathcal{L}}({\mathfrak{C}})\) if and only if \(U\in {\mathcal{N}}\) and U has a 2 × 2 × 2 pattern.
Proof
First, note that \({\mathcal{L}}({\mathfrak{C}})\) is the set of words of length 1 accepted by \({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}}\). This means that \({\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\setminus {\mathcal{L}}({\mathfrak{C}})\) consists of all the words of length k ≥ 2 accepted by \({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}}\). Furthermore, by Lemma 2.20, there are no normal forms of length 1 which have a 2 × 2 × 2 pattern. Thus, to prove our lemma it suffices to establish the following equality of sets
for all k ≥ 2. We proceed by induction on k.
-
Note that, by definition of \({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}}\), we have \(\left\{U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\,;\,| U| =2\right\}={\mathcal{S}}{\mathcal{C}}\). Every element of \({\mathcal{S}}{\mathcal{C}}\) has a 2 × 2 × 2 pattern by Lemma 2.21. Moreover, for U = SC with \(S\in {\mathcal{S}}\) and \(C\in {\mathcal{C}}\), \({\mathfrak{p}}(SC)={\mathfrak{p}}(S)\). Thus, SC must also be the unique word produced by the synthesis algorithm on input U and hence \(U\in {\mathcal{N}}\). This accounts for all words of length 2 in \({\mathcal{N}}\). Therefore Eq. (18) holds when k = 2.
-
Now suppose that Eq. (18) holds for some k ≥ 2. Let \(U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\) be a word of length k whose first letter is \(S\in {\mathcal{S}}\). Then \(U\in {\mathcal{N}}\) and \({\mathfrak{p}}(U)={\mathfrak{p}}(S)\) is a 2 × 2 × 2 pattern. Furthermore, the least denominator exponent of \(\overline{U}\) is k − 1. We will show that Eq. (18) holds for k + 1 by establishing two inclusions. Because it will sometimes be convenient to refer to submatrices, if M is an n × n matrix and x, y ⊆ [n], we write
$$M[x;y]$$for the submatrix of M formed from the rows with index in x and the columns with index in y.
⊆: Suppose that \(U^{\prime} =S^{\prime} U\) is a word of length k + 1 accepted by \({\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\). Then by Definition 2.37 we have \({\mathfrak{p}}(S^{\prime} )\cap {\mathfrak{p}}(S)=\varnothing\). Let \(\left\{a,b\right\}\in {\mathfrak{p}}(S^{\prime} )\), and let ra and rb be the corresponding rows of the residue matrix of \(\overline{U}\). Explicitly, we have
with ra ≠ rb as \(\left\{a,b\right\}\) is not a subset of any element of \({\mathfrak{p}}(U)\). Direct calculation of the rows of the residue matrix for \(\overline{U}^{\prime}\) yields
We conclude that \(\left\{a,b\right\}\) is a subset of an element of \({\mathfrak{p}}(U^{\prime} )\). Furthermore, by Lemma 2.22 and Eq. (16) we see that, since ra + rb ≠ 0, \({\mathfrak{p}}(U^{\prime} )\) cannot be a 2 × 4 pattern, and therefore \(\left\{a,b\right\}\in {\mathfrak{p}}(U^{\prime} )\). As this holds for all \(\left\{a,b\right\}\in {\mathfrak{p}}(S^{\prime} )\), we conclude that \({\mathfrak{p}}(S^{\prime} )={\mathfrak{p}}(U^{\prime} )\). Thus, by the induction hypothesis, \(S^{\prime} U\) will be the word produced by the synthesis algorithm when applied to \(U^{\prime}\). Hence, \(U^{\prime} \in {\mathcal{N}}\) and \({\mathfrak{p}}(U^{\prime} )\) is a 2 × 2 × 2 pattern.
⊇ : Suppose that \(U^{\prime}\) is a normal form of length k + 1 with a 2 × 2 × 2 pattern. Write \(U^{\prime}\) as \(U^{\prime} =S^{\prime} V\) for some unknown normal form V. We then have \({\mathfrak{p}}(S^{\prime} )={\mathfrak{p}}(U^{\prime} )\). Let \(\left\{a,b\right\}\in {\mathfrak{p}}(S^{\prime} )\) and let the corresponding rows of the residue matrix of \(\overline{V}\) be ra and rb. Explicitly, we have
Direct calculation of the rows of the residue matrix for \(\overline{U}^{\prime}\) yields
Since \({\mathfrak{p}}(U^{\prime} )\) is not a 2 × 4 pattern, we conclude that ra + rb ≠ 0 and thus that ra ≠ rb. Therefore, there is no element of cardinality four in \({\mathfrak{p}}(V)\). Since lde(V) > 0, \({\mathfrak{p}}(V)\) must then be a 2 × 2 × 2 pattern. Consequently, we have V = U as defined above. Because \(\left\{a,b\right\}\,\notin \,{\mathfrak{p}}(U)={\mathfrak{p}}(S)\), we know \({\mathfrak{p}}(S^{\prime} )\cap {\mathfrak{p}}(S)=\varnothing\). Given that \(S^{\prime} ={{\mathcal{S}}}_{j^{\prime} }\) and \(S={{\mathcal{S}}}_{j}\), we conclude that \(j\in {\delta }_{{\mathfrak{S}},15}(j^{\prime} ,S^{\prime} ={{\mathcal{S}}}_{j^{\prime} })\). Because \(S={{\mathcal{S}}}_{j}\) is the first letter of the word U, we know the initial state of U must be j. Therefore, by the induction hypothesis, \(U^{\prime} =S^{\prime} U\) is accepted by \({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}}\).
We have shown that Eq. (18) holds for words of length k + 1 if it holds for words of length k. This completes the inductive step. □
Lemma 2.41 characterized the normal forms that have a 2 × 2 × 2 pattern. The two lemmas below jointly characterize the normal forms that have a 2 × 4 pattern. Because their proofs are similar in spirit to that of Lemma 2.41, they have been relegated to Supplementary Note 3.
Lemma 2.42
Let U be a word over \({\mathcal{S}}\cup {\mathcal{C}}\). Then \(U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\setminus {\mathcal{L}}({{\mathfrak{S}}}_{1,15}\circ {\mathfrak{C}})\) if and only if \(U\in {\mathcal{N}}\) and U has a 2 × 4 pattern with \({\mathfrak{p}}(U)\cap \left\{\left\{x,y\right\}\,;\,(x,y)\in [3]\times [4,6]\right\}\,\ne \,\varnothing\).
Lemma 2.43
Let U be a word over \({\mathcal{S}}\cup {\mathcal{C}}\). Then \(U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,3}\circ {{\mathfrak{S}}}_{4,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\setminus {\mathcal{L}}({{\mathfrak{S}}}_{1,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\) if and only if \(U\in {\mathcal{N}}\) and U has a 2 × 4 pattern with \({\mathfrak{p}}(U)\cap \left\{\left\{x,y\right\}\,;\,(x,y)\in ([3],[4,6])\right\}=\varnothing\).
Theorem 2.44
Let U be a word over \({\mathcal{S}}\cup {\mathcal{C}}\). Then \(U\in {\mathcal{L}}({{\mathfrak{S}}}_{1,3}\circ {{\mathfrak{S}}}_{4,9}\circ {{\mathfrak{S}}}_{10,15}\circ {\mathfrak{C}})\) if and only if \(U\in {\mathcal{N}}\).
Proof
If ∣U∣ = 1 then the result follows from Lemma 2.40. If ∣U∣ > 1, then U has a 2 × 2 × 2 or a 2 × 4 pattern and the result follows from Proposition 2.39 and Lemmas 2.41, 2.42 and 2.43.□
Lower bounds
Recall that the distance between operators U and V is defined as \(\parallel U-V\parallel =\sup \left\{\parallel Uv-Vv\parallel \,;\,\parallel v\parallel =1\right\}\). Because \({\mathcal{G}}\) is universal, for every ϵ > 0 and every element U ∊ SU(4), there exists \(V\in {\mathcal{G}}\) such that ∥U − V∥ ≤ ϵ. In such a case we say that V is an ϵ-approximation of U. We now take advantage of Theorem 2.44 to count Clifford+CS operators and use these results to derive a worst-case lower bound on the CS-count of approximations.
Lemma 2.45
Let n ≥ 1. There are 86400(3 ⋅ 8n − 2 ⋅ 4n) Clifford+CS operators of CS-count exactly n.
Proof
Each Clifford+CS operator is represented by a unique normal form and this representation is CS-optimal. Hence, to count the number of Clifford+CS operators of CS-count n, it suffices to count the normal forms of CS-count n. By Theorem 2.44, and since Clifford operators have CS-count 0, a normal form of CS-count n is a word
such that \({w}_{1}\in {\mathcal{L}}({{\mathfrak{S}}}_{1,3})\), \({w}_{2}\in {\mathcal{L}}({{\mathfrak{S}}}_{4,9})\), \({w}_{3}\in {\mathcal{L}}({{\mathfrak{S}}}_{10,15})\), \({w}_{4}\in {\mathcal{L}}({\mathfrak{C}})\) and the CS-counts of w1, w2, and w3 sum to n. There are
words of the form of Eq. (19) such that exactly one of w1, w2, or w3 is not ε. Similarly, there are
words of the form of Eq. (19) such that exactly two of w1, w2, or w3 are not ε. Finally, the number of words of the form of Eq. (19) such that w1, w2, and w3 are not ε is
Summing Eqs. (20), (21) and (22) and applying the geometric series formula then yields the desired result. □
Corollary 2.46
For \(n\in {\mathbb{N}}\), there are \(\frac{46080}{7}(45\cdot {8}^{n}-35\cdot {4}^{n}+4)\) distinct Clifford+CS operators of CS-count at most n.
Proof
Recall that the Clifford+CS operators of CS-count 0 are exactly the Clifford operators and that \(| {\mathcal{C}}| =92160\). The result then follows from Lemma 2.45 and the geometric series formula.
Proposition 2.47
For every \(\epsilon \in {{\mathbb{R}}}^{ \,{>}\,0}\), there exists U ∊ SU(4) such that any Clifford+CSϵ-approximation of U has CS-count at least \(5{{\rm{log}}}_{2}(1/\epsilon )-0.67\).
Proof
By a volume counting argument. Each operator must occupy an ϵ-ball worth of volume in 15-dimensional SU(4) space, and the sum of all these volumes must add to the total volume of SU(4) which is \((\sqrt{2}{\pi }^{9})/3\). The number of circuits up to CS-count n is taken from Corollary 2.46 (we must divide the result by two to account for the absence of overall phase ω in the special unitary group) and a 15-dimensional ϵ-ball has a volume of
Let U be an element of \({\mathcal{G}}\) of determinant 1. By Eq. (1) of Section “Generators”, U can be written as
where \(k\in {\mathbb{N}}\) and the entries of M belong to \({\mathbb{Z}}\left[i\right]\). We can therefore talk about the least denominator exponent of the SU(4) representation of U. We finish this section by relating the least denominator exponent of the SU(4) representation of U and the CS-count of the normal form of U.
Proposition 2.48
Let U be an element of \({\mathcal{G}}\) of determinant 1, let k be the least denominator exponent of the SU(4) representation of U, and let \(k^{\prime}\) be the CS-count of the normal form of U. Then
Proof
The CS-count of the normal form of U is equal to the least denominator exponent of the SO(6) representation of U. Eq. (11) then implies the upper bound for \(k^{\prime}\). Likewise, examination of Theorem 2.44 reveals that the CS operators in the circuit for U must be separated from one another by a Clifford with a least denominator exponent of at most 2 in its unitary representation. Combining this with the fact that the largest least denominator exponent of an operator in \({\mathcal{C}}\) is 3, we arrive at the lower bound for \(k^{\prime}\). □
Remark 2.49
It was established in ref. 8 that, for single-qubit Clifford+T operators of determinant 1, there is a simple relation between the least denominator exponent of an operator and its T-count: if the least denominator exponent of the operator is k, then its T-count is 2k − 2 or 2k. Interestingly, this is not the case for Clifford+CS operators in SU(4), as suggested by Proposition 2.48. Clearly, the CS-count of an operator always scales linearly with the least denominator exponent of its unitary representation. For large k, computational experiments with our code38 suggest that most operators are such that \(k^{\prime} \approx k\), though there are examples of operators with \(k^{\prime} \approx 2k\). One example of such an operator is \({\left[R(X\otimes I,I\otimes Z)R(X\otimes I,I\otimes X)R(Z\otimes I,I\otimes X)R(Z\otimes I,I\otimes Z)\right]}^{m}\) for \(m\in {\mathbb{N}}\).
Discussion
We described an exact synthesis algorithm for a fault-tolerant multi-qubit gate set which is simultaneously optimal, practically efficient, and explicitly characterizes all possible outputs. The algorithm establishes the existence of a unique normal form for two-qubit Clifford+CS circuits. We showed that the normal form for an operator can be computed with a number of arithmetic operations linear in the gate-count of the output circuit. Finally, we used a volume counting argument to show that, in the typical case, ϵ-approximations of two-qubit unitaries will require a CS-count of at least \(5{{\rm{log}}}_{2}(1/\epsilon )\).
We hope that the techniques developed in the present work can be used to obtain optimal multi-qubit normal forms for other two-qubit gate sets, such as the two-qubit Clifford+T-gate set. Indeed, it can be shown that the SO(6) representation of Clifford+T operators are exactly the set of SO(6) matrices with entries in the ring \({\mathbb{Z}}[1/\sqrt{2}]\). Further afield, the exceptional isomorphism for SU(8) could potentially be leveraged to design good synthesis algorithms for three-qubit operators. Such algorithms would provide a powerful basis for more general quantum compilers.
An interesting avenue for future research is to investigate whether the techniques and results presented in this paper can be used in the context of synthillation. Quantum circuit synthesis and magic state distillation are often kept separate. But it was shown in ref. 41 that performing synthesis and distillation simultaneously (synthillation) can lead to overall savings. The analysis presented in ref. 41 uses T gates and T states. Leveraging higher-dimensional synthesis methods such as the ones presented here, along with distillation of CS states, could yield further savings.
Methods
All results were produced theoretically or computationally, with the requisite methods described at length in each section.
Code availability
The Mathematica package referenced throughout the paper and its documentation are publically available from the repository at ref. 38.
References
Reichardt, B. W. Quantum universality from magic states distillation applied to CSS codes. Quantum Inf. Process. 4, 251–264 (2005).
Blass, A., Bocharov, A. & Gurevich, Y. Optimal ancilla-free Pauli+V circuits for axial rotations. J. Math. Phys. 56, 122201 (2014).
Bocharov, A., Gurevich, Y. & Svore, K. M. Efficient decomposition of single-qubit gates into V basis circuits. Phys. Rev. A 88, 012313 (2013).
Forest, S., Gosset, D., Kliuchnikov, V. & McKinnon, D. Exact synthesis of single-qubit unitaries over Clifford-cyclotomic gate sets. J. Math. Phys. 56, 082201 (2015).
Kliuchnikov, V., Maslov, D. & Mosca, M. Fast and efficient exact synthesis of single-qubit unitaries generated by Clifford and T gates. Quantum Inf. Comput. 13, 607–630 (2013).
Kliuchnikov, V. & Yard, J. A framework for exact synthesis (2015). Preprint.
Ross, N. J. Optimal ancilla-free Clifford+V approximation of z-rotations. Quantum Inf. Comput. 15, 932–950 (2015).
Ross, N. J. & Selinger, P. Optimal ancilla-free Clifford+T approximation of z-rotations. Quantum Inf. Comp. 16, 901–953 (2016).
Bocharov, A., Cui, X., Kliuchnikov, V. & Wang, Z. Efficient topological compilation for a weakly integral anyonic model. Phys. Rev. A 93, 012313 (2016).
Glaudell, A. N., Ross, N. J. & Taylor, J. M. Canonical forms for single-qutrit Clifford+T operators. Ann. Phys. 406, 54–70 (2019).
Kliuchnikov, V., Bocharov, A. & Svore, K. M. Asymptotically optimal topological quantum compiling. Phys. Rev. Lett. 112, 140504 (2014).
Prakash, S., Jain, A., Kapur, B. & Seth, S. Normal form for single-qutrit Clifford+T operators and synthesis of single-qutrit gates. Phys. Rev. A 98, 032304 (2018).
Kliuchnikov, V., Bocharov, A., Roetteler, M. & Yard, J. A framework for approximating qubit unitaries (2015). Preprint.
Kliuchnikov, V., Maslov, D. & Mosca, M. Practical approximation of single-qubit unitaries by single-qubit quantum Clifford and T circuits. IEEE T. Comput. 65, 161–172 (2016).
Shende, V. V., Markov, I. L. & Bullock, S. S. Minimal universal two-qubit controlled-NOT-based circuits. Phys. Rev. A 69, 062321 (2004).
Zhang, J., Vala, J., Sastry, S. & Whaley, K. B. Geometric theory of nonlocal two-qubit operations. Phys. Rev. A 67, 042313 (2003).
Amy, M., Glaudell, A. N. & Ross, N. J. Number-theoretic characterizations of some restricted Clifford+T circuits. Quantum 4, 252 (2020).
Amy, M., Maslov, D. & Mosca, M. Polynomial-time T-depth optimization of Clifford+T circuits via matroid partitioning. IEEE T. Comput. Aid. D. 33, 1476–1489 (2014).
Amy, M., Maslov, D., Mosca, M. & Roetteler, M. A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE T. Comput. Aid. D. 32, 818–830 (2013).
Giles, B. & Selinger, P. Exact synthesis of multiqubit Clifford+T circuits. Phys. Rev. A 87, 032332 (2013).
Gosset, D., Kliuchnikov, V., Mosca, M. & Russo, V. An algorithm for the T-count. Quantum Inf. Comput. 14, 1261–1276 (2014).
Heyfron, L. E. & Campbell, E. T. An efficient quantum compiler that reduces T-count. Quantum Sci. Technol. 4, 015004 (2018).
Kissinger, A. & van de Wetering, J. Reducing the number of non-Clifford gates in quantum circuits. Phys. Rev. A 102, 022406 (2020).
Matteo, O. D. & Mosca, M. Parallelizing quantum circuit synthesis. Quantum Sci. Technol. 1, 015003 (2016).
Meuli, G., Soeken, M. & Micheli, G. D. SAT-based {CNOT, T} quantum circuit synthesis. In Lecture Notes in Computer Science, RC ’17, 175–188 (Springer International Publishing, 2018).
Mosca, M. & Mukhopadhyay, P. A polynomial time and space heuristic algorithm for T-count (2020). Preprint.
Zhang, F. & Chen, J. Optimizing T gates in Clifford+T circuit as π/4 rotations around Paulis (2019). Preprint.
Giles, B. & Selinger, P. Remarks on Matsumoto and Amano’s normal form for single-qubit Clifford+T operators (2013). Preprint.
Selinger, P. Efficient clifford+T approximation of single-qubit operators. Quantum Inf. Comput. 15, 159–180 (2015).
Beverland, M., Campbell, E., Howard, M. & Kliuchnikov, V. Lower bounds on the non-Clifford resources for quantum computations. Quantum Sci. Technol. 5, 035009 (2020).
Haah, J. & Hastings, M. B. Codes and protocols for distilling T, controlled-S, and Toffoli gates. Quantum 2, 71 (2018).
Cross, A. W. et al. Scalable randomised benchmarking of non-Clifford gates. npj Quantum Inf. 2, 1–5 (2016).
Garion, S. & Cross, A. W. Synthesis of CNOT-dihedral circuits with optimal number of two qubit gates. Quantum 4, 369 (2020).
Garion, S. et al. Experimental implementation of non-Clifford interleaved randomized benchmarking with a controlled-\({\mathcal{S}}\) gate. Phys. Rev. Res. 3, 013204 (2021).
Sheldon, S., Magesan, E., Chow, J. M. & Gambetta, J. M. Procedure for systematically tuning up cross-talk in the cross-resonance gate. Phys. Rev. A 93, 060302 (2016).
Foxen, B. et al. Demonstrating a continuous set of two-qubit gates for near-term quantum algorithms. Phys. Rev. Lett. 125, 120504 (2020).
Xu, Y. et al. High-fidelity, high-scalability two-qubit gate scheme for superconducting qubits. Phys. Rev. Lett. 125, 240503 (2020).
Glaudell, A. N., Ross, N. J. & Taylor, J. M. GaussSynth. https://doi.org/10.5281/zenodo.4549819. (2020).
Tilma, T. & Sudarshan, E. Generalized Euler angle parametrization for SU(N). J. Phys. A Math. Gen. 35, 10467 (2002).
Sipser, M. Introduction to the Theory of Computation, 1st edn (International Thomson Publishing, 1996).
Campbell, E. T. & Howard, M. Unified framework for magic state distillation and multiqubit gate synthesis with reduced resource cost. Phys. Rev. A 95, 022316 (2017).
Acknowledgements
A.N.G. was partially supported by the Princeton Center for Complex Materials, a MRSEC supported by NSF grant DMR 1420541. N.J.R. was partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC), funding reference number RGPIN-2018-04064. We would like to thank Matthew Amy, Xiaoning Bian, and Peter Selinger for helpful discussions. In addition, we would like to thank the anonymous reviewers whose comments greatly improved the paper.
Author information
Authors and Affiliations
Contributions
All authors researched, collated, and wrote this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Glaudell, A.N., Ross, N.J. & Taylor, J.M. Optimal two-qubit circuits for universal fault-tolerant quantum computation. npj Quantum Inf 7, 103 (2021). https://doi.org/10.1038/s41534-021-00424-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00424-z
This article is cited by
-
T-count and T-depth of any multi-qubit unitary
npj Quantum Information (2022)