Intensity modulator for secure, stable, and high-performance decoy-state quantum key distribution

Abstract

The decoy-state method substantially improves the performance of quantum key distribution (QKD) and perfectly solves crucial issues caused by multiphoton pulses. In recent years, the decoy-state method has occupied a key position in practicality, and almost all the QKD systems have employed the decoy-state method. However, the imperfections of traditional intensity modulators limit the performance of the decoy-state method and bring side channels. In this work, a special intensity modulator and its accompanying modulation method are designed and experimentally verified for the secure, stable, and high-performance decoy-state QKDs. The experimental result indicates that its stable and adjustable intensities, convenient two-level modulation, inherently high speed, and compact structure is extremely fit for future trends and will help the decoy-state method to be perfectly applied to QKD systems.

Introduction

Quantum key distribution (QKD)¹ provides a way for two legitimate remote users, namely, Alice and Bob, to share secret keys with information-theoretic security^2,3,4,5,6. However, this security relies on the single-photon state while the ideal single-photon sources are not yet practically useful. As an alternative, a revolutionary method named the decoy-state method^7,8,9 is employed in almost all practical QKD systems. This method allows a practical system based on weak coherent pulse sources to achieve the security performance of a single-photon QKD, which is a perfect combination of theory and practice.

The decoy-state method significantly improves the secret key rate and achievable distance of practical systems, but the legitimate users have to modulate several different intensities^{10,11,12,13,14,15,16,17,18,19,20,21,22,23,24} precisely and independently. Usually, a decoy-state QKD requires weak coherent pulses with three or more different intensities. Some systems also require a special decoy state named vacuum state. Compared with classic optical communications, the intensity modulation in QKD systems is more difficult since the conflict between completely random modulation and finite modulation bandwidth.

A good intensity modulation for decoy-state QKD should be secure, stable, and flexible. The ‘secure’ is a basic requirement that the modulation should not violate the security assumptions of the QKD. The ‘stable’ means the output intensities should be insensitive to disturbances in an electric signal. The ‘flexible’ is that the manipulation should be as simple as possible. Meanwhile, it is important for a good intensity modulation that it should not be a short slab of the system performance. However, existing modulators cannot meet all the above requirements at the same time. The most widely used commercial LiNbO₃-based Mach–Zehnder interferometer (MZI) is extremely sensitive to the electric signal disturbance, which violates the condition of ‘stable’, brings intensity fluctuation, and reduces the secret key rate^{22,25,26,27,28}. To make the matter worse, a special intensity fluctuation named patterning effect²⁹ introduces correlation of adjacent signals, which provides additional information and allows Eve to perform sophisticated attacks since current security analysis usually assumes independent and identically distributed (i. i. d) pulses. The imperfection of the MZI modulator has shaken the basis of the QKD.

To fill the loophole in the intensity modulation, two countermeasures are proposed. The first one is a post-processing method²⁹. It works by discarding some pulses depending on the state of predecessor and successor. Another countermeasure is an intensity modulator based on Sagnac interferometer³⁰. It is used as a secure two-level intensity modulator for QKD, not only can mitigate the patterning effect but also is immune to the DC drift. The two countermeasures are secure and convenient but not so friendly to high-performance QKDs. The post-processing method ineluctably reduces the secret key rate since it discards too many key bits while the higher key rate is what people pursue in the QKD field. The Sagnac modulator is also not so suitable for the decoy-state method since its two-level intensity modulation and fixed stable intensities cannot meet the requirement of more than two adjustable intensities. Besides, the worst of it is that its common-path mechanism brings an inherent speed limit. Considering that the high-speed system is a trend of the QKD field, the Sagnac modulator may become a short slab in QKD systems in the future.

An interesting question is whether we can design an intensity modulator that can generate three, four, or even more stable intensities, and these stable intensities should be tunable to optimize intensities for improving the secret key rate^21,31,32,33. Beyond that, it is lacing on the cake if its driving-voltages only switch between two different voltages, which would significantly reduce the modulation difficulty. Fortunately, the answer is yes. In this work, an intensity modulator named multipath Mach-Zehnder interferometer (MMZI) and its accompanying modulation method that meets all the above requirements are proposed. By working only at the ‘half-wave points’, the MMZI can generate a variety of different stable intensities to mitigate the intensity fluctuation and the patterning effect for secure and robust QKD systems. The MMZI is also inherently high-speed and facility for integration due to the traveling-wave modulation and its compact structure.

Results

Most QKD systems generate the decoy states by commercial LiNbO₃-based MZIs, in which an input pulse is first split into two parts by a 1 × 2 splitter and then recombined by a 2 × 1 coupler. The splitting ratios of the splitter and the coupler of commercial MZIs are both $\frac{1}{2}$. Thus, the output intensity I(α) is

$$I(\alpha )=\frac{{\mu }_{\rm{in}}}{2}\left(1+\cos \alpha \right),$$

(1)

where the α is the phase difference of the two paths and the μ_in is the input intensity. In many decoy-state QKD systems, commercial MZIs are applied to produce a signal state μ_s, a decoy state μ_d and a vacuum state μ_v = 0^20,23,34. As illustrated in Fig. 1, the signal state corresponds to the flat peak point S and the decoy state corresponds to the slope point D. We define the points with 0 derivative as stable points. Here the point S is a stable point. It is obvious that comparing with the stable points, the slope points are more sensitive to disturbances such as timing jitter and electric waveform distortion, which would cause unforeseeable fluctuation on μ_d. Especially, in high-speed systems^35,36,37, a finite modulation bandwidth leads to a correlation between adjacent signals, namely, the intensity of a pulse would be correlated with its previous one, which violates the important i.i.d. assumption.

Fig. 1: The voltage response curve of a commercial LiNbO₃-based MZI with 50:50 splitting ratio.

With the same voltage disturbance ΔV, the intensity difference ΔI on the slope point D is significantly larger than it on the stable point S. The V_π denotes the half-wave voltage.

To make QKD systems more secure and robust, we present a MMZI and an accompanying modulation method, which can be perfectly applied to decoy-state QKD systems. By working at the half-wave voltage, the interferometer can generate several stable intensities to mitigate the intensity fluctuation and the patterning effect for the security. As illustrated in Fig. 2, the interferometer consists of an 1 × N splitter, a N × 1 coupler and N parallel paths. One of the path (path-0) includes a variable optical attenuator (VOA) to tune its attenuation ratio η and others paths (path-1 to N − 1) each has a built-in phase modulator to shift the relative phases α_k for k ∈ {1, 2....N − 1}. An input coherent pulse with intensity μ_in is first split by the 1 × N splitter whose splitting ratio to the path-k is denoted by ${t}_{k}^{\prime}$ and then modulated in each path. After that, the pulses in each path couple and interfere in the N × 1 coupler whose splitting ratio to the path-k is denoted by ${t}_{k}^{^{\prime\prime} }$. To make the following formulas clearer, we define ${t}_{k}=\sqrt{{t}_{k}^{\prime}{t}_{k}^{^{\prime\prime} }}$.

Fig. 2: The structure of our multipath Mach-Zehnder interferometer.

In this modulator, input pulses are split by an 1 × N splitter and enter into N different paths. The path-0 has a VOA to attenuate the pulse and the path-1 to N − 1 each has a phase modulator to modulate the relative phases. Finally, the split pulses interfere in a N × 1 coupler. P path; BS beam splitter; PM phase modulator; VOA variable optical attenuator.

Note that since QKD systems have an attenuator to attenuate the intensity to single-photon level^{34,35,36,38,39,40,41,42,43,44,45,46,47}, we ignore the insertion loss in the follows. The output pulse of the path-0 and path-k for k ∈ {1, 2, ...., N − 1} are, respectively, $\left|\sqrt{\eta }{t}_{0}\sqrt{{\mu }_{\rm{in}}}\right\rangle$ and $\left|{t}_{k}{e}^{i{\alpha }_{k}}\sqrt{{\mu }_{\rm{in}}}\right\rangle$. After the interference, the MMZI outputs:

$$\left|\sqrt{{\mu }_{\rm{out}}}\right\rangle =\left|\,\left(\sqrt{\eta }{t}_{0}+\mathop{\sum }\limits_{k=1}^{N-1}{t}_{k}{e}^{i{\alpha }_{k}}\right)\sqrt{{\mu }_{\rm{in}}}\right\rangle .$$

(2)

The output intensity can be regarded as a function of relative phases:

$$\begin{array}{l}\,I({\alpha }_{1},{\alpha }_{2},....,{\alpha }_{N-1})=\langle \sqrt{{\mu }_{\rm{out}}}| \sqrt{{\mu }_{\rm{out}}}\rangle \\ \,\qquad\qquad\qquad\qquad\quad={\mu }_{\rm{in}}\left[\eta {{t}_{0}}^{2}+2\sqrt{\eta }{t}_{0}\mathop{\sum }\limits_{k=1}^{N-1}{t}_{k}\cos {\alpha }_{k}\right.\\ \,\qquad\qquad\qquad\qquad\qquad\left.+\mathop{\sum }\limits_{k=1}^{N-1}{{t}_{k}}^{2}+\mathop{\sum }\limits_{k=1}^{N-1}\mathop{\sum }\limits_{l=k+1}^{N-1}2{t}_{k}{t}_{l}\cos ({\alpha }_{k}-{\alpha }_{l})\right].\end{array}$$

(3)

Since the condition of a stationary point is that all its partial derivatives should be 0, namely, the

$$\begin{array}{l}\,\frac{\partial I({\alpha }_{1},{\alpha }_{2},....,{\alpha }_{N-1})}{\partial {\alpha }_{k}} \,=-\left[2\sqrt{\eta }{t}_{0}{t}_{k}\sin {\alpha }_{k}+\mathop{\sum }\limits_{l}^{l\ne k}2{t}_{k}{t}_{l}\sin ({\alpha }_{k}-{\alpha }_{l})\right]\\ \qquad\qquad\quad\quad\,\,\,\,=0,\,{\rm{for}}\ k\in \{1,2,....,N-1\},\end{array}$$

(4)

the ∀α_k ∈ {0, π} are general solutions of Eq. (4). For simplicity, we define these general solutions as the ‘half-wave points’ in the follows. In another word, when the voltages on each path is V₀ or V_π, the output intensity would be stable. Since each α_k can be tuned to be 0 or π, there are 2^N−1 stable intensities, which can be denoted by ${I}_{1},{I}_{2},....,{I}_{{2}^{N-1}}$.

For a specific decoy-state QKD system that requires optimized intensities μ₁, μ₂, ...., μ_n, without loss of generality, we assume that the {I₁, I₂, ...., I_n} and {μ₁, μ₂, ...., μ_n} are sorted in descending order. A user should firstly find a set of t_k and a η according to Eqs. (2) and (3) to make

$$\frac{{I}_{i}}{{I}_{1}}=\frac{{\mu }_{i}}{{\mu }_{1}},{\rm{for}}\ i\in \{2....n\}.$$

(5)

After that, the user adjusts the attenuator in the QKD system to make the maximum intensity I₁, which always corresponds to the point ∀α_k = 0, equals to the μ₁. Naturally the other stable intensities equal to the other optimized decoy states. We take the optimized intensity sets [${\mu }_{s}=0.015,\,{\mu }_{{d}_{1}}=0.006,\,{\mu }_{{d}_{2}}=0.002,\,{\mu }_{v}=0$] and [${\mu }_{s}=0.43,\,{\mu }_{{d}_{1}}=0.19,\,{\mu }_{{d}_{2}}=0.05,\,{\mu }_{v}=0$] in the recent twin-field QKD experiments^45,46 as examples. We employ a three-path MMZI and denote its four stable intensities as I(0, 0), I(0, π), I(π, 0) and I(π, π), respectively. To generate the first optimized intensity set, an user should firstly set the splitting ratios and fine-tune the VOA to [$\sqrt{\eta }{t}_{0}=0.5$, t₁ = 0.3170, t₂ = 0.1830] to make the I(0, π)/I(0, 0) = 0.4019, I(π, 0)/I(0, 0) = 0.1122 and I(π, π) = 0. After that, he (she) adjust the attenuator in the QKD system to make I(0, 0) = μ_s = 0.015, then naturally, the $I(0,\pi )={\mu }_{{d}_{1}}=0.006$, $I(\pi ,0)={\mu }_{{d}_{2}}=0.002$, and I(π, π) = μ_v = 0. Similarly, to generate the second optimized intensity set, an user can set the t_k and η to [$\sqrt{\eta }{t}_{0}=0.5$, t₁ = 0.3305, t₂ = 0.1695] and adjust the attenuator in the QKD system to make $I(0,\pi )={\mu }_{{d}_{1}}=0.43$. Then the $I(0,\pi )={\mu }_{{d}_{1}}=0.19$, $I(\pi ,0)={\mu }_{{d}_{2}}=0.05$and I(π, π) = μ_v = 0.

It is worth noting that, the stable intensities are adjusted by setting the splitting ratios and tuning the VOA. The MMZI would only has a limited tuning range when the splitting ratios are fixed. A more flexible structure with a larger tuning range can be achieved by adding VOA in each path. The details are introduced in the Discussion.

Discussion

The stable intensities of the MMZI can be fine-tuned by the built-in VOA so that users can optimize the secret key rate. However, the tuning range is limited. In this section, another structure for improving the tuning range is proposed., As illustrated in Fig. 3, each path owns a VOA. The attenuation ratio of the path-k is denoted by η_k for k ∈ {0, 1, 2, ...., N − 1}. By adjusting these η_k, the ratio of the stable intensities can be modified flexibly to meet the need for intensity optimization.

Fig. 3: A MMZI structure for improving the tuning range.

In this scheme, each path owns a VOA. Adjusting attenuation ratios of these VOAs is equivalent to adjusting splitting ratios of the splitter and the coupler.

In order to simplify the problem, we assume that the splitter has a balanced splitting ratio, namely, t_k = 1/N for k ∈ {0, 1, 2, ...., N − 1}. The output state of the path-0 and the path-k (k ∈ {1, 2, ...., N − 1}) are denoted by $\left|\frac{1}{N}\sqrt{{\eta }_{0}{\mu }_{\rm{in}}}\right\rangle$ and $|\frac{{e}^{i{\alpha }_{k}}}{N}\sqrt{{\eta }_{k}{\mu }_{\rm{in}}}\rangle$ respectively. the output state of the interferometer is:

$$\left|\sqrt{{\mu }_{\rm{out}}}\right\rangle =\left|\,\frac{1}{N}\left(\sqrt{{\eta }_{0}}+\mathop{\sum }\limits_{k=1}^{N-1}{\eta }_{k}{e}^{i{\alpha }_{k}}\right)\sqrt{{\mu }_{\rm{in}}}\right\rangle .$$

(6)

The output intensity is:

$$\begin{array}{l}\,I({\alpha }_{1},{\alpha }_{2},....,{\alpha }_{N-1})=\langle \sqrt{{\mu }_{\rm{out}}}| \sqrt{{\mu }_{\rm{out}}}\rangle \\ \qquad\qquad\qquad\qquad\quad\,=\frac{{\mu }_{\rm{in}}}{{N}^{2}}\left({\eta }_{0}+2\sqrt{{\eta }_{0}}\mathop{\sum }\limits_{k=1}^{N-1}\sqrt{{\eta }_{k}}\cos {\alpha }_{k}\right.\\ \,\left.\qquad\qquad\qquad\qquad\qquad\,+\mathop{\sum }\limits_{k=1}^{N-1}{\eta }_{k}+\mathop{\sum }\limits_{k=1}^{N-1}\mathop{\sum }\limits_{l=k+1}^{N-1}2\sqrt{{\eta }_{k}{\eta }_{l}}\cos ({\alpha }_{k}-{\alpha }_{l})\right).\end{array}$$

(7)

The outputs of the stable points mainly depend on η_k for k ∈ {0, 1, 2, ...., N − 1}, namely, they can be modified flexibly by adjusting the built-in VOAs.

The partial derivative equations of Eq. (7) is expressed as:

$$\begin{array}{l}\frac{\partial I({\alpha }_{1},{\alpha }_{2},....,{\alpha }_{N-1})}{\partial {\alpha }_{k}}= -\frac{{\mu }_{\rm{in}}}{{N}^{2}}\left[2\sqrt{{\eta }_{0}{\eta }_{k}}\sin {\alpha }_{k}+\mathop{\sum }\limits_{l}^{l\ne k}2\sqrt{{\eta }_{k}{\eta }_{l}}\sin ({\alpha }_{k}-{\alpha }_{l})\right]\\ \,\,\,\quad\quad\qquad\qquad=0;{\rm{for}}\ k\in \{1,2,....,N-1\}.\end{array}$$

(8)

Significantly, the general solution is also ∀α_k ∈ {0, π} for k ∈ {1, 2, ...., N − 1}.

With the development of high-speed QKD systems, the widely used commercial LiNbO₃ MZIs are increasingly difficult to meet the need for security, robustness, and flexibility. To improve the performance of the decoy-state QKD and make it more practical, a MMZI and its accompanying modulation method are proposed in this work. Our method can generate 2^N−1 different stable intensities to mitigate the intensity fluctuation and the patterning effect from imperfect modulation signals. The flexibility of its ‘half-wave modulation’ and tunable outputs makes it suitable for different protocols and systems. Its compact structure makes it easy to integrate. Besides, it is inherently high-speed due to the traveling-wave modulation. A user may generate stable decoy states by cascading several MZIs. However, in this scheme, the splitting ratio of each MZI must be specially designed. Considering that almost all commercial MZIs have a symmetric splitting ratio, each MZI in the series must be customized, which would increase difficulty and cost. Even if the customized MZIs are employed, the stable intensities of the cascade MZI design are fixed when connecting N MZIs in series, the user can generate at most 2^N stable intensities. By contrast, the user can build 2N-path MMZI by connecting N MZIs in parallel, in another word, he (she) can generate at most 2^2N−1 stable intensities, which is much more than connecting in series. Compared with cascading several customized MZIs, a 3-path MMZI (DPMZI or connecting two commercial MZI in parallel) can generate 4 stable intensities and the intensities are tunable, which is much more flexible and convenient in practical applications.

We have also experimentally demonstrated the modulation method by an commercial dual-parallel MZI (DPMZI) which could be regarded as a special case of the MMZI. We measured a random sequence consisting of signal, decoy, and vacuum state. The result suggests that our method can effectively mitigate the influence of the patterning effect. We have also demonstrated adjusting the ratio ${\mathcal{R}}$ to verify its convenience for intensity optimization. The details could be found in METHODS. The result indicates that our interferometer and modulation method are feasible in practice and will be secure, robust, and flexible for decoy-state QKD systems. Since its compact structure is easy to integrate, we believe that an integrated MMZI can be perfectly applied in high-speed decoy-state QKD systems and help the practical QKDs to achieve the optimized performance.

Methods

Experimental demonstration

In this section, we demonstrate the MMZI and its accompanying modulation method by a commonly used three-intensity decoy-state method^17,22,48,49 which consists of a signal state, a decoy state, and a vacuum state. An integrated commercial modulator named DPMZI^50,51,52, which can be regarded as a special case of our MMZI is employed in the demonstration. As illustrated in Fig. 4, a DPMZI consists of two parallel sub-MZIs, one of which can be regarded as a VOA and the other one can be regarded as two independent paths. For simplicity, we use VOA to refer to the first sub-MZI. In other words, the DPMZI can be regarded as an equivalent of our modulator with three paths. Since all beam splitters in DPMZI have a 50:50 ratio, the splitting ratio t₀, t₁, and t₂ are fixed to, respectively, 0.5, 0.25 and 0.25. The output of DPMZI is written as:

$$\left|\sqrt{{\mu }_{\rm{out}}}\right\rangle =\left|\left(\frac{1}{2}\sqrt{\eta }+\frac{1}{4}{e}^{i{\alpha }_{1}}+\frac{1}{4}{e}^{i{\alpha }_{2}}\right)\sqrt{{\mu }_{\rm{in}}}\right\rangle .$$

(9)

The output intensity is a function of α₁ and α₂, which is written as:

$$\begin{array}{l}I({\alpha }_{1},{\alpha }_{2})=\frac{{\mu }_{\rm{in}}}{4}\left[\eta +\sqrt{\eta }(\cos {\alpha }_{1}+\cos {\alpha }_{2})\right.\\ \,\qquad\qquad\quad\left.+\frac{1}{2}+\frac{1}{2}\cos ({\alpha }_{1}-{\alpha }_{2})\right].\end{array}$$

(10)

As discussed above, the half-wave points are stable. The I(0, 0) is the maximum intensity, which is regarded as the signal state μ_s. The other half-wave points can be employed as decoy states, here we select the I(0, π) as the decoy state μ_d. Since the splitting ratios of the integrated commercial DPMZI have been fixed (namely, we cannot adjust splitting ratios to make the vacuum state on a half-wave point), we employ a particular solution, which is the solution of the equation set

$$\begin{array}{ll}&\frac{\partial I({\alpha }_{1},{\alpha }_{2})}{\partial {\alpha }_{1}}=-\frac{1}{4}\left[\sqrt{\eta }\sin {\alpha }_{1}+\frac{1}{2}\sin ({\alpha }_{1}-{\alpha }_{2})\right]=0;\\ &\frac{\partial I({\alpha }_{1},{\alpha }_{2})}{\partial {\alpha }_{2}}=-\frac{1}{4}\left[\sqrt{\eta }\sin {\alpha }_{2}+\frac{1}{2}\sin ({\alpha }_{2}-{\alpha }_{1})\right]=0;\\ &I({\alpha }_{1},{\alpha }_{2})=\frac{{\mu }_{\rm{in}}}{4}\left[\eta +\sqrt{\eta }(\cos {\alpha }_{1}+\cos {\alpha }_{2})+\right.\\ &\left.\frac{1}{2}+\frac{1}{2}\cos ({\alpha }_{1}-{\alpha }_{2})\right]=0,\end{array}$$

as the vacuum state. Experimentally, we can obtain the vacuum point by scanning the driving-voltage of path-1 and 2 alternately and taking the voltage which minimizes the output intensity in each turn.

As illustrated in Fig. 5. The point S (α₁ = 0, α₂ = 0) is a peak point which corresponds to the signal state μ_s; The point D (α₁ = 0, α₂ = π) is a saddle point that is selected to generate the decoy state μ_d. The point V is a trough point which corresponds to the vacuum state. Now that the t_k are fixed, the stable intensities are $I(0,0)=\frac{{\mu }_{\rm{in}}}{4}{(1+\sqrt{\eta })}^{2}$ and $I(0,\pi )=\frac{{\mu }_{\rm{in}}}{4}\eta$, which are functions of the η. Defining that ${\mathcal{R}}={\mu }_{d}/{\mu }_{s}$, the user can adjust the VOA to $\eta ={(\frac{\sqrt{{\mathcal{R}}}}{1-\sqrt{{\mathcal{R}}}})}^{2}$ to make $I(0,\pi )/I(0,0)={\mathcal{R}}$.

Fig. 4: The figure depicts the structure of the DPMZI, which contains two parallel sub-MZI.

In our modulation method, one of the MZIs is regarded as a VOA.

In our experimental demonstration, a series of 50 ps light pulses generated from a 1 GHz high-speed picosecond laser were fed to a DPMZI (produced by FUJITSU OPTICAL COMPONENTS LIMITED and the model is FTM7960EX). A 5 GS/s-sampling-rate arbitrary waveform generator with two RF-amplifiers was applied to drive the interferometer. A pseudo-random number sequence was employed to the arbitrary waveform generator to generate random encoding signals. Complementary encoding signals similar to ref. ²⁹ were employed to meet the need of the RF-amplifiers. On the detection side, the modulated pulses were detected by a 20-GHz-bandwidth high-speed photodiode and recorded by a 12.5-GHz-bandwidth oscilloscope. Since it is assumed that the average intensity reflects the mean photon number in the quantum pulses through heavy attenuation linearly²⁹, we measured the intensities before they are attenuated to single-photon magnitude and calculated the intensity by the area of the pulse traced by the oscilloscope.

To demonstrate the ability to mitigate the patterning effect, a random sequence consisting of signal, decoy, and vacuum state was measured and 20,000 pulses were collected for statistical analysis. A short subset of the tracing result was shown in Fig. 6. To show the flexibility of tuning the ratio of signal and decoy state, we measured the average intensities of different patterns with different η. We adjusted the η to make the ${\mathcal{R}}={\mu }_{d}/{\mu }_{s}=0.24$, 0.21, 0.18, and 0.12 as the interval of 0.1–0.25 is widely used in decoy-state QKDs^18,43,53 and recorded the average intensities of different patterns in Table 1. After that, we did a control experiment in which all the devices were the same as the previous one except for the modulator was replaced by a commercial LiNbO₃ MZI. In the control experiment, we also prepared random sequences consisting of the three states, and we adjusted the voltage to tune the ${\mathcal{R}}$ to do a comparison with the DPMZI. The comparison is listed in Table 2. The results indicate that under the same condition, the patterning effect in our method is two or three orders of magnitude smaller than the traditional intensity modulator. Employing our modulator is the inevitable demand for higher performance since in practical systems.

Fig. 5: The figure illustrates the output intensity and its partial derivatives.

The upper surface plot illustrates and the two contour plots denote the two partial derivatives. The upper color bar belongs to the surface plot and the lower color bar belongs to the two contour plots. The ‘S’, ‘D’, and ‘V’ points are employed as the signal state, decoy state, and vacuum state respectively and the partial derivatives of the three points are all 0.

Table 1 Patterning effect test.

Table 2 Comparing the MZI and MMZI.

Simulation

Except for the patterning effect, the random intensity fluctuation due to thermal noise or timing jitter of modulation signal also brings side-channels to practical systems. As discussed in previous works^22,26,27,54, considering the worst case in the parameter estimation is a countermeasure for the loophole, but the system performance would be unavoidably reduced and the performance depends on the magnitude of the fluctuation. The MMZI can mitigate the random intensity fluctuation from the modulation signal so that the system performance could be improved. Here we demonstrate the MMZI by extending the intensity fluctuation to ref. ¹³, which is a three-intensity BB84 protocol with a finite-key analysis. (We emphasize that we only analyze the random intensity fluctuation in the simulation since the quantitative theoretical analysis against the correlated intensity fluctuation is still missing at present.).

The protocol definition is same with ref. ¹³, except that the worst case of the mean photon number in the range of $[{\mu }_{a}^{L},{\mu }_{a}^{U}]$ (a ∈ {s,d, v}) is considered in the parameter estimation. The secret key is extracted from the events whereby Alice and Bob both choose the X basis. The intensities are denoted by μ_s, μ_d and μ_v, respectively, and they satisfy μ_s > μ_d + μ_v and μ_d > μ_v≥0. The intensities are selected with probabilties ${p}_{{\mu }_{s}}$, ${p}_{{\mu }_{d}}$ and ${p}_{{\mu }_{v}}$, respectively. In the scenario that the random intensity fluctuation and finite-key effect are considered, the parameters estimation of decoy state method should be modified. The lower-bound on the number of vacuum events s_b,0 in basis b (b ∈ {X, Z}) is estimated by:

$$\begin{array}{ll}&{s}_{b,0}^{L}=\min :{\tau }_{0}({\mu }_{s},{\mu }_{d},{\mu }_{v})\frac{{\mu }_{d}{F}^{-}({n}_{b}^{v},{\mu }_{v})-{\mu }_{v}{F}^{+}({n}_{b}^{d},{\mu }_{d})}{{\mu }_{d}-{\mu }_{v}},\\ &s.t.\,\,{\mu }_{a}^{L}\le {\mu }_{a}\le {\mu }_{a}^{U},\\ &{\rm{for}}\ a\in \{s,d,v\},\end{array}$$

(11)

where n_b,a denotes the event number when Alice select basis b and intensity μ_a, the ${\tau }_{0}({\mu }_{s},{\mu }_{d},{\mu }_{v})={e}^{-{\mu }_{s}}{p}_{{\mu }_{s}}+{e}^{-{\mu }_{d}}{p}_{{\mu }_{d}}+{e}^{-{\mu }_{v}}{p}_{{\mu }_{v}}$ is the probability that Alice sends a 0-photon state and the

$${F}^{\pm }({n}_{b}^{a},{\mu }_{a})=\frac{{e}^{{\mu }_{a}}}{{p}_{{\mu }_{a}}}\left[{n}_{b}^{a}\pm \sqrt{{n}_{b}{\mathrm{ln}}\,\frac{21}{{\epsilon }_{\rm{sec}}}}\right].$$

(12)

is an intermediate variable corresponding to the Hoeffding’s inequality.

In addition, the lower-bound on the number of single-photon events s_b,1 in basis b (b ∈ {X, Z}) is estimated by:

$$\begin{array}{l}{s}_{b,1}^{L}=\min :\frac{{\tau }_{1}({\mu }_{s},{\mu }_{d},{\mu }_{v}){\mu }_{s}}{{\mu }_{s}({\mu }_{d}-{\mu }_{v})-{\mu }_{d}^{2}+{\mu }_{v}^{2}}\times \left[\right.{F}^{-}({n}_{b}^{d},{\mu }_{d})-{F}^{+}({n}_{b}^{v},{\mu }_{v})\\ \,\qquad\quad-\frac{{\mu }_{d}^{2}-{\mu }_{v}^{2}}{{\mu }_{s}^{2}}({F}^{+}({n}_{b}^{s},{\mu }_{s})-\frac{{s}_{b,0}^{L}}{{\tau }_{0}({\mu }_{s},{\mu }_{d},{\mu }_{v})})\left]\right.,\\ \,\qquad\quad s.t.\,\,{\mu }_{a}^{L}\le {\mu }_{a}\le {\mu }_{a}^{U},\\ \,\qquad\quad{\rm{for}}\ a\in \{s,d,v\},\end{array}$$

(13)

where the ${\tau }_{1}({\mu }_{s},{\mu }_{d},{\mu }_{v})={e}^{-{\mu }_{s}}{\mu }_{s}{p}_{{\mu }_{s}}+{e}^{-{\mu }_{d}}{\mu }_{d}{p}_{{\mu }_{d}}+{e}^{-{\mu }_{v}}{\mu }_{v}{p}_{{\mu }_{v}}$ is the probability that Alice sends a single-photon state.

After that, the upper-bound of the number of bit errors associated with the single-photon events in Z-basis ν_Z,1 is modified as:

$$\begin{array}{ll}&{\nu }_{Z,1}^{U}=\max :{\tau }_{1}({\mu }_{s},{\mu }_{d},{\mu }_{v})\frac{{F}^{+}({m}_{Z}^{d},{\mu }_{d})-{F}^{-}({m}_{Z}^{v},{\mu }_{v})}{{\mu }_{d}-{\mu }_{v}},\\ &s.t.\,\,{\mu }_{a}^{L}\le {\mu }_{a}\le {\mu }_{a}^{U},\\ &{\rm{for}}\ a\in \{s,d,v\},\end{array}$$

(14)

where the ${m}_{Z}^{a}$ denotes the number of bit errors when Alice selects Z-basis and intensity μ_a.

With the modified formulas of the three-intensity decoy-state method, we can estimate a secret key rate when the random intensity fluctuation exists. Here simulate the BB84 protocol with random intensity fluctuation, and compare the system performance between employing commercial MZI and MMZI. The protocol definition and the formulas are same with ref. ¹³ except for the formulas of the decoy-state method are replaced by Eqs. (11), (13), and (14), in which the intensity fluctuation $[{\mu }_{a}^{L},{\mu }_{a}^{U}]$ is considered. The difference between employing commercial MZI and the DPMZI is that the fluctuation is different. Since the electronic noise, when Alice wants to a voltage corresponding to the relative phase α, she actually loads a random voltage in a range which corresponds to the relative phase in the range of $\left[{\alpha }^{L},{\alpha }^{U}\right]$. When a commercial MZI is employed, the intensity fluctuation is

$$\begin{array}{ll}&{\mu ^{\prime} }_{a}^{L}=\min :\frac{{\mu }_{\rm{in}}}{2}(1+\cos ({\alpha }_{a})),\\ &{\mu ^{\prime} }_{a}^{U}=\max :\frac{{\mu }_{\rm{in}}}{2}(1+\cos ({\alpha }_{a})),\\ &s.t.{\alpha }_{a}\in \left[{\alpha }_{a}^{L},{\alpha }_{a}^{U}\right],\end{array}$$

(15)

where a ∈ {s, d, v} and the α_a denotes the corresponding relative phase for intensity ${\mu ^{\prime} }_{a}$. Similarly, when the MMZI (we take the DPMZI as an example) is employed, the intensity fluctuation is

$$\begin{array}{l}{\mu ^{\prime} }_{a}^{L}=\min :\frac{{\mu }_{\rm{in}}}{4}\left[\eta +\sqrt{\eta }(\cos {\alpha }_{1,a}+\cos {\alpha }_{2,a})\right.\\ \quad\qquad\left.+\frac{1}{2}+\frac{1}{2}\cos ({\alpha }_{1,a}-{\alpha }_{2,a})\right]\\ \qquad=0,{\mu ^{\prime} }_{a}^{U}=\max :\frac{{\mu }_{\rm{in}}}{4}\left[\eta +\sqrt{\eta }(\cos {\alpha }_{1,a}+\cos {\alpha }_{2,a})\right.\\ \quad\qquad\left.+\frac{1}{2}+\frac{1}{2}\cos ({\alpha }_{1,a}-{\alpha }_{2,a})\right]\\ \qquad=0,\,s.t.\,\,{\alpha }_{1,a}\in \left[{\alpha }_{1,a}^{L},{\alpha }_{1,a}^{U}\right],\,\,{\alpha }_{2,a}\in \left[{\alpha }_{2,a}^{L},{\alpha }_{2,a}^{U}\right],\end{array}$$

(16)

where the α_1,a and α_2,a are corresponding relative phases for intensity μ_a and the η should be tuned to be 0.6545 to make μ_d = 0.2μ_s. We further assume that the source has a fluctuation of δ_I, the output μ_a is in the range of $\left[{\mu }_{a}^{L},{\mu }_{a}^{U}\right]$, where

$$\begin{array}{ll}&{\mu }_{a}^{L}=\min ({\mu ^{\prime} }_{a}^{L}(1-{\delta }_{I}),1{0}^{-3}{\mu }_{s}),\\ &{\mu }_{a}^{U}={\mu ^{\prime} }_{a}^{U}(1+{\delta }_{I}),\end{array}$$

(17)

where the 10⁻³ is the extinction ratio of the modulator.

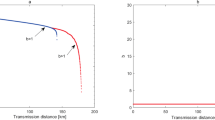
Here, we compare the difference of intensity fluctuation and secret key rate between employing commercial MZI and MMZI. In our simulation, the detection efficiency is 10%, the dark count rate is 6 × 10⁻⁷, the after-pulse probability is 4 × 10⁻², the misalignment error rate is 5 × 10⁻³, and the fluctuation of the laser source δ_I = 1%. The security parameters for finite-key effect are all same with ref. ¹³ and the block size n_X is fixed to 10⁷. The probabilities ${p}_{{\mu }_{s}}=0.7$, ${p}_{{\mu }_{d}}=0.2$, and ${p}_{{\mu }_{v}}=0.1$. The probability of selecting X basis is 0.61. We fix the intensities to μ_s = 0.44, μ_d = 0.2μ_s = 0.088, μ_v = 10⁻³μ_s. The intensity fluctuations are listed in Table 3 and the secret key rates are showed in Fig. 7. The simulation results indicate that the MMZI mitigates the random intensity fluctuation and significantly improves the system performance. When the phase deviation is π/20, the system with DPMZI is nearly ideal while the system with MZI is nearly broken.

Table 3 Intensity fluctuation.

Fig. 6: Oscilloscope traces: a random sequence including μ_s, μ_d, μ_v.

The figure shows part of the recorded data.

Fig. 7: The secret key rate as the function of communication distance in the scenario that the random intensity fluctuation is considered.

The black-dot line denotes the ideal key rate without any intensity fluctuation. The red, yellow, and blue lines denote the maximum phase deviation δ_α is π/40, π/30, and π/20, respectively. The modulated phase is in the range of [α − δ_α, α + δ_α]. The solid line and dash line denote employing MMZI and MZI, respectively.