Introduction

In 1991, Peres and Wootters proposed a seminal problem1: What is the difference between global and local measurements on quantum states prepared at different locations? The question naturally leads to an investigation into the role of local operations and classical communication (LOCC), which is necessary for characterizing entanglement2 and the nonlocality of quantum information3,4,5,6,7,8,9,10,11,12,13,14,15. Because the global measurement is to measure quantum states at different locations as a whole, it can be entangled or not. When it is not entangled, it is called a separable measurement (SEP). In other words, SEP is a measurement consisting of separable operators. A local measurement is to measure locally quantum states at different locations. A local measurement is performed at one location, and the result is sent to the other location to perform a suitable measurement. And LOCC can be finite or infinite16. Every LOCC can be realized through SEP, but the inverse does not hold3.

To understand the role of LOCC, Peres and Wootters considered the minimum-error discrimination (MD)17,18,19,20 of double trine ensemble and showed that there is a difference between a global measurement and finite rounds of local measurements on the quantum ensemble1. Also, Bennett et al.3 showed that nine orthogonal product states could provide “nonlocality without entanglement” (NLWE) because it is impossible to distinguish the nine states by asymptotic LOCC21,22 even though they can be distinguished globally. One should note that the nonlocality does not mean the nonlocality of quantum state, but the nonlocality of quantum ensemble composing the quantum state. Their investigation provides a motivation by which researchers have performed on discrimination of multipartite states under restricted quantum operations of LOCC or SEP4,5,6,7,8,9,10,11,12,13,14,15,16,21,22,23,24,25,26.

Recently, Chitambar and Hsieh15 showed that in terms of MD, NLWE occurs in double trine ensemble1, which consists of three symmetric 2 ⊗ 2 product states with identical prior probability. More explicitly, it means that in MD of double trine ensemble the guessing probability of globally optimal measurement is larger than that of asymptotic LOCC (\(\overline{{\rm{LOCC}}}\)). The result shows a specific quantum ensemble revealing NLWE when they are shared at different locations, but it cannot tell whether NLWE depends on the manner of forming a quantum ensemble. Then, the following three questions naturally appear. The first one is whether there exists a nonorthogonal state ensemble revealing NLWE as double trine ensemble shows NLWE. The second one is whether one can show NLWE of nonorthogonal state ensemble by appealing SEP, which one can handle more easily than \(\overline{{\rm{LOCC}}}\). The last and most important question is whether an explicit dependence on prior probabilities in terms of MD can be shown in NLWE. In other words, one can ask whether there exist nonorthogonal states whose NLWE depends on nonzero prior probabilities. To the best of the authors’ knowledge, an answer to this question has not yet been offered.

In this work, we provide three nonorthogonal product states in a two-qubit system where the occurrence of NLWE depends on nonzero prior probabilities. The ensemble’s quantum states do not carry a cyclic symmetry as the three states of the double trine ensemble do. However, they possess a mirror symmetry. Using the three quantum states with two different parametrizations, we show that there are the following two instances for nonzero prior probabilities. The one is the case where global minimum-error measurement can be performed only by finite-round LOCC. The other one is that SEP cannot achieve global minimum-error measurement. In the former case, NLWE does not occur, but in the latter case, NLWE does occur. Therefore, our results provide answers to the three questions mentioned previously.

Results

The difficulty in understanding the explicit dependence of prior probability in NLWE is due to the fact that a general method to obtain an optimal measurement for three quantum states is not known yet. Therefore, one should consider a suitable quantum ensemble where one can find its optimal measurement and further can discuss the optimality of local measurement.

Case where different quantum states are shared at different locations

Now, we begin our investigation by considering the case where different quantum states are shared at different locations. The quantum ensemble is given as \({\mathcal{E}}={\{{q}_{i},{\rho }_{i}\}}_{i = 0}^{2}\), and consists of two-qubit product states \({\rho }_{i}=\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\) with prior probabilities qi. It satisfies the following relation:

$$\frac{{q}_{0}}{{q}_{1}}=\frac{{q}_{0}}{{q}_{2}}=r\, \,{\mathrm{for}}\;{\mathrm{some}}\,\, r\in (0,\infty ).$$
(1)

The ratio r is the only variable indicating the change of prior probabilities. The two-qubit product states \(\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\), which we consider, are as follows (the ranges of θ0 and θ1 become \(0\;<\;{\theta }_{0}\;<\;\frac{\pi }{4}\) and \(0\;<\;{\theta }_{1}\;<\;\frac{\pi }{2}-{\theta }_{0}\)):

$$\begin{array}{l}\left|{{{\Psi }}}_{0}\right\rangle \,=\,\left|00\right\rangle ,\\ \left|{{{\Psi }}}_{1}\right\rangle \,=\,\left|{A}_{+}\right\rangle \otimes \left|{B}_{+}\right\rangle \\ \quad\quad\,\,=\,\sqrt{\frac{\sin \,2{\theta }_{0}}{\sin\, 2{\theta }_{0}+\sin \,2{\theta }_{1}}}\left|{{{\Phi }}}_{{\theta }_{1}}^{+}\right\rangle +\sqrt{\frac{\sin \,2{\theta }_{1}}{\sin \,2{\theta }_{0}+\sin \,2{\theta }_{1}}}\left|{{{\Psi }}}_{{\theta }_{0}}^{+}\right\rangle ,\quad \\ \left|{{{\Psi }}}_{2}\right\rangle \,=\,\left|{A}_{-}\right\rangle \otimes \left|{B}_{-}\right\rangle \\ \quad\quad\,\,=\,\sqrt{\frac{\sin \,2{\theta }_{0}}{\sin \,2{\theta }_{0}+\sin \,2{\theta }_{1}}}\left|{{{\Phi }}}_{{\theta }_{1}}^{+}\right\rangle -\sqrt{\frac{\sin \,2{\theta }_{1}}{\sin \,2{\theta }_{0}+\sin \,2{\theta }_{1}}}\left|{{{\Psi }}}_{{\theta }_{0}}^{+}\right\rangle ,\end{array}$$
(2)

where

$$\begin{array}{lll}\left|{A}_{\pm }\right\rangle &=&\frac{1}{\sqrt{1+\tan \,{\theta }_{0}\tan\, {\theta }_{1}}}(\left|0\right\rangle \pm \sqrt{\tan \,{\theta }_{0}\tan \,{\theta }_{1}}\left|1\right\rangle ),\\ \left|{B}_{\pm }\right\rangle &=&\frac{1}{\sqrt{\tan\, {\theta }_{0}+\tan {\theta }_{1}}}(\sqrt{\tan \,{\theta }_{0}}\left|0\right\rangle \pm \sqrt{\tan\, {\theta }_{1}}\left|1\right\rangle ),\end{array}$$

and

$$\begin{array}{lll}\left|{{{\Phi }}}_{\theta }^{+}\right\rangle &=&\cos\, \theta \left|00\right\rangle +\sin \,\theta \left|11\right\rangle ,\ \left|{{{\Phi }}}_{\theta }^{-}\right\rangle =\sin \,\theta \left|00\right\rangle -\cos\, \theta \left|11\right\rangle ,\\ \left|{{{\Psi }}}_{\theta }^{+}\right\rangle &=&\cos \,\theta \left|01\right\rangle +\sin \,\theta \left|10\right\rangle ,\ \left|{{{\Psi }}}_{\theta }^{-}\right\rangle =\sin\, \theta \left|01\right\rangle -\cos \,\theta \left|10\right\rangle .\end{array}$$

To understand NLWE for this quantum ensemble, we should compare \({P}_{{\rm{guess}}}^{{\rm{GLOBAL}}}\), the guessing probability when the global measurement is used, with \({P}_{{\rm{guess}}}^{\overline{{\rm{LOCC}}}}\), when only local measurements are allowed. The optimal positive operator-valued measure (POVM) \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) for \({\mathcal{E}}\) can be described in three-dimensional complex Hilbert space generated by \({\{\left|{{{\Psi }}}_{i}\right\rangle \}}_{i = 0}^{2}\) (see “Methods”):

$$\begin{array}{l}\left|{{{\Phi }}}_{0}\right\rangle \,=\,\sin\,\chi \left|00\right\rangle -\cos \,\chi \left|11\right\rangle ,\\ \left|{{{\Phi }}}_{1}\right\rangle \,=\,\frac{1}{\sqrt{2}}(\cos \,\chi \left|00\right\rangle +\sin \,\chi \left|11\right\rangle )+\frac{1}{\sqrt{2}}\left|{{{\Psi }}}_{{\theta }_{0}}^{+}\right\rangle ,\\ \left|{{{\Phi }}}_{2}\right\rangle \,=\,\frac{1}{\sqrt{2}}(\cos \,\chi \left|00\right\rangle +\sin \,\chi \left|11\right\rangle )-\frac{1}{\sqrt{2}}\left|{{{\Psi }}}_{{\theta }_{0}}^{+}\right\rangle ,\end{array}$$
(3)

where the optimal measurement factor \(\chi \in (0,\frac{\pi }{2})\) satisfies the following relation:

$$r=\frac{\sin \,2{\theta }_{0}\sin \,2(\chi -{\theta }_{1})+2\sqrt{\sin\, 2{\theta }_{0}\sin\, 2{\theta }_{1}}\sin\, (\chi -{\theta }_{1})}{\sin \,2\chi (\sin\, 2{\theta }_{0}+\sin\, 2{\theta }_{1})}.\quad$$
(4)

The global guessing probability \({P}_{{\rm{guess}}}^{{\rm{GLOBAL}}}\) of the quantum ensemble \({\mathcal{E}}\) can be obtained by applying the optimal global measurement. To figure out NLWE, one needs to check whether the global minimum-error probability can be obtained by the finite-round LOCC or asymptotic LOCC21,22. It is known that the global minimum-error probability can be attained by finite-round (asymptotic) LOCC if and only if the optimal POVM \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) can be perfectly discriminated using the finite-round (asymptotic) LOCC (see “Methods”). Here, in understanding this problem, one can recall a result obtained by Walgate and Hardy5. It tells that in a two-qubit system, three pure orthogonal states can be perfectly discriminated by a finite-round LOCC if and only if at least two of them are product states. It means that \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) can be perfectly discriminated by a finite-round LOCC if and only if at least two of \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) are product states. Therefore, the possibility of NLWE depends on whether \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) is entangled or not. By evaluating concurrence27, one can see that two of the \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) become unentangled if and only if \(\sin \,2\chi =\sin \,2{\theta }_{0}\) (i.e., χ = θ0 or \(\frac{\pi }{2}-{\theta }_{0}\)). Then, the necessary and sufficient condition for the finite-round LOCC to achieve globally optimal discrimination (\({{\rm{LOCC}}}_{{\Bbb{N}}}={\rm{GLOBAL}}\)) is determined by \({\gamma }_{-}\;{\mathrm{or}}\;{\gamma }_{+}\):

$$\begin{array}{lll}{\gamma }_{-}&=&\frac{\sin\, 2({\theta }_{0}-{\theta }_{1})\sqrt{\sin \,2{\theta }_{0}}+2\sin \,({\theta }_{0}-{\theta }_{1})\sqrt{\sin\, 2{\theta }_{1}}}{(\sin\, 2{\theta }_{0}+\sin \,2{\theta }_{1})\sqrt{\sin\, 2{\theta }_{0}}},\\ {\gamma }_{+}&=&\frac{\sin\, 2({\theta }_{0}+{\theta }_{1})\sqrt{\sin\, 2{\theta }_{0}}+2\cos\, ({\theta }_{0}+{\theta }_{1})\sqrt{\sin \,2{\theta }_{1}}}{(\sin \,2{\theta }_{0}+\sin\, 2{\theta }_{1})\sqrt{\sin\, 2{\theta }_{0}}},\end{array}$$
(5)

where γ− and γ+ are the ratios that correspond to the cases of χ = θ0 and \(\chi =\frac{\pi }{2}-{\theta }_{0}\), respectively. That is, NLWE does not occur if r is γ− or γ+. γ−(γ+) becomes positive when θ1 < θ0(\({\theta }_{1}<\frac{\pi }{2}-{\theta }_{0}\)). Therefore, for the mirror-symmetric states of Eq. (2), there is at least one set of nonzero prior probabilities in which NLWE does not occur. Note that when \({\theta }_{0}\,\ne\,\frac{\pi }{4}\), there is a finite gap \({\mathcal{G}}\) between γ− and γ+:

$${\mathcal{G}}=\{x\in {\mathbb{R}}\,| \,{\gamma }_{-}\;<\; {x}\,<\,{\gamma }_{+}\}.$$
(6)

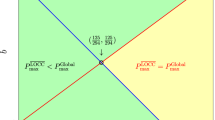
Until now, we have studied the possibility that a finite-round LOCC can achieve the global minimum-error probability of \({\mathcal{E}}\). Since an SEP can perform better than a finite-round LOCC in MD, now we will investigate a case that an SEP can obtain the global guessing probability \({P}_{{\rm{guess}}}^{{\rm{GLOBAL}}}\) of \({\mathcal{E}}\). If we state the result in advance, as shown in Figure 1, when \(r\,\notin\, {\mathcal{G}}\) (yellow), the global minimum-error probability of the quantum ensemble \({\mathcal{E}}\) can be achieved through an SEP. However, when \(r\in {\mathcal{G}}\) (green), the global minimum-error probability of a quantum state ensemble \({\mathcal{E}}\) cannot be obtained by an SEP. This is obtained by applying the result of Duan et al.11 (see “Methods”) to an orthonormal basis \(\{\left|{{{\Phi }}}_{0}\right\rangle ,\left|{{{\Phi }}}_{1}\right\rangle ,\left|{{{\Phi }}}_{2}\right\rangle ,\left|{{{\Psi }}}_{{\theta }_{0}}^{-}\right\rangle \}\); the necessary and sufficient condition that SEPs can perform the perfect discrimination of \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) becomes \(\sin\,2\chi \le \sin \,2{\theta }_{0}\), which can be rewritten as \(\chi \,\notin\, ({\theta }_{0},\frac{\pi }{2}-{\theta }_{0})\). For \(0\,<\,{\chi}\, <\,\frac{\pi }{2}\), the rate r strictly increases as a function of χ. Therefore, \(r\;\notin\; {\mathcal{G}}\) becomes the necessary and sufficient condition for r, when globally optimal discrimination of \({\mathcal{E}}\) can be achieved by an SEP: SEP = GLOBAL. One obtains \(r\;\in\; {\mathcal{G}}\) if and only if the global minimum-error probability of \({\mathcal{E}}\) cannot be accomplished by an SEP: SEP < GLOBAL. Therefore, two singular rates γ− and γ+ form a boundary between SEP = GLOBAL and SEP < GLOBAL. Figure 1 displays the behavior of two rates γ− and γ+ when \({\theta }_{0}\,\ne \,\frac{\pi }{4}\). Because SEP < GLOBAL includes \(\overline{{\rm{LOCC}}}<{\rm{GLOBAL}}\), when r belongs to \({\mathcal{G}}\), the NLWE occurs, i.e., \({P}_{{\rm{guess}}}^{\overline{{\rm{LOCC}}}}\,<\,{P}_{{\rm{guess}}}^{{\rm{GLOBAL}}}\). This means that, for the mirror-symmetric states of Eq. (2), there are infinite numbers of sets of nonzero prior probabilities revealing NLWE.

Fig. 1: Appearance of NLWE.
figure 1

When \({\theta }_{0}\,\ne \,\frac{\pi }{4}\), if θ1 < θ0, both singular rates γ− and γ+ are valid. However, when \({\theta }_{1}\ge \frac{\pi }{2}-{\theta }_{0}\), both γ− and γ+ are not valid. If \({\theta }_{0}\le {\theta }_{1}<\frac{\pi }{2}-{\theta }_{0}\), γ+ is valid but γ− is not. When the ratio r becomes γ− (blue) or γ+ (red), the global minimum-error probability of a quantum ensemble \({\mathcal{E}}\) can be achieved by a finite-round LOCC, otherwise it cannot be obtained by finite-round LOCC. Furthermore, if \(r\,\notin \,{\mathcal{G}}\) (yellow), the global minimum-error probability of the quantum ensemble \({\mathcal{E}}\) can be achieved by means of a separable measurement. Meanwhile, when \(r\;\in \;{\mathcal{G}}\) (green), the global minimum-error probability of a quantum state ensemble \({\mathcal{E}}\) cannot be obtained by a separable measurement.

Full size image

Our results speak of the following fact. When three product states \({\{\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\}}_{i = 0}^{2}\) are specified, corresponding to fixed θ1 and θ0, NLWE depends on nonzero prior probabilities. For the mirror-symmetric states of Eq. (2), there are infinite numbers of sets of nonzero prior probabilities where NLWE occurs (SEP < GLOBAL) and there is at least one set of nonzero prior probabilities in which NLWE does not occur (LOCC\({}_{{\Bbb{N}}}=\)GLOBAL). It tells that those different ensembles, which correspond to different prior probabilities, although composed of the same separable quantum states, exhibit different behaviors in terms of nonlocality. The following theorem summarizes the result.

Theorem 1 For the MD of nonorthogonal states given as Eq. (2), the NLWE explicitly depends on the prior probabilities.

For example, let us consider the case of \({\theta }_{1}={\theta }_{0}\,\ne \,\frac{\pi }{4}\). Then, \(\left|{A}_{\pm }\right\rangle\) and \(\left|{B}_{\pm }\right\rangle\) consisting of \(\left|{{{\Psi }}}_{1}\right\rangle\) and \(\left|{{{\Psi }}}_{2}\right\rangle\) become

$$\left|{A}_{\pm }\right\rangle =\cos\, {\theta }_{0}\left|0\right\rangle \pm \sin \,{\theta }_{0}\left|1\right\rangle \ \;\text{and}\;\ \left|{B}_{\pm }\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle \pm \left|1\right\rangle ).$$
(7)

In this case, since γ− is zero, the necessary and sufficient condition of SEP < GLOBAL is

$$0\,<\, {r}\,<\,{\gamma }_{+}=\cos \,2{\theta }_{0}+\frac{\cos \,2{\theta }_{0}}{\sin \,2{\theta }_{0}}$$
(8)

and the one of \({{\rm{LOCC}}}_{{\Bbb{N}}}={\rm{GLOBAL}}\) is r = γ+. Therefore, NLWE occurs if r < γ+ but not if r = γ+. Figure 2 illustrates in detail how NLWE can occur by different mixing of quantum states in the case of \({\theta }_{1}={\theta }_{0}\;\ne \;\frac{\pi }{4}\).

Fig. 2: NLWE in the case of \({\theta }_{1}={\theta }_{0}\,\ne \,\frac{\pi }{4}\).
figure 2

In two-qubit system, a party R prepares N0 number of quantum state \(\left|{{{\Psi }}}_{0}\right\rangle\) (red), N1 number of quantum state \(\left|{{{\Psi }}}_{1}\right\rangle\) (green), and N1 number of quantum state \(\left|{{{\Psi }}}_{2}\right\rangle\) (yellow). R combines N0 + 2N1 quantum systems and randomly chooses one out of them. Then, the prior probability q1 of quantum state \(\left|{{{\Psi }}}_{1}\right\rangle\) is equal to the prior probability q2 of quantum state \(\left|{{{\Psi }}}_{2}\right\rangle\). The ratio r between the prior probability q0 of quantum state \(\left|{{{\Psi }}}_{0}\right\rangle\) and the prior probability q1 is N0/N1. After the preparation, R sends each qubit to A and B, respectively. When 0 < r < γ+ is satisfied, NLWE occurs in the view of MD, but if r = γ+, NLWE does not occur. More explicitly, because γ+ becomes 343/600 when θ0 satisfies \(\sin\,{\theta }_{0}=3/5\), if N1 = 600, NLWE does not occur when N0 is 343. However, NLWE occurs in the case of N0 = 1, 2, … , 342.

Full size image

Case where identical quantum states are shared at different locations

Now, we are ready to investigate the case where identical quantum states are shared in different locations. It corresponds to the case when \({\theta }_{0}=\frac{\pi }{4}\) in Eq. (2). We will prove that even in this case, NLWE occurs and depends on the prior probability of the quantum ensemble. In this case, \({\{\left|{{{\Psi }}}_{i}\right\rangle \}}_{i = 0}^{2}\) can be rewritten as (the range of ϵ becomes \(0\,<\,\epsilon \,<\,\frac{\pi }{4}\)):

$$\begin{array}{l}\left|{{{\Psi }}}_{0}\right\rangle \,=\,\left|00\right\rangle ,\\ \left|{{{\Psi }}}_{1}\right\rangle \,=\,\left|{D}_{+}\right\rangle \otimes \left|{D}_{+}\right\rangle \\ \quad\quad\,\,=\,{\cos }^{2}\,\epsilon \left|00\right\rangle +{\sin }^{2}\,\epsilon \left|11\right\rangle +\sqrt{2}\cos \,\epsilon \sin\, \epsilon \left|{{{\Psi }}}_{\frac{\pi }{4}}^{+}\right\rangle ,\quad \\ \left|{{{\Psi }}}_{2}\right\rangle \,=\,\left|{D}_{-}\right\rangle \otimes \left|{D}_{-}\right\rangle \\ \quad\quad\,\,=\,{\cos }^{2}\,\epsilon \left|00\right\rangle +{\sin }^{2}\,\epsilon \left|11\right\rangle -\sqrt{2}\cos\,\epsilon \sin \,\epsilon \left|{{{\Psi }}}_{\frac{\pi }{4}}^{+}\right\rangle ,\end{array}$$
(9)

where

$$\left|{D}_{\pm }\right\rangle =\cos\,\epsilon \left|0\right\rangle \pm \sin\,\epsilon \left|1\right\rangle .$$

For the quantum ensemble given as \({\mathcal{E}}={\{{q}_{i},{\rho }_{i}\}}_{i = 0}^{2}\) consisting of above two-qubit product states \({\rho }_{i}=\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\) with prior probabilities qi, one can find the optimal measurement vectors \({\{\left|{{{\Phi }}}_{i}\right\rangle \}}_{i = 0}^{2}\), which corresponds to the optimal measurement of Eq. (3) at \({\theta }_{0}=\frac{\pi }{4}\). The optimal measurement factor \(\chi \in (0,\frac{\pi }{2})\) satisfies the following relation:

$$\begin{array}{ll}r\,=\,\frac{1}{\sin\,2\chi }\left[\sin\,2\chi \,\cos\,2\epsilon -\frac{1}{2}\cos\,2\chi \,{\sin }^{2}\,2\epsilon \right.\\ \qquad\,\left.+\sqrt{2}\sin\, 2\epsilon (\sin\, \chi \,{\cos }^{2}\,\epsilon -\cos\, \chi\, {\sin }^{2}\,\epsilon )\right].\end{array}$$
(10)

By the similar analysis as before, one can see that \(\left|{{{\Phi }}}_{1}\right\rangle\) and \(\left|{{{\Phi }}}_{2}\right\rangle\) are entangled except in the case of \(\chi =\frac{\pi }{4}\). In other words, one can obtain \(\chi =\frac{\pi }{4}\) if and only if at least two of \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) are product states. If one applies \(\chi =\frac{\pi }{4}\) to the right-hand side of (10), the ratio r can be expressed as \({\gamma }_{0}^{\circ }\):

$${\gamma }_{0}^{\circ }=\cos \,2\epsilon (1+\sin\, 2\epsilon ).$$
(11)

That is, χ becomes \(\frac{\pi }{4}\) if and only if \(r={\gamma }_{0}^{\circ }\). It should be noted that when \(\frac{\pi }{4}\,\le\, \epsilon \,<\,\frac{\pi }{2}\), \(r={\gamma }_{0}^{\circ }\) is not satisfied because \({\gamma }_{0}^{\circ }\) is non-positive. Therefore, one has \(r={\gamma }_{0}^{\circ }\) if and only if the global minimum-error probability of \({\{{q}_{i},\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\}}_{i = 0}^{2}\) can be achieved by a finite-round LOCC: \({{\rm{LOCC}}}_{{\Bbb{N}}}={\rm{GLOBAL}}\). This means that, for the mirror-symmetric states of Eq. (9), there is at least one set of nonzero prior probabilities where NLWE does not occur.

In order to find a case where an asymptotic LOCC cannot provide the global minimum-error probability, one may consult the result by Chitambar and Hsieh15, which states that \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) of the double trine ensemble (\(\epsilon =\frac{\pi }{3}\), r = 1) cannot fulfill the necessary condition of perfect asymptotic LOCC discrimination21. Therefore, for all quantum ensemble \({\mathcal{E}}\) with \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\) corresponding to \((\epsilon ,r)=(\frac{\pi }{3},1)\), an asymptotic LOCC cannot provide the global guessing probability, i.e., \({P}_{{\rm{guess}}}^{\overline{{\rm{LOCC}}}}\,<\,{P}_{{\rm{guess}}}^{{\rm{GLOBAL}}}\). Because the value of χ, derived from Eq. (10) with r = 1 and \(\epsilon =\frac{\pi }{3}\), satisfies \(\sin\,\chi =(\sqrt{2}+1)/\sqrt{6}\), \({\{\left|{{{\Lambda }}}_{i}^{+}\right\rangle \ \left\langle {{{\Lambda }}}_{i}^{+}\right|\}}_{i = 0}^{2}\) cannot be perfectly discriminated by asymptotic LOCC, where

$$\begin{array}{l}\left|{{{\Lambda }}}_{0}^{\pm }\right\rangle \,=\,\frac{\sqrt{2}\pm 1}{\sqrt{6}}\left|00\right\rangle -\frac{\sqrt{2}\mp 1}{\sqrt{6}}\left|11\right\rangle ,\\ \left|{{{\Lambda }}}_{1}^{\pm }\right\rangle \,=\,\frac{1}{\sqrt{2}}(\frac{\sqrt{2}\mp 1}{\sqrt{6}}\left|00\right\rangle +\frac{\sqrt{2}\pm 1}{\sqrt{6}}\left|11\right\rangle )+\frac{1}{\sqrt{2}}\left|{{{\Psi }}}_{\frac{\pi }{4}}^{+}\right\rangle ,\\ \left|{{{\Lambda }}}_{2}^{\pm }\right\rangle \,=\,\frac{1}{\sqrt{2}}(\frac{\sqrt{2}\mp 1}{\sqrt{6}}\left|00\right\rangle +\frac{\sqrt{2}\pm 1}{\sqrt{6}}\left|11\right\rangle )-\frac{1}{\sqrt{2}}\left|{{{\Psi }}}_{\frac{\pi }{4}}^{+}\right\rangle .\end{array}$$

In addition, \({\{\left|{{{\Lambda }}}_{i}^{-}\right\rangle \ \left\langle {{{\Lambda }}}_{i}^{-}\right|\}}_{i = 0}^{2}\) cannot be perfectly discriminated by asymptotic LOCC because \(\left|{{{\Lambda }}}_{i}^{+}\right\rangle \ \left\langle {{{\Lambda }}}_{i}^{+}\right|\) and \(\left|{{{\Lambda }}}_{i}^{-}\right\rangle \ \left\langle {{{\Lambda }}}_{i}^{-}\right|\) can be exchanged by the local unitary operation σX ⊗ σX, where \({\sigma }_{X}=\left|0\right\rangle \left\langle 1\right|+\left|1\right\rangle \left\langle 0\right|\). One should note that \(\left|{{{\Lambda }}}_{i}^{\pm }\right\rangle\) is \(\left|{{{\Phi }}}_{i}\right\rangle\) with χ, which corresponds to \(\sin\,\chi =(\sqrt{2}\pm 1)/\sqrt{6}\). In both of these cases, χ satisfies \(\sin\,\chi =1/3\). Therefore, \({\{\left|{{{\Phi }}}_{i}\right\rangle \ \left\langle {{{\Phi }}}_{i}\right|\}}_{i = 0}^{2}\), when \(\sin\,\chi =1/3\), cannot be perfectly discriminated by asymptotic LOCC. If one applies \(\sin\,\chi =(\sqrt{2}\pm 1)/\sqrt{6}\) to the right-hand side of Eq. (10), the ratio r can be expressed as \({\gamma }_{\pm }^{\circ}\):

$${\gamma }_{\pm }^{\circ }=\cos\,2\epsilon (\sqrt{6}\sin \,2\epsilon +1)\pm \sin \,2\epsilon (\sqrt{2}\sin\, 2\epsilon +\sqrt{3}).$$

Therefore, if \(r={\gamma }_{+}^{\circ }\) or \({\gamma }_{-}^{\circ }\), the global minimum-error probability of \({\{{q}_{i},\left|{{{\Psi }}}_{i}\right\rangle \ \left\langle {{{\Psi }}}_{i}\right|\}}_{i = 0}^{2}\) cannot be achieved by asymptotic LOCC: \(\overline{{\rm{LOCC}}}\,<\,{\rm{GLOBAL}}\). This implies that, for the mirror-symmetric states of Eq. (9), there is at least one set of nonzero prior probabilities in which NLWE occurs.

These results imply the following fact: when three product states are specified that correspond to a fixed ϵ, NLWE depends on nonzero prior probabilities. More explicitly, for the mirror-symmetric states of Eq. (9), there is at least one set of nonzero prior probabilities where NLWE occurs (\(\overline{{\mathrm{LOCC}}}\,<\,{\mathrm{GLOBAL}}\)), and there is a set of nonzero prior probabilities in which NLWE does not occur (\({\mathrm{LOCC}}_{\Bbb{N}}\,=\,{\mathrm{GLOBAL}}\)). The situation is illustrated in Fig, 3, which displays the rates \({\gamma }_{0}^{\circ }\) and \({\gamma }_{\pm }^{\circ }\) corresponding to ϵ. For the curve \({\gamma }_{0}^{\circ }\) shown in Fig. 3, there is no NLWE, but in the other two curves, \({\gamma }_{+}^{\circ }\) and \({\gamma }_{-}^{\circ }\), NLWE occurs. That is, when \(\epsilon\, <\,\frac{\pi }{4}\), NLWE in MD depends on the prior probability, in contrast to the perfect discrimination of orthogonal states. The following theorem summarizes the result.

Fig. 3: Appearance of NLWE in a singular case.
figure 3

\({\gamma}_{0}^{\circ }\) (black), \(\gamma_{+}^{0}\) (red), and \(\gamma_{-}^{0}\) (blue) corresponding to \(\epsilon\in(0,\frac{\pi}{2})\): when \(0\,<\,\epsilon \,<\,\frac{\pi}{4}\), \({\gamma }_{0}^{\circ }\) and \(\gamma_{+}^{\circ}\) are positive. However, when \(\frac{\pi}{4}\,\le\,\epsilon\,<\,\frac{\pi}{2}\), \({\gamma }_{0}^{\circ }\) and \(\gamma_{-}^{\circ}\) are non-positive. Because the ratio r must be positive, when \(0\,<\,\epsilon\, <\,\frac{\pi}{4}\), there are two cases when NLWE occurs and does not. However, when \(\frac{\pi}{4}\,\le \,\epsilon\,<\,\frac{\pi}{2}\), it is impossible to explicitly indicate the occurrence of NLWE. The double trine ensemble corresponds to the case of \(\epsilon=\frac{\pi }{3}\) and r = 1.

Full size image

Theorem 2 For the MD of nonorthogonal states given as Eq. (9), the NLWE explicitly depends on the prior probabilities.

Discussion

In this study, we showed that nonlocality depends on not only separable quantum states of a quantum ensemble but also the prior probabilities of given quantum states. It was proved by showing that nonlocal measurement on the mirror-symmetric quantum ensemble provides more information about the unentangled states than LOCC does when the prior probabilities have special values. Our result implies that nonlocality can be revealed by way of mixing given separable quantum states. In the view that NLWE of orthogonal states does not show explicit dependence on prior probabilities, our result is surprising.

Also, we considered the specific quantum states with a mirror symmetry, which are used to prove that NLWE depends explicitly on the prior probability of the quantum ensemble. We should note that the quantum states are parametrized by variables θ0 and θ1, and there are infinite numbers of quantum states that reveal NLWE.

Here, we provided a new type of quantum ensemble with mirror symmetry. Moreover, by exploiting it, we can provide cases where NLWE can be shown. However, because there are cases where one cannot decide on the occurrence of NLWE, more investigation is needed. Further, it is interesting to know how frequently NLWE can occur. The weakening of mirror symmetry may help to accomplish the investigation.

In our work, we provided an actual result on the explicit dependence of prior probability in the behavior of NLWE. From this point of view, the following needs to be noted. In the perfect discrimination of nine orthogonal states of ref. 3, NLWE occurs regardless of prior probability. Furthermore, since finite-round LOCC can perfectly discriminate pure orthogonal product states (for instance, two multipartite states23, three 2 ⊗ 2 states, and four 2 ⊗ 2 states5), NLWE does not occur regardless of prior probability. In perfect discrimination of orthogonal multipartite states, measurements discriminating perfectly the quantum states are independent of prior probabilities. Therefore, in the cases, NLWE depends only on those quantum states, not on the values of nonzero prior probabilities. It implies that in perfect discrimination of orthogonal multipartite states, one cannot see explicit dependence on prior probabilities. However, in MED of nonorthogonal states, optimal measurements may depend on nonzero prior probabilities. Therefore, in this case, NLWE may rely not only on quantum states but also on prior probabilities. It should be noted that in two bipartite nonorthogonal pure states, LOCC can provide optimal discrimination regardless of prior probabilities24. Therefore, the discrimination of nonorthogonal states does not guarantee the explicit dependence of prior probabilities. It is unknown whether nonorthogonal quantum states can provide NLWE regardless of prior probability in MED. We leave it an open problem. If such a set of nonorthogonal states exists, one can classify NLWE of nonorthogonal states by explicit dependence of prior probabilities.

Now, let us discuss some implications of our results. Our results tell that according to the quantum states in our paper, local optimal discrimination depends explicitly on the variation of prior probability. Since orthogonal states (i.e., local distinguishable states), which can be discriminated by finite-round LOCC, can be applied to quantum data hiding28,29,30,31 and quantum secret sharing32,33,34, our result may be used in extending the result of orthogonal states to the application of nonorthogonal states.

Methods

Mirror-symmetric ensemble

Let us consider quantum state ensemble \({\mathcal{E}}={\{{q}_{i},{\rho }_{i}\}}_{i = 0}^{2}\) consisting of linearly independent pure states \({\rho }_{i}=\left|{\psi }_{i}\right\rangle \ \left\langle {\psi }_{i}\right|\) such that

$$\begin{array}{lll}\left|{\psi }_{0}\right\rangle \,=\,\sin \,\alpha \left|{E}_{0}\right\rangle +\cos \,\alpha \left|{E}_{1}\right\rangle ,\\ \left|{\psi }_{1}\right\rangle \,=\,\sin \,\beta \left|{E}_{1}\right\rangle +\cos \,\beta \left|{E}_{2}\right\rangle ,\\ \left|{\psi }_{2}\right\rangle \,=\,\sin \,\beta \left|{E}_{1}\right\rangle -\cos \,\beta \left|{E}_{2}\right\rangle ,\;0\,<\,\alpha ,\;\beta \,<\,\frac{\pi }{2}.\end{array}$$
(12)

In addition, the prior probabilities q0, q1, and q2 are supposed to be

$$\frac{{q}_{0}}{{q}_{1}}=\frac{{q}_{0}}{{q}_{2}}=r\,\,{\mathrm{for}}\; {\mathrm{some}}\,\,r\in (0,\infty ).$$
(13)

\({\{\left|{E}_{i}\right\rangle \}}_{i = 0}^{2}\) is an orthonormal basis of three-dimensional complex Hilbert space \({\mathcal{H}}\). Note that ρ0 ⊥̸ ρ1 and ρ0 ⊥̸ ρ2, where ⊥̸ indicates nonorthogonality. If U is a unitary operator \(\left|{E}_{0}\right\rangle\left\langle {E}_{0}\right|+\left|{E}_{1}\right\rangle \ \left\langle {E}_{1}\right|-\left|{E}_{2}\right\rangle \left\langle {E}_{2}\right|\), the ensemble \({\mathcal{E}}\) satisfies the following property:

$$U{q}_{0}{\rho }_{0}{U}^{\dagger }={q}_{0}{\rho }_{0},\ U{q}_{1}{\rho }_{1}{U}^{\dagger }={q}_{2}{\rho }_{2},\ U{q}_{2}{\rho }_{2}{U}^{\dagger }={q}_{1}{\rho }_{1}.\qquad$$
(14)

Conversely, when \({\{{q}_{i},{\rho }_{i}\}}_{i = 0}^{2}\) is a quantum ensemble consisting of three linearly independent pure states with ρ0 ⊥̸ ρ1 and ρ0 ⊥̸ ρ2, if there exists a unitary operator U satisfying (14), then the ensemble can be expressed as (12) and (13). Therefore, one can tell that the ensemble \({\mathcal{E}}\) has mirror symmetry.

Until now, the general solution of MD of quantum state ensemble \({\mathcal{E}}\) was unknown. However, a few important results35 was found. First, the minimum-error measurement (the optimal POVM on \({\mathcal{H}}\)) \({\{{M}_{i}\}}_{i = 0}^{2}\) is unique and has a form of a projective measurement composed of orthonormal vectors \(\left|{\phi }_{i}\right\rangle\), which can be expressed by \({M}_{i}=\left|{\phi }_{i}\right\rangle \ \left\langle {\phi }_{i}\right|\). Secondly, for each i, \(\left|{\psi }_{i}\right\rangle\) and \(\left|{\phi }_{i}\right\rangle\) are not perpendicular, \(\left\langle {\psi }_{i}| {\phi }_{i}\right\rangle \,\ne\, 0\). From these properties, one can prove that the optimal measurement vectors \(\left|{\phi }_{i}\right\rangle\) for \({\mathcal{E}}\) can be expressed as

$$\begin{array}{lll}\left|{\phi }_{0}\right\rangle \,=\,\sin \,\chi \left|{F}_{0}\right\rangle -\cos \,\chi \left|{F}_{1}\right\rangle ,\\ \left|{\phi }_{1}\right\rangle \,=\,\frac{1}{\sqrt{2}}(\cos \,\chi \left|{F}_{0}\right\rangle +\sin\, \chi \left|{F}_{1}\right\rangle )+\frac{1}{\sqrt{2}}\left|{F}_{2}\right\rangle ,\\ \left|{\phi }_{2}\right\rangle \,=\,\frac{1}{\sqrt{2}}(\cos \,\chi \left|{F}_{0}\right\rangle +\sin \,\chi \left|{F}_{1}\right\rangle )-\frac{1}{\sqrt{2}}\left|{F}_{2}\right\rangle ,\end{array}$$
(15)

where

$$\begin{array}{lll}\left|{F}_{0}\right\rangle \,=\,\,\cos\,\alpha \left|{E}_{1}\right\rangle +\ \sin\,\alpha \left|{E}_{0}\right\rangle ,\\ \left|{F}_{1}\right\rangle \,=\,\,\ \sin\,\alpha \left|{E}_{1}\right\rangle -\cos\,\alpha \left|{E}_{0}\right\rangle ,\;\left|{F}_{2}\right\rangle =\left|{E}_{2}\right\rangle .\end{array}$$
(16)

Here, we use the optimal measurement’s symmetry, derived from the mirror symmetry of a given ensemble. χ is the value which is determined by applying the necessary condition for the optimal measurement M0(q0ρ0 − q1ρ1)M1 = 0 (in our case, it corresponds to the condition of r〈ϕ0∣ψ0〉〈ψ0∣ϕ1〉 = 〈ϕ0∣ψ1〉〈ψ1∣ϕ1〉)18,19,36) to Eq. (15). It becomes \(\theta \in (\alpha ,\frac{\pi }{2})\), which satisfies the following equation:

$$r\sin\,2\theta ={\sin }^{2}\,\beta \,\sin 2(\theta -\alpha )+\sin 2\beta \,\sin(\theta -\alpha ).$$
(17)

If one substitutes \(\sin (\theta -\alpha )\) into λ, then Eq. (17) is expressed by the following non-trivial fourth-order equation, and χ has a very complex form,

$$\begin{array}{l}4({r}^{2}-2r\cos\,2\alpha\, {\sin }^{2}\,\beta +{\sin }^{4}\,\beta ){\lambda }^{4}+4r\sin\, 2\alpha \,\sin\, 2\beta \ {\lambda }^{3}\\ \qquad-4({r}^{2}-2r\cos\, 2\alpha \,{\sin }^{2}\,\beta -{\sin }^{2}\,\beta \,\cos \,2\beta ){\lambda }^{2}\\ \qquad-2r\sin \,2\alpha \,\sin \,2\beta \ \lambda +{r}^{2}{\sin }^{2}\,2\alpha =0.\end{array}$$

When α, β, and r are given, finding χ is very complicated. However, if χ is given, finding α, β, and r, corresponding to χ, is not difficult. This is because the constraint on r, which is the ratio between the prior probabilities q0 and q1(or q2), requires only positiveness (i.e., 0 < r < ∞). Therefore, when an arbitrary χ is given, if r satisfies the following condition, then (15) are the optimal measurement vectors,

$$r=\frac{{\sin }^{2}\,\beta \,\sin \,2(\chi -\alpha )+\sin\, 2\beta \,\sin (\chi -\alpha )}{\sin\, 2\chi }.$$
(18)

Note that (18) is derived from (17).

Necessary and sufficient condition for global minimum-error probability

Recently, Chitambar and Hsieh provided an important result15. The result states that MD of n nonorthogonal linearly independent pure states can be reduced to the perfect discrimination problem of n orthogonal pure states. Specifically, it was shown that when \({\{{q}_{i},\left|{\psi }_{i}\right\rangle \ \left\langle {\psi }_{i}\right|\}}_{i = 0}^{n-1}\) is a quantum ensemble of n nonorthogonal linearly independent pure states, a measurement provides the guessing probability if and only if the measurement can perfectly discriminate n orthogonal pure states \({\{\left|{\phi }_{i}\right\rangle \ \left\langle {\phi }_{i}\right|\}}_{i = 0}^{n-1}\). Here, \({\{\left|{\phi }_{i}\right\rangle \}}_{i = 0}^{n-1}\) is an orthonormal basis of \({\mathcal{H}}\), where \({\mathcal{H}}\) is the n-dimensional Hilbert space generated by \({\{\left|{\psi }_{i}\right\rangle \}}_{i = 0}^{n-1}\). This basis has the following property: \({\{\left|{\phi }_{i}\right\rangle \ \left\langle {\phi }_{i}\right|\}}_{i = 0}^{n-1}\) is the unique optimal POVM of \({\{{q}_{i},\left|{\psi }_{i}\right\rangle \ \left\langle {\psi }_{i}\right|\}}_{i = 0}^{n-1}\) on \({\mathcal{H}}\). It should be noted that when the space, in which quantum states and measurement operators are defined, is larger than \({\mathcal{H}}\), the minimum-error measurement of \({\{{q}_{i},\left|{\psi }_{i}\right\rangle \ \left\langle {\psi }_{i}\right|\}}_{i = 0}^{n-1}\) is not unique. Therefore, in the case of a multi-party system, the global minimum-error probability of \({\{{q}_{i},\left|{\psi }_{i}\right\rangle \ \left\langle {\psi }_{i}\right|\}}_{i = 0}^{n-1}\) can be achieved by finite-round (asymptotic) LOCC if and only if \({\{\left|{\phi }_{i}\right\rangle \ \left\langle {\phi }_{i}\right|\}}_{i = 0}^{n-1}\) can be perfectly discriminated using the finite-round (asymptotic) LOCC.

Perfect discrimination of quantum states by SEPs

Duan et al.11 tells that in a two-qubit system, when \(\{\left|{{{\Xi }}}_{0}\right\rangle ,\left|{{{\Xi }}}_{1}\right\rangle ,\left|{{{\Xi }}}_{2}\right\rangle ,\left|{{\Gamma }}\right\rangle \}\) is an orthonormal basis, the necessary and sufficient condition for \({\{\left|{{{\Xi }}}_{i}\right\rangle \ \left\langle {{{\Xi }}}_{i}\right|\}}_{i = 0}^{2}\) to be distinguished by a SEP is as follows: (i) ΞkΓ−1 has two antiparallel eigenvalues for each entangled \(\left|{{{\Xi }}}_{k}\right\rangle\) and (ii) \(\mathop{\sum }\nolimits_{i = 0}^{2}C({{{\Xi }}}_{i})=C({{\Gamma }})\), where Ψ corresponding to \(\left|{{\Psi }}\right\rangle\) is a 2 × 2 matrix satisfying \(\left|{{\Psi }}\right\rangle =(I\otimes {{\Psi }})\left|{{{\Phi }}}_{\frac{\pi }{4}}^{+}\right\rangle\) and C(Ψ) denotes the concurrence of \(\left|{{\Psi }}\right\rangle\), i.e., \(C({{\Psi }})=| \det\,{{\Psi }}|\). In particular, when \(\left|{{\Gamma }}\right\rangle\) is maximally entangled, \({\{\left|{{{\Xi }}}_{i}\right\rangle \ \left\langle {{{\Xi }}}_{i}\right|\}}_{i = 0}^{2}\) can be perfectly discriminated by an SEP if and only if \(\mathop{\sum }\nolimits_{i = 0}^{2}C({{{\Xi }}}_{i})=1\).