Direct estimation of quantum coherence by collective measurements

Abstract

The recently established resource theory of quantum coherence allows for a quantitative understanding of the superposition principle, with applications reaching from quantum computing to quantum biology. While different quantifiers of coherence have been proposed in the literature, their efficient estimation in today’s experiments remains a challenge. Here, we introduce a collective measurement scheme for estimating the amount of coherence in quantum states, which requires entangled measurements on two copies of the state. As we show by numerical simulations, our scheme outperforms other estimation methods based on tomography or adaptive measurements, leading to a higher precision in a large parameter range for estimating established coherence quantifiers of qubit and qutrit states. We show that our method is accessible with today’s technology by implementing it experimentally with photons, finding a good agreement between experiment and theory.

Introduction

Quantum coherence is the most distinguished feature of quantum mechanics, characterizing the superposition properties of quantum states. An operational resource theory of coherence has been established in the last years^{1,2,3,4,5,6,7}, allowing for a systematic study of quantum coherence in quantum technology⁶, including quantum algorithms^8,9, quantum computation¹⁰, quantum key distribution¹¹, quantum channel discrimination^12,13, and quantum metrology^14,15,16. Moreover, quantum coherence is closely related to other quantum resources, such as asymmetry^17,18, entanglement^19,20, and other quantum correlations²¹; the manipulation of coherence and conversion between coherence and quantum correlations in bipartite and multipartite systems has been explored both theoretically^22,23,24,25 and experimentally^26,27. Highly relevant from the experimental perspective is the recent progress on coherence theory in the finite copy regime, in particular regarding single-shot coherence distillation^28,29,30,31, coherence dilution³², and incoherent state conversion³³. Being a fundamental property of quantum systems, coherence plays an important role in quantum thermodynamics^{34,35,36,37,38,39,40}, nanoscale physics⁴¹, transport theory^42,43, biological systems^{44,45,46,47,48,49}, and for the study of the wave-particle duality^50,51,52.

Having identified quantum coherence as a valuable feature of quantum systems, it is important to develop methods for its rigorous quantification. First attempts for resource quantification were made in the resource theory of entanglement^53,54, leading to various entanglement measures based on physical or mathematical considerations. The common feature of all resource quantifiers is the postulate that they should not increase under free operations of the theory, which in entanglement theory are known as “local operations and classical communication”. In the resource theory of coherence, the free operations are incoherent operations, corresponding to quantum measurements, which cannot create coherence for individual measurement outcomes¹.

While various coherence measures have been proposed⁶, an important issue is how to efficiently estimate them in experiments. Clearly, one possibility is to perform quantum state tomography⁵⁵ and then use the derived state density matrix to estimate the amount of coherence. However, estimation of coherence measures in general does not require the complete information about the state of the system, a fact which has been exploited in various approaches for detecting and estimating coherence of unknown quantum states^56,57,58,59.

In this paper, we put forward a general method to directly measure quantum coherence of an unknown quantum state using two-copy collective measurement scheme (CMS)^60,61,62,63. We simulate the performance of this method for qubits and qutrits and compare the precision of CMS with other methods for coherence estimation, including tomography. The simulations show that in certain setups CMS outperforms all other schemes discussed in this work. We also report an experimental demonstration of CMS for qubit states. The collective measurements are performed on two identically prepared qubits, which are encoded in two degrees of freedom of a single photon. In this way, we experimentally obtain two widely studied coherence measures, finding a good agreement between the numerical simulations and the experimental results.

Results

Theoretical framework

We aim to estimate coherence of a quantum state ρ by performing measurements on two copies of the state. As quantifiers of coherence we use the ℓ₁-norm of coherence ${C}_{{\ell }_{1}}$ and the relative entropy of coherence C_r, defined as¹:

$${C}_{{\ell }_{1}}(\rho )={\sum\limits _{i\ne j}}\left|{\rho }_{ij}\right|,$$

(1)

$${C}_{r}(\rho )=S({\rho }_{{\mathrm{diag}}})-S(\rho ).$$

(2)

Here, $S(\rho )=-{\rm{Tr}}[\rho \,{\mathrm{log}\,}_{2}\rho ]$ is the von Neumann entropy, ${\rho }_{{\mathrm{diag}}}={\sum }_{i}\left|i\right\rangle \left\langle i\right|\rho \left|i\right\rangle \left\langle i\right|$, and we consider coherence with respect to the computational basis $\{\left|i\right\rangle \}$. For single-qubit states with Bloch vector r = (r_x, r_y, r_z), both quantities can be expressed as⁶⁴:

$${C}_{{\ell }_{1}}(\rho )=\sqrt{{r}_{x}^{2}+{r}_{y}^{2}},$$

(3)

$${C}_{r}(\rho )=h\left(\frac{1+\left|{r}_{z}\right|}{2}\right)-h\left(\frac{1+r}{2}\right)$$

(4)

with the binary entropy $h(x)=-x\,{\mathrm{log}\,}_{2}x-(1-x)\,{\mathrm{log}\,}_{2}(1-x)$ and the Bloch vector length $r={({r}_{x}^{2}+{r}_{y}^{2}+{r}_{z}^{2})}^{1/2}$.

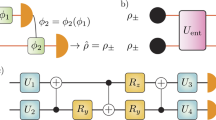
In the next step, we will express both ${C}_{{\ell }_{1}}$ and C_r in terms of the outcome probabilities of a collective measurement in the maximally entangled basis, performed on two copies ρ ⊗ ρ. We denote the corresponding outcome probabilities as ${P}_{i}={\rm{Tr}}[{M}_{i}\rho \otimes \rho ]$, where

$$\begin{array}{ll}{M}_{1}=\left|{\psi }^{+}\right\rangle \ \left\langle {\psi }^{+}\right|,\ \ \ \ \ {M}_{2}=\left|{\psi }^{-}\right\rangle \ \left\langle {\psi }^{-}\right|,\\ {M}_{3}=\left|{\varphi }^{+}\right\rangle \ \left\langle {\varphi }^{+}\right|,\ \ \ \ \ {M}_{4}=\left|{\varphi }^{-}\right\rangle \ \left\langle {\varphi }^{-}\right|\end{array}$$

(5)

are projectors onto maximally entangled states $\left|{\psi }^{\pm }\right\rangle =(\left|01\right\rangle \pm \left|10\right\rangle )/\sqrt{2}$ and $\left|{\varphi }^{\pm }\right\rangle =(\left|00\right\rangle \pm \left|11\right\rangle )/\sqrt{2}$. As we show in Method section, the outcome probabilities fulfill the relations

$$\begin{array}{ll}{r}_{x}^{2}+{r}_{y}^{2}=2({P}_{1}-{P}_{2}),\\ | {r}_{z}| =\sqrt{2\left({P}_{3}+{P}_{4}\right)-1},\\ r=\sqrt{1-4{P}_{2}}.\end{array}$$

(6)

Thus, both coherence measures ${C}_{{\ell }_{1}}$ and C_r can be expressed as simple functions of P_i. We further note that in general CMS can be used to estimate absolute values of the Bloch vector components of a single-qubit state ρ. This implies that CMS allows to evaluate any coherence measure of single-qubit states, as any such measure is a function of the absolute values of the Bloch coordinates, see Method section for more details.

In the following, we use numerical simulation to compare the collective measurement scheme (CMS) discussed above to three alternative schemes for measuring ${C}_{{\ell }_{1}}$ for single-qubit states. The first alternative scheme is to directly measure observables σ_x and σ_y, and estimate ${C}_{{\ell }_{1}}$ via Eq. (3). The second scheme is a two-step adaptive measurement: step one is to measure observables σ_x and σ_y; based on the feedback results of the first step, step two is to choose optimal observable aσ_x + bσ_y to obtain $| \langle 0| \rho | 1\rangle |$. The third alternative scheme is to perform state tomography and then, subject to the derived density matrix, to estimate the value of ${C}_{{\ell }_{1}}$. We further use the tomography results to estimate the relative entropy of coherence C_r via Eq. (4), and compare the performance of the estimation with CMS.

For the numerical simulation we use single-qubit states

$$\left|\Psi \right\rangle =\sin \theta \left|0\right\rangle +\cos \theta \left|1\right\rangle$$

(7)

with θ ranging from 0 to π/2. All simulations are performed on N = 1200 copies of $\left|\Psi \right\rangle$. We further repeat each simulation 1000 times and average the numerical data overall repetitions. We are in particular interested in the error of the estimation:

$$\varepsilon =\left|{C}_{{\rm{est}}}(\rho )-C(\rho )\right|,$$

(8)

where C_est and C are the estimated and the actual coherence measures, respectively. Figure 1a shows the results of numerical simulation for ${C}_{{\ell }_{1}}$, together with experimental data; the experiment will be discussed in more detail below. Each data point in the figure is the average of T = 1000 repetitions, i.e., $\frac{1}{T}\mathop{\sum }\nolimits_{i = 1}^{T}{\varepsilon }_{i}$, where ε_i is the error of the ith measurement. The error bar denotes the standard deviation of ε_i. Figure 1b shows the corresponding comparison between CMS and tomography for estimating the relative entropy of coherence C_r.

Fig. 1: Results of estimation error for qubit.

Mean errors for estimating ℓ₁-norm coherence in a and relative entropy coherence in b for a family of qubit states with different measurement schemes. The states have the form $\left|\Psi \right\rangle =\sin \theta \left|0\right\rangle +\cos \theta \left|1\right\rangle$ with θ ranging from 0 to π/2. In a, the performances of CMS (numerical simulation and experiment); σ_x, σ_y measurement (simulation); two-step adaptive measurements (simulation); and tomography (simulation) are shown for comparison. In b, the performances of CMS (numerical simulation and experiment) and tomography (simulation) are shown for comparison. The sample size is N = 1200. Each data point is the average of 1000 repetitions, and the error bar denotes the standard deviation.

As we see from the data shown in Fig. 1a, b, there is a range of θ where CMS outperforms all other schemes, leading to the smallest error. Moreover, while the error in general depends on θ, this dependence is comparably weak for CMS. To compare the accuracy achieved by different estimation methods more intuitively and clearly, we average the mean error for all input states shown in Fig. 1a, and the average results are shown in Fig. 2. For the estimation of ${C}_{{\ell }_{1}}$ the adaptive measurement scheme outperforms CMS on average, which again outperforms all other estimation schemes presented above. In the Supplementary Information we further report theoretical and experimental results for estimating coherence of formation^3,65 for qubits. Also in this case CMS outperforms all other schemes discussed in this paper in a certain range of θ.

Fig. 2: Average results of estimation error for qubit.

Average results of the mean error for all input states shown in Fig. 1a. The corresponding average values of these methods from left to right: 0.0263, 0.0234, 0.0156, 0.0176, 0.0187.

While the above discussion was restricted to qubit systems, the CMS method can also be applied to estimate ${C}_{{\ell }_{1}}$ for states of higher dimensions. We consider an arbitrary quantum state $\rho ={\sum }_{i,j}{\rho }_{ij}\left|i\right\rangle \left\langle j\right|$, where i, j = 0, 1, …, d − 1 and d is the dimension of Hilbert space. After an appropriate set of collective measurements are performed on the two-copy state ρ ⊗ ρ, we find that the absolute value of the off-diagonal element ∣ρ_ij∣ for i ≠ j can be expressed as

$$|{\rho }_{ij}|=\sqrt{\frac{1}{2}({\rm{Tr}}[{\rho }^{\otimes 2}|{\psi }_{ij}^{+}\rangle \ \langle {\psi }_{ij}^{+}|]-{\rm{Tr}}[{\rho }^{\otimes 2}|{\psi }_{ij}^{-}\rangle \ \langle {\psi }_{ij}^{-}|])},$$

(9)

where $|{\psi }_{ij}^{\pm }\rangle =(\left|ij\right\rangle \pm \left|ji\right\rangle )/\sqrt{2}$. Therefore, the ℓ₁-norm coherence can be written as

$${C}_{{\ell }_{1}}(\rho )=2\sum _{j\,>\,i}\sqrt{\frac{1}{2}({\rm{Tr}}[{\rho }^{\otimes 2}|{\psi }_{ij}^+\rangle \ \langle {\psi }_{ij}^+|]-{\rm{Tr}}[{\rho }^{\otimes 2}|{\psi }_{ij}^-\rangle \ \langle {\psi }_{ij}^-|])}.$$

(10)

We use numerical simulation to compare the performance of the CMS method to the qutrit state tomography for the family of qutrit states

$$\left|\Phi \right\rangle =\frac{1}{\sqrt{2}}(\sin \alpha \left|0\right\rangle +\cos \alpha \left|1\right\rangle +\left|2\right\rangle ),$$

(11)

with α ranging from 0 to π/2 (see Supplementary Information for more details). The results of the simulation are shown in Fig. 3. As before, we use N = 1200 copies of the state $\left|\Phi \right\rangle$ for both CMS and state tomography, and average over 1000 repetitions. The results show that CMS outperforms the tomography method for a large range of α. Apart from a higher accuracy, the CMS method requires only a single measurement setup, while four measurement setups are required for qutrit tomography.

Fig. 3: Results of estimation error for qutrit.

Mean error for estimating ${C}_{{\ell }_{1}}$ for a family of qutrit states in Eq. (11) for CMS and qutrit state tomography (numerical simulation). The sample size is N = 1200. Each data point is the average of 1000 repetitions, and the error bars denote the standard deviation.

Experimental implementation

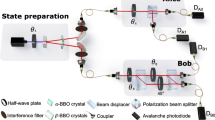
The experimental setup for realizing CMS to estimate coherence of qubit states is presented in Fig. 4. The setup is composed of three modules designed for single-photon source, two-copy state preparation, and collective measurements, respectively. In the single-photon source module, a 80-mW cw laser with a 404-nm wavelength (linewidth = 5 MHz) pumps a type-II beamlike phase-matching beta-barium-borate (BBO, 6.0 × 6.0 × 2.0 mm³, θ = 40.98^∘) crystal to produce a pair of photons with wavelength λ = 808 nm. The two photons pass through two interference filters (IF) whose FWHM (full width at half maximum) is 3 nm. The photon pairs generated in spontaneous parametric down-conversion (SPDC) are coupled into single-mode fibers separately. One photon is detected by a single-photon detector acting as a trigger. The coincidence counts are ~5 × 10³ per second. In the two-copy state preparation module, we first prepare copy 1 in the path degree of freedom of single photon, i.e., the first qubit encoded in positions 1 and 0 (see a in Fig. 4). After passing a half-wave plate (HWP) and a quarter-wave plate (QWP) with deviation angles H₁, Q₁, the photon is prepared in the desired state ρ. To encode the polarization state into the path degree of freedom, beam displacer (BD₁) is used to displace the horizontal polarization (H) component into path 0, which is 4-mm away from the vertical polarization (V) component in path 1; then a HWP (H₃) with deviation angle 45^∘ is placed in path 0. The resulting photon is described by the state $\rho \otimes \left|V\right\rangle \left\langle V\right|$. Then we encode the second copy of ρ into the polarization degree of freedom of single photon using a HWP and a QWP with deviation angles H₂, Q₂ (see b in Fig. 4). In this way, we can prepare the desired two-copy state ρ ⊗ ρ.

Fig. 4: Experimental setup for measuring coherence of qubit with collective measurements.

The setup consists of three modules designed for single-photon source, two-copy state preparation (a, b) and collective measurement, respectively. In the single-photon source module, the photon pairs generated in spontaneous parametric down-conversion are coupled into single-mode fibers separately. One photon is detected by a single-photon detector (SPD) acting as a trigger. In the two-copy state preparation module, a prepares the first copy in the path degree of freedom of the photon; b prepares the second copy in the polarization degree of freedom of the photon. In the collective measurement module, combinations of beam displacers (BDs) and half-wave plates (HWPs) with certain angular settings are used to realize collective measurement, where H₄ and H₅ are 22.5^∘. Four SPDs M₁ to M₄ correspond to the four outcomes of the collective measurement. Each SPD is a silicon avalanche photodiode (Si-APD), with detection efficiency of ~60%.

The collective measurement module realizes a measurement on ρ ⊗ ρ in the maximally entangled basis, where M_i are given in Eq. (5). When estimating the ℓ₁-norm coherence, only the probabilities of the outcomes M₁ and M₂ are used, see the discussion below Eq. (3). The probabilities of all outcomes are used for estimating the relative entropy of coherence, see Eq. (4). To verify the experimental implementation of the collective measurement, we take the conventional method of measuring the probability distributions after preparing the input states $\left|{\psi }^{+}\right\rangle$, $\left|{\psi }^{-}\right\rangle$, $\left|{\varphi }^{+}\right\rangle$ and $\left|{\varphi }^{-}\right\rangle$. These input states can be prepared by choosing proper rotation angles H₁, Q₁, H₂, H₃ as specified in the Supplementary Information. Each input state is prepared and measured 5000 times, and the probability of obtaining the outcomes M₁, M₂, M₃, and M₄ are 0.9981 ± 0.0006, 0.9973 ± 0.0007, 0.9962 ± 0.0009, and 0.9961 ± 0.0009, respectively (ideal value is 1). The theoretical values of other probability distributions for the input states are all 0, experimentally the maximum error of other probability is 0.0037 ± 0.0009.

The experimental deterministic realization of the collective measurement allows us to estimate the amount of coherence with a single measurement setup. We experimentally investigate the error achieved by CMS when the input states $\left|\Psi \right\rangle$ have the form Eq. (7) with θ ranging from 0 to π/2. The sample size of the experiment is N = 1200 copies of $\left|\Psi \right\rangle$; same sample size has been used in the numerical simulations reported above. As in the numerical simulation, we average over 1000 repetitions of the experiment. The experimental results for the estimation precision of ${C}_{{\ell }_{1}}$ and C_r are shown in Fig. 1a, b, respectively. The experimental data are in good agreement with the theoretical prediction. The errors in our experiment mainly come from the inaccuracy of angles of the wave plates and the imperfect interference visibility of the interferometer.

Discussion

We introduce a general method to directly measure quantum coherence of an unknown quantum state using two-copy collective measurement, focusing on two established coherence quantifiers: ℓ₁-norm coherence and relative entropy coherence. As we demonstrate by numerical simulation for qubit and qutrit states, in a certain parameter region the collective measurement scheme outperforms other estimation techniques, including methods based on adaptive σ_x, σ_y measurement for qubits, and tomography-based coherence estimation for qubits and qutrits. We test our results by experimentally estimating the ℓ₁-norm coherence and relative entropy coherence of qubit states by collective measurements in optical setup, finding good agreement between theory and experiment. For single-qubit states our method allows to estimate absolute values of the Bloch coordinates, implying that any coherence quantifier of a qubit can be estimated with the collective measurement scheme.

Although the precision achieved by our method is not always better than by adaptive measurement, our scheme has several advantages with respect to other techniques. In particular, our method does not need any optimization procedures or feedback, which are required for coherence estimation via adaptive measurements. Moreover, the entire experiment can be performed in a single measurement setup. Thus, our work provides a simple method to measure coherence, and highlights the application of collective measurement in quantum information processing.

Methods

Estimating general coherence measures for qubits with collective measurements

For a single-qubit state ρ with Bloch vector r = (r_x, r_y, r_z) the probabilities ${P}_{i}={\rm{Tr}}[{M}_{i}\rho \otimes \rho ]$ are given explicitly as

$$\begin{array}{ll}{P}_{1}=\left\langle {\psi }^+| \rho \otimes \rho | {\psi }^{+}\right\rangle =\frac{1}{4}(1+{r}_{x}^{2}+{r}_{y}^{2}-{r}_{z}^{2}),\\ {P}_{2}=\left\langle {\psi }^-| \rho \otimes \rho | {\psi }^-\right\rangle =\frac{1}{4}(1-{r}_{x}^{2}-{r}_{y}^{2}-{r}_{z}^{2}),\\ {P}_{3}=\left\langle {\varphi }^+| \rho \otimes \rho | {\varphi}^+\right\rangle =\frac{1}{4}(1+{r}_{x}^{2}-{r}_{y}^{2}+{r}_{z}^{2}),\\ {P}_{4}=\left\langle {\varphi }^-| \rho \otimes \rho | {\varphi }^-\right\rangle =\frac{1}{4}(1-{r}_{x}^{2}+{r}_{y}^{2}+{r}_{z}^{2}).\end{array}$$

(12)

It thus follows that collective measurements can be used to evaluate absolute values of the Bloch coordinates:

$$\begin{array}{ll}\left|{r}_{x}\right|=\sqrt{2\left({P}_{1}+{P}_{3}\right)-1},\\ \left|{r}_{y}\right|=\sqrt{2\left({P}_{1}+{P}_{4}\right)-1},\\ \left|{r}_{z}\right|=\sqrt{2\left({P}_{3}+{P}_{4}\right)-1}.\end{array}$$

(13)

From these results, it is straightforward to verify Eq. (6).

In the following, C(r_x, r_y, r_z) will denote a coherence measure for a qubit state ρ with Bloch vector r = (r_x, r_y, r_z). As we will now show, for single-qubit states any coherence measure C depends only on the absolute values of the Bloch vector coordinates. For this, it is enough to show that

$$C({r}_{x},{r}_{y},{r}_{z})=C(-{r}_{x},{r}_{y},{r}_{z})=C({r}_{x},-{r}_{y},{r}_{z})=C({r}_{x},{r}_{y},-{r}_{z})$$

(14)

for any coherence measure C and any Bloch vector. This can be seen by noting that the vector (r_x, r_y, r_z) can be transformed into the vector (−r_x, r_y, r_z) via a rotation around the z-axis, which corresponds to an incoherent unitary operation. Since any coherence measure is invariant under incoherent unitaries, it follows that C(r_x, r_y, r_z) = C(−r_x, r_y, r_z). By similar arguments we obtain C(r_x, r_y, r_z) = C(r_x, −r_y, r_z). Moreover, note that σ_x is an incoherent unitary inducing the transformation (r_x, r_y, r_z) → (r_x, −r_y, −r_z), and thus it must be that C(r_x, r_y, r_z) = C(r_x, −r_y, −r_z). Combining these arguments completes the proof of Eq. (14).